A technique for production scheduling problems is a methodology that optimizes the use of available resources by ordering a sequence of operations of jobs assigned to each resource. The scheduling problems are computationally very complex and therefore it is difficult to optimally solve in a reasonable time due to the combinatorial nature of its solution. As a result, finding a near-optimal solution in a reasonable time is important in real manufacturing area.
In a parallel machine scheduling problem, a set of the independent jobs are processed on a number of available identical parallel machines. Each machine processes only one job at a time, and each job can be processed on one of any machines with same processing time. But, in a non-identical parallel machine scheduling problem, the processing times of jobs depend upon the machine to which they are assigned to. Furthermore, the consideration of setup times between jobs is dependent upon not only the sequence of jobs to be processed on a machine but also the machine to which the jobs are assigned. In other words, the setup time between job
Solving scheduling problems with sequence-dependent setup times is a very active research area (Allahverdi
For identical parallel machine problems, Monma and Potts (1989) considered the complex computing of scheduling parallel machine with sequence-dependent setup cost in batch processing machines. Tahar
Driessel and Monch (2010) addressed a parallel machine scheduling problem to minimize total weighted tardiness with sequence-dependent setup times, precedence constraints and ready time and proposed variable neighborhood search (VNS) heuristic to solve the problem.
For non-identical parallel machine scheduling problems, several studies have found. Agarwal
Motivated by the literature discussed above, this paper considers the non-identical parallel machine scheduling problem with sequence and machine dependent setup times to minimize makespan. Though the problem can be formulated to a mathematical model, the model is not tractable as the problem size become large. Therefore, two meta-heuristic approaches are designed to solve the problem in a reasonable time. In section 2, a mathematical model is derived for finding the optimal solution. Two meta-heuristic algorithms, genetic algorithm (GA) and a new population-based evolutionary meta-heuristic called self-evolution algorithm (SEA), are proposed in section 3. In section 4, the performances of the metaheuristics are evaluated through computational experiments. Finally, summary and further research areas are remarked in section 5.
In this section, we propose a mixed integer programming model for a non-identical parallel machine scheduling problem with sequence and machine dependent setup times scheduling problem to minimize makespan. The following notations are used:
pik : processing time of job i on machine k.
sijk : sequence and machine dependent setup time of job j processed after job i on machine k.
sOik : setup time of job i if job i is the first job in job sequence on machine k.
MS : set of machines
JS : set of jobs to be scheduled
O : dummy job index
M : big number
xi : starting time of job i
cmax : makespan
The mathematical model is as given below:
xi ≥ 0, for ∀i ∈ JS,
yik = 0 or 1, for ∀i ∈ JS, ∀k ∈ MS,
zijk = 0 or 1, for ∀i ∈ JS, ∀k ∈ MS,
zoik = 0 or 1, for ∀i ∈ JS, ∀k ∈ MS,
In this model, a dummy job notation
The mixed integer programming model is not tractable for the problems over total 12 jobs because of the computation time (See Section 4). Thus, we focus on developing effective meta-heuristic approaches instead. In identical parallel machine scheduling problems with sequence dependent setup times, several authors have reported the effectiveness of the meta-heuristic approaches. Mendes
In this paper, we propose two meta-heuristics as solution approach for the non-identical parallel machine scheduling problem; conventional genetic algorithm (GA) and self-evolution algorithm (SEA) using one dimensional representation with special character. SEA is a new population-based evolutionary meta-heuristic. GA is one of the most powerful and broadly applicable metaheuristic based on principles from evolution theory. GA was first introduced and investigated by Holland (1975), and known as an effective and efficient algorithm for combinatorial optimization problems (Gen and Cheng, 2000). In general, the solution representation (chromosome) with a special character for separating machines has been used to apply GA in parallel machine scheduling problems (Cheng and Gen, 1997; Tavakkoli-Moghaddam
3.1 Representation of Solutions
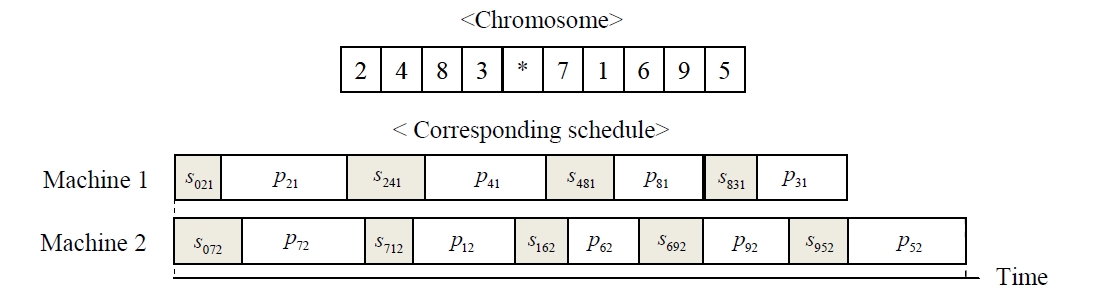
In meta-heuristics, the solution performance is highly dependent upon the representation of a solution. For both meta-heuristic GA and SEA, it is necessary to describe the representation of a solution for the corresponding non-identical parallel machine schedule, and the representation is called
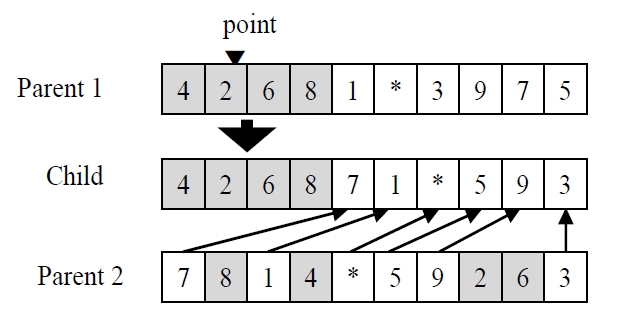
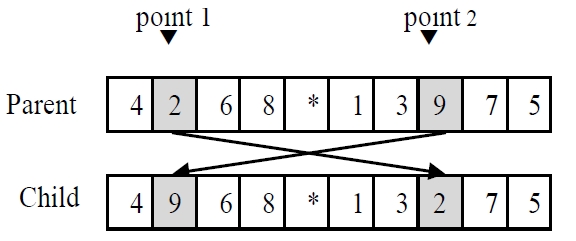
In the GA using chromosomes with special character, every chromosome is encoded into a structure that represents its properties, and the set of chromosomes forms a population. Initial population is generated randomly for the first generation. The chromosomes in the population are evaluated using the makespan of nonidentical parallel machines as the measure of fitness. The chromosomes that have higher fitness value (lower objective function value) than the average fitness of current population make a potential parent pool. Parents are randomly selected only in the potential parent pool. Using three genetic operators such as a crossover operator, a mutation operator and a reproduction operator, the selected parents reproduce new chromosomes (i.e., children) to generate a population for the next generation. One-point crossover is used for both GA, and the crossover is illustrated in Figure 2. One point is randomly selected for dividing one parent. The set of genes on left side is inherited from the parent to the child, and the other genes are placed in order of their appearance in the other parent. For the mutation, two genes of a parent randomly selected are interchanged in GA as shown in
Figure 3 (swap mutation). So a new generation is probabilistically formed according to the fitness values of chromosomes by genetic operators. Then the generation is evaluated and this process is repeated until a stopping criterion (maximum number of generations) is met.
3.3 Self-Evolution Algorithm (SEA)
SEA is a new meta-heuristic algorithm which has a population (a set of solutions) based mechanism using the evolution of a solution by itself (self-evolution). Similar to GA, the set of chromosomes forms a population. The chromosome with special character proposed in Section 3.1 is also used for SEA. Initial population is generated randomly, and the chromosomes in the population are evaluated using the makespan of the nonidentical parallel machines as the measure of fitness. A chromosome from the population is randomly selected and executes a self-reproduction using a randomly selected evolution operator to make a new chromosome. Then the new chromosome is evaluated and it replaces the original chromosome, if the fitness value of the new chromosome is better than that of the original chromosome. The algorithm continues until the number of selfreproductions becomes a predetermined stopping value.
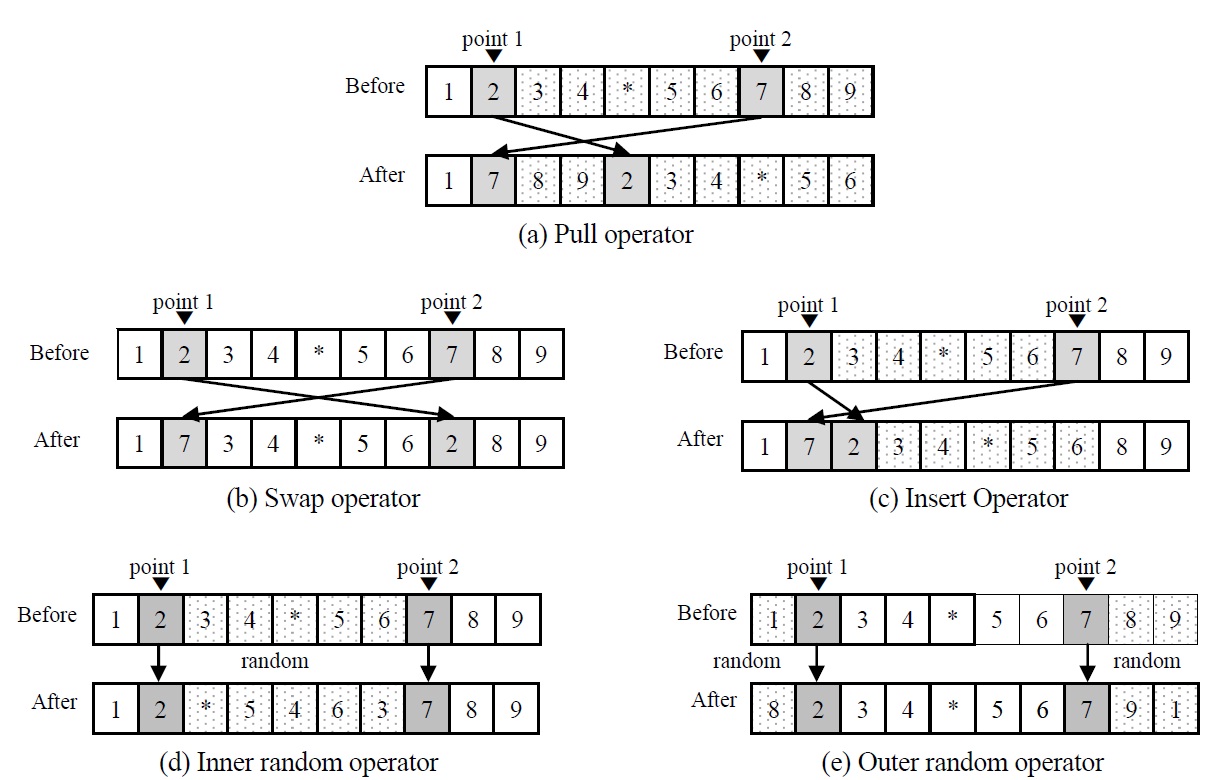
We propose five evolution operators (pull operator, insert operator, swap operator, inner random operator and outer random operator) to make a new chromosome. For the operators, two points in the selected original chromosome are randomly selected. The pull operator is illustrated in Figure 4(a). The genes on right side of
point 2 (including point 2) are pulled to the position of point 1, and the genes between point 1 and 2 (including point 1) are placed after. The two genes at the points are interchanged for swap operator as shown in Figure 4(b). Insert operator simply insert the gene at point 2 into the position of point 1 as shown in Figure 4(c). Inner random operator and outer random operator are illustrated in Figure 4(d) and Figure 4(e). The inner or outer genes of point 1 and 2 are randomly replaced for the operators.
SEA is running without providing any parameters for the algorithm, because all the selection processes in SEA, such as selection of chromosome from the population for self-evolution, selection of evolution operator, and selection of points for the operator are randomly executed.
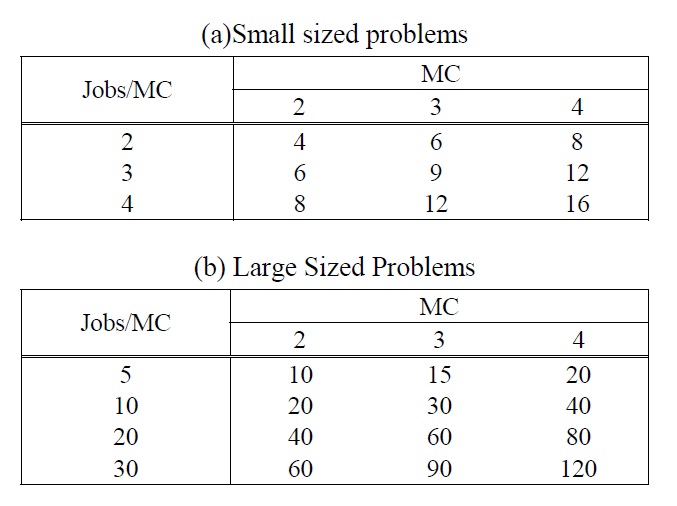
To evaluate the performances of the meta-heuristic algorithms proposed in this paper, computational experiments were conducted using randomly generated test problems. Since the complexity of a problem highly depends on the number of jobs per machine, we fixed the number of machines as 2, 3, and 4 and generated two problem groups according to the average job size per machine. Total job size of each problem group is summarized in Table 1. The processing time and sequence and machine dependent setup time were randomly generated according to the range of [60, 180] and [10, 60], respectively, and the initial setup time was randomly generated by one value in the 70% range of the setup time.
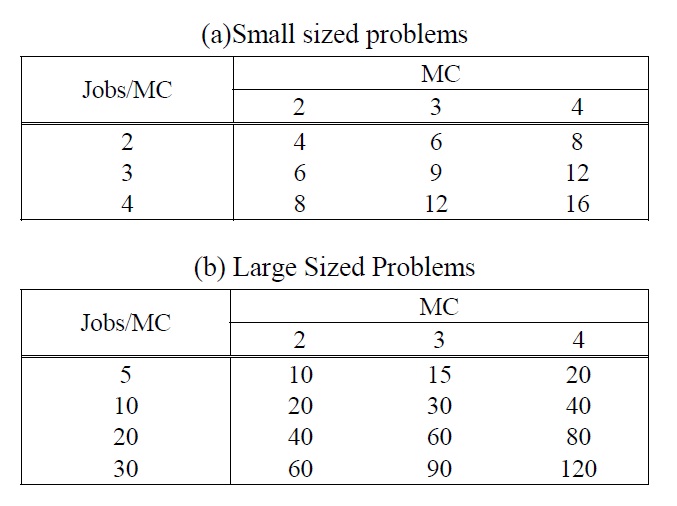
Total Job Size.
The small sized problems in the first group were generated for comparing the solutions obtained by meta-
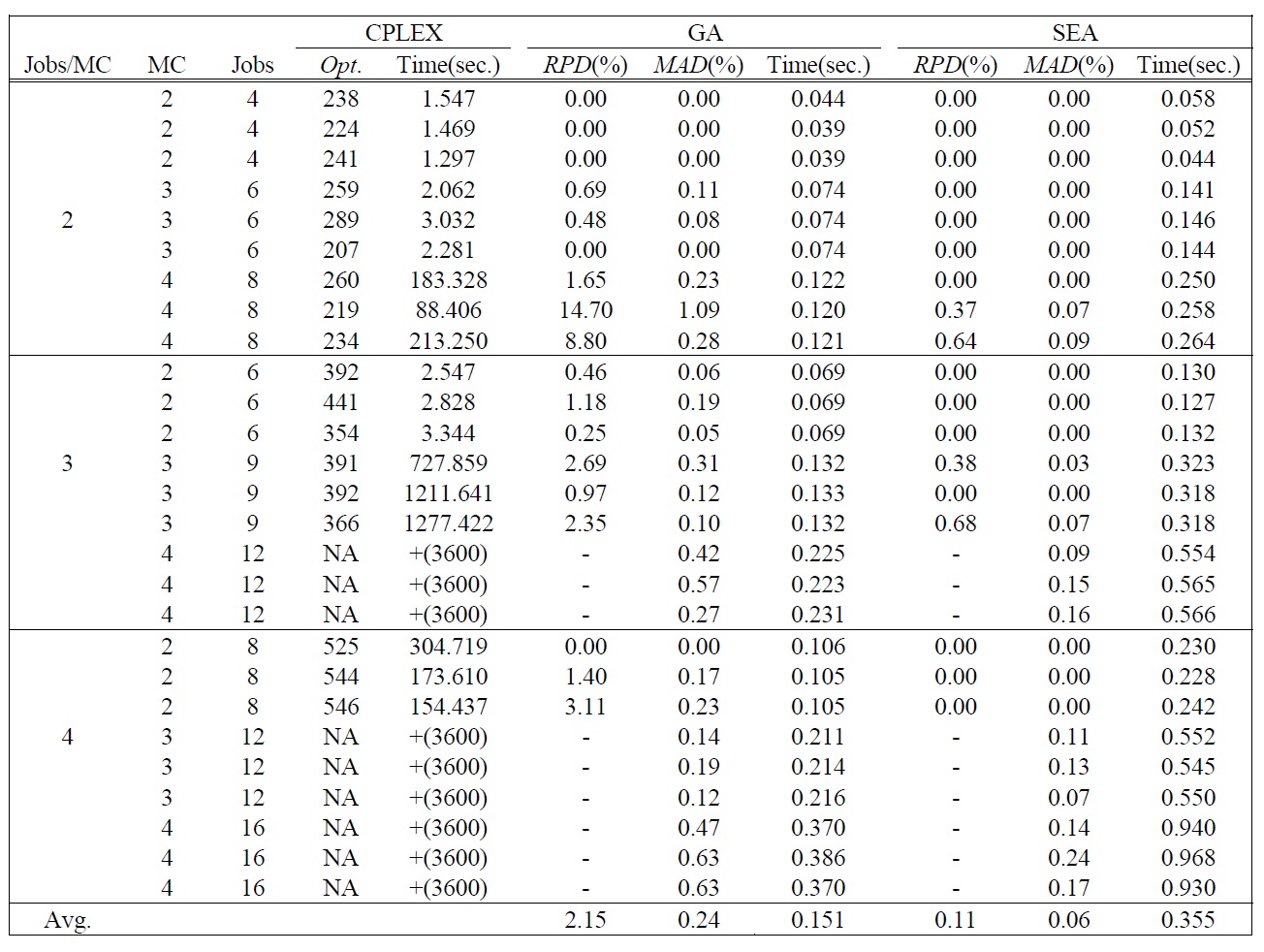
[Table 2.] Test Results of Small Sized Problems.
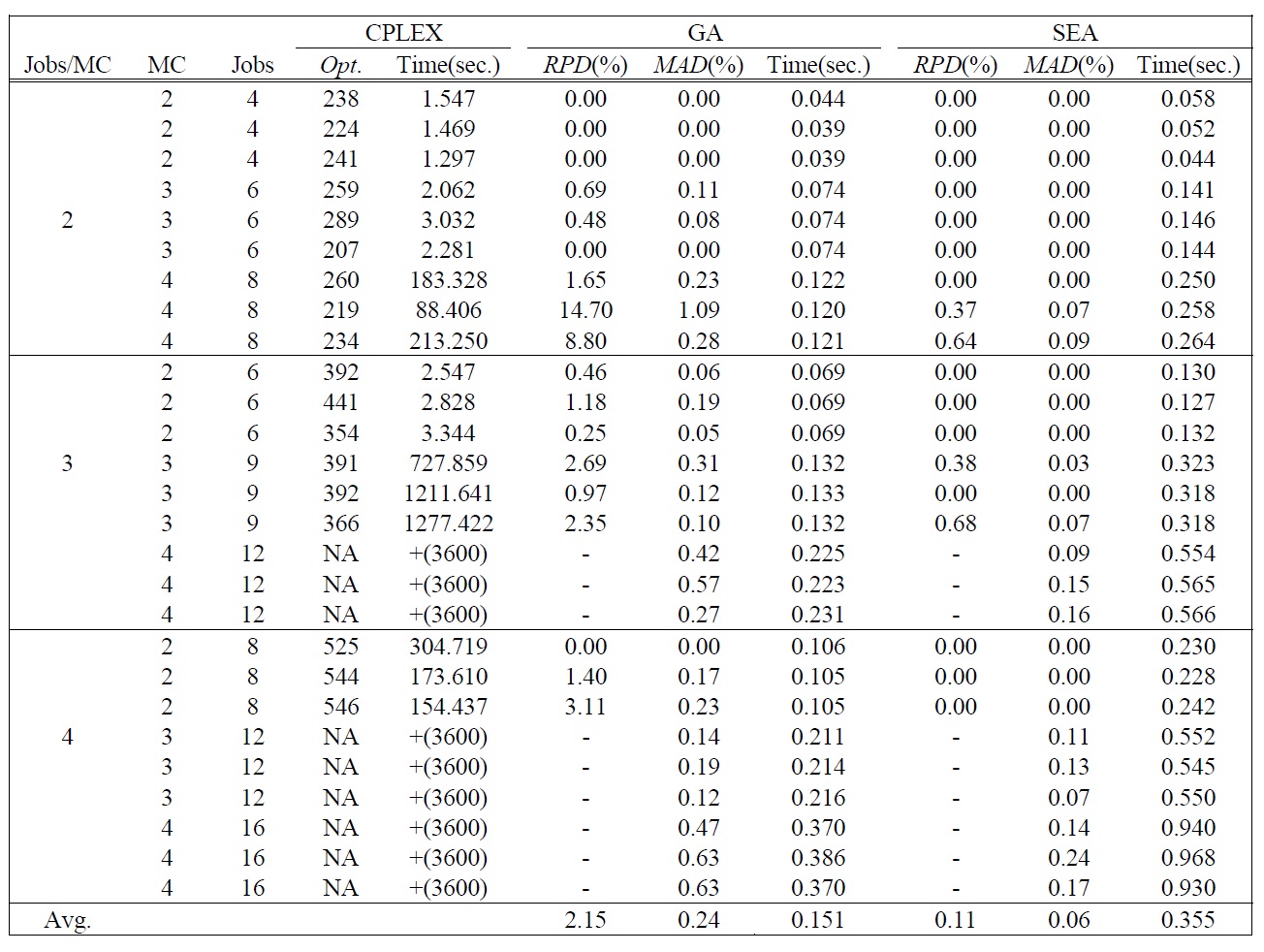
Test Results of Small Sized Problems.
heuristic algorithms with optimal solutions. We used ILOG CPLEX 10.2 for finding the optimal solutions with the mathematical model presented in section 2. We imposed a 3600(sec.) time limit and simply terminated a particular run if the optimal solution had not been found and verified in that amount of time. The second group is to compare the performance of each meta-heuristic algorithm with large sized problems. GA was running with a population size of 2 ?
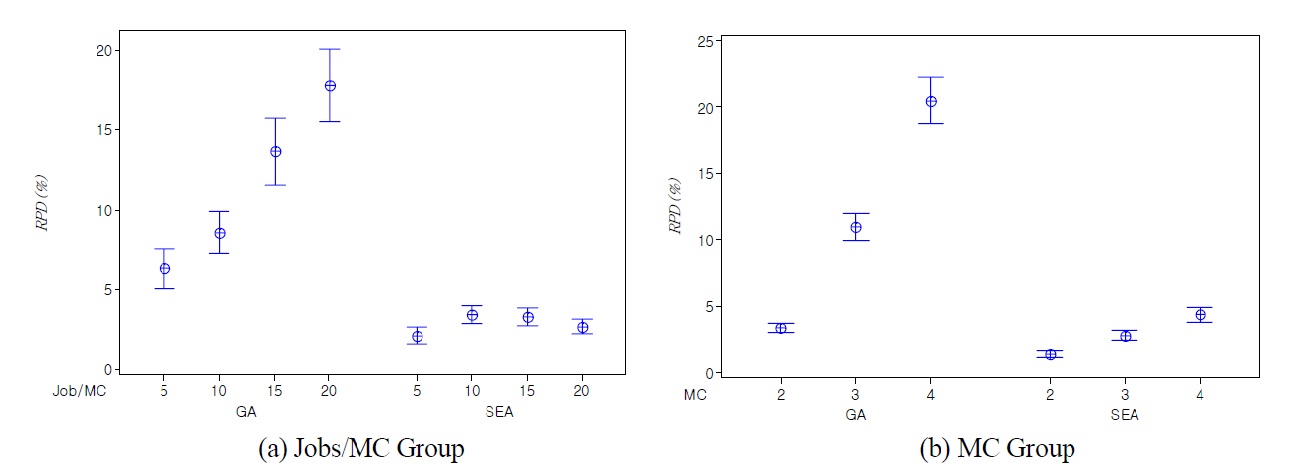
The test results of small sized problems are summarized in Table 2. Table 2 shows the optimal solution by CPLEX and mean and mean absolute deviation (
where
The
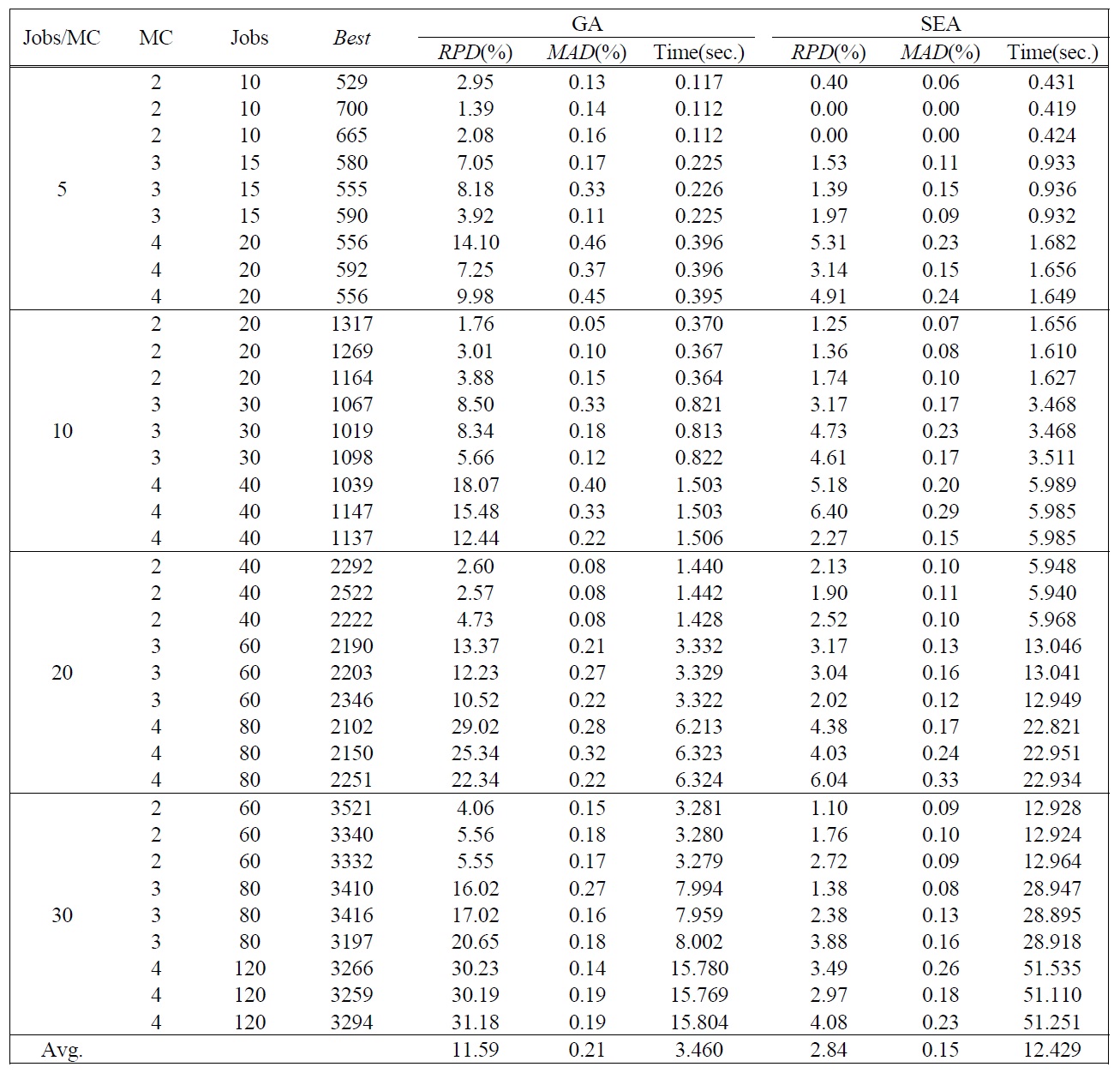
[Table 3.] Test Results of Large Sized Problems.
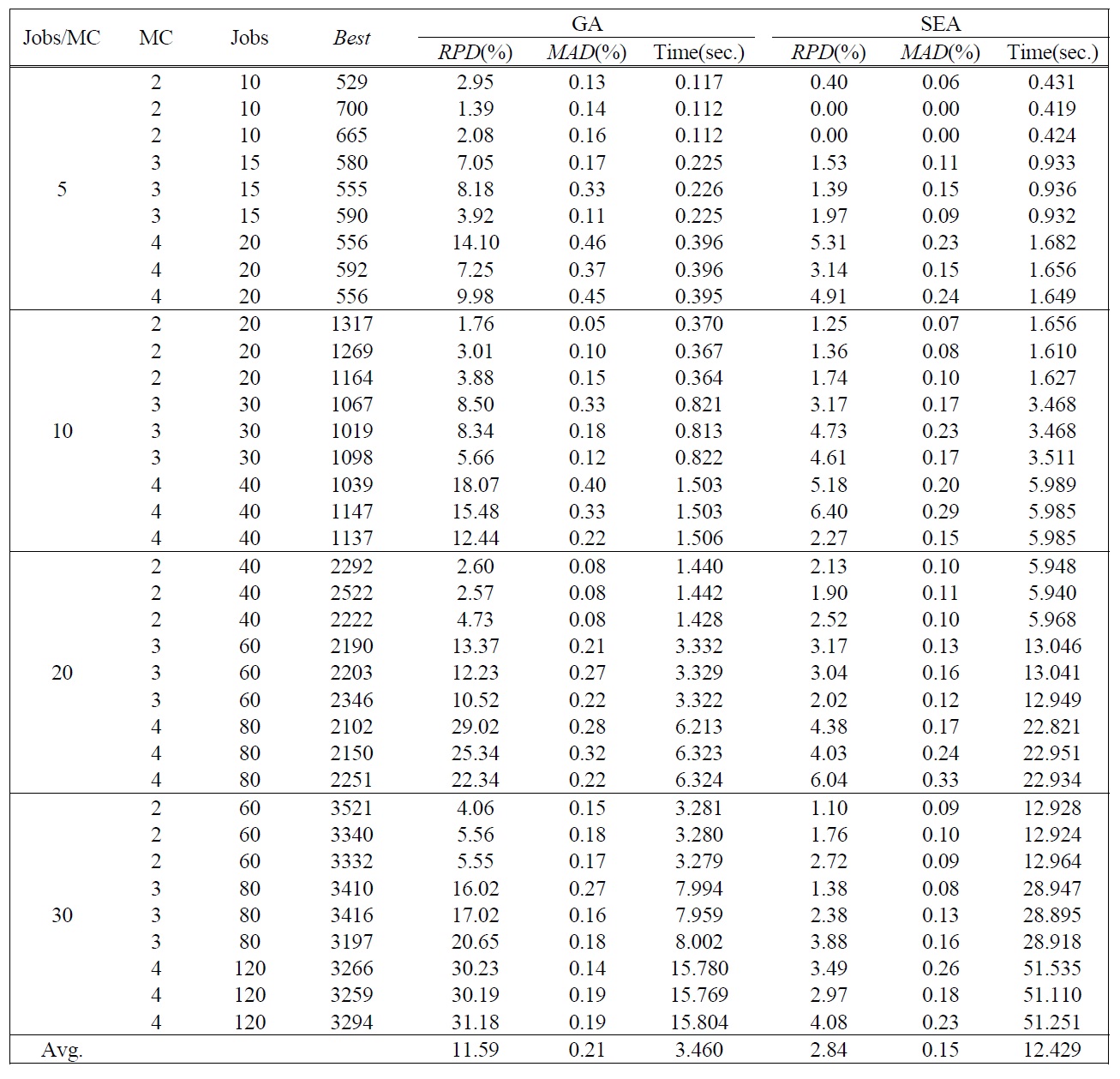
Test Results of Large Sized Problems.
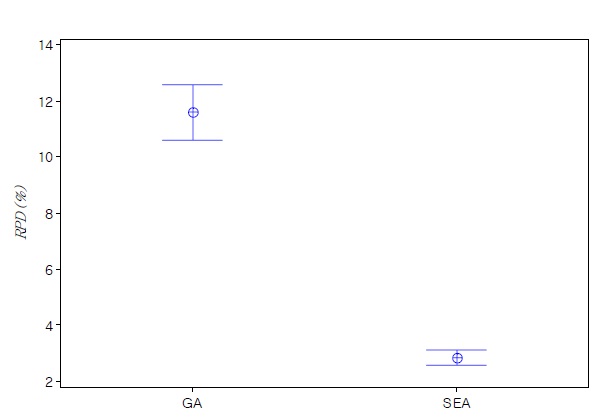
heuristic algorithms of each large sized test problem are summarized in Table 3. Similar to the results of small sized problems, we can see that SEA is more effective with low variation than the conventional GA. Average
In order to validate the results, it is interesting to check if the observed differences in the
The computation times of all test problems are summarized also in Table 2 and Table 3. The computation time of CPLEX significantly increases as the number of jobs per machine increases, and the optimal solution for the problem over total 12 jobs could not be obtained in a 3600(sec.) time limit by CPLEX. Meanwhile the computation time of GA is smaller than SEA, but the difference of the computation times is small enough to obtain solutions in a reasonable time. The difference is caused by the complexity of evolution operators for SEA.
In this paper a non-identical parallel machine scheduling problem with sequence and machine dependent setup times is considered. The objective of this problem
is to determine the allocation of jobs and the scheduling of each machine to minimize makespan. To address the problem, two different solution approaches are proposed. The first approach is based on a mixed integer programming model. Since the mathematical model is not tractable for the problems over total 12 jobs, we propose metaheuristic algorithms (GA and SEA) to increase solution efficiency. SEA is a new meta-heuristic algorithm which has a population (a set of solutions) based self-evolution mechanism. Two problem groups are tested to verify the performance of proposed meta-heuristic algorithms. The test results indicate that SEA is very effective and efficient algorithm with low variation for the non-identical parallel machine scheduling problem.
Further study is required to assess the performance of SEA with other meta-heuristics (Simulated Annealing, Tabu-search and Ant-colony optimization, etc.) in the scheduling problems or other combinatorial problems.