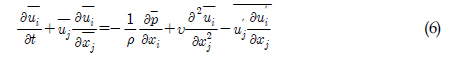최근 화석연료 고갈에 따른 대체 에너지원 개발에 대한 국제적 관심사가 높아지고 있다. 신⋅재생에너지는 지속 가능한 에너지 공급체계를 위한 미래에너지원을 그 특성으로 하며, 유가의 불안정과 기후변화협약의 규제에 대한 대응 등으로 그 중요성이 커지고 있다. 특히 지구온난화에 대해 세계적 공동 대처를 위해 체결된 기후변화협약의 후속조치로써 각국에 신재생에너지 사용 목표량이 할당되었으며, 이에 따라 국가별 신재생에너지 관련 목표달성을 위해 FIT(Feed in tariff)와 RPS(Renewable energy portfolio standard)를 시행하고 있다. 이 중 RPS는 발전사업자의 총 발전량과 판매사업자의 총 판매량의 일정비율을 신재생에너지원으로 공급 또는 판매하도록 의무화하는 제도이다. 500MW 이상의 시설을 보유한 발전 사업자에게 총 발전량에서 일정 비율을 신⋅재생에너지로 공급하도록 의무화하는 제도로 늘어나는 이산화탄소 배출량을 줄이고 신⋅재생에너지 시장을 키우기 위해 2000년 초반부터 영국, 스웨덴, 일본, 미국 등 전 세계적으로 도입하여 시행하여 왔고, 국내에서 2012년 1월 1일부터 시행되어 한전 발전자회사, 수자원공사 등 14개 대형 발전소를 공급의무자로 지정해 발전량의 일정부분을 신⋅재생에너지로 생산하도록 의무화했다. 연도별 의무 공급량 비율은 2012년 신⋅재생에너지 공급 의무량을 2%로 시작해 2024년 이후에는 10%로 점점 그 비율이 늘어나도록 시행령에 명시되어 있으므로, 앞으로 신⋅재생 에너지 발전설비의 수요는 더욱 커질 전망이다.
본 논문에서는 발전 가능한 여러 신⋅재생에너지원 중 수력 발전에 초점을 맞추었고, 특히 발전소 방수로를 이용하고자 하였다. 국내 삼천포, 보령, 당진 등 화력 발전소 및 원자력 발전소에서 냉각수로 사용되고 방류되는 방수로에는 약 3000kW 이상의 수력에너지를 보유하고 있고, 유속이 2m/sec 이상의 고유량, 고유속의 유동 에너지가 존재하여 수력발전이 가능하며, 파랑 내습이 없고 해조류, 부유물 등의 충돌 문제가 발생하지 않아 해양조건보다 발전에 매우 유리한 조건이다. 국내 방수로 발전 사례로는 삼천포 화력발전소에서 수평축 방식의 프로펠러터빈을 설치 시험하였으나 발전효율을 달성하지 못해 중단되었고, 화동 화력발전에서는 수직축 방식의 헬리컬 터빈이 설치 완료되어 추가설치를 진행 중에 있다. 그러나 방수로에 적합한 경제적이며 고효율적인 발전 시스템이 개발되지 않아 활용되지 못하고 있는 실정이며, 기술 국산화도 더딘 상태이다.
발전용 터빈은 유체의 흐름방향과 로터 축의 방향에 따라 크게 수평축 방식 터빈과 수직축 방식 터빈으로 구분된다. 수평축 방식의 터빈의 경우 유체의 흐름방향과 로터 축의 방향이 수평인 형태로써 요즘 흔히 볼 수 있는 풍력터빈이 대표적이다. 수직축 터빈의 경우 유체의 흐름방향과 로터 축의 방향이 수직인 형태로써 양력을 이용한 방식으로는 다리우스(Darrieus)터빈과 헬리컬(Helical)터빈을 들 수 있으며, 항력을 이용한 식으로는 사보니우스(Savonius)터빈이 있다. 사보니우스 터빈은 느린 유속에서 초기구동이 가능하고 큰 토크를 갖는 유리함이 있지만, 고속에서는 저항을 크게 받아 효율이 크게 감소하는 단점이 있다. 반면 다리우스 터빈은 유동 방향에 무관하게 작동되며 형상이 단순하여 중소형 터빈에 많이 사용되고 있으나, 초기 구동과 효율 측면에서 약점을 갖고 있다. 다리우스 터빈에 대한 연구는 파라메트릭 스터디를 통한 설계연구(Han et al., 2010), 캠버 형상에 따른 공력특성(Kim at al., 2010) 등의 이론 연구가 진행된 바 있다. 실험 연구로는 능동형 가변피치를 갖는 수직축 터빈에 대한 실험(Hantoro at al., 2011), 사보니우스와 다리우스를 같은 축에 설치한 Hybrid타입에 대한 실험 연구(Alam and Iqbal., 2009) 등 다양한 형태의 단일 날개를 갖는 터빈에 관한 실험이 이루어졌다. 반면 이중날개를 갖는 터빈에 대해서는 작동 종류 및 방법에 관한 이론적 특허는 상당 수 있으나, 이를 검증하는 실험 연구는 부족한 상황이다.
본 연구에서 개발하고자 하는 터빈은 다리우스 터빈과 사보니우스 터빈의 장점만을 갖도록 하고자 하였다. 이를 위해 기존의 다리우스 터빈에 회전 위치마다 각도가 달라지는 내부 날개를 추가 설치 함으로써, 다양한 유속 범위에서 운용이 가능하고 높은 효율을 갖는 이중 날개 터빈 개발을 목표로 하였다. 수치 해석을 통해 터빈 시스템의 초기설계를 수행하고, 모형실험을 통해 성능파악에 중점을 두었다.
수직축 터빈의 주요 설계변수는 터빈의 날개수(
솔리디티는 동력계수와 TSR(Tip speed ratio)의 관계에 영향이 있다. 이때 TSR은 터빈의 각속도와 유입속도의 비로 나타나는 무차원 값으로 λ로 표현한다(식 (2)).솔리디티가 높을수록 최대 효율을 갖는 TSR이 낮아짐을 확인 할 수 있으며 터빈이 회전하기 시작하는 속도인 초기 구동속도(Cut in speed) 또한 낮아진다(Lee and Lim., 2013). 본 연구에서 사용된 터빈은 내부 날개를 갖는 이중날개의 형태로서 기존 다리우스 터빈에 비해 높은 솔리디티 값을 갖는다. 이는 최대효율이 상대적으로 낮은 TSR에서 구동됨을 의미하고, 초기 구동속도 또한 낮게 형성되는 특성이 있다.
직경-스팬비는 터빈 날개의 스팬길이(
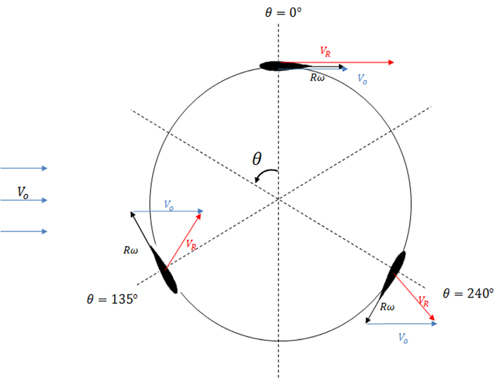
Fig. 1에 회전하는 수직축터빈의 회전위치(Azimuth position,
터빈 날개에 작용하는 상대속도(Relative velocity)는 유입 속도(
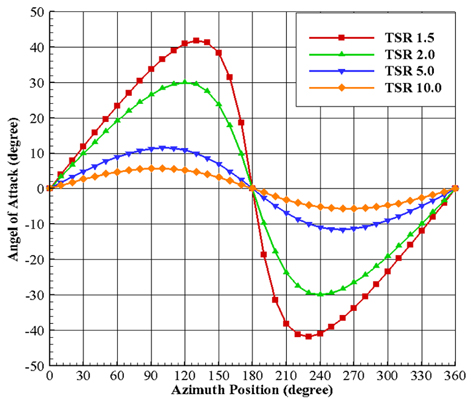
Fig. 2는 회전위치에 따른 국부 영각을 나타내며, TSR이 높을수록 국부 영각의 변화폭이 작아짐을 확인할 수 있다. 국부 영각은 터빈 날개의 토크 값 변화에 큰 영향을 주는 중요한 변수 중 하나이다. 너무 낮은 TSR은 회전 위치 당 날개의 받음각 변화가 심하여 실속이 발생하게 되어 토크 감소가 일어나게 된다. 반대로 너무 높은 TSR은 스트럿과 샤프트 등 부가물에 의한 저항이 심할 뿐만 아니라 낮은 국부 영각을 갖기 때문에 원하는 토크를 얻을 수 없다. 국부 영각의 변화는 날개 주위의 유동에 큰 영향을 미치고 나아가 토크 값에 영향을 끼쳐 터빈효율을 심하게 변하시키므로 적절한 터빈 단면과 각도를 결정하는 것이 중요하다.
즉, 날개 형상과 피치각의 변화는 양력과 항력을 변화시켜 최종적으로 토크 및 터빈 효율에 영향을 미침으로서 터빈을 제작함에 있어 중요한 요소가 된다.
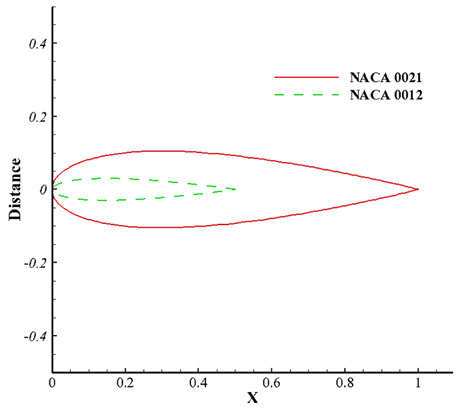
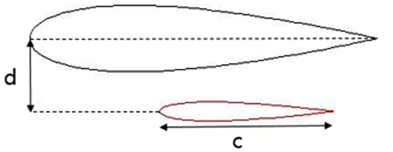
날개의 양항비를 높이기 위해 비대칭으로 설계할 경우, 특정 위치에서 대칭인 형상보다 높은 양력 값을 얻을 수 있고 이로 인한 토크 값의 향상을 얻을 수 있다. 하지만 터빈이 회전함에 따라 국부영각의 방향이 바뀌게 되어 불안정한 토크 값을 얻게 된다. 이는 여러 실험적인 수행과 수치해석적인 계산결과에서 확인 할 수 있으며 대칭인 경우가 비대칭인 경우보다 전체적인 측면에서 더 높은 효율을 갖는 것으로 나타났다. 본 연구에서 사용한 날개는 캠버가 없는 대칭형상으로써 내부날개 NACA0012와 외부날개 NACA0021을 사용하였으며 형상정보는 Fig. 3에 비교하였다.
2.3.1 점성 수치 해석
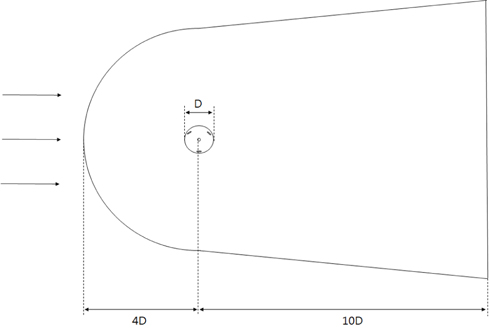
다리우스 터빈 외부 날개의 피치각도에 대한 성능을 평가하기 위해 유동해석 상용프로그램인 ANSYS 사의 FLUENT 15.0을 사용하여 2차원 터빈의 성능해석을 수행하였다. 계산 영역은 Fig. 4에 나와 있으며, Sliding mesh 구역의 지름(
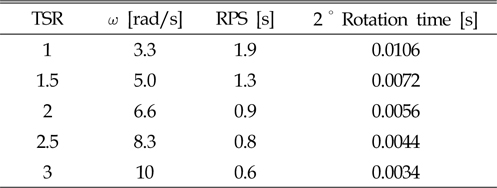
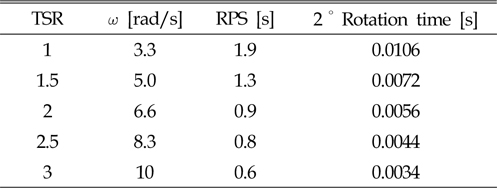
TSR에 따른 효율을 측정하기 위해 Sliding mesh 구역의 회전 시간을 TSR 1부터 TSR 3까지 0.5간격으로 변화를 주었다. 각각 TSR에 해당하는 각속도와 RPS(Revolution per second)을 계산한 뒤 2°회전 시에 걸리는 시간에 대한 계산 결과를 Table 1에 나타내었다.
Analysis parameter
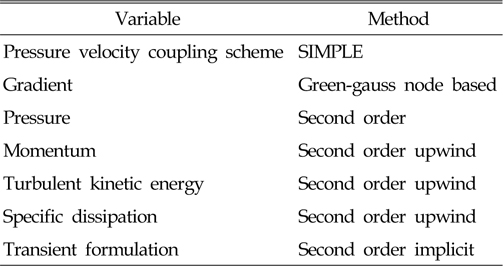
점성 수치 해석의 기본 방정식은 Navier-Stokes 방정식이며 이산화 방식은 유한체적법으로 3차원 비압축성 비정상 유동조건하에서 해석이 수행된다. 비정상 유동조건의 지배방정식은 Newton유체 조건에서 다음 식 (5), (6)의 연속방정식과 운동량 방정식으로 다음과 같이 표현된다.
난류 모델은 복잡한 회전체 유동영역 해석에서 정확성이 높다고 알려진 k-
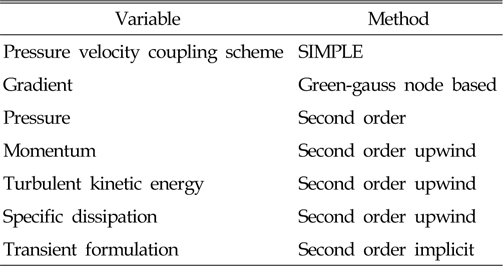
[Table 2] Numerical modeling parameters
Numerical modeling parameters
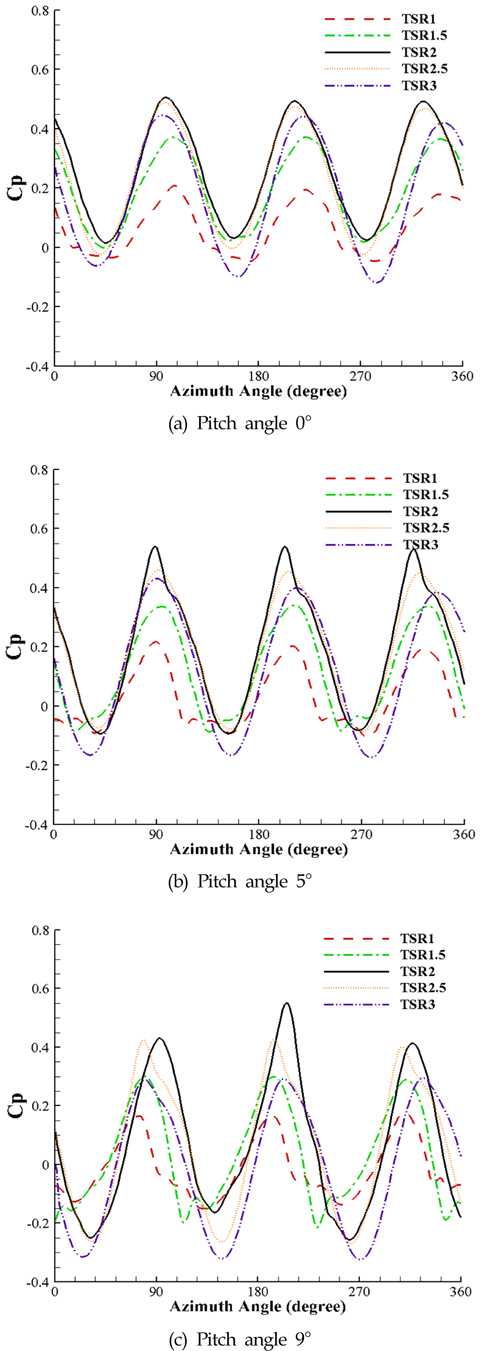
피치각이 없는 0도를 기준으로 하여, +5도와 -5도에 대해 수행하였고, 추가적인 +9도의 경우에 대해 계산하였다. 양의 방향은 터빈회전 반경을 기준으로 바깥을 의미한다.
터빈 효율은 식 (7)과 같이 토크계수와 TSR의 곱으로 정리할 수 있다. Fig. 5는 외부 날개의 피치각 변화에 따른 효율 특성을 보여주며, 피치각이 커짐에 따라 효율의 변화폭이 커지는 것을 확인하였으며, 각각의 피치각도에 대해 TSR=2인 경우 가장 높은 효율이 나타났다.
여기서
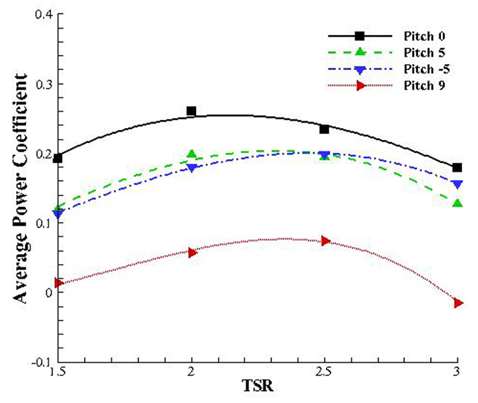
앞선 결과를 피치각 변화에 따른 TSR 대 평균 동력계수 값을 Fig. 6에 나타내었다. 터빈은 날개형상, 솔리디티 등에 따라 터빈시스템이 갖는 최적의 피치각도가 존재하게 되는데, 본 연구에서 설계된 터빈은 피치 각이 0도에서 가장 높은 효율을 갖는 것을 확인하였다.
2.3.2 비점성 수치 해석
내부 날개의 경우 형상, 코드길이, 외부 날개와의 거리 등 다양한 설계 변수를 고려해야 한다. 이를 위해 상대적으로 계산시간이 매우 짧은 비점성해석법(포텐셜 기반 패널법)을 사용하였다(Sakir Bal, 1997). 터빈날개에 작용하는 토크계수는 식 (8)로 날개가 갖는 양력 값과 항력 값에 영향을 받는 것을 알 수 있는데, 실속(Stall)이전에서는 양력이 주요변수로 작용하기 때문에 양력계수만을 비교하였다.
캠버가 없는 대칭형 단일 날개를 갖는 터빈의 경우 날개에 작용하는 상대속도에 대한 국부 영각이 회전함에 있어 방향이 바뀌어도 형상이 대칭이기 때문에 한 방향으로 해석이 가능하다 (Fig. 1참조). 하지만 이중 날개의 경우 두 날개 사이에 간섭이 일어나 양력계수의 변화가 생김으로 회전함에 따라 받는 국부영각 방향을 고려해야 한다. 따라서 앞선 점성해석을 통해 얻은 최대효율을 갖는다고 판단한 TSR2조건일 때, 회전위치 45°와 315°에서 계산을 수행하였다. 각각 경우에 대해 내부날개의 크기와 이격 거리를 바꾸어 가며 양력계수를 계산 하였고, 이 결과를 토대로 효율을 평가하였다.
먼저 내부 날개의 크기를 외부날개의 0.5, 1.0, 2.0 배로 변화시켜 가면서 계산된 양력계수 값을 Fig. 7에 비교하였다. 내부날개가 외부날개의 2배인 경우에는 단독(w/o blade) 일 때 보다 효율이 더 떨어지는 것을 확인하였으며, 0.5배인 경우에서는 좌우 값의 변동이 크지만 전반적으로 단독일 때의 계수 값보다 큰 것을 확인 하였다. 이 결과를 토대로 내부날개의 크기는 외부날개에 비해 작은 것이 더 효율적이라 판단하였다.
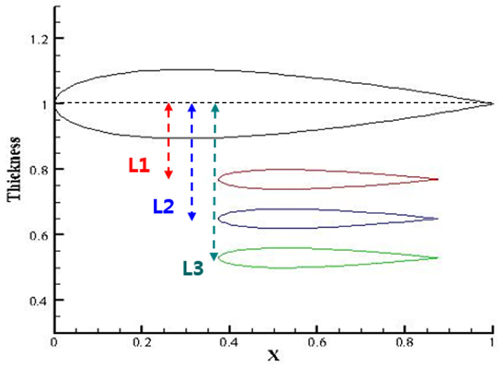
내부날개의 크기를 결정한 상태에서 외부날개로부터 내부날개까지의 거리 변화에 대한 특성을 살펴보기 위해 Fig. 8과 같이 외부날개와 내부날개의 거리를(
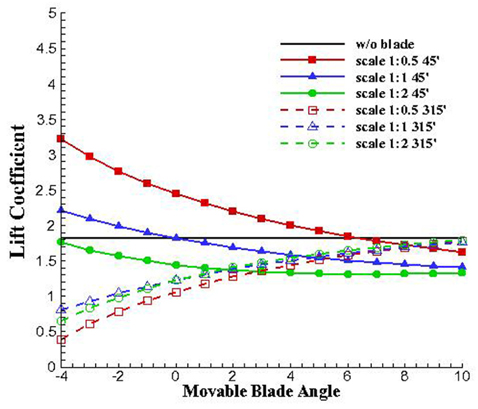
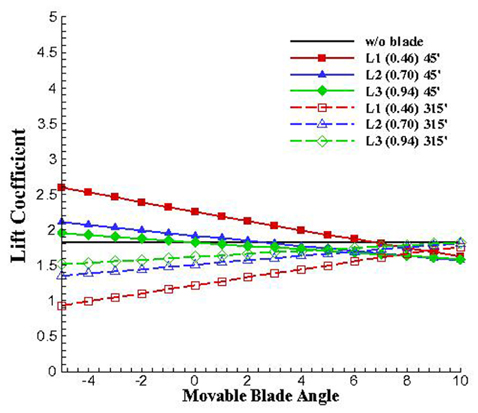
Fig. 9와 같이 3종의 이격 거리를 고려하였고, Table 3에 자세한 거리를 나타내었다. 각 이격 거리에 따라 내부날개를 -5°에서 10°까지 변화시켜 가며 양력계수를 구하였고, 그 결과를 Fig. 10에 나타내었다. 그래프의 실선은 45°, 점선은 315°에 대한 양력계수 값을 나타낸다. 그 결과, 내부날개의 각도에 따라 외부날개의 양력계수 값의 변화가 반대되는 경향이 확인 되었고, 각도에 따라 값이 크게 달라지는 특징을 볼 수 있었다.
[Table 3] Non-dimension distance

Non-dimension distance
45°에서는 날개 안쪽으로 들어간 -5°에서 간격이 좁을수록 큰 값을 갖지만, 315°에서는 바깥으로 벌어진 10°에서 간격이 멀수록 큰 값을 갖는 것을 확인하였다. 가장 큰 양력계수 값을 갖는 위치에서 내부날개가 없을 때(w/o blade)때와 비교해 보았을 때, 45°의 경우 가까운 위치 (1)에서 뚜렷하게 큰 값을 보이는 반면, 315°에서는 큰 차이가 나지 않았다. 이를 토대로 내부전체적인 효율을 따져 보았을 때 안정적인 값은 중간 (2)위치로 판단된다.
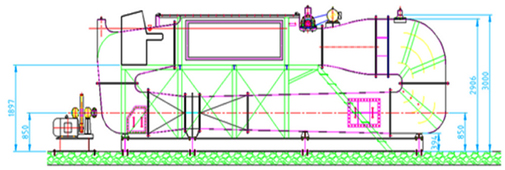
수치해석을 통해 얻은 결과를 토대로 개념 설계를 수행하였고, 이를 통해 도출된 개발 수류터빈 모형의 주요 치수와 설계 모형은 Table 4와 Fig. 11 (a), (b)에 나타내었다. 터빈의 회전에너지 손실을 줄이기 위해 터빈 축 상하에 베어링을 설치하여 축의 흔들림을 제어하였고, 무게와 구조강도, 부식 등을 고려하여 알루미늄으로 제작하였다. 먼저 터빈의 단독성능 평가를 위해 외부날개만 있는 경우(Single), 내부 날개가 고정되어 있는 경우(Dual-fixed)와 가변하는 경우(Dual-movable)에 대해 실험을 수행하였다. 여기서 외부 날개로부터 내부 날개까지의 거리 변화에 대한 실험적 특성을 살펴보기 위해 L1, L2, L3 떨어져 있는 경우(Fig. 11 (c))에 대해 실험을 수행하였다.

Specification
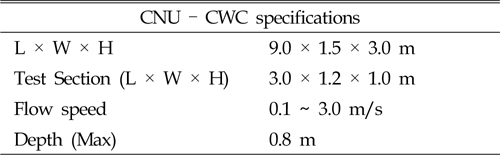
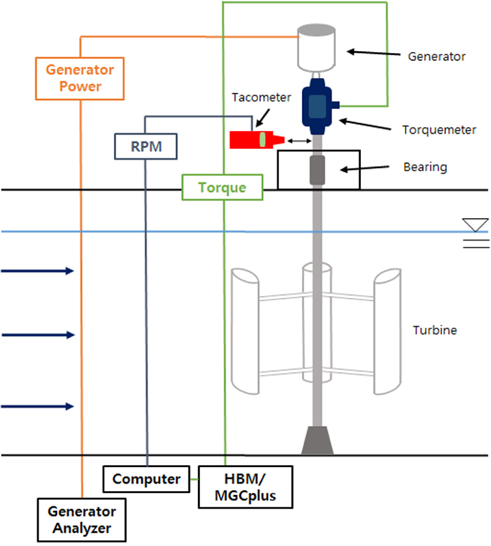
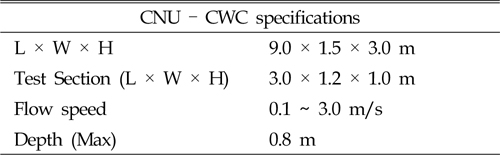
모형실험 평가는 시험부 길이가 3m, 폭 1.2m, 깊이 1m인 충남대학교 회류수조(Fig. 12, Table 5)에서 실시하였고, 실험에 앞서 회류수조의 유속 정보에 대한 측정과 분석이 선행 되었다. 실험 유속은 0.1m/s 간격으로 1m/s까지 증가시키면서 토크, RPM(Revolution per minute)을 측정하여 분석하였다. 토크 측정은 10N-m급의 토크미터를 제작하여 HBM사의 MGCPlus를 통해 초당 50개의 데이터를 수집하였고, 타코미터로 RPM을 측정하였다. Fig. 13은 토크미터와 실험측정 장비를 보여주며, Fig. 14는 실험 모형 및 계측 시스템 구성도를 보여준다.
[Table 5] CNU ? CWC specifications
CNU ? CWC specifications
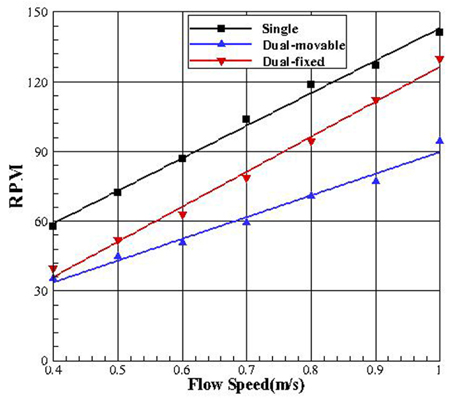
먼저 유속 변화에 따른 수류터빈의 회전수(RPM)를 측정하였다(Fig. 15). 시험 유속범위에서 외부날개 단독인 경우가 가장 높았으며, 내부날개 고정인 경우(Dual-fixed), 가변하는 경우 (Dual-movable) 순으로 나타났다. 특히 내부 날개가 고정된 경우를 보면 외부날개 단독인 경우와 비슷한 회전수 증가를 보였지만, 내부 날개가 가변하는 경우에는 증가 비율이 낮아지는 것을 확인 할 수 있었다.
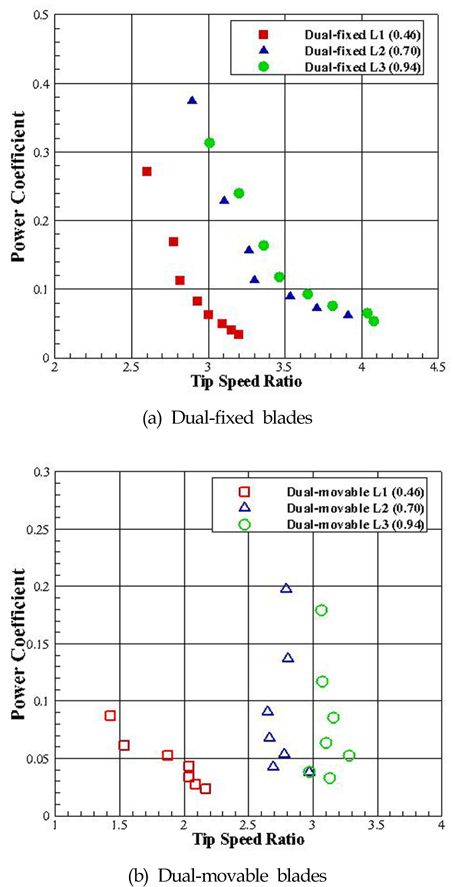
Fig. 16은 내부날개 고정인 경우, 가변하는 경우에 대해 내부날개의 위치변화에 따른 효율특성을 TSR에 따른 터빈효율 (Turbine power coefficient)로 평가하였다.
먼저 Fig. 16 (a)는 내부날개 고정인 경우에 대한 TSR에 따른 터빈 효율 값으로 외부날개로부터 L2 위치에 내부날개가 설치된 경우 가장 큰 효율이 발생함을 알 수 있다. Fig. 16 (b)는 내부날개가 가변하는 경우로 고정된 경우에 비해 전체적으로 효율은 낮아지며, 특히 L2, L3인 경우 TSR의 변화가 없는 것을 확인할 수 있다. 즉 가변하는 내부날개의 영향으로 시험유속 범위에서 일정한 TSR이 나타남을 알 수 있다. 특징적으로 두 경우 모두 이격 거리가 증가 할수록 높은 TSR에서 작동됨이 관측 되었다.
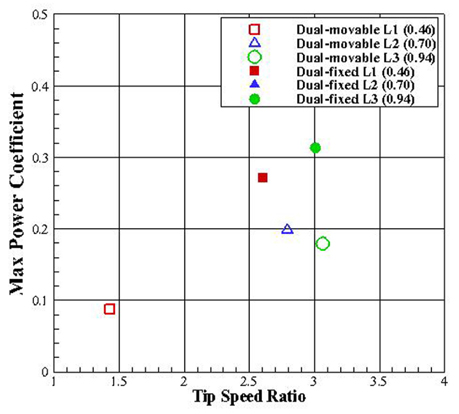
Fig. 17에 위 두 방식의 각 경우에 대해 최대 효율을 비교하였다. 가변하는 경우에 비해 고정된 경우에서 더 큰 터빈 효율값이 측정 되었고, 두 경우 모두 L2에서 가장 큰 효율을 갖는 것을 알 수 있다. 이는 실험결과 최대 효율을 갖는 내부 날개위치와 비점성 해석 결과를 통해 얻은, 효율이 안정적이라고 생각되는 내부 날개 위치가 일치 하는 것으로 나타났다.
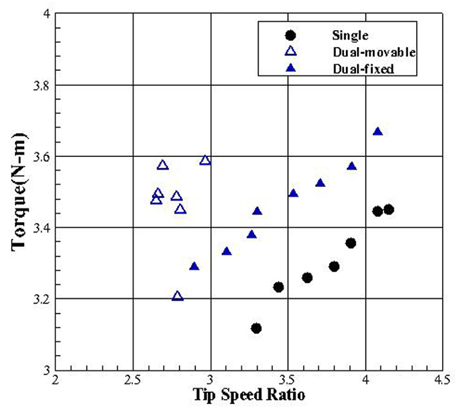
Fig. 18은 최대 효율이 나타나는 외부날개 단독, 내부날개 고정과 가변인 경우에 대해 시험 유속 범위에서의 해당 TSR에서 계측된 토크 값을 보여준다. 먼저, 내부날개가 추가된 경우 외부날개 단독일 때 보다 더 큰 토크값을 갖는다는 것이 확인 되었고, 외부날개 단독인 경우와, 내부날개 고정인 경우 TSR이 증가하면서 토크 값도 함께 증가하는 것이 확인 되었다. 하지만 내부날개 가변의 경우 전체 유속범위에서 TSR과 토크 값이 일정하게 나타나는 것이 확인 되었다.
본 연구에서는 신재생에너지 의무할당제 제도에 적극 대응할 수 있는 수류터빈을 개발하기 위해, 저속에서 초기구동이 가능하고, 다양한 유속에서 일정한 토크를 갖는 다리우스 터빈과 사보니우스 터빈의 장점을 결합한 가변형 이중 날개를 갖는 수류터빈을 개발하고자 하였다.
먼저 내부날개의 자유도 여부에 상관없이 외부날개와의 이격 거리는 최대효율 특성에 영향을 미침을 확인하였다. 또한 내부날개가 고정된 경우 상대적으로 낮은 유속에서 최대효율이 나타남을 확인하였고, 내부날개가 가변하는 경우에는 넓은 유속 범위에서 TSR과 작용하는 토크 값이 일정하게 나타남을 확인하였다. 이는 유속이 일정하지 않는 곳에서도 특정 TSR 부근에서 일정한 수준의 토크 값을 기대할 수 있음을 의미하고, 토크의 크기를 증가 시킬 수 있다면 넓은 유속범위에서 안정적인 발전을 기대 할 수 있다.