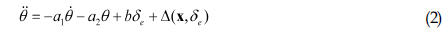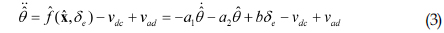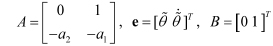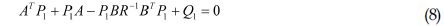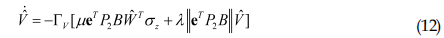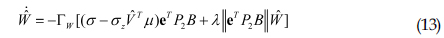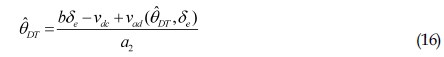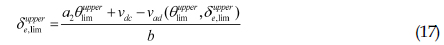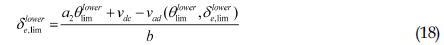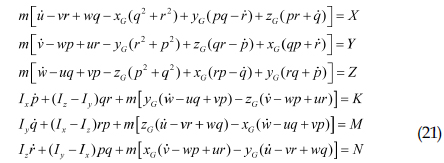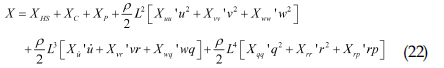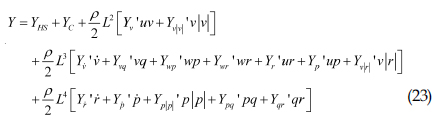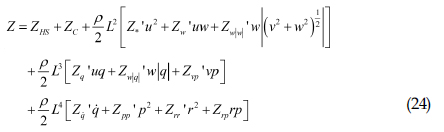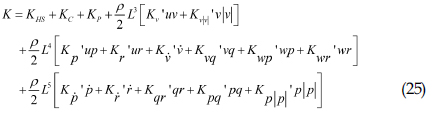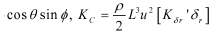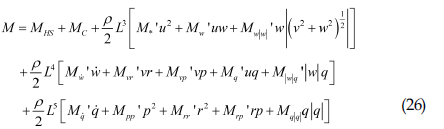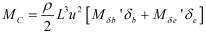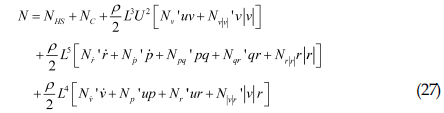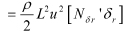안전운항영역은 운동체가 안전하게 운항할 수 있는 영역을 의미하고 항공기나 잠수함 등의 다양한 운동체에 대하여 적용 가능한 개념이다. 잠수함의 경우 안전운항영역은 선속, 심도, 종동요각에 의해서 정의된다. 깊어질수록 증가하는 수압으로 인하여 발생할 수 있는 선체의 손상을 방지하기 위한 최대안전심도가 설정되고, 수면 근처에서 운항하는 경우 파 강제력 및 흡입력으로 인해 선체가 수면위로 끌리는 것을 방지하기 위하여 최소안전심도가 설정된다. 과도한 종동요각으로 인해 추진계통이 손상을 받게 되거나 다른 예기치 못한 손상을 입을 가능성이 있으므로 이를 방지하기 위해 종동요각 제한이 설정된다. 이러한 제한을 벗어나는 것을 방지하기 위하여 속도 별 운항가능 심도에 대한 안전운항영역 도표를 작성하고 조타수에게 전달 및 숙지 시키거나, 심도변경 시 완만한 심도경로를 생성 한 후 이를 추종하도록 잠수함을 제어하는 방식으로 종동요각을 보호하는 등의 다소 수동적인 방법으로 제한된 변수(한계변수)들을 보호하고 있다.
운항영역 보호시스템은 운동체의 구조적 한계, 동역학적 한계, 제어입력의 한계를 초과하지 않고 고유의 운항영역 내에서 자유롭게 운항할 수 있도록 하는 시스템이다(Shin et al., 2010). 운항영역 보호시스템은 보수적으로 접근할 수 밖에 없는 운항 영역의 경계를 넘지 않도록 보장함으로써 운항사고를 줄일 수 있고, 영역의 경계를 충분히 활용한 효율적인 임무수행을 가능하게 한다. 또한 제한되어야 하는 상태들을 모니터링 하고 제어해야 하는 조종사의 업무부담을 경감시킬 수 있다.
운항영역 보호시스템에 관한 연구는 주로 항공분야에서 활발하게 이루어졌다. 조종면이 유압장치를 통해 연결되어 있는 방식이었던 1980년대 이후 전기적 신호로 조종면을 제어하는 Fly-by-wire 방식으로 바뀜에 따라 자동제어 및 운항영역 보호에 대한 개념이 중요하게 부각되었다. 운항영역 보호 알고리즘으로는 Fixed horizon prediction, 동적 트림 알고리즘, Peak response estimation, Non-iterative adaptive limit estimation 등이 있다(Sahani, 2005). Fixed horizon prediction은 한계변수의 어떠한 시간간격 후의 값을 예측하는 방법이다(Bateman, 1998). 미래의 한계변수 값을 예측하기 위해서 한계변수와 제어입력, 그리고 시간간격간의 관계식이 필요하다. 이 알고리즘은 1초 남짓한 미래의 값밖에 예측할 수 없다는 단점이 있다. 동적 트림 알고리즘은 Horn et al.(1998)이 제안한 개념으로, 준 정상상태에 대한 개념을 이용하여 한계변수가 한계점을 초과하게 되는 제어입력을 추정하는 방식이다. 다양한 운항 조건에도 적응할 수 있는 on-line training 방식의 인공신경망을 이용한 adaptive 동적 트림 알고리즘이 Horn et al.(2002), Unnikrishnan et al.(2003), Yavrucuk et al.(2002), Yavrucuk(2003)에 의하여 제안되었다. Peak response estimation은 과도응답을 갖는 동역학에 적합한 알고리즘이다. 이 알고리즘은 제어입력으로 인해 즉각 발생하는 과도응답의 고점을 추정하는 알고리즘으로, 로터 허브(Rotor hub) 모멘트와 플랩핑(Flapping)의 한계를 피하기 위한 알고리즘으로 사용되었다(Horn and Sahani, 2004). Non-iterative adaptive limit estimation은 adaptive 동적 트림 알고리즘에서 필요로 하는 반복계산을 제거한 알고리즘으로, Gursoy and Yavrucuk(2015)에 의해서 개발되었다. 위와 같은 알고리즘을 이용하여 설계된 운항영역 보호시스템이 고정익 항공기, 회전익 항공기, 무인항공기 등 다양한 항공기에 적용한 사례가 문헌에 다수 보고되고 있다(Yavrucuk et al., 2009; Shin et al., 2011; Falkena et al., 2011; Gursoy and Yavrucuk, 2013). 앞서 설명한 항공분야와 같이 능동적인 운항영역 보호시스템 설계 및 적용에 관한 사례는 잠수함의 조종 및 제어에 관련된 문헌에 보고된 바 없다.
본 연구에서는 종동요각에 대한 잠수함의 운항영역 보호시스템을 설계하기 위하여 종동요 운동을 모사하기 위한 추정모형을 만들고 오차 방정식을 구성하였다. 오차 방정식을 안정화 시키기 위한 선형보상기는 Linear quadratic regulator(LQR)을 이용하여 설계하였다. 모델링 불확실성을 추정하기 위하여 인공신경망을 이용한 적응제어기를 설계하였다. 한계예측 알고리즘은 제한하고자 하는 변수의 운동특성을 고려하여 설계하여야 한다. 잠수함의 종동요는 일정한 선미제어판각에 과도응답을 갖지 않고 정상상태로 수렴하는 경향을 갖고 있기 때문에 이러한 운동특성에 적합한 동적 트림 알고리즘을 이용하여 한계예측 알고리즘을 작성하였다. 잠수함의 심도제어 시뮬레이션에 설계된 운항영역 보호시스템을 적용시켜 그 성능을 확인하였다.
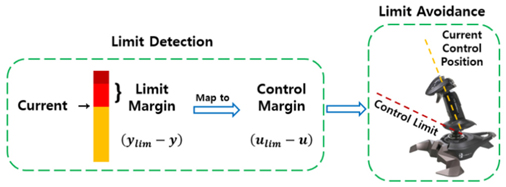
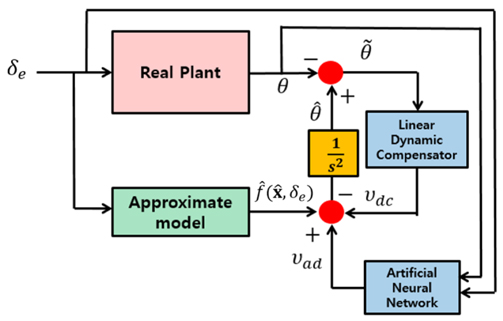
운항영역 보호시스템은 한계예측과 한계회피로 구성할 수 있다. 한계예측은 잠수함의 상태와 제어입력을 바탕으로 운항영역 경계를 벗어나지 않도록 하는 제어입력의 한계 및 제어입력의 여유(Margin)를 계산한다. 한계회피는 한계예측에서 계산된 제어입력의 한계를 초과하지 않도록 하는 과정을 의미한다. Hard 운항영역보호(Hard envelope protection) 방식은 주로 오토파일럿으로 운동체를 제어하는 경우에 사용되는 방법으로, 심도제어기와 같은 하위제어기(Low level controller)에서 출력되는 제어입력 신호에 제한을 걸어주는 방법으로 한계를 회피하는 방법이다. Soft 운항영역보호(Soft envelope protection) 방식은 조종사가 수동으로 운동체를 제어하는 경우에 사용되는 방법으로, 한계예측에서 계산된 제어입력의 여유를 바탕으로 스틱을 통한 진동신호나 시각 및 청각적인 신호를 통해 경고를 하여 조종사가 스스로 제한을 벗어나지 않도록 하는 방식이다. 따라서 soft 운항영역보호방식의 운항영역 보호시스템은 한계예측 알고리즘 설계까지를 운항영역 보호시스템 설계라고 정의할 수 있다. 본 연구는 조타수가 수동으로 잠수함을 제어한다고 가정하고 Soft 운항영역보호방식의 운항영역 보호시스템을 설계하였다. Fig. 1에 운항영역 보호시스템의 개념도를 도시하였다.
한계예측을 하기 위해서 제한하고자 하는 변수의 실제동역학을 추정해야 한다. 본 연구에서 제한하고자 하는 변수는 종동요각이다. 잠수함의 종동요는 다음과 같은 일반적인 비선형 함수로 표현할 수 있다.
여기서,
식 (2)의
여기서, 는 추정모형의 종동요각을 의미하고, 는 를 의미한다. 식 (3)에서 식 (2)를 빼주면 식 (4)와 같은 오차동역학을 구성할 수 있다.
여기서 는 추정모형과 잠수함의 종동요각 간의 오차로 를 의미한다. 식 (4)를 행렬식으로 표현하면 식 (5)와 같다.
여기서,
적응제어신호
선형보상기는 식 (5)에 표현되어 있는 오차방정식을 안정화시키기 위하여 필요하다. 만약 적응제어신호가 모델링 불확실성을 잘 추정한다고 가정하면, 식 (5)는 아래와 같이 표현할 수 있다.
선형보상기의 성능은 식 (6)에서 표현된 오차벡터와 선형보상기신호의 크기로 판별할 수 있다. 최소화 시켜야 하는 두 변수를 이차식 형태로 표현한 성능지수를 식 (7)과 같이 설정해 보자.
적응제어기는 오차방정식에서 표현되어 있는 모델링 불확실성을 추정하기 위하여 사용된다. 인공신경망은 구조를 알 수 없는 함수를 주어진 입력 변수들 간 비선형 조합을 이용하여 근사화 하기 때문에 예측능력이 우수하다. 본 연구에서는 Park et al.(2015)의 연구를 참고하여 단일은닉층(Single hidden layer)을 갖는 인공신경망을 사용하여 적응제어기를 설계하였다. 적응제어기의 출력인 적응제어신호는 식 (10)과 같이 표현할 수 있다.
여기서
여기서
동적 트림 알고리즘은 준 정상상태에 대한 개념을 이용하여 제한되어야 하는 변수가 한계를 초과하지 않도록 하는 제어입력을 추정하는 방식이다. 준 정상상태에서는 종동요각의 시간에 대한 미분값이 모두 0이 된다. 이를 식으로 표현하면 식 (15)와 같다.
식 (15)와 같은 가정을 추정모형의 동역학을 표현한 식 (3)에 적용하면 식 (16)을 얻을 수 있다.
여기서 는 동적 트림 가정을 적용한 추정모형의 종동요각을 의미한다. 정의에 따르면 제어입력한계는 동적 트림의 반응이 설정된 한계치와 같아질 때의 제어입력값을 의미한다. 종동요각 한계의 상한값을 , 하한값을 로 정의하자. 식 (16)을 이용하여 종동요각 한계의 상한값과 하한값에 상응하는 제어입력의 상한값 과 하한값 을 표현하면 식 (17), (18)과 같다.
위의 식을 보면, 비선형 방정식의 양변에 구해야 하는 변수가 들어가 있기 때문에 반복계산을 이용해야 한다. 본 연구에서는 고정점 반복법(Fixed-point iteraion)을 이용하여 해를 구하였다. 반복계산의 초기값은 바로 전 스텝에서 계산된 해를 이용하는 것이 효과적이다는 Unnikrishnan et al.(2003)의 연구를 인용하여 본 연구에 적용하였다.
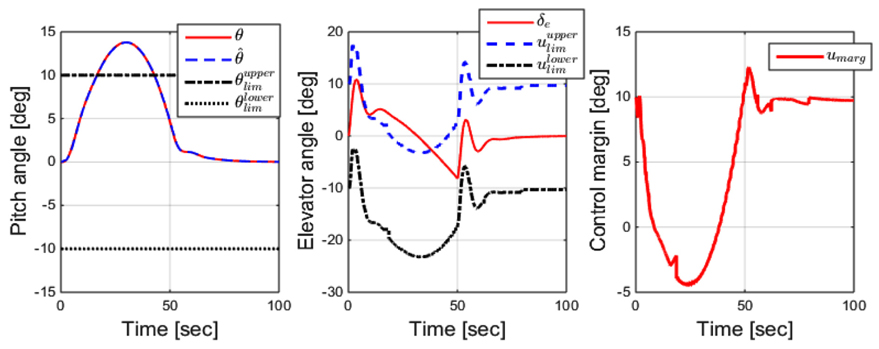
잠수함이 심도제어를 하는 한 가지 상황에 대해 종동요각의 한계를 각기 다르게 설정하였을 때 계산되는 제어입력의 한계와 제어입력의 여유를 도출해 보는 방법으로 설계된 운항영역 보호시스템의 성능을 확인해 보았다. 심도변경시 발생하는 종동요각은 대략 20° 정도에서 제한하는 것이 관례이지만, 최대 종동요 각은 실제적으로 거의 적용되지 않고 있고 보편적으로 종동요각을 5°~10°로 제한하고 있다(Burcher and Rydill, 1995). 본 논문에서는 종동요각의 한계를 ±10°와 ±20°로 설정하였다. 잠수함의 선속은 12m/s, 선미제어판의 최대각도는 30°로 설정하였고 제어판의 동역학은 식 (19)와 같은 1차 동역학으로 가정하였다.
여기서 시정수
종동요각은 선수가 위를 향하는 경우를 양수로, 심도의 경우 연직 하방을 양의
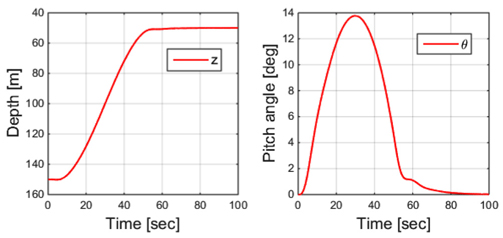
Fig. 4의 첫번째 그래프는 설정된 종동요각 한계와 잠수함의 종동요각, 그리고 추정모형의 종동요각을 보여준다. 잠수함의 종동요각을 보면 약 16초부터 43초까지 약 27초간 제한된 종동요각 10°를 벗어나는 것을 알 수 있다. 두번째 그래프는 제어입력인 선미제어판각과 한계예측으로 계산되는 제어입력한계의 상⋅하한값을 보여준다. 결과를 보면 약 8초부터 38초까지 선미제어판각이 제어입력의 상한값을 초과하는 것을 알 수 있다. 세번째 그래프는 계산된 제어입력의 여유를 보여준다. 제어입력의 여유를 보면 초기 10°에서 잠수함의 종동요각이 제한된 값에 가까워 지면서 점점 줄어드는 것을 확인할 수 있다. 종동요각은 약 16초부터 설정된 한계를 초과하게 되고 제어입력의 여유는 약 8초부터 음수를 갖게 된다. 이는 잠수함이 현재의 제어입력을 가지고 운동한다면 종동요각 한계를 초과한다고 8초라는 시점에 미리 예측하기 때문에 제어입력의 여유가 음수를 갖게 된다고 해석된다. 만약 제어입력의 여유의 크기와 경향성을 함수로 하는 한계회피 알고리즘을 작성하여 적용한다면 종동요각 한계를 초과한다고 예측하는 8초라는 시점 이전에 한계회피를 수행할 것이기 때문에 종동요각 한계를 초과하지 않을 것이라 예상된다.
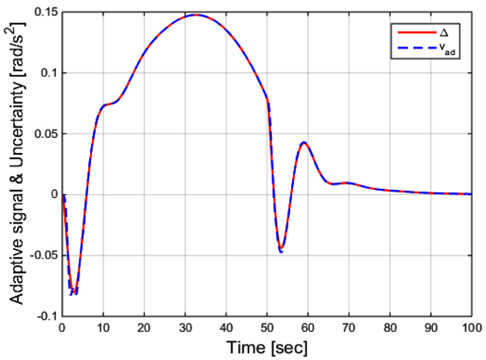
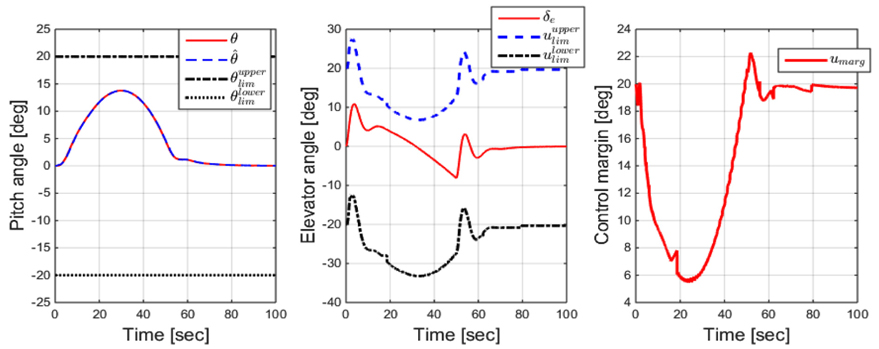
Fig. 5는 모델링 불확실성과 적응제어신호를 비교한 결과를 보여준다. 결과에서 알 수 있듯 적응제어신호가 모델링 불확실성을 잘 보상하는 것을 알 수 있다. 모델링 불확실성을 잘 보상하기 때문에 Fig. 4에서 추정모형의 종동요각 이 잠수함의 실제 종동요각을 잘 추종하는 것을 알 수 있다. 다음으로 앞선 심도제어 시뮬레이션과 동일한 조건에서 종동요각 한계를 20°로 설정했을 때의 한계예측 계산결과를 도시해 보았다.
결과에서 알 수 있듯 종동요각 한계가 20°로 설정되었고, 종동요각이 설정된 한계를 벗어나지 않기 때문에 제어입력의 여유가 전체 시뮬레이션 시간에 걸쳐 항상 양수임을 알 수 있다. Fig. 4 ~ Fig. 6에 수록된 시뮬레이션 결과들에서 알 수 있듯이, 운항영역 보호시스템은 종동요각과 설정된 한계치간의 여유를 실질적으로 종동요각을 제어하는 선미제어판의 여유로 맵핑(Mapping)시켜 준다. 따라서, 기존 시스템은 종동요각 한계치를 넘지 않도록 직관에 의존하여 제어판을 조작해야 하는 반면, 운항영역 보호시스템은 보다 정량적인 수치를 기반으로 제어 가능하게 함으로써 잠수함 운항안정성 향상에 기여할 수 있다.
본 논문에서는 잠수함의 종동요각을 보호할 수 있는 운항영역 보호시스템을 설계하였다. 잠수함의 실제 종동요 운동을 추정하기 위하여 인공신경망과 LQR제어기법이 사용되었다. 한계변수가 한계치를 넘게 되는 제어입력한계를 예측하기 위해서 동적 트림 알고리즘을 사용하였다. 제어입력한계를 구하기 위한 방정식의 해는 고정점 반복법을 이용하여 구하였다. 설계된 운항영역 보호시스템을 Gertler 모형을 이용하여 작성된 잠수함 조종운동 시뮬레이션 프로그램에 적용하였다. 적용 결과 운항영역 보호시스템이 잠수함의 운동을 예측하며 제어입력의 한계와 여유를 효과적으로 예측하는 것을 알 수 있었다. 그러나 본 연구는 잠수함에서 정의하는 한계변수 중 종동요각만을 보호하는 시스템을 설계한 것이므로, 속도 및 심도와 같은 다른 한계변수도 보호할 수 있는 시스템 설계에 대한 추가적 연구가 필요하다. 한계회피 알고리즘을 추가하고 완전 무인화하여 조타수의 조종없이 설정된 제한을 넘지 않는 것을 보장하는 Carefree maneuvering 시스템을 구축하는 것도 의미있을 것이라 판단된다. 또한 본 연구에서 사용한 동적 트림 알고리즘 외에 Peak response estimation과 같은 다른 알고리즘을 적용한 시뮬레이션 결과를 얻는다면, 잠수함에 최적화된 운항영역 보호시스템 설계방법에 대한 유의미한 결과를 도출할 수 있을 것으로 기대된다.
설계된 운항영역 보호시스템 성능검증을 위한 시뮬레이션은 서울대학교에서 개발한 잠수함 조종성능해석 프로그램인 Submarine maneuvering simulation program(SMSP)를 통하여 수행되었다. 대상 잠수함은 개념설계 단계에 있는 잠수함으로서, 길이 대 직경비가 10.9이고 세일의 리딩에지가 선미로부터 0.75L에 위치한다. 잠수함의 제어를 위하여 선수 제어판과 선미에 십자형으로 된 제어판을 장착하고 있다. SMSP는 식 (21)과 같은 6자유도 운동방정식을 기반으로 작성되었다.
식 (21)의 우변은 잠수함에 작용하는 외력을 의미한다. SMSP의 잠수함에 작용하는 외력은 Gertler and Hagen(1967)의 연구를 참고하여 작성되었고, 이를 식으로 표현하면 식 (22)~(27)과 같다.
• 전후동요:
여기서,
• 좌우동요:
여기서,
• 상하동요:
여기서,
• 횡동요:
여기서,
• 종동요:
여기서,
• 선수동요:
여기서,
동유체력 모형의 유체력 미계수는 수조모형시험과 풍동모형시험의 결과를 이용하여 도출되었다. 저항시험-평면운동장치시험(Planar motion mechanism test)-원추형 시험(Coning motion test)이 수조에서 수행되었고, 연성사항시험-제어판시험이 풍동에서 수행되었다. 모형시험 데이터로부터 유체력 미계수를 도출하기 위해 최소자승법(Least square)-황금분할법(Golden section method)-Fourier해석과 같은 데이터 해석방법이 사용되었다.