전 세계적으로 석유 및 천연가스 등의 화석연료에 대한 수요가 증가하고, 연안역의 자원이 고갈되어 감에 따라 자원 개발 영역이 심해역으로 이동하고 있다. 수심이 얕은 해역에서 주로 사용되어온 고정식 구조물은 설치 수심이 깊어지면서 건조 비용이 상당히 증가하였으며, 이로 인해 경제적 문제 뿐만 아니라 안정성에 대한 문제도 발생하고 있다. 이러한 문제를 해결하기 위해 반잠수식 구조물, 시추선(Drill-ship), 부유식 원유생산, 저장 및 하역설비(Floating production storage offloading, FPSO) 등과 같은 부유식 또는 유연식 해양구조물의 수요가 증가하게 되었다(Jung, 1999; Patel, 1989).
유연식 해양구조물의 주요 장비는 직경에 비해 길이가 매우 긴 세장체로 구성되어 있으며, 현재 이에 대한 연구가 활발히 진행되고 있다. 세장체 구조물에는 심해역의 원유 탐사 및 생산에 사용되는 라이저(Riser), 계류선(Mooring line), 그리고 해양 온도차 발전설비(Ocean thermal energy conversion, OTEC)에서 사용되는 라이저 등 다양하다. 세장체 구조물은 파랑, 조류 등의 해상환경에 의한 환경 하중을 받으며, 또한, 부유체의 운동으로 인한 가진력을 받는다. 이로 인해 유연식 구조물은 흐름 방향(Inline) 응답과 흐름에 직각방향(Transverse) 응답이 발생하는 3차원 운동을 하게 된다(Chucheepsakkul et al., 1995; Park et al., 2002; Lee et al., 2013; Jung, 1999). 세장체의 동역학적 거동해석을 위해서는 실험적 연구가 동반되어야 한다. 그러나 세장형 구조물의 모형실험을 수행하는데 있어 기하학적, 동역학적 상사를 만족시키는 것은 매우 어렵기 때문에 다양한 실험 기법이 연구되고 있다(Hong and Koterayama, 2004; Hong et al., 2002).
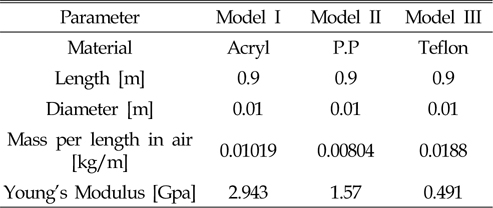
일반적으로 석유자원이나 가스 개발에 사용되는 라이저는 강관으로 구성되지만, 해양심층수를 취수하기 위한 라이저는 양질의 해양심층수를 공급할 수 있어야 하기 때문에 석유 및 가스를 운반하는 강관을 사용할 수 없고, 폴리에틸렌과 같은유연한 재질을 사용해야 한다. 사용 목적에 따라 여러 종류의 라이저를 사용해야 하는 유연식 해양구조물의 특성상 다양한 재질로 만들어진 세장체의 동역학적 거동 해석 및 해양구조물의 최적 설계에 관한 연구가 필요하다(Chen et al., 2009; Jung et al., 2004). 본 연구에서는 탄성 계수가 서로 다른 아크릴(Acryl), 폴리프로필렌(Polypropylene, P.P), 테플론(Teflon) 세 가지 재질로 모형 제작하여 강제동요, 규칙파, 균일류와 같은 다양한 외력환경 중 세장체의 흐름방향 및 횡방향 탄성응답을 분석하였다. 또한, 모형의 고유 주파수와 와류방출 주파수(Vortex shedding frequency)의 관계가 탄성응답에 미치는 영향을 분석하였다. 그 결과, 외력환경과 모형의 재질에 따라서 탄성응답의 크기가 다양하게 나타나는 것을 확인할 수 있었으며, 목표 해역의 해상상태에 적합한 재질을 이용하여 해양 구조물을 설계한다면 안정성 측면에서 많은 도움이 될 것으로 생각된다.
세장형 구조물을 설계 시, 목표 해역의 해상 상태를 고려하여 그에 따라 적절한 탄성을 갖는 재질을 사용하면 해양구조물을 가동하는데 있어 안정성과 경제성 측면에 있어 유리할 것으로 사료된다.
다양한 외력 환경 중 발생하는 세장형 구조물의 탄성응답 분석을 위해 모형의 고유 주파수를 이론 계산 값과 가진 실험을 통하여 얻은 데이터 값을 비교하였다. 실험에 사용된 세장체 모형의 1st mode 고유주파수는 식 (1)과 같다.
여기에서
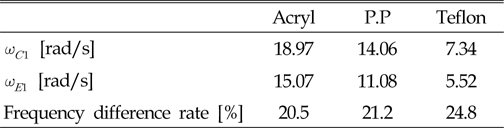
[Table 1] Natural frequency of models by theoretical calculations & experimental measurements
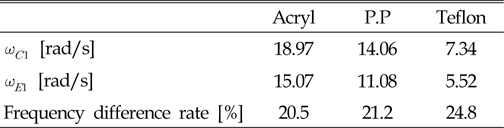
Natural frequency of models by theoretical calculations & experimental measurements
Vortex shedding 현상은 실린더형 구조물 주위 유동의 비대칭성에 의해 구조물의 후류에서 발생한 Vortex가 구조물로부터 떨어져 나가는 현상을 말한다. Vortex shedding에 의한 구조물의 진동 현상을 와유기 진동(Vortex induced vibration, VIV)이라 하며, 이는 유연식 해양구조물의 설계에 있어 매우 중요한 설계 인자이다.
Reynolds number(
본 연구에서의 실험조건 중
여기에서
Vortex shedding 현상을 분석하기 위해서는 Vortex shedding frequency를 파악할 필요가 있으며, Shedding frequency와 모형의 Natural frequency가 일치하거나 그의 배수가 될 때, 공진현상(Lock-in)이 발생하고, Vortex shedding frequency는 다음과 같다.
여기에서
본 실험은 한국해양대학교 해양시스템연구실 내에 위치한 2차원 조파수조 (25m(
실험에 사용된 강제동요장치는 종방향(X 방향), 횡방향(Y 방향), 상하방향(Z 방향), Rolling방향(
2차원 조파수조 내에 설치된 흐름발생장치의 유속은 최대 0.4m/s까지 생성할 수 있으며, 펌프 회전수를 제어함으로써 유속을 조정할 수 있다.
실험에 사용된 서보식 파고계는 수면 측정지점에 놓인 바늘 전극과 접지 전극이 접하고 있어 파고계와 파랑간 간섭이 없기 때문에 보다 정확한 파고를 계측할 수 있다.
유속 측정을 위해 Acoustic doppler velocimetry(ADV)를 사용하였고, 측정 가능한 유속 범위는 0.001~2.5m/s이며, 오차 범위는 ±1%이다.
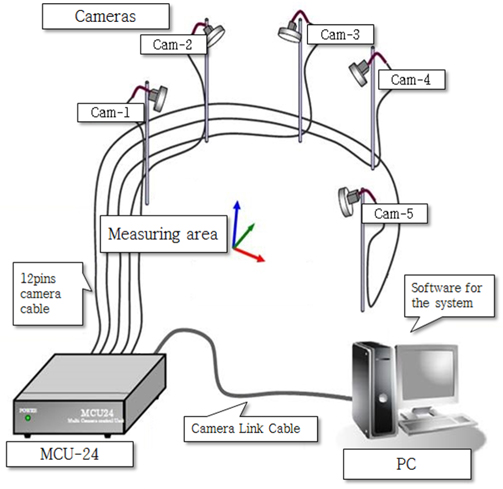
세장체 모형의 탄성응답 분석을 위해 일본의 ‘Ditect’사에서 제작된 3차원 운동계측 장비를 사용하였다. 광학적계를 이용한 이 장비는 실험 대상에 부착된 반사 마커의 운동을 5대의 CCD(Charge-coupled device)카메라가 실시간으로 계측 가능하도록 설정되어 있다. Fig. 5에서 볼 수 있듯이 각 카메라들과 연 결된 ‘MCU-24’장치는 카메라에서 계측된 정보를 종합하여 각 마커의 X, Y, Z축 변위 데이터를 PC로 전송한다. PC로 전송된 데이터에서 발생할 수 있는 반사 마커간의 오차와 교란현상의 보정을 위해 ‘DIPP-Motion’프로그램을 이용하였으며, 오차는 0.7mm 미만이다.
모형은 Fig. 6과 같이 두께 0.01m의 얇은 원반형 판과 세장체로 구성되고 서로 다른 탄성계수를 갖는 아크릴, 폴리프로필렌, 그리고 테플론 재질로 제작되었으며, 모형의 제원은 Table 2와 같다. 세장체에는 길이방향에 대해 0.04m 간격으로 반사테이프가 부착되었고, 얇은 비닐재질로 구성된 반사테이프를 이용함으로써 모형의 탄성 특성에 미치는 영향을 최대한 줄이고자 하였다. 반사체가 부착된 각 지점에 대한 변위를 계측하여 탄성응답을 분석하였다.
[Table 2] Characteristics of Models
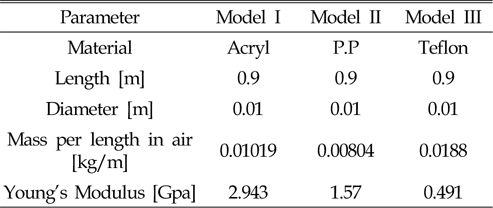
Characteristics of Models
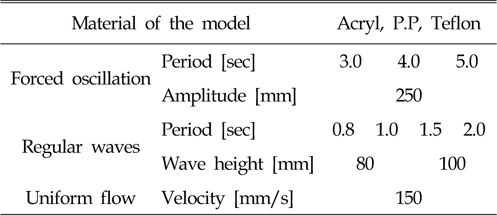
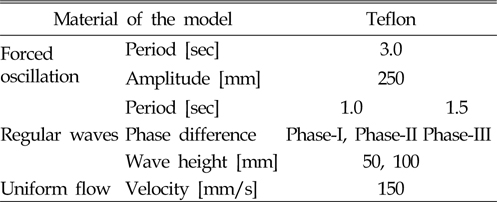
2차원 조파수조에서 탄성계수가 서로 다른 세장체 모형을 Fig. 7과 같이 강제동요장치에 고정시켜 놓은 상태에서 실험을 실시하였다. 실험은 강제동요, 규칙파, 균일류가 단일⋅합성된 외력조건에서 수행하였으며, 각각의 외력이 안정적으로 발생할 수 있는 조건하에서 실험을 실시하였다. 단일외력의 실험 환경은 Table 3과 같다.
[Table 3] Experimental conditions for a single external force
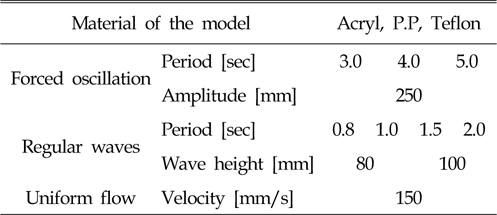
Experimental conditions for a single external force
모형의 각 지점에서의 변위데이터로 3차원 운동경향을 파악하고, 흐름방향(X방향)과 횡방향(Y방향)에 대한 탄성응답을 분석하였다. Fig. 8에 보이는 것처럼 모형 상단 및 하단에 부착된 Point 1과 13의 X축 방향 변위차이를 이용하여 흐름방향 탄성 응답을 분석하였다. 횡방향 탄성응답도 같은 방법으로 Y축 방향의 변위를 이용하여 나타내었다.
흐름방향 및 횡방향 탄성응답 분석을 수행하기 위해 여러 실험조건에 대한 모형의 3차원 변위 데이터를 계측하여 비교⋅분석하였다.
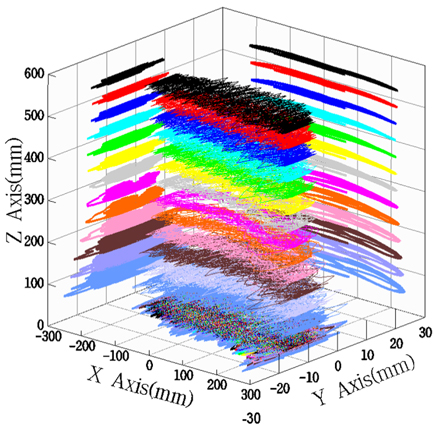
Fig. 9는 테플론 모형에 강제동요 주기 3.0sec, 진폭 250mm의 외력이 가해진 것에 대한 변위 그래프를 나타낸 것이다. 그래프는 모형에 부착된 반사체의 운동을 3차원적으로 보여주고 있다. 또 한, 이 운동을 XY, XZ, YZ면에 투영시켜 나타내었으며, 이를 이용하여 흐름방향 및 횡방향 응답을 분석하였다.
본 절에서는 아크릴, 폴리프로필렌, 테플론 모형에 강제동요, 규칙파와 균일류가 가해지는 각 조건들에 대한 모형의 흐름방향 및 횡방향 탄성응답을 분석하였다.
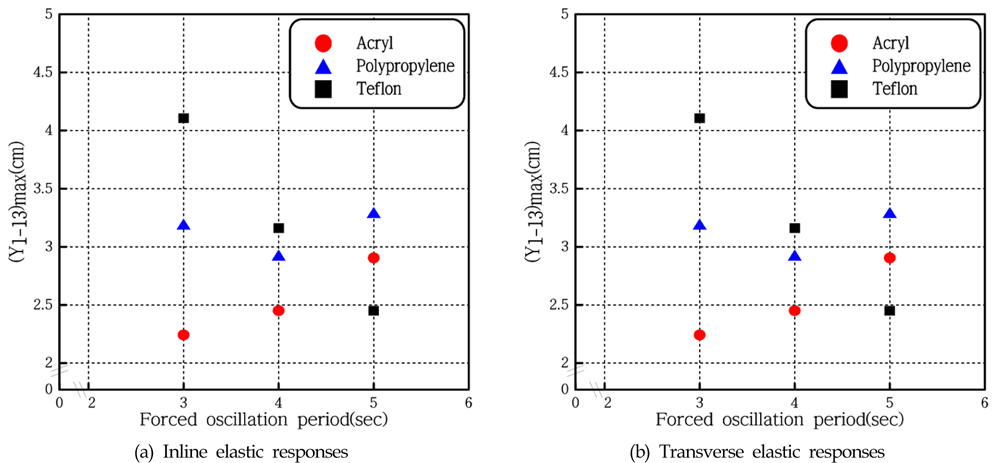
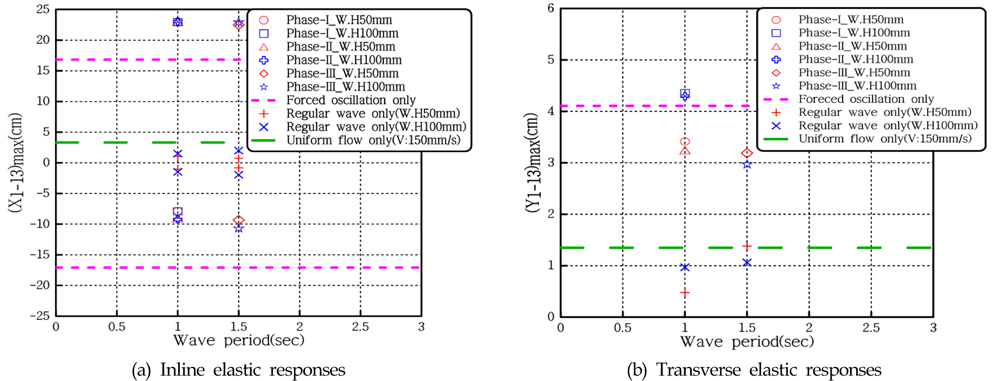
Fig. 10(a)는 강제동요에 대한 흐름방향 탄성응답을 나타낸 것으로 ‘+’방향과 ‘-’방향의 값이 상하 대칭되는 것을 볼 수 있고, 모형의 강성이 작고 강제동요 주기가 짧을 때, ±17cm 정도로 응답이 가장 크게 나타난다. Fig. 10(b)를 보면, 횡방향 응답은 강제동요 주기와 모형의 강성에 따라 다르게 나타나는 것을 볼 수 있다. 주기 3.0sec에서는 강성이 가장 작은 테플론 모형의 응답이 4.1cm로 가장 크게 나타나지만, 주기가 긴 5.0sec인 경우 중간 강성을 갖는 폴리프로필린 모형이 3.3cm로 제일 크게 나타난다.
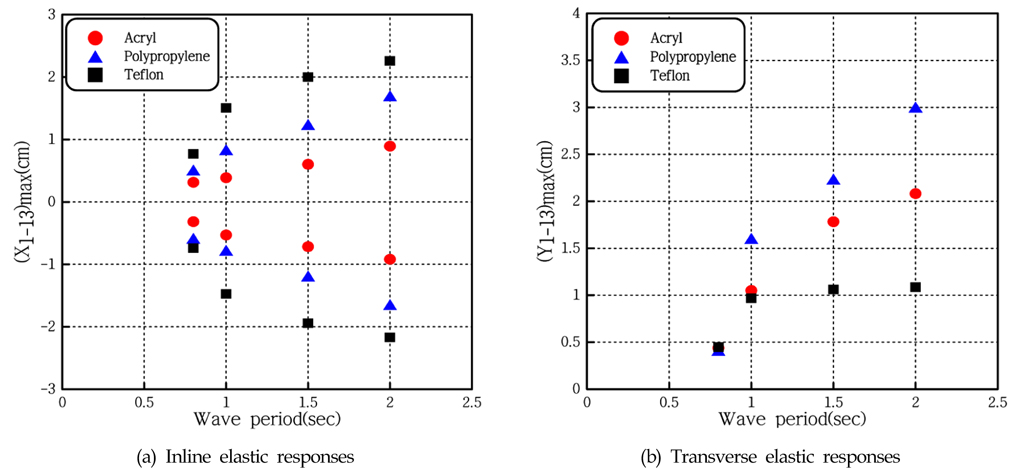
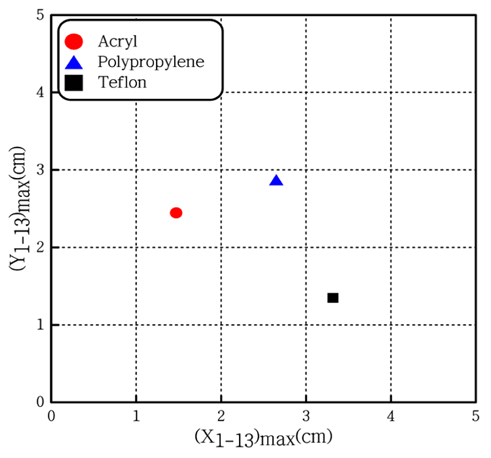
Fig. 11은 규칙파 중 탄성응답을 나타낸 것으로 Fig. 11(a)를 보면 주기가 길어지고 강성이 작을수록 흐름방향 탄성응답이 크게 나타난다. Fig. 11(b)의 횡방향 탄성응답은 주기가 길어지면 전체적으로 커지며, 모형별 재질에 따라서는 강성이 큰 아크릴 모형과 강성이 작은 테플론 모형보다 중간 강성을 갖는 폴리프로필렌 모형에서 최대 3cm로 가장 크게 나타나는 것을 확인할 수 있다.
Fig. 12는 균일류 조건에 대한 탄성응답 그래프이고, 그래프의 X축은 흐름방향, Y축은 횡방향 탄성응답을 의미한다. 그래프를 보면, 흐름방향 응답은 강성이 작을수록 증가하고, 횡방향 응답은 중간 강성을 갖는 폴리프로필렌 모형에서 크게 나타나는 것을 볼 수 있다.
단일 외력환경에 대한 탄성응답 분석결과, 모형의 탄성과 외력 조건에 따른 탄성응답이 다르게 나타나기 때문에 세장형 해양구조물을 설계할 때, 설치 해역의 외력환경에 따라 재질을 선정할 필요가 있다는 것을 알 수 있다.
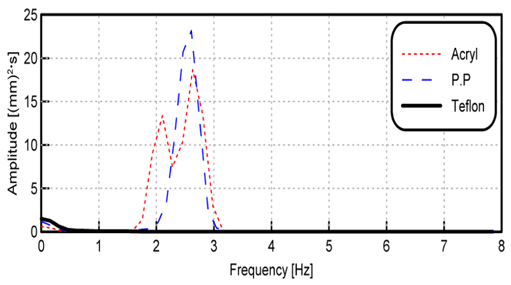
다음으로 균일류가 가해질 때 모형 제일 하단 지점인 Point 13의 횡방향 운동 데이터를 통해 얻은 Shedding frequency의 실험 값을 계산 값과 비교⋅검증하였다. 그리고 각 모형별로 발생하는 현상을 Fig. 13에 나타낸 것과 같이 주파수 영역 해석을 통해 분석하였다. 실험조건(Flow velocity: 150mm/s)에 대해 계산된 Shedding frequency는 약 3Hz이지만, 아크릴과 폴리프로필렌 모형의 경우, 실험을 통해 얻은 주파수는 약 2.7Hz로 계산값과 다소 차이가 있다. 하지만, 두 값의 오차는 약 8%로 실험적 오류를 고려하면 신뢰할 수 있다고 볼 수 있다. Fig. 13을 보면, 아크릴 모형은 두 지점에서 최대 값을 보이는데, 이는 강성이 커 횡방향 운동이 크게 나타나는 것과 모형의 고유주파주가 같이 맞물리면서 발생하는 것으로 보인다. 테플론 모형은 저주파수 영역에서 Shedding frequency가 나타났는데, 이는 강성이 작아 흐름방향의 운동이 횡방향 운동보다 상대적으로 커 장주기 운동을 유발하는 것으로 생각된다.
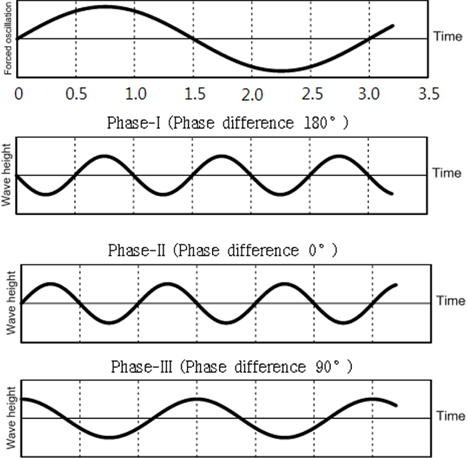
본 절에서는 실험환경의 한계 및 가장 유연한 재질의 응답특성을 중점적으로 보고자 테플론 모형을 이용하여 실험을 수행하였으며, 합성된 외력이 가해질 때 발생하는 모형의 흐름방향 및 횡방향 탄성응답을 분석하였다. 크게 3가지 경우에 대해 실험을 수행하였는데, 첫 번째는 강제동요와 규칙파가 합성된 경우, 두 번째는 규칙파와 균일류가 합성된 경우, 마지막 세 번째는 모든 외력이 합성된 조건이고, 그에 대한 외력조건은 Table 4와 같다. 강제동요와 규칙파가 합성된 경우에는 추가로 3가지 위상차를 주어 실험을 수행하였다.
[Table 4] Experimental conditions for synthesized external forces
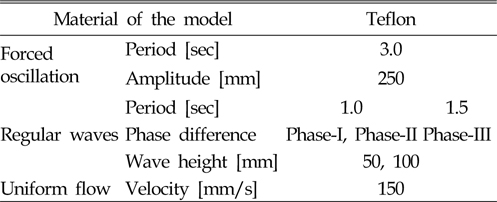
Experimental conditions for synthesized external forces
4.2.1 강제동요와 규칙파 중 탄성응답분석
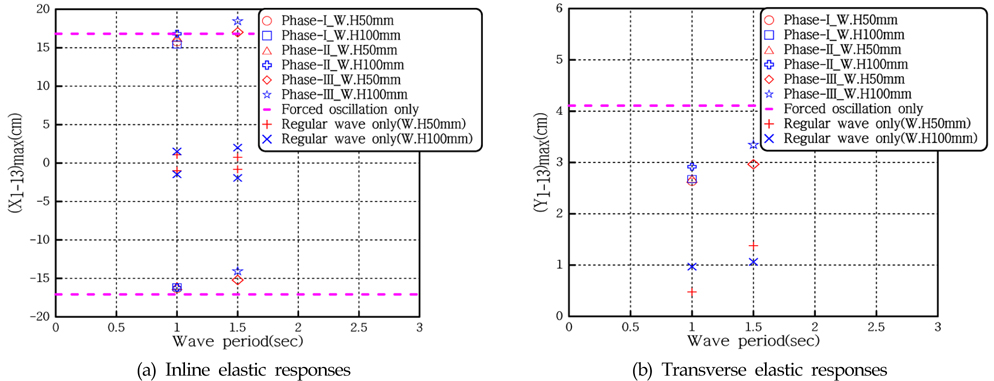
Fig. 15는 강제동요와 규칙파가 합성된 외력과 각 단일외력에 대한 탄성응답을 나타낸 그래프이고, 두 외력간의 위상차를 Fig. 14와 같이 3가지로 주어 위상차가 탄성응답에 미치는 영향을 파악하였다.
Fig. 15에서 짧은 점선은 단일 강제동요에 대한 응답, ‘+’와 ‘×’기호는 단일 규칙파의 응답을 의미하고, 나머지 기호들은 그래프에 나타나있는 바와 같다. Fig. 15에서와 같이 강제동요와 규칙파가 합성되면 위상에 따른 상호작용(Interaction)의 영향으로 ‘+’ 및 ‘-’방향 응답의 크기가 달라진다. Fig. 15(b)를 보면, 파주기 1.5sec에서는 파고가 커짐에 따라 응답이 3cm 가량 증가하는데, 이는 파랑에 의한 상호작용이 나타난다고 볼 수 있다. 하지만, 파주기 1.0sec에서는 파고의 증가에 따른 응답의 크기 변화가 많지 않기 때문에 파랑에 의해 탄성응답이 증가한다고 보기 어렵다. 그래서 두 외력이 조우하는 위상에 따라 상호작용이 달라질 수 있기 때문에 그에 대한 응답도 바뀔 수 있다. 외력이 합성된 경우에 대한 횡방향 탄성응답은 점선으로 표시된 단일 강제동요 응답의 크기보다 최대 1.5cm 정도 더 작게 나타나는데, 이는 두 외력간의 상호작용으로 인해 발생하는 것으로 볼 수 있다.
4.2.2 규칙파와 균일류 중 탄성응답분석
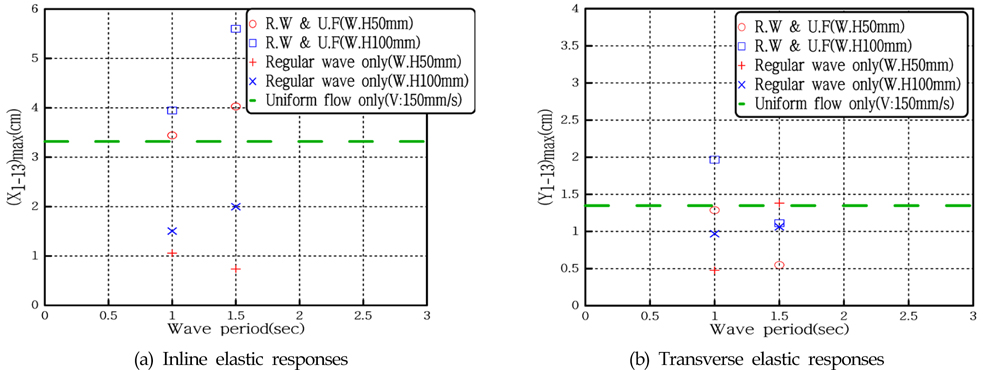
Fig. 16은 규칙파(Regular wave, R.W)와 균일류(Uniform flow, U.F)가 합성된 외력에 대한 흐름방향 및 횡방향 탄성응답 그래프이다. 그래프에서 원형과 사각형 기호는 합성외력에 대한 탄성응답을 나타내고, ‘+’와 ‘×’기호는 단일 규칙파의 응답, 긴 점선은 단일 균일류에 대한 응답을 의미한다. Fig. 16(a)를 보면, 합성외력에 대한 흐름방향 탄성응답은 파 주기가 길어지고 파고가 높아질수록 전체적인 응답이 커지며 최대 6cm 가까이 계측되었고, 이와 같은 경향은 두 외력간의 상호작용으로 인해 나타난다고 볼 수 있다. Fig. 16(b)에서 단일 규칙파만 가해진 경우의 횡방향 응답은 파주기가 길어짐에 따라 증가하는 양상이 나타나지만 균일류와 합성된 외력환경 하에서의 응답은 파주기가 짧고 파고가 높으면 커지는 것을 볼 수 있고, 이러한 현상은 두 외력의 상호작용으로 발생한다고 볼 수 있다. 즉, 단일 규칙파와 두 외력(R.W & U.F)이 합성된 경우에 대한 횡방향 탄성응답을 비교해보면 서로 다른 파랑 조건에서 탄성응답이 커지는 것을 알 수 있다. 따라서, 유연식 구조물을 설치하고자 하는 해역의 파랑환경과 중점을 두고자하는 응답을 고려하여 설계할 필요가 있다.
4.2.3 강제동요, 규칙파, 균일류 중 탄성응답분석
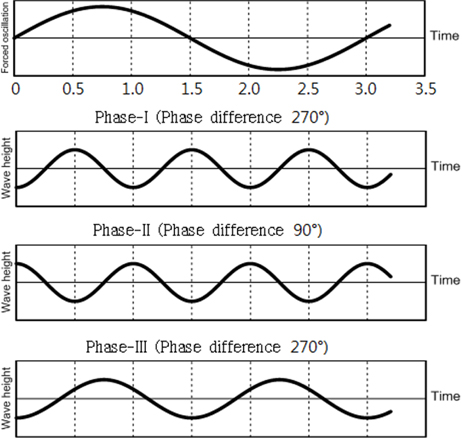
Fig. 18(a), (b)는 강제동요, 규칙파와 균일류가 합성된 외력환경에 대한 흐름방향 및 횡방향 탄성응답 그래프이고, 강제동요와 규칙파의 위상차를 Fig. 17과 같이 3가지로 주어 실험하였다.
Fig. 18에서 짧은 점선은 단일 강제동요에 대한 응답, ‘+’와 ‘×’ 기호는 단일 규칙파의 응답, 긴 점선은 단일 균일류에 대한 응답을 의미하고, 나머지 기호들은 그래프에 나타나있는 바와 같다. Fig. 18(a)에서 합성된 외력환경의 흐름방향 탄성응답을 보면, 세외력간의 상호작용으로 인해 파 주기와 파고간의 응답 차이는 크지않고, 그 응답은 +24cm에서 -10cm로 대부분 비슷하게 나타나는 것을 볼 수 있다. 그리고 이 응답은 각 외력에 대한 응답(‘+’, ‘×’, 점선 기호)이 선형 중첩되어 나타나는 것을 확인할 수 있다. Fig. 18(b)에서 합성 외력에 대한 횡방향 탄성응답은 세 외력들간의 상호작용으로 인해 전체적으로 작아지고, 흐름방향 응답과 달리 선형 중첩되는 경향이 나타나지 않는다.
본 논문에서는 다양한 외력환경 중 강성이 서로 다른 재질로 제작된 세장형 모형의 탄성응답을 비교⋅분석하였다.
(1) 단일 외력 환경에 대해 흐름방향의 탄성응답은 주로 모형의 강성이 작고, 외력의 주기가 길고, 운동 진폭이 클수록 증가하는 경향이 나타난다. 응답의 최대 값은 강제 동요주기 3.0sec의 경우에서 테플론 모형이 약 17cm 정도 발생하였고, 폴리프로필렌 모형은 10cm 그리고 아크릴 모형은 약 6cm로 계측되었다.
(2) 단일 외력 환경에 대해 횡방향 응답은 모형의 재질과 외력간의 공진관계 유무에 따라 크고 작게 발생한다. 여러 외력 환경 중 규칙파 조건에서 보면, 세 모형의 횡방향 탄성응답은 파주기 0.8sec에서 0.5cm로 비슷하게 나타났다. 그리고 파주기 2.0sec에서 폴리프로필렌 모형의 횡방향 응답은 3cm, 아크릴 모형은 약 2cm그리고 테플론 모형은 약 1cm가 발생하였다.
(3) 강제동요와 규칙파가 합성되면 흐름방향 응답은 외력의 상호작용에 의해 ‘+’방향으로 중첩되어 +15~19cm 정도로 나타나고, 합성된 외력에 대한 횡방향 탄성응답은 단일 강제동요 중 응답보다 1cm 가량 작은 +2.5~3.5cm가 발생하였다.
(4) 세 외력이 합성된 경우, 흐름방향 탄성응답은 선형 중첩되어 전체적으로 비슷하게 나타난다. 반면 횡방향 탄성응답은 외력간 상호작용으로 인해 불특정 조건에서 증가 및 감소하는 복합적인 현상이 나타나고 1cm 이상 차이가 발생한다.
(5) 세장형 구조물을 설계 시, 목표 해역의 해상 상태를 고려하여 그에 따라 적절한 탄성을 갖는 재질을 사용하면 해양구조물을 가동하는데 있어 안정성과 경제성 측면에 있어 유리할 것으로 사료된다.