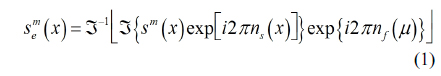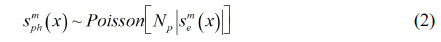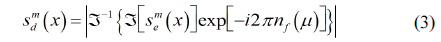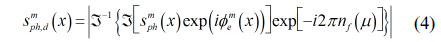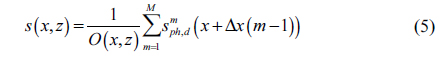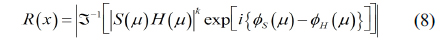Recently, data encryption techniques have been widely researched [1-11]. Double random phase encryption (DRPE) that is one optical encryption technique has many advantages; easy implementation and high encryption speed [5]. DRPE uses two independent random phase masks, which follow the statistical distribution such as Uniform distribution with support [0, 1] to encrypt the primary data. For decryption, it uses one random phase mask used in the encryption stage as the key information. Thus, if this key information is revealed, the security is destroyed. To enhance the security level of DRPE, a photon counting imaging technique has been applied [6, 7] that follows a Poisson distribution. Due to its sparseness for image sensing, attackers cannot recognize the decrypted data successfully. However, under severely photon-starved conditions, the primary data cannot be decrypted with the key information correctly. Therefore, to visualize and authenticate the primary information, three-dimensional (3D) imaging techniques such as integral imaging [12] and correlation filters [13, 14] can be utilized. In integral imaging, multiple images with different perspectives can be used for 3D reconstruction. In this paper, we use integral imaging and nonlinear maximum average correlation height (MACH) filter to obtain more accuracy of information authentication for optical encryption compared with a nonlinear correlation filter.

The paper is organized as follows. We present 3D photon counting DRPE concept and information authentication using nonlinear MACH filter in Section II. Then, we show the experimental results for proving our proposed method in Section III. Finally, we conclude our method with a summary in Section IV.

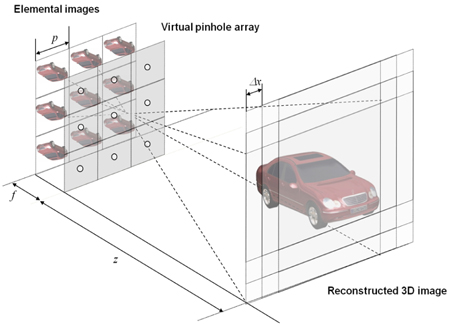
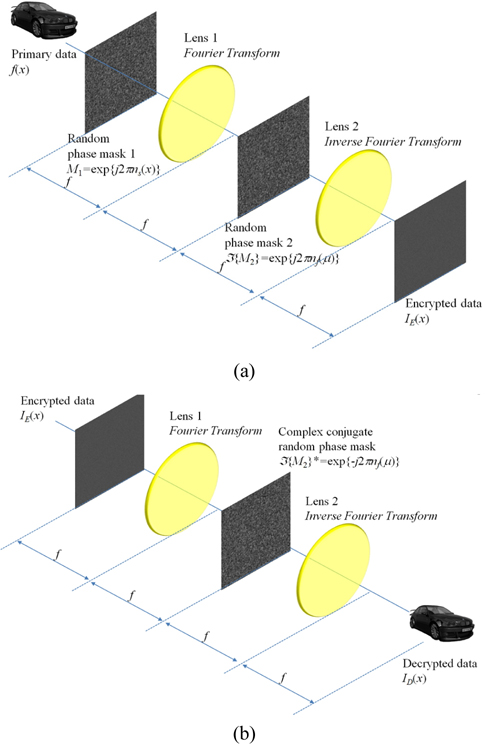
In photon counting DRPE, the decrypted data may not be authenticated well. To improve the information authentication, a 3D integral imaging technique can be applied because it uses multiple data to reconstruct 3D data as shown in Fig. 1. Therefore, this technique can be applied to DRPE as shown in Fig. 2. In this paper, for simple computation, we use one-dimensional notation only. The encryption process of DRPE can be described by the following:

where S^m(x) is the mth primary data of integral imaging, n_s(x) and n_f(μ) are random phase masks in spatial and spatial frequency domains, 𝔍 and 𝔍^-1 are Fourier transform and inverse Fourier transform, and S_e^m(x) is the mth encrypted data, respectively.

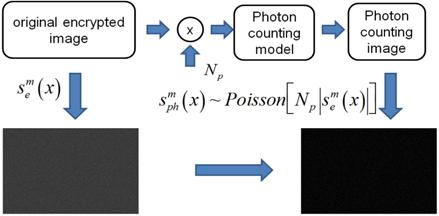
Now, we have the encrypted data for the primary data. To enhance the security level, we can apply the photon counting imaging technique to the amplitude component of the encrypted data. In general, the photon counting imaging technique can be utilized for detecting the information of objects in low light level environments. Its characteristic seems to be sparse detection. Thus, using sparse detection of the photon counting imaging technique, we can enhance the security level of optical encryption. Photon counting detection can be modeled by statistical distribution such as Poisson distribution since events of photons occur rarely in unit time and space [15]. Figure 3 illustrates the concept of photon counting detection using a statistical distribution. To extract photons from the original scene, Poisson random generation with the expected number of photons N_p can be used as shown in Fig. 3. In this paper, we apply computational photon counting detection to DRPE to enhance the security level. Therefore, photon-limited optical encryption can be implemented by the following:

where N_p is the expected number of photons (extracted number of photons from the image) and S_ph^m(x) is the mth encrypted data for photon counting DRPE, respectively. Also, conventional decryption process can be done by the following:

where S_d^m(x) is the mth decrypted data for conventional DRPE. Using the same manner, photon counting encrypted data can be decrypted by the following:

where S_ph,d^m(x) is the mth decrypted data for photon counting DRPE and ϕ_e^m(x) is the phase of the mth encrypted data, respectively. Using multiple photon counting decrypted data and computational reconstruction technique [7], 3D data can be obtained by the following:

where s(x, z) is the 3D reconstructed data at reconstruction depth z, O(x, z) is the superposition matrix for 3D reconstruction, Δx is the shifted pixels for 3D reconstruction, M is the index of images for integral imaging, N_x is the total number of pixels for each image, p is the pitch between image sensors, f is the focal length of the image sensor, and c_x is the size of the image sensor, respectively.

To authenticate the information, we need one particular filter design algorithm known as Maximum Average Correlation Height (MACH) filter [14], which has been found to be robust over a broad range of conditions such as variations in the object’s scale, its orientation, background clutter and noise. This filter uses many reconstructed 3D images at different reconstruction depths as the training data as shown in Fig. 4. In the Fourier domain, the MACH filter is given by the following:

where M(μ), D(μ), S(μ), and C(μ) are an average, power spectrum, and spectral variance of the training images and power spectrum of additive noise, α , β , and γ are parameters of MACH filter for the sharpness of correlation peak, the stability of the peak value in the presence of distortions, and the response to additive noise, respectively. To improve the performance of MACH filter, we introduce the kth-law nonlinear filter as the following:

R(x) is the correlation results with nonlinear MACH filter, k is the nonlinear coefficient with real number range (0, 1), respectively. Optimum k can be chosen by a performance metric for the correlation results such as peak sidelobe ratio (PSR). In addition, nonlinear MACH filter can help to improve the information authentication since the target object has 3D information. In other words, the MACH filter has many training data via various reconstruction depths and nonlinearity can improve the performance of correlation process, thus the nonlinear MACH filter is suitable for information authentication of 3D photon-limited DRPE.

Using Eq. (1) with primary image as shown in Fig. 5(a), the conventional encrypted image can be generated as shown in Fig. 5(b). The resolution of primary image is 1350(H)×1350(V) pixels. To obtain multiple 2D images with different perspectives, synthetic aperture integral imaging (SAII) is used. The camera array consists of 10(H)×10(V) cameras. The focal length of the camera is 50 mm. The distance between cameras is 2 mm. Perfectly decrypted image that is the same as Fig. 5(a) can be obtained using Eq. (3). Figure 5(c) shows a photon counting encrypted image using Eq. (2). We can notice that the pixel sparse exists in the image by adjusting N_p, because the total number of pixels for each image is 1,822,500 and the number of the extracted photons is about 1000. In other words, since the sparsity can enhance the security level of optical encryption, we set N_p=1000. Using Eq. (4), photon counting decrypted image can be achieved as shown in Fig. 5(d). Here, the decrypted image is not well recognized due to lack of photons. Figure 6 shows elemental images for true and false classes by SAII. True class has three objects with different depths. In addition, false class has three objects with different depths. Figure 7 illustrates 3D reconstruction results of true and false classes at various depths using Eqs. (5) and (6) with N_p=100000. As shown in Fig. 7, 3D objects can be revealed at the correct depths. However, because of severely photon-starved conditions, 3D objects cannot be recognized well by human eyes. Therefore, using Eqs. (7) and (8), information authentication can be implemented as shown in Fig. 8. Since conventional MACH filter with k = 1 is a linear correlation filter, the result is not perfectly sharp. On the other hand, the result using the MACH filter with 0 < k < 1 is sharper than the conventional one. It means that nonlinearity of the MACH filter can enhance the correlation result. We choose the optimum nonlinear coefficient k = 0.4 since the performance of the correlation such as peak sidelobe ratio (PSR) at z=340 mm is the best among others as shown in Fig. 9. As shown in Fig. 8 and 9, in case of false class, enough value of both correlation peak and PSR cannot be achieved. Therefore, we show that our proposed method can enhance the ability of information authentication for optical encryption by this experiment.

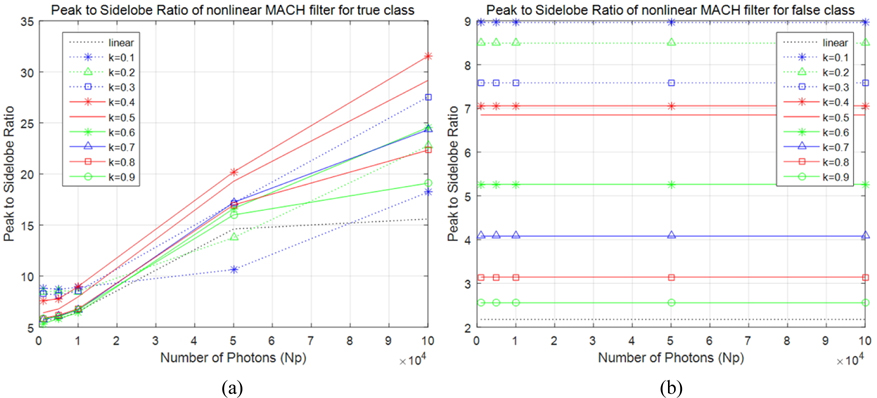
We have presented information authentication of 3D photon counting DRPE using a nonlinear MACH filter. In conventional DRPE, since the number of photons is sufficient for recognition, when attackers know the key information, the encrypted data can be decrypted easily. To avoid this attack, photon-limited DRPE can be utilized but the decrypted data may not be recognized well due to lack of photons. Thus, for information authentication, a nonlinear correlation filter may be used to enhance the recognition rate. However, in severely photon-starved conditions, nonlinear correlation filter may not obtain the better results. In addition, for 3D encrypted data, this correlation filter cannot recognize the information well because it is for 2D data. On the other hand, MACH filter can have the better performance for 3D data because it uses much training data with different depth information. In addition, to improve the information authentication, a nonlinear MACH filter can be used. Therefore, adjusting parameters of MACH filter and nonlinear coefficient k, the performance of correlation can be enhanced.