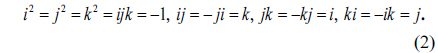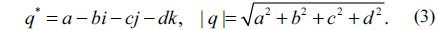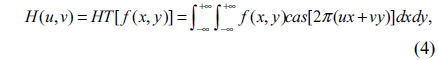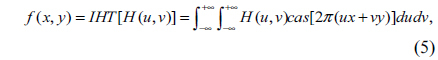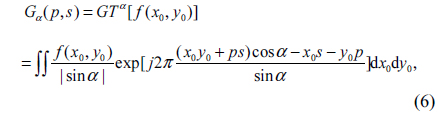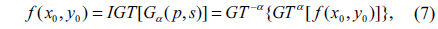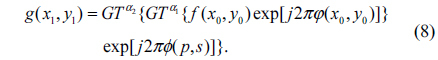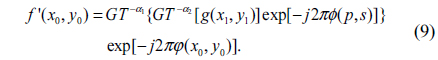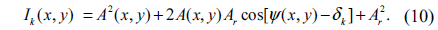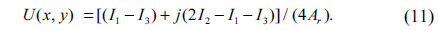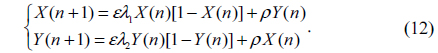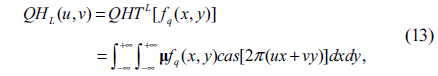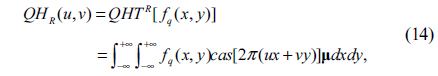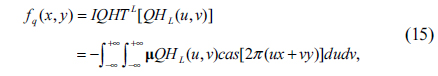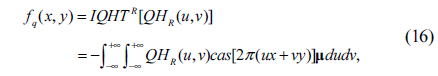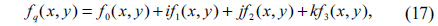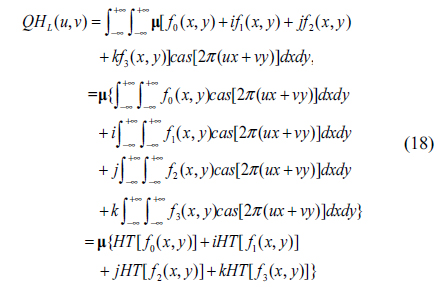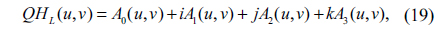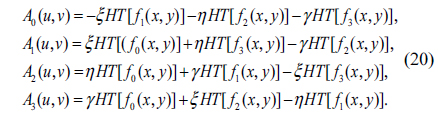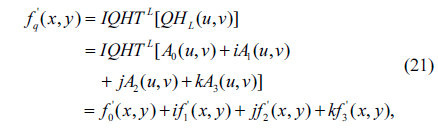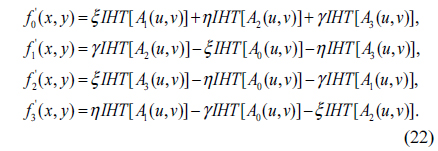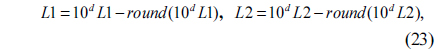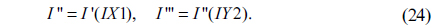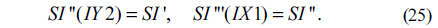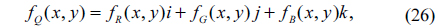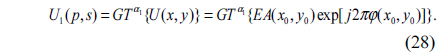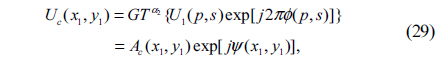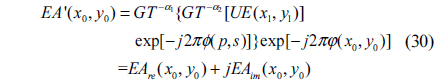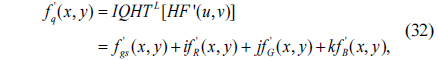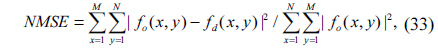Optical technology for security applications has received increasing interest in the last few decades [1-3]. In particular, the double random phase encoding (DRPE) [1] technique, in which the image is encoded to be a white noise pattern with two statistically independent random phase masks (RPM), has attracted much attention. The DRPE encryption technique is constructed by using two RPMs as keys: one is located at the input domain and the other is at the Fourier domain. To enlarge the key space, it has been further extended from the Fourier transform domain to the Fresnel transform domain [4, 5], the fractional Fourier transform domain [6], the Gyrator transform (GT) domain [7] and the Hartley transform (HT) domain [8], etc. In these encryption systems, the parameters (e.g. the propagation distance, the fractional order, etc) are introduced and served as extra keys. Since the HT is mathematically equivalent to the Fourier transform but is purely real, it has a computational advantage over the aforementioned transforms for not having to manage the real and imaginary parts [9]. Though most of the DRPE-based encryption techniques are quite robust and secure, the recovered image loses its color information, which is useful in image processing and practical applications, and in decryption since the original image is illuminated with monochromatic light [10].
Using the DRPE technique, Zhang and Karim reported a single-channel encryption algorithm for color image in the Fourier domain [11]. Chen et al. suggested a method using coherent diffractive imaging for optical color-image encryption and synthesis in the Fresnel domain [3]. Joshi et al. [12] have proposed an approach for the encryption of color images via using a fractional Fourier transform. By use of the Arnold transform and an interference method, a color image encryption technique is proposed in [13]. A method for securing color image based on the Arnold transform and the gyrator transform is reported in [10]. Based on polarization encoding, Nishchal et al. proposed two asymmetric color image cryptosystem techniques [14-15]. Li and Zhao [16] designed a color image encryption based on the fractional HT. However, the aforementioned encryption methods for color image ignore the potential interactions between different color channels [17, 18]. In these methods, a color image is separated into the three color channels, and encryption is carried out in each channel independently. Recently, quaternion theory [20] has been used in DRPE-based encryption. Based on the discrete quaternion Fourier transform (DQFT) and DRPE, a color image encryption method is reported [17]. With an iterative phase retrieval algorithm, an algorithm to encrypt double color images in quaternion gyrator domain is described [18]. Using quaternion representation, the color image is processed holistically as a vector field rather than as separated color components in both of the two methods. However, the method in [17] is vulnerable to some attacks (such as chosen-plaintext attack, etc) caused by the linearity of the cryptosystem, while the algorithm in [18] has high computational cost due to the phase retrieval iteration process.
In this paper, based on the quaternion Hartley transform (QHT), logistic-based scrambling technique, GT-based DRPE and three-step phase-shifting interferometry (PSI), a novel hybrid color and grayscale image encryption method is presented. In the proposed approach, the QHT is defined and its calculation for a quaternion matrix is developed first. Then a color image and a grayscale image are processed holistically in a vector manner using QHT. To resist an attack such as chosen plaintext attack, the components of the QHT-transformed images are permuted by use of the designed scrambling algorithm based on logistic maps. Since the flexible configuration of the GT based system, which means fixed distances between the generalized lenses and the manipulation of the transformation angle using lens rotation, makes the setup useful for image encryption [19], the GT-based DRPE technique is used to encrypt the images after QHT and permutation. The resulting encrypted signal from the cryptosystem is recorded as interferograms by the three-step PSI. Numerical simulations have been made for demonstrating the feasibility and performance of this encryption.
In this section, we come back to some related theories before extending the traditional HT to the quaternion domain, showing how to calculate the QHT of a quaternion matrix and developing the logistic maps-based scrambling technique, etc.
Quaternions can be viewed as generalizations of complex numbers. A quaternion number can be represented as follows [18]:
where a, b, c, and d are real numbers, and i, j, and k are three imaginary units obeying the following rules
The conjugate and modulus of a quaternion are respectively defined by
When a = 0, q is a pure quaternion.
In mathematics, the HT, which transforms real-valued functions to real-valued functions, is an integral transform closely related to the Fourier transform. HT has two main properties: one is that it is a real transform; the other is that it and its inverse transform are identical [21]. Therefore it can have computational advantages over the Fourier transform [21]. The HT [8] of a real function f(x,y) is defined as
and the inverse Hartley transform (IHT) is defined as
where cas = cos + sin, HT[•] and IHT[•] denote the Hartley and inverse Hartley operators.
In mathematics, the GT with respect to parameter α, called as a fractional order [7], of a two-dimensional function f(x,y) can be expressed as [7, 9]
where the Gα(p,s) and f(x0,y0) are the output and input of the transform, respectively. GTα [•] represents gyrator operator. The inverse GT (IGT) corresponds to the GT with respect to -α and is given by
where IGT[•] denotes the inverse gyrator operator. The GT can be achieved either by using an optical system [9] or by using a fast algorithm [22].
In Fig. 1, the optical setup of DRPE in the gyrator domain is shown. Three planes are defined as the input plane, the transform plane, and the output plane. The corresponding coordinates of the three planes are denoted by (x0,y0), (p,s) and (x1,y1), respectively. The two random phase masks RPM1 and RPM2 are represented by exp[j2πφ(x0,y0)] and exp[j2πϕ(p,s)], where φ(x0,y0) and ϕ(p,s) are two random functions distributed uniformly in the interval [0,1]. Using a system which is composed of three generalized lenses L1, L2 and L1 with fixed equal distances between them, the GT can be implemented optically. GT at order α is reached by rotation of these lenses [9]. In Fig. 1, the dashed block GT1 which contains lenses L1, L2 and L1 indicates the first optical GT with respect to α1, and the other GT2 containing lenses L'1, L'2 and L'1 indicates the second optical GT with respect to α2. When the security system is illuminated perpendicularly by a plane wave, the encrypted data g(x1, y1) is obtained at the output plane [9]:
By applying IGT to the encrypted data with the conjugates of the RPM1 and RPM2, the decrypted image can be obtained as follows [9]:
Since digital holography [2] provides a convenient form of recording the complex encrypted images after passing through the DRPE systems, phase-shifting interferometry is employed to record the complex resulting encrypted signal in the proposed scheme. A variety of PSI techniques have been developed, including three-step, four-step, etc [23].
Let A(x,y)exp[jψ(x,y)] and Arexp(jδk) be the complex amplitude distributions of the object wave in the recording plane and the reference wave in that plane at the kth exposure, respectively. Here, Ar is a constant, δk is the phase shift of the reference wave between two adjacent steps and k=1,2,…,N. The kth interference pattern Ik(x,y) can be represented as [24],
For a known set {δk}(k=1,2,...,N), a digital hologram U(x,y) can be derived as a function {Ik} and {δk}[24]. In the three-frame case, N is 3. When δ1=0, δ2=π/2 and δ3=π, a digital hologram U(x,y) from the three interferograms I1, I2 and I3 can be expressed as [24, 25]
Chaos theory is an evolutionary theory, which describes that the nonlinear dynamical systems change from ordered state to disordered state [26]. The dynamical systems are established based on various chaos functions such as logistic maps, which are extremely sensitive to the initial conditions. These functions generate iterative values which are completely random in nature. In this paper, the two-dimensional (2D) logistic map is used to make the change of sequence of image pixels. It is defined as [26]
The dynamic behavior of 2D logistic is controlled by the parameters ε, λ1, λ2 and ρ shown in Eq. (12). When ε =4, ρ=0.1, 0.65≤λ1≤0.9 and 0.65≤λ2≤0.9, the dynamical system is in a chaotic state and slight variations of the initial value will yield a drastically different result which is a non-periodic and non-converging sequence over time [26].
Due to the non-commutative multiplication property of quaternions, there are different types of QHT that can be defined. In this work, the left-side QHT (QHTL) and the right-side QHT (QHTR) are defined:
• Left-side QHT:
• Right-side QHT:
where fq(x,y) is a two-dimensional quaternion function and µ is a pure unit quaternion which meets the constraint that µ2 =-1. QHTL () and QHTR () are the left-side QHT and right-side QHT operations, respectively.
Corresponding to QHT, two forms of the inverse QHT (IQHT) are defined as follows
• Left-side IQHT (IQHTL):
• Right-side IQHT (IQHTR):
Here, IQHTL() and IQHTR() are the inverse left-side QHT and right-side QHT operations, respectively. QHT and IQHT are transformation pairs of each other. They ensure that a quaternion function fq(x,y) which is transformed into the QHT domain can be reconstructed completely by the inverse process without losing any information.
In this sub-section, the method which makes full use of the existing HT algorithm to calculate the QHT of a quaternion matrix is presented. Since the left-side QHT is used in this work, only the calculation method for it is described. By using the HT algorithm, the QHT can be implemented efficiently.
Since fq(x,y) is a quaternion function, it can be represented as
where f0(x,y), f1(x,y), f2(x,y) and f3(x,y) are real value functions.
For left-side QHT, substituting (17) into (13), we have
Considering the general unit pure quaternion µ= ξi + ηj +γk (ξ, η and γ are real numbers), substituting µ into (18) and using the properties of the quaternion shown in Eq. (2), we have
where
Similarly, applying left-side IQHT to Eq. (19), the reconstructed f’q(x,y) can be obtained.
where
It can be observed from formulas (18)~(22), the left-side QHT and IQHT of a quaternion matrix can be calculated effectively by using the traditional HT and IHT algorithms. Notice that the right-side QHT can be processed in a similar way.
By using a scrambling technique, He et al. claimed that an optical security system can resist some potential attacks such as chosen plaintext attack [27]. Since the dynamic response of the chaotic system is highly sensitive to the initial values and parameters of chaotic variables, and the chaotic trajectory is unpredictable, a 2D logistic map-based image scrambling technique is proposed to permute the position of image pixels.
Let I(m,n) be the to-be-permuted image. The scrambling method is described as follows
1) Calculate the height M and the width N of I(m,n).
2) Initialize X(1) and Y(1) randomly and choose an arbitrary natural number t first, then iteratively generate the chaotic sequences X(i) and Y(i) whose lengths both are MN+t by using Eq. (12). Here, i=1,2, …, MN+t.
3) Generate two integers s1 and s2 which are between 1 and t randomly first. In other words, 1≤s1≤t and 1≤s2 ≤t. Then truncate NM elements of X(i) from the s1th element to obtain a chaotic sequence L1={X(i), i=s1, s1+1,…, s1+MN-1}. Similarly, another chaotic sequence L2={Y(i), i= s2, s2+1,…, s2+MN-1} can be obtained by truncating from Y(i).
4) Compute the chaotic sequences L1 and L2 using the following equation
where round(Z) is the operation that rounds the elements of Z to the nearest integers, and d is an integer. After calculation, the irregularity and distribution uniformity of the sequences L1 and L2 can be enhanced, and all the elements of L1 and L2 are larger than -0.5 and less than 0.5 [28]. That is -0.5<L1<0.5 and -0.5<L2<0.5.
5) Sort the sequences L1 and L2 in a certain (ascending or descending) order to obtain two new sequence L’1 and L’2 and their corresponding permutation indices IX1 and IY2. In IX1 and IY2, there are MN elements respectively. The relations between L1 and L’1, and between L2 and L’2 are L’1=L1(IX1) and L’2=L2(IY2), respectively. For example, the mth element in L’1 corresponds to the IX1(m)th element in L1.
6) Map I(m,n) into a one-dimensional (1D) array I’ using the zigzag algorithm [29]. So the length of I’ is MN
7) Use the permutation indices IX1 and IY2 to permute I’ and the scrambled vector I''' can be obtained as follows
8) Finally, the scrambled image SI can be achieved by applying inverse zigzag scan [29] process to I '''.
The inverse image scrambling process is similar to the image scrambling process. In decryption (inverse scrambling process), obtain the permutation indices IX1 and IY2 as described in steps (1)~(5) with the same parameters first. Then map the scrambled image SI into a 1D vector SI’ using the zigzag algorithm. Subsequently, permute SI’ back to their original position using the following equations
Finally, the decrypted image DI can be retrieved by applying the inverse zigzag algorithm to SI '''. Since the proposed logistic-based scrambling method is highly sensitive to the parameters, including the initial values X(1) and Y(1), λ1, λ2, s1, and s2, it offers a huge level of security.
Let fRGB(x,y) be a color image with size M×N in the RGB color space. In principle, each image pixel of fRGB(x,y) can be treated as a pure quaternion number with real part equal to zero [17]:
where fR(x,y), fG(x,y), and fB(x,y) are the red, green and blue channels of fRGB(x,y), respectively. By using this representation, each color triple can be treated as a whole unit and be applied in encryption and watermarking [17, 18, 30]. Hence, a color image which is represented by a pure quaternion can be processed holistically in a vector manner using QHT. Furthermore, it should be noticed that a quaternion contains four parts, which results that more than a simple color image can be processed in encryption. For example, the real part of the quaternion matrix can be used to represent a grayscale image while the three imaginary parts represent a color image.
Therefore, based on the QHT, the scrambling method and the GT-based DRPE, a hybrid color and grayscale images encryption scheme is proposed. In the proposed method, the three step PSI is used to record the encrypted data. The optoelectronic setup of the proposed encryption process is shown in Fig. 2. Supposing fgs(x,y) denotes a grayscale image with size M×N, the proposed method is described as follows
1) Normalize fRGB(x,y) and fgs(x,y) first. To treat the color image and grayscale image in a holistic manner, fRGB(x,y) and fgs(x,y) are represented by quaternion: 1) Normalize fRGB(x,y) and fgs(x,y) first. To treat the color image and grayscale image in a holistic manner, fRGB(x,y) and fgs(x,y) are represented by quaternion:
fq(x,y) = fgs(x,y) + ifR(x,y) + ifG(x,y) + kfB(x,y) .
2) Apply QHTL to fq(x,y): HF(u,v)=QHTL[fq(x,y)]=A0(u,v) + iA1(u,v) + jA2(u,v) + jA2(u,v) + kA3(u,v) .
Here, QHTL () is the left-side QHT operation. A0, A1, A2 and A3 can be computed by using Eq. (20).
3) With A0, A1, A2 and A3, form a new matrix using the following formula.
Since the length and width of fRGB(x,y) and fgs(x,y) are both M×N, the size of AI is 2M×2N.
4) Permute AI to obtain AIS by the proposed chaos-based scrambling method mentioned in Section 4 with the parameters X(1), Y(1), λ1, λ2, s1 and s2. That is AIS = scramble(AI, X(1), Y(1), λ1, λ2, s1, s2). Here scramble() is the scrambling operation.
5) Let EA=AIS1+jAIS2, where AIS1=AIS[1:M, 1:2N] is the first half part of matrix AIS and AIS2=AIS[M+1:2M, 1:2N] is the second half part of AIS, respectively. EA can be regarded as the complex amplitude that will be encrypted by the DRPE technique in the gyrator domain. The size of EA is M×2N.
6) The complex amplitude EA is multiplied by RPM1, mathematically represented by function U(x0,y0) = EA(x0,y0) exp[j2πφ(x0,y0)].
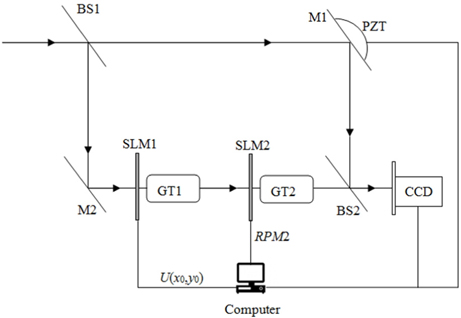
7) As shown in Fig. 2, import U(x0,y0) into the first spatial light modulator (SLM) SLM1 which is located in the input plane under the control of the computer, and then optically transformed by first GT at order α1. The resulting complex distribution U1(p,s) can be represented by
8) Subsequently, the complex function U1(p,s) is multiplied by RPM2 displayed on the SLM2 which is located in GT plane, and then optically transformed by second GT at order α2. So the object wave becomes
where Ac(x1,y1) and ψ(x1,y1) are the amplitude and the phase of Uc(x1,y1), respectively.
9) For convenience of storage and transmission, the object wave and reference wave overlap to produce real-valued interferograms. As shown in Fig. 2, the resulting encrypted data is recorded as three interference patterns I1, I2 and I3 in three-step PSI case mentioned in Sub-section 2.4.
In the encryption process mentioned above, the steps (1)~(6) will be performed digitally. In Fig. 2, M1, M2 are mirrors, and BS1 and BS2 are beam splitters. GT1 and GT2 are corresponding to the gyrator transform systems GT1 and GT2 shown in Fig. 1, respectively. As shown in Fig. 2, the complex function U(x0,y0) obtained in step (6) and the RPM2 are entered into the SLM1 and SLM2 respectively under the control of computer in order to be transformed, respectively. The phase shift δk (k=1, 2, 3) is introduced by a mirror attached with a Piezoelectric Transducer (PZT) controlled by a computer at the k exposure [31]. Finally, the resulting encrypted signal is captured and recorded as three interference patterns by a charge coupled device (CCD) which is placed at the output plane of the encryption system. The flowchart of the encryption process is shown in Fig. 3.
The parameters of the proposed encryption method, including X(1), Y(1), λ1, λ2, s1, s2, RPM1, RPM2 and the orders of GT α1 and α2, form a very large key space enhancing the security level of the encryption system. Only when all the right keys are simultaneously used for decryption can the encrypted data be reconstructed correctly.
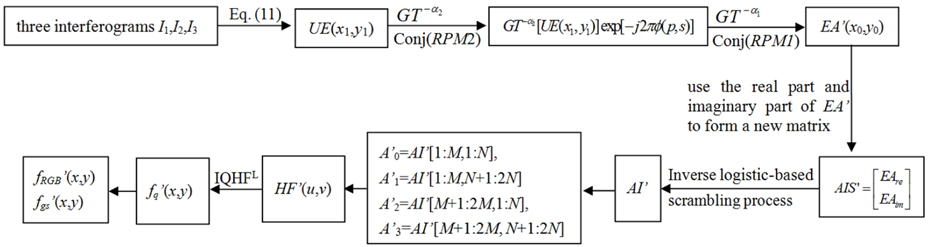
The decryption process, which is similar to the encryption process, but in the reversed order is depicted as follows:
1) Using the three interferograms I1, I2 and I3, an encrypted digital hologram UE(x1,y1) can be achieved using Eq. (11).
2) Apply a GT to UE(x1,y1) with order -α2 and then multiply the obtained complex distribution by the conjugate of the RPM2.
3) Make another GT with order -α1 and then multiply the achieved complex distribution by the conjugate of the RPM1. The resulting distribution function is as follows
where EAre(x0,y0) and EAim(x0,y0) are the real part and imaginary part of EA’ (x0,y0), respectively.
4) With EAre and EAim, form a new matrix using the following formula.
5) With the parameters X(1), Y(1), λ1, λ2, s1 and s2, AIS’ is permuted by the proposed inverse scrambling process mentioned in Section 4 to obtain AI’.
6) First, let A’0=AI’[1:M, 1:N], A’1=AI’[1:M, N+1:2N], A’2=AI’[M+1:2M, 1:N] and A’3=AI’[M+1:2M, N+1:2N]. Then let HF’(u,v)=A’0+iA’1(u,v)+jA’2(u,v)+kA’3(u,v).
7) Apply IQHT to HF’(u,v) to achieve f’q(x,y).
8) With the normalized f’R(x,y), f’G(x,y) and f’B(x,y), the decrypted color image f’RGB(x,y) can be obtained and the normalized f’gs(x,y) is the decrypted grayscale image.
Figure 4 depicts the decryption process. In Fig. 4, conj(RPM2) and conj(RPM1) are the conjugate of RPM2 and the conjugate of RPM1, respectively.
To verify the feasibility of the proposed encryption technique, numerical simulations are performed on the color image “Peppers” and the grayscale image “Lena”, which sizes are both 512×512, shown in Fig. 5(a) and Fig. 4(b). We carried out tests on a notebook computer with Intel(R) Core(TM) i7-4700HQ CPU @ 2.40GHz and 8G DDRL3 and with the MATLAB R2013a. In the experiments, the system parameters are µ=(i+j+k)/31/2, α1=0.92, α2=0.75, ε=4, ρ=0.1, X(1) = 0.24, Y(1) = 0.67, t=50000, λ1=0.716, λ2=0.881, s1= 12345, s2= 36578 and d=4. To evaluate the performance of image reconstruction quantitatively, the normalized mean square error (NMSE) [18] was used to calculate the similarity between the decrypted image and the original image, which is expressed as
where, fo(x,y) and fd(x,y) are the normalized original and the decrypted images respectively, and M×N is the size of the images.
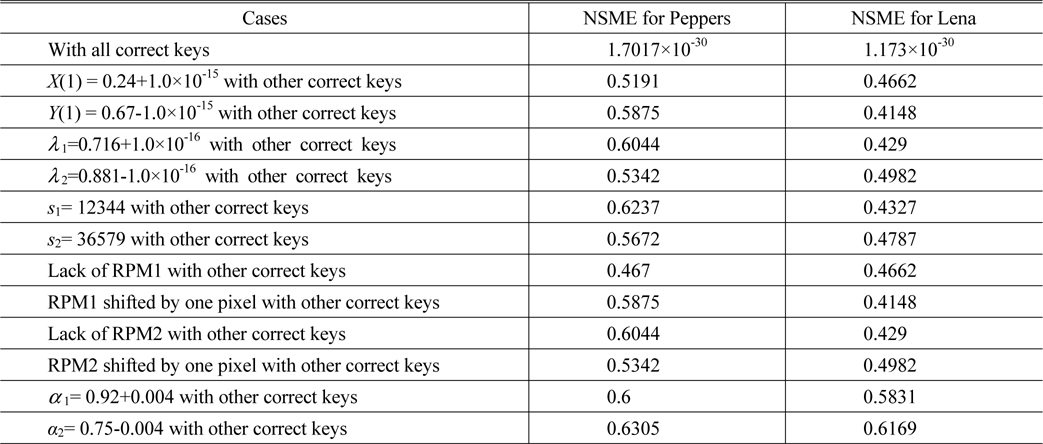
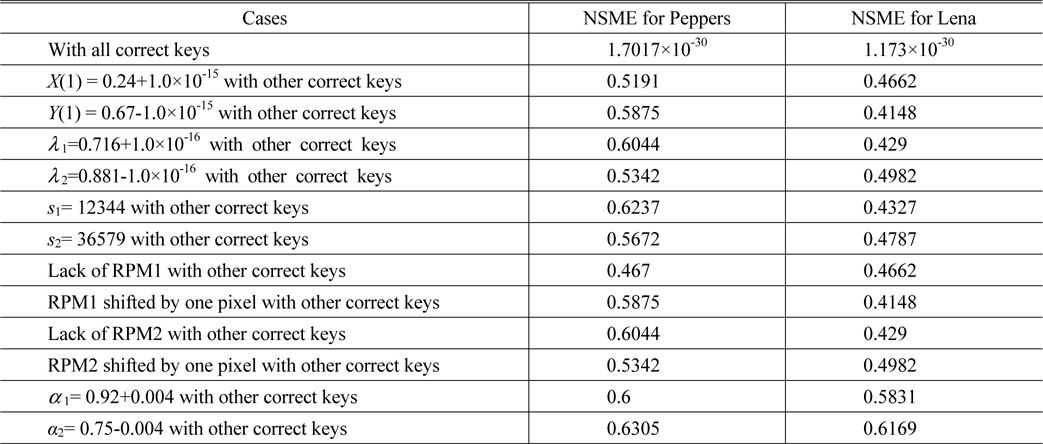
Using the proposed encryption scheme, the “Peppers” and “Lena” are encrypted and three encrypted interferograms are obtained, which are shown in Figs. 5(c)~5(e). Figs. 5(f)~5(g) display the retrieved color and grayscale images with the correct keys respectively, which are perfect, without any noise or distortion. As shown in Table 1, the NMSE between Fig. 5(a) and Fig. 5(f) and that between Fig. 5(b) and Fig. 5(g) are 1.7017×10-30 and 1.173×10-30, respectively.
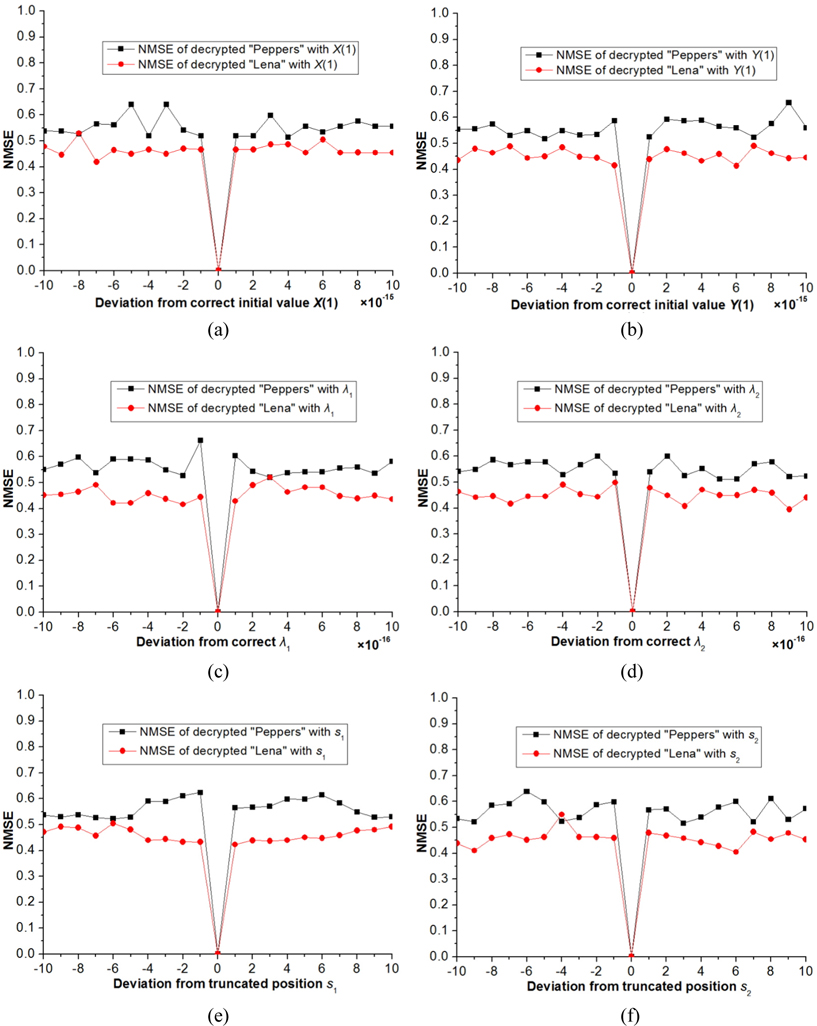
Now we investigate the sensitivity of retrieved image to small change of the parameters of 2D logistic map-based scrambling technique on the decrypted results. Figure 6 showed the derivation of NMSE versus the parameters X(1), Y(1), λ1, λ2, s1 and s2, respectively. Figs. 7(a)~7(l) show the decrypted color and grayscale images with wrong keys X(1)=0.24+1.0×10-15, Y(1)=0.67-1.0×10-15, λ1=0.716 +1.0×10-16, λ2=0.881-1.0×10-16, s1= 12344 and s2= 36579, respectively.
The corresponding NMSEs are listed in the upper part of Table 1. Please note that in the above experiments, the other keys remain correct while a key is changed in decryption. As illustrated in Figs. 6(a)~6(d) and Figs. 7(a)~7(h), we cannot obtain any information from the decryption images visually when the absolute values of deviations of X(1) and Y(1) are up to 10-15 and those of λ1 and λ2 are up to 10-16. In addition, we know from Figs. 6(e)~6(f) and Figs. 7(i)~7(l) that if the parameters s1 and s2 are less 1 or more 1 than the correct value, the decrypted images cannot afford any valid information. From the NMSE values shown in Table 1, it can also be concluded that the decrypted images cannot be recognized even if the keys of the scrambling system are changed slightly. So, the parameters X(1), Y(1), λ1, λ2, s1 and s2 are highly sensitive to the proposed method.
In the experiments, one of the two RPMs was removed or just one of them was shifted transversely by one pixel. The NMSE values of the decrypted images are listed in the middle part of Table 1. Figs. 8(a)~8(b) display the decrypted color and grayscale images, which are totally unrecognizable, with other correct keys but without RPM1. The recovered color and grayscale images, which were obtained from RPM1 shifted transversely by one pixel, are shown in Figs. 8(c)~8(d). These two images cannot be recognized too. The lack of the RPM2 or small changes to RPM2 in the decryption step also leads to similar results which are exhibited in Figs. 8(e)~8(h). Experimental results convincingly demonstrate that both RPMs are necessary in decryption and that the illegal users cannot access the security system without the RPMs.
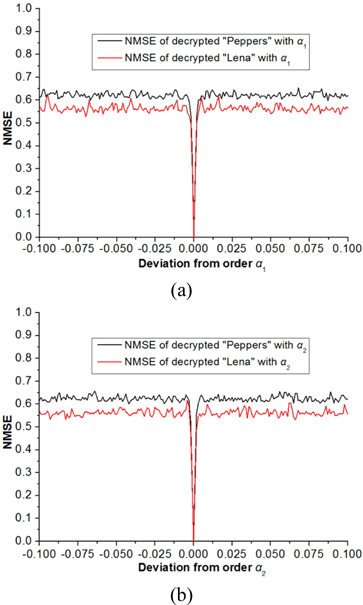
To examine the sensitivity of small change of the orders of the GT, the decryption processes are performed by fixing one order and varying the other. The relationship curves between the NMSE and the deviation of the GT order are shown in Fig. 9, in which the deviation ranges from -0.1 to 0.1 and the step is 0.001. As can be seen from Fig. 9, the NMSE value approximates to zero when α1 or α2 is correct while the value sharply increases when α1 or α2 slightly departs from the correct value, which indicates that any tiny fluctuation will result in false decryption. The NMSE values shown in the lower part of Table 1 also indicate that if the orders of inverse GT are changed by 0.004 from their correct values, the decrypted images are noise-like images as displayed in Fig. 10 and cannot be recognized.
Next we estimate the key space of the proposed encryption scheme. According to the description of the proposed method, we know that the key space of the cryptosystem consists of the RPMs, the orders of GT and the parameters of 2D logistic map. In addition, the chaotic permutation module is independent from the GT-based DRPE system. In the logistic-based permutation process, the key spaces of the parameters X(1), Y(1), λ1, λ2, s1 and s2 should be analyzed, which are denoted by Z1, Z2, Z3, Z4, Z5 and Z6, respectively. In the GT-based DRPE system, the key spaces of RPM1, RPM2 and the orders α1 and α,2, should be analyzed, which are denoted by Z7, Z8, Z9 and Z10 respectively. From Figs. 6(a)~6(d) and Figs. 7(a)~7(h), the parameters X(1), Y(1), λ1 and λ2 maintain 15, 15, 16 and 16 digits after decimal point respectively, so Z1×Z2×Z3×Z4=1062. Since 1≤s1≤t and 1≤s2≤t, Z5×Z6=t2 . Therefore, Z1×Z2×Z3×Z4×Z5×Z6=t2×1062. In our experiments, Z1×Z2×Z3×Z4×Z5×Z6=2.5×1071 since t=50000. Suppose that 256 levels are chosen for a pixel in initial random functions φ(x0,y0) and ϕ(p,s) of RPM1 and RPM2, the two RPMs with size of M×2N need to be decoded with 2×256M×2N attempts. In this case, M=N=512, so Z7×Z8 =2×256512×1024. Considering the sensitivity to one GT order of encryption system is 0.004, the fractional orders α1 and α2 can be varied with steps of 0.001 in fractional orders range [0, 1] [7], which results in Z9×Z10=(1/0.001)2 =106. Therefore, the entire key space of the cryptosystem is Z1×Z2×Z3×Z4×Z5×Z6×Z7×Z8×Z9×Z10=5×256512×1024×1077≈ 256512×1024×2258. As stated in [32], to acquire a high level of security, the size of key space should at least be larger than 2100. It is apparent that the key space of the proposed encryption system is far larger than 2100 and enormous enough to resist brute force attack.
Information loss or noise contamination may occur during data transmission. Now, the robustness of this scheme against occlusion attack which is regarded as data loss is tested. Figure 11(a) shows one of the interferograms occluded by 50%. The recovered images obtained with all correct keys are illustrated in Figs. 11(b)~11(c). It’s well known that Gaussian noise [33] and salt & pepper noise [33] are frequently appearing noises during the information transmission. The robustness test is further verified against noise attacks on the encrypted results. Figure 12(a) is one of the interferograms distorted by Gaussian noise with mean value 0 and standard deviation 20. The corresponding retrieved images are displayed in Figs. 12(b)~12(c). Fig. 12(d) exhibits one of the interferograms damaged by salt & pepper noise with density 0.02 added. Figs. 12(e)~12(f) depicts the corresponding retrieved images. Although all the results shown in Figs. 11(b)~11(c), Figs. 12(b)~12(c) and Figs. 12(e)~12(f) are interfered with seriously by noise and the corresponding NMSEs are big, the secret images among the noise fluctuation can still be distinguished.
Four attacks, including cipher only attack, known plaintext attack, chosen plaintext attack and chosen ciphertext attack [32], are often used to attack the DRPE-based optical security system to recover the ciphered images. Among these attacks, the chosen-plaintext attack is the most powerful attack [32]. He et al. claimed that permutation techniques can prevent the attacker from accessing the ciphertext obtained from the DRPE system in such attacks [27]. In addition, Zhang and Xiao stated that the security system should resist other attacks if it can resist chosen plaintext attack [32]. For the proposed method, we assume that the attacker has acquired the GT orders α1 and α2 of the GT-based DRPE system but does not know the parameters of the logistic-based scrambling algorithm. Using two fake color and gray images as the plaintexts, the two random phase masks of the proposed method can be produced by utilizing the chosen plaintext attack described in [34]. By use of these achieved keys, the attacker can crack the original ciphertext. Two keys RPM1’ and RPM2’ are generated by choosing Figs. 13(a)-13(b) as the fake plaintext images and then employed to decrypt the ciphertext of “Peppers” and “Lena”. As shown in Figs. 13(c)~13(d), the retrieved images cannot reveal any information visually. Therefore, the robustness against chosen-ciphertext attack is greatly enhanced because of the suggested logistic-based scrambling technique, which strengthens the nonlinearity in QHT domain. According to [32], the proposed encryption approach can also resist the other attacks mentioned above.
In the numerical simulation, the encrypted results were obtained by computer. So the computational complexity of the proposed encryption technique is calculated. The calculation depends on three main factors. First, to deal with a color image and a grayscale image holistically in a vector manner, the QHT is computed one time. According to the developed calculation method in sub-section 3.2, the QHT can be implemented via calculating HT four times. For an image with size M×N, the cost to compute the HT is O(MIN log2 MN) [35]. Hence, the complexity of QHT calculation is O(4MIN log2 MN). Second, to scramble a matrix using the proposed chaos-based technique, the 2D logistic map operation, the round operation, the quicksort algorithm [36], the zigzag scan operation, the inverse zigzag scan operation and the sequence permutation operation are performed one time, two times, two times, one time, one time and one time, respectively. As shown in the steps (3) and (4) of the proposed encryption method, the size of the to-be-scrambled matrix AI is 2M×2N though the sizes of the color image and grayscale image are both M×N. Therefore, the computational cost of the scrambling procedure is O(2(4MN + t) + 2(4MN + t) + 2(4MN + t)log2(4MN + t)) + (4MN + t) + (4MN + t) + (4MN + t). Here, t is the natural number shown in step (2) of the proposed scrambling method. Since 4MN + t ≈4MN and log2(4MN + t )≈2+log2 MN as MN tends to infinity, the complexity of the scrambling procedure is O(8MN log2 MN + 44MN). The last factor is the complexity of the virtual optical encryption process. In the proposed encryption method, an encrypted interferogram can be obtained after the complex amplitude being modulated two times by use of random phase masks RPM1 and RPM2, transformed two times by use of GT and interfered one time by use of the reference wave. For a matrix with size M×N, the complexities of GT operation, modulation operation and interference operation are O(2MN log2 MN) [22], O(MN) [37] and O(4MN) [37], respectively. Because the size of complex amplitude is M×2N, the computational cost of the above process is O(3(8MN log2 2MN + 4MN + 8MN)) = O(24MN log2 MN + 60MN). Thus, the total computational complexity of the proposed encryption scheme is O(36MN log2 MN +104MN). Since O(MN log2 MN) > O(MN), compared with the quaternion gyrator transform-based image encryption method whose computational complexity is O(4000MN log2 MN) [18], the proposed scheme is more efficient. In the experiments, the execution time for the encrypted results is 6.7728 seconds.
In the paper, a novel definition of quaternion Hartley transform and its implementation are presented first. Then a new method for hybrid color and grayscale images encryption is proposed, in which the QHT combined with the developed chaos-based pixel scrambling technique, the GT-based DRPE and the three-step PSI is used to encrypt the color and grayscale images. By use of QHT, a color image and a grayscale image are processed holistically in a vector manner without separating the color image into three channels and manipulating the grayscale image independently, so that the complexity of the security system can be reduced effectively without any reduction of its security. The components of the QHT-transformed original images are combined as the complex amplitude which will be strengthened the nonlinearity by the designed chaos-based scrambling technique and encrypted by the GT-based DRPE technique. In addition, the encrypted interferograms which are recorded by three-step PSI are real-valued, so they are convenient for storage and transmission. One needs to specify all the right keys to recover the original images correctly. Simulation results demonstrate that the proposed scheme has a quite sensitivity to the decryption keys, a enormous key space to resist brute force attack and a good robustness against Gaussian noise, salt & pepper noise and some attacks such as chosen plaintext attack.