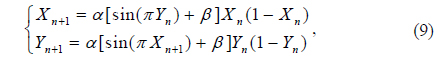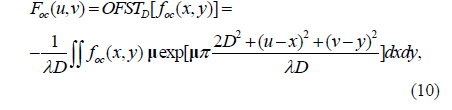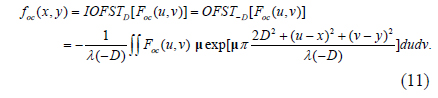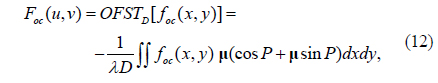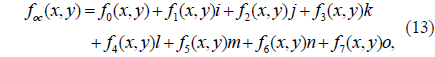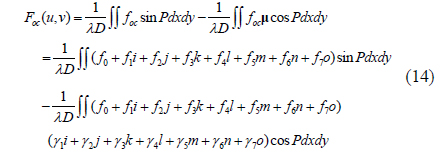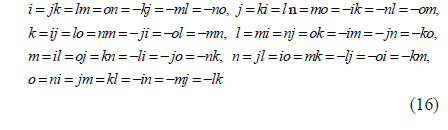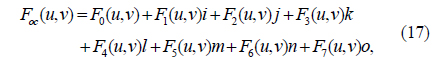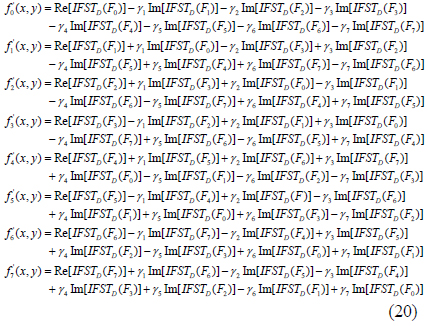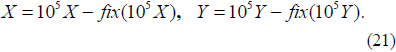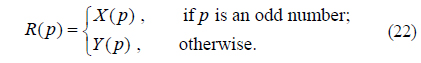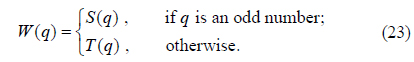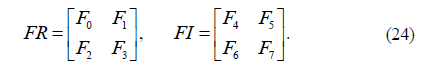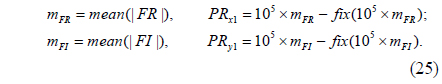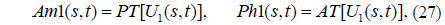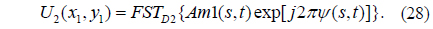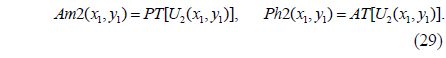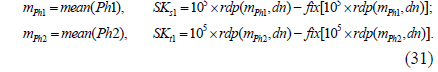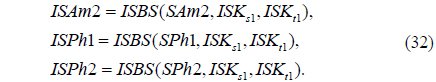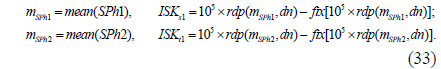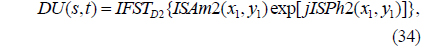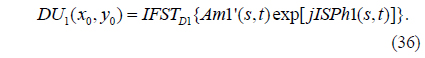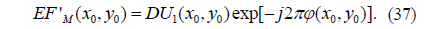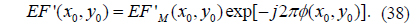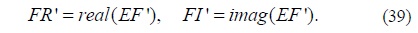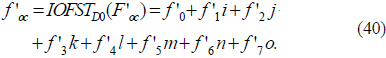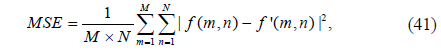Over the past two decades, optical image encryption techniques have played an important role in the information security field. Since development of the double random phase encryption (DRPE) technique [1], in which the image is encoded to be a white noise pattern with two statistically independent random phase masks (RPM), a number of improved DPRE-based image encryption methods have been proposed, to achieve higher security [2-7]. Most of the optical encryption methods can be viewed as symmetric cryptosystems, in which the keys for encryption and decryption are identical [8]. However, earlier studies indicated that these cryptosystems are lacking in security strength, because of the inherently linear property of mathematical or optical transformation, and are vulnerable to various attacks such as chosen plaintext attack [8-11]. In addition, most schemes mainly focused on single-image encryption, which leads to deficiency in multiple-image encryption and transmission [8].
To avoid the problems that arise from the linearity and symmetry of DRPE, an asymmetric encryption scheme based on phase truncated Fourier transforms has also been proposed [12], in which the encryption keys (public keys) are different from the decryption keys (private keys). However, when RPMs are used as public keys to encrypt different plaintexts, this method is still vulnerable to specific attacks such as known public key attack [13, 14]. To enhance security, it has been further extended from the Fourier transform (FT) domain to the Fresnel transform (FST) domain [15], the fractional Fourier transform (FrFT) domain [8], the Gyrator transform (GT) domain [11, 16], etc. To improve the efficiency of image transmission and communication over a network, more and more multiple-image encryption methods have been proposed [17-21]. Situ and Zhang reported the wavelength multiplexing-based multiple-image encryption scheme [16]. Using DRPE and an orthogonal encoding technique, Lee and Cho presented a multiple-image encryption method [18]. Based on the nonlinear amplitude-truncation (AT) and phase-truncation (PT) operations in the FT domain, Wang and Zhao developed an asymmetric multiple-image encryption scheme [19]. Based on coupled logistic maps and an iterative phase-retrieval process, Sui et al. introduced an asymmetric multiple-image encryption technique in the FrFT domain [20], but it has a high computational cost due to its iterative phase-retrieval process. Abuturab designed a multiple-color-image security system based on a generalized Arnold map in the GT domain [21]. However, the plaintexts in most multiple-image encryption methods are manipulated independently, resulting in complicated systems. Additionally, the increase in keys, such as the whole RPMs that have to be sent to the receiver side for decryption, in the aforementioned DRPE-based encryption schemes make it difficult to save and distribute the keys expediently and safely [22-23].
In this paper, based on the octonion Fresnel transform (OFST) and two-dimensional Sine Logistic modulation map (2D-SLMM), a novel asymmetric multiple-image encryption method is presented. In the proposed approach, first the OFST is defined and its calculation for an octonion matrix is developed. Then multiple images are processed holistically in a vectorial manner using OFST. Subsequently, the components of the OFST-transformed images are combined to construct the input complex amplitude. To improve robustness against attacks, the input information is modulated by a phase mask, which is generated based on 2D-SLMM. The initial values of the SLMM, which is computed using the components of the OFST-transformed images, are used as decryption keys. With AT, PT, and RPMs, the complex amplitude is encrypted in the Fresnel domain, and two decryption keys are produced in the encryption process. To enhance security, the encrypted result and two decryption keys are permuted by the proposed SLMM-based scrambling method. During decryption, the eight original grayscale images can be recovered with the correct encryption and decryption keys. Numerical simulations are presented to demonstrate the feasibility and performance of this encryption.
In this section, we discuss some related theories before extending the traditional FST to the octonion domain, showing how to calculate the OFST of an octonion matrix, and designing the 2D-SLMM-based scrambling technique, etc.
Octonions can be viewed as octets (or 8-tuples) of real numbers [24] and have been applied in image processing, such as image saliency detection [25]. An octonion can be represented as follows [24, 25]:
where ζ0, ζ1, ζ2, ζ3, ζ4, ζ5, ζ6, and ζ7 are real numbers, and i, j, k, l, m, n and o are seven imaginary units which satisfy the following rules [24]
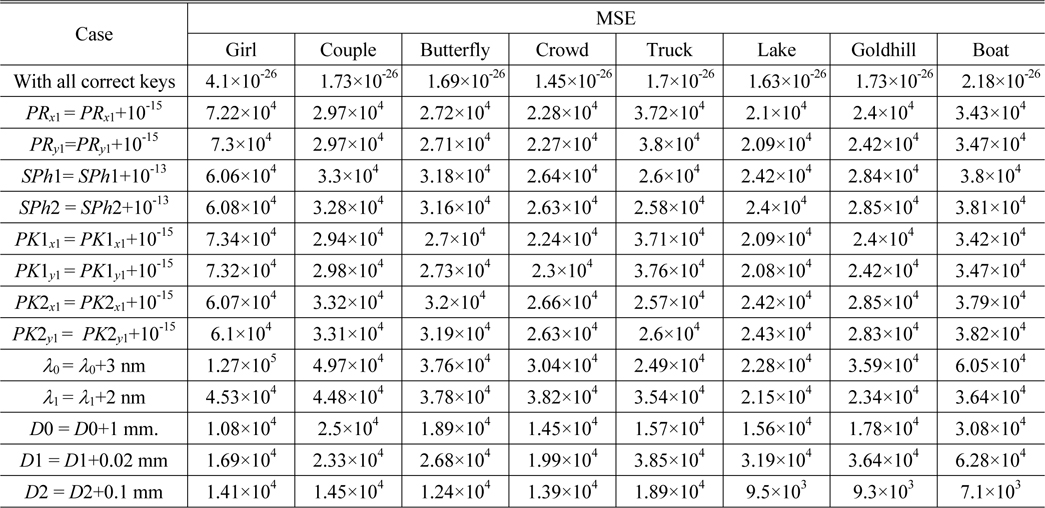
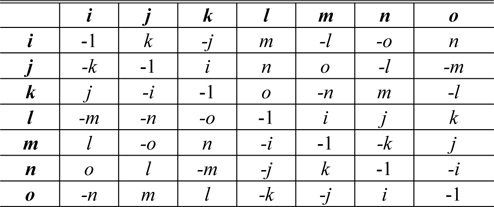
The addition and subtraction of octonions are performed by adding and subtracting corresponding terms [25]. However, the multiplication of octonions is neither commutative nor associative [24, 25]. The multiplication rules, which describe the result of multiplying the element in the pth (p= 1, 2, ⋯, 7) row by the element in the qth (q= 1, 2,⋯, 7) column, are given in Table 1 [25].
The conjugate and modulus of an octonion are respectively defined by [25]
When ζ0 = 0, ON is a pure octonion.
The Fresnel transform of a function f(x,y) is given by [26]
where FSTD[•] denotes the Fresnel transform with respect to D. In Eq. (4), D is the diffraction distance, λ is the wavelength, and (x,y) and (u,v) are the coordinates of the input and the transform planes respectively.
Since the FST of f(x,y) is a complex function, F(u,v) can also be expressed as follows
where Re(x) and Im(x) represent respectively the real and imaginary parts of the complex number x.
For simplicity, let P=π[2D2+(u-x)2+(v-y)2]/(λD). According to Euler’s formula exp(jx)=cosx+jsinx, Eq. (4) can be rewritten as
Comparing Eqs. (5) and (6), the real and imaginary parts of f(x,y) after FST are as follows
The inverse Fresnel transform (IFST) means an FST of a Fresnel diffraction pattern with the distance parameter – D [27].
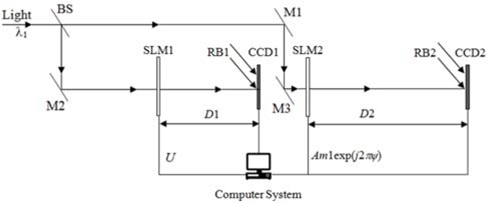
Based on the amplitude-truncated and phase-truncated strategy, an asymmetric cryptosystem in the Fresnel domain was reported in [15]. Figure 1 shows the schematic optical encryption setup for this asymmetric cryptography [15]. In Fig. 1, three planes are defined as the input plane, the transform plane, and the output plane. The corresponding coordinates of the three planes are denoted respectively by (x0,y0), (s,t) and (x1,y1). The distances between adjacent planes are D1 and D2. Two random phase masks RPM1 and RPM2 are located in the input plane and the transform plane, respectively.
In the asymmetric encryption method in the Fresnel domain, when the system is illuminated by a collimated plane wave of wavelength λ, the input image f(x0,y0) modulated by RPM1 is transformed by FST with respect to D1, and a complex distribution can be obtained. The real amplitude and phase maps of the complex distribution just before RPM2 can be extracted by employing the angular spectrum algorithm, to describe the free-space propagation process [15]. Then the achieved real amplitude multiplied by RPM2 is Fresnel transformed with respect to D2. Similarly, the real amplitude and phase maps of the Fresnel spectrum in the charge-coupled device (CCD) plane can be extracted. This last amplitude is the final ciphertext and the two phase maps are use as decryption keys. Since amplitude and phase maps can be displayed by a spatial light modulator (SLM), the asymmetric cryptosystem in the Fresnel domain can be implemented by an optical or digital approach [15].
Due to their excellent properties, such as sensitivity to initial conditions and control parameters, chaotic maps are employed to encrypt the image, which can strengthen the nonlinearity of the image [8]. Since 2D-SLMM offers a wider chaotic range and better ergodicity and hyperchaotic properties than existing chaotic maps [28], it has been chosen to design the scrambling method and generate the RPMs in this study. 2D-SLMM is defined as [28]
where 0 ≤ α ≤ 1 and 0 ≤ β ≤3 are control parameters. When β is close to 3, 2D-SLMM exhibits good chaotic performance [28].
Similar to Eq. (4), the right-side OFST with respect to D and λ is defined by Eq. (10), due to the noncommutative and nonassociative multiplication properties of octonions:
where foc(x,y) is a two-dimensional octonion function and μ is a pure unit octonion meeting the constraint that μ2 = -1 [29, 30]. OFST() denotes the OFST operation.
Corresponding to OFST, the inverse right-side OFST (IOFST) is defined as
Here, IOFST() is the IOFST operation. OFST and IOFST are transformation pairs of each other. They ensure that an octonion function foc(x,y) that is transformed into the OFST domain can be reconstructed completely by the inverse process, without losing any information.
The method that utilizes the existing FST algorithm to calculate the OFST of an octonion matrix is developed in this subsection. Using the FST algorithm, the OFST can be implemented efficiently.
Let P = π[2D2+(u-x)2+(v-y)2]/(λD). Using Euler’s Formula for Octonions, exp(μx)=cosx+μsinx [29], Eq. (10) can be rewritten as
Since foc(x,y) is an octonion function, it can be represented as
where f0(x,y), f1(x,y), f2(x,y), f3(x,y), f4(x,y), f5(x,y), f6(x,y), and f7(x,y) are real-value functions. For simplicity, let foc, f0, f1, f2, f3, f4, f5, f6, and f7 denote foc(x,y), f0(x,y), f1(x,y), f2(x,y), f3(x,y), f4(x,y), f5(x,y), f6(x,y), and f7(x,y) respectively in the following equations.
Considering the general unit pure octonion μ= γ1i + γ2j + γ3k + γ4l + γ5m + γ6n +γ7o (where γ1, γ2, γ3, γ4, γ5, γ6, and γ7 are real numbers), substituting foc and μ into (12), we have
Using Eq. (7), Eq. (15) can be obtained after calculating Eq. (14):
From Table 1, we have
Substituting Eqs. (2) and (16) into Eq. (15), we have
where
It can be seen from Eq. (18) that each coefficient in F0, F1, F2, F3, F4, F5, F6, and F7 contains the information of f0, f1, f2, f3, f4, f5, f6, and f7. Similarly, applying the right-side IOFST to Eq. (17), the reconstructed f’oc(x, y) can be obtained:
where
In Eq. (20), F0, F1, F2, F3, F4, F5, F6, and F7 denote F0(u,v), F1(u,v), F2(u,v), F3(u,v), F4(u,v), F5(u,v), F6(u,v) and F7(u,v) respectively.
As can be seen from formulas (14)-(20), the right-side OFST and IOFST of an octonion matrix can be calculated effectively using the traditional FST and IFST algorithms.
Singh et al. [22] and Liu et al. [31] stated that the security and the amount of RPM data of an encryption technique, in which the entire RPMs have to be sent to the receiver side to decrypt the original image, can be improved and reduced by employing a chaotic function to generate the chaotic random distributions that are use to construct the RPMs. He et al. [32] claimed that an optical security system can resist some potential attacks, such as chosen plaintext attack, by use of a scrambling technique. Since the chaotic sequences generated by 2D SLMM have the characteristics of a good random distribution, and are extremely sensitive to the initial value of the chaotic function, an SLMM-based RPM generation (SBRPMG) method and an SLMM-based scrambling (SBS) method are presented to generate the RPM and permute the positions of image pixels. Supposing the size of the input data image I(x,y) is M×N, the two methods are described as follows.
The procedure for generating the RPM can be described as follows:
1) Initialize X(1) and Y(1) randomly, then iteratively generate two one-dimensional (1D) chaotic sequences X = {X(p)} and Y = {Y(p)} using Eq. (9). Here the lengths of X and Y both are MN, and p = 1, 2, …, MN.
2) Compute the chaotic sequences X and Y using the following equation:
Here, fix(ρ) rounds each element of ρ to the nearest integer, down toward zero. All elements of X and Y belong to [0, 1].
3) Construct a new 1D sequence R with length MN using the following rule:
4) Convert the sequence R into a 2D matrix Φ with size M×N, which can be considered a random distribution.
5) With the random distribution Φ, the RPM, represented by exp[j2πΦ(x,y)] can be obtained.
The scrambling method is described as follows:
1) Initialize S(1) and T(1) randomly, then iteratively generate two 1D chaotic sequences S = {S(q)} and T = {T(q)} using Eq. (9). Here the lengths of S and T both are MN, and q = 1, 2, …, MN.
2) With S and T, produce a new 1D sequence W with length MN according to the following rule:
3) Using the quicksort algorithm [33], sort W in a certain (ascending or descending) order to obtain a new sequence W’ and its corresponding permutation indices IW. There are MN elements in IW. The relation between W and W’ is W’ = W(IW). For instance, the qth element in W’ corresponds to the IW(q)th element in W.
4) With IW, use the following loop procedure (described as pseudo-code) to permute the input data I, and the scrambled data EI can be obtained.
for (row=1; row≤M; row=row+1) { for (col=1; col≤N; col=col+1) { Pid = IW((row-1)×N+col); r = ceil(Pid/N); c = Pid - N×(r-1); EI(row, col) = I(r,c); } }
Here, ceil(ρ) rounds each element of ρ to the nearest integer greater than or equal to ρ. In the permutation process the values of the elements in the original image I are not changed, but their corresponding positions are varied.
The inverse image-scrambling (decryption) process is similar to the image-scrambling process. In decryption, first find the permutation indices IW as described in steps (1)-(3) with the same parameters. Then permute EI back to their original positions using the following loop procedure.
for (row=1; row≤M; row=row+1) { for (col=1; col≤N; col=col+1) { Pid = IW((row-1)×N+col); r = ceil(Pid/N); c = Pid - N×(r-1); DI(r,c) = EI(row, col); } }
In the above loop procedure, DI is the decrypted image.
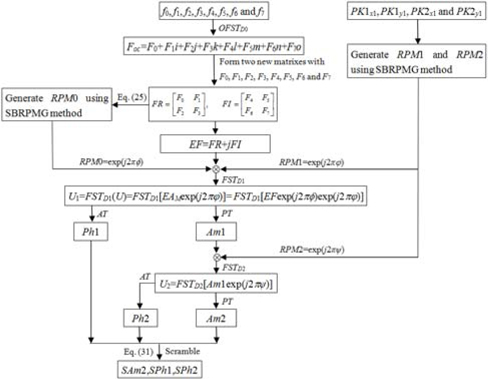
Since an octonion contains a real part and seven imaginary parts, eight images can be represented by an octonion, as shown in Eq. (13). Using this representation, eight images can be processed holistically in a vectorial manner using OFST. Therefore, based on the OFST and 2D-SLMM, an asymmetric multiple-image encryption scheme in the Fresnel domain is presented. In the proposed method, at most eight images can be encrypted simultaneously. Since amplitude and phase can be modulated simultaneously by an SLM [35], the proposed method can be implemented using an optical or digital approach. Figure 2 shows the optoelectronic setup of the proposed encryption process. In Fig. 2, BS is a beam splitter, M1, M2, and M3 are mirrors, and RB1 and RB2 are two reference beams that are split from the light source. SLM1, CCD1, and CCD2, which are computer-controlled, are located respectively in the input plane, the transform plane, and the output plane. Supposing f0, f1, f2, f3, f4, f5, f6, and f7 denote eight grayscale images of size M×N respectively, the steps of the encryption procedure are described as follows.
1) To treat the eight images in a holistic manner, f0, f1, f2, f3, f4, f5, f6, and f7 are represented by an octonion: foc = f0 + f1i + f2j + f3k + f4l + f5m + f6n + f7o.
2) With the distance D0 and the wavelength λ0, foc is transformed by OFST: Foc = OFSTD0(foc) = F0 + F1i + F2j + F3k + F4l + F5m + F6n + F7o. Here, F0, F1, F2, F3, F4, F5, F6, and F7 are computed using Eq. (18).
3) Using F0, F1, F2, F3, F4, F5, F6, and F7, construct two new matrixes of size 2M×2N using the following formula.
4) Let EF = FR+jFI. EF can be regarded as the complex amplitude that will be encrypted in the Fresnel domain. The size of EF is 2M×2N.
5) To enhance robustness against attacks such as the known public key attack, the complex amplitude EF is modulated by a phase mask RPM0, mathematically represented by the function EFM(x0,y0) = EF(x0,y0)exp [j2πΦ(x0,y0)]. Here, RPM0 = exp[j2πΦ(x0,y0)] is generated using the SBRPMG with initial parameters PRx1 and PRy1. That is, RPM0 = SBRPMG(PRx1, PRy1, 2M, 2N), where SBRPMG() is the SLMM-based RPM generation operation. The parameters PRx1 and PRy1 correspond to X(1) and Y(1) described in step 1 of subsection 4.1, and are obtained using the following formula:
where mean(x) returns the mean value of x. |x| returns the absolute value or the complex magnitude of x.
6) The complex amplitude EFM is then multiplied by a random phase mask RPM1=SBRPMG(PK1x1, PK1y1, 2M, 2N)=exp[j2πΦ(x0,y0)]. Here the initial parameters PK1x1 and PK1y1 are two random numbers in the range (0, 1). So the complex amplitude can be written as U(x0,y0)=EFM(x0,y0)exp[j2πΦ(x0,y0)].
7) Import U(x0,y0) into SLM1, which is located in the input plane and under computer control. When the system is perpendicularly illuminated by a plane wave of wavelength λ1, U(x0,y0) is then transformed by FST with respect to D1. The complex distribution U1(s,t) can be represented by
where FST() is the Fresnel transform operation. Then the amplitude Am1(s,t) and phase function Ph1(s,t) of the complex distribution can be extracted with the PT and AT operations
where PT() denotes tphase truncation, the operation of truncating the phase part while retaining the amplitude part [19], and AT() stands for amplitude truncation, the operation of truncating the amplitude part while retaining the phase function distributed on the interval [0,2π ] [8, 19].
8) Subsequently, the real amplitude Am1(p,s) multiplied by another random phase mask RPM2 =S BRPMG (PK2x1, PK2y1, 2M, 2N) = exp[j2πψ (s, t)]. is fed into SLM2, and then transformed to another complex distribution using FST with D2 and λ1. Here the initial parameters PK2x1 and PK2y1 are also two random numbers in the range (0, 1). The resultant distribution can be written as
The amplitude of the resultant distribution, which is the encrypted signal, and the corresponding phase function are obtained by the PT and AT operations as follows:
9) To enhance security, Am2, Ph1, and Ph2 are permuted by the proposed SBS method mentioned in subsection 4.2, as follows:
where SBS() is the SLMM-based scrambling operation. SAm2 is the final ciphertext of the proposed encryption scheme. The parameters SKs1 and SKt1 correspond to S(1) and T(1) in step 1 of subsection 4.2, and are obtained using the following formula:
where rdp(x,dn) is the operation that retains the dnth decimal place of x, dn being an integer. That is, x is accurate to the dnth decimal place.
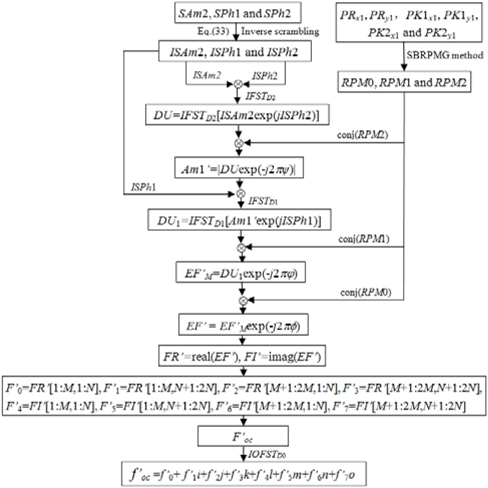
In the encryption process mentioned above, steps (1)-(6) and (9) will be performed digitally. As shown in Fig. 2, the complex function U obtained in step (6) is fed into the SLM1 and illuminated by a monochromatic light, then recorded by CCD1. The phase-truncated part Am1 of the Fresnel spectrum may be generated by CCD1 [11]. The corresponding amplitude-truncated part Ph1 may be generated by interferometry with the reference beam RB1, which is split from the light source [19]. Subsequently, the obtained real amplitude Am1 multiplied by RPM2 is imported into SLM2, and then Fresnel transformed. Similarly, the amplitude and phase of the resultant distribution can be measured by interferometry with reference beam RB2 and CCD2. RB2 is also split from the light source. The extracted amplitude and phase are stored in a computer. After scrambling the last amplitude, the final ciphertext can be obtained. The two obtained phase functions are reserved as decryption keys. Figure 3 is the flowchart of the encryption process. In Fig. 3, the symbol denotes multiplication.
In the proposed encryption method, the parameters D0, D1, D2, λ0, λ1, PK1x1, PK1y1, PK2x1, and PK2y1 are used as the encryption keys, while PRx1, PRy1, SPh1, and SPh2, which are derived in the encryption procedure and directly related to the plaintext images, are used as decryption keys. Additionally, the decryption keys are totally different from the encryption keys. The encrypted data can be decrypted correctly by using not only the encryption keys but also the decryption keys. With the aforementioned encryption and decryption keys, this cryptosystem enlarges the key space markedly. Since the initial values of the 2D SLMM function are used to generate the RPMs in decryption, there is no need to send the whole RPMs to the receiver for decryption, which drastically reduces the amount of key data. It is worth noting that the scrambling parameters SKs1 and SKt1 in step (9) do not need to be saved as secret keys, because they can be calculated from the private keys SPh1 and SPh2 during decryption.
In addition, eight grayscale images all of size M×N can be encrypted into one of size 2M×2N, which means the compression ratio of the proposed encryption method can be 1:2.
The steps of the decryption process are given as follows.
1) The ciphertext SAm2 and decryption keys SPh1 and SPh2 are permuted by the proposed inverse scrambling procedure as follows:
where ISBS() is the inverse SLMM-based scrambling operation. The parameters ISKs1 and ISKt1 are obtained using the following formula:
2) ISAm2 and exp(jISPh2) are multiplied and then transformed by IFST with respect to D2 and λ1:
where IFST() is the inverse Fresnel transform operation.
3) DU(s,t) is multiplied by the conjugate of RPM2, which is generated using the SBRPMG method with encryption keys PK2x1 and PK2y1, to obtain Am1’(s,t):
4) Am1’(s,t) and exp(jISPh1) are multiplied and then transformed by IFST with respect to D1 and λ1:
5) DU1(x0,y0) is multiplied by the conjugate of RPM1, which is generated using the SBRPMG method with encryption keys PK1x1 and PK1y1, to obtain EF’M(x0,y0):
6) EF’M(x0,y0) is multiplied by the conjugate of RPM0, which is produced using the SBRPMG method with decryption keys PRx1 and PRy1, to obtain EF’ (x0,y0):
7) Take the real part FR’ and imaginary part FI’ of EF’ (x0,y0):
where real(x) and imag(x) are the operations that return respectively the real and imaginary parts of the elements of x.
8) First, let F’0 = FR’[1:M, 1:N], F’1 = FR’[1:M, N+1:2N], F’2 = FR’[M+1:2M, 1:N], F’3 = FR’[M+1:2M,N+1:2N], F’4 = FI’[1:M, 1:N], F’5 = FI’[1:M, N+1:2N], F’6 = FI’[M+1:2M,1:N], and F’7 = FI’[M+1:2M,N+1:2N]. Thenlet F’oc = F’0+ F’1i+ F’2j+ F’3k+ F’4l+ F’5m+ F’6n+ F’7o.
9) Apply IOFST to F’oc to find f’oc:
Thus, f’0, f’1, f’2, f’3, f’4, f’5, f’6, and f’7 are the decrypted images.
As can be seen from Eqs. (31) and Eq. (33), the mean values of Ph1, Ph2, SPh1, and SPh2, denoted by mPh1, mPh2, mSPh1, and mSPh2 respectively, are used to calculate SKs1, SKt1, ISKs1, and ISKt1, which are the initial parameters of the scrambling and inverse-scrambling methods respectively. In theory, mPh1 and mPh2 are identical to mSPh1 and mSPh2, since the values of the elements in Ph1 and Ph2 are not changed, though their corresponding positions are varied in the permutation process. However, because of the limited number of significant digits (e.g. the number of significant digits for double-floating-point numbers in C programming languages is 15) [34], the different computation order between the elements of Ph1 and those of SPh1 in calculating the mean, the different computation order between the elements of Ph2 and those of SPh2 in calculating the mean, and rounding, mPh1 and mPh2 are slightly different from mSPh1 and mSPh2 respectively. Hence the rdp(x,dn) operation is used to eliminate the slight differences between mPh1 and mSPh1, and between mPh2 and mSPh2 in Eqs. (31) and Eq. (33). In the experiments, dn is 12.
Figure 4 depicts the decryption process. In Fig. 4, conj (RPM2), conj(RPM1), and conj(RPM0) are respectively the conjugates of RPM2, RPM1, and RPM0.
To verify the feasibility of the proposed encryption technique, numerical simulations are performed on the eight grayscale images “Girl”, “Couple”, “Butterfly”, “Crowd”, “Truck”, “Lake”, “Goldhill” and “Boat”, all of size 256×256, shown in Fig. 5. The tests are carried out on a notebook computer with Intel(R) Core(TM) i7-4700HQ CPU @ 2.40 GHz and 8 GB of DDRL3 RAM, and with MATLAB R2013a. In the experiments, the system parameters are μ = (i+j+k+l+m+n+o)/71/2 [29], α = 0.998, β = 3, D0 = 50 mm, D1 = 20 mm, D2 = 30 mm, λ0 = 537.8 nm, λ1 = 632.8 nm, PK1x1 = 0.41, PK1y1 = 0.52, PK2x1 = 0.36, PK2y1 = 0.75, and dn = 12, and a pixel size of 6.72 μm is used in the input plane. To evaluate the quality of the decrypted image, the mean square error (MSE) between the original plaintext image and the decrypted image is calculated as follows:
where f(m,n) denotes the original plaintext image and f’(m,n) is the corresponding decrypted one.
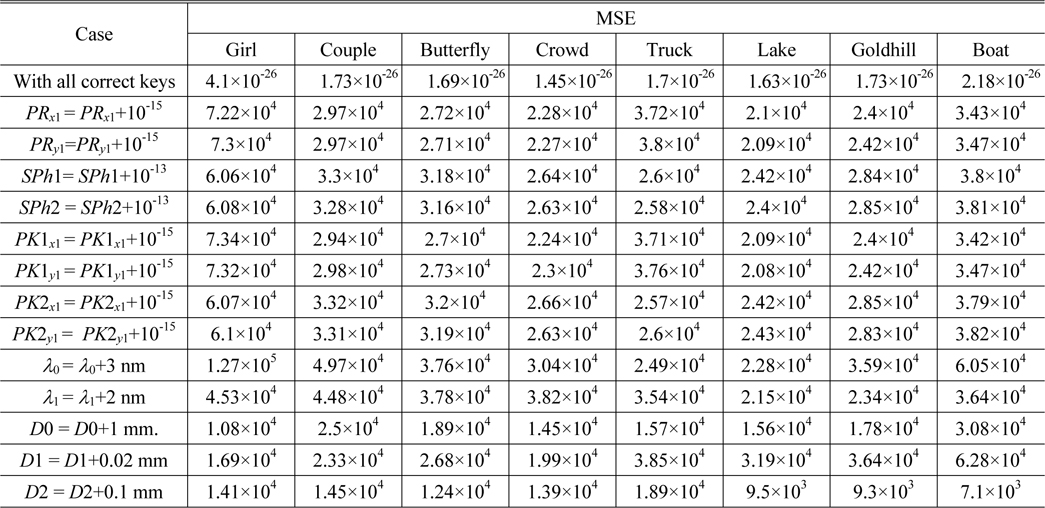
Using the proposed encryption scheme, the eight plaintext images are encrypted, and the ciphertext shown in Fig. 6(a) is obtained. To investigate the performance of the proposed scheme, the ciphertext is decrypted using both correct and incorrect keys. The MSEs between original and decrypted images are listed in Table 2. Figs. 6(b)-(i) display the eight images retrieved with the correct keys respectively. They are perfect, without any noise or distortion. As shown in Table 1, all the corresponding MSEs are approximately zero.
As a multiple-image encryption scheme based on an asymmetric technique, the decryption keys play an important role. To evaluate the influence of the decryption keys, cases in which PRx1, PRy1, SPh1, and SPh2 have been slightly changed are explored. Figures 7 and 8 show the images decrypted with the wrong keys PRx1 = PRx1+10-15 and PRy1 = PRy1+10-15. The private keys SPh1 and SPh2, in which every element is changed by 10-13 and also represented as SPh1 = SPh1+10-13 and SPh2 = SPh2+10-13, have been use to decode the ciphertext; Figs. 9 and 10 are the corresponding decoded images. From Table 2, all the MSE values of the decrypted images in Figs. 7-10 are greater than 2×104. Experiments indicate that the decrypted results are noiselike images and cannot afford any valid information when the absolute values of the deviations of PRx1 and PRy1 are up to 10-15, and those of SPh1 and SPh2 are up to 512×512×10-13. Therefore, the decryption keys are highly sensitive to the proposed method.
Now we investigate the sensitivity of retrieved images to a small change in the parameters of the 2D SLMM-based RPM generation technique. Figs. 11-14 show the images decrypted with the wrong keys PK1x1 = PK1x1+10-15, PK1y1 = PK1y1+10-15, PK2x1 = PK2x1+10-15, and PK2y1 = PK2y1+10-15 respectively. The corresponding MSEs are listed in Table 2. As illustrated in Figs. 11-14, we cannot obtain any information visually from the decrypted images when the absolute values of the deviations of the encryption keys PK1x1, PK1y1, PK2x1, and PK2y1 are up to 10-15. It can be seen from Table 2 that all of the MSEs of the decoded images in Figs. 11-14 are greater than 2×104. Thus it can be concluded that the decrypted images cannot be recognized if the keys of the RPM generation system are changed even slightly. Experimental results convincingly demonstrate that illegal users cannot access the security system without the correct RPMs.
The performance of security parameters D0, D1, D2, λ0, and λ1 is further examined during decryption. Figure 15 displays the decrypted images, which are seriously degraded and almost unrecognizable, when an error of 3 nm exists for the wavelength λ0. Figure 16 shows the decrypted images that cannot be recognized when errors of 2 nm exist for the wavelength λ1. Figure 17 exhibits the retrieved images, which are almost unrecognizable, when an error of 1 mm exists for the distance D0. The behavior of the proposed security system is also sensitive to the distances D1 and D2: Figs. 18 and 19 show the recovered images which are decoded with deviations of 0.02 mm and 0.1 mm in D1 and D2 respectively. As can be seen from Figs. 18-19, the retrieval images cannot be recognized correctly when D1 or D2 departs even slightly from the correct value. Almost all of the MSE values of the decrypted images shown in Figs. 15-19 are greater than 104. Therefore, from the simulation results we can see that the five encryption keys above can increase the security of the proposed system.
Please note that in the aforementioned experiments, the other keys remain correct while a key is changed (except for the experiment carried out with all correct keys).
Next, we evaluate the key space of the proposed asymmetric encryption method. In term of the description of the proposed scheme, we know that the key space of the cryptosystem consists of the encryption keys D0, D1, D2, λ0, λ1, PK1x1, PK1y1, PK2x1, and PK2y1, and the decryption keys PRx1, PRy1, SPh1, and SPh2. The key spaces of the security keys D0, D1, D2, λ0, λ1, PK1x1, PK1y1, PK2x1, and PK2y1, which are denoted by Z1, Z2, Z3, Z4, Z5, Z6, Z7, Z8, and Z9 respectively, are analyzed as follows: Since different wavelengths and diffraction distances can be used to encode and decode the plaintexts, we suppose that the distances are in the range of 10 to 110 mm, and the wavelengths from 400 to 750 nm, in the experiments. Considering that the sensitivities to D0, D1, D2, λ0, and λ1 are 1 mm, 0.02 mm, 0.1 mm, 3 nm, and 2 nm respectively, the three distances can be varied with steps of 1 mm, 0.01 mm and 0.1 mm in the range from 10 to 110 mm, and the two wavelengths can be varied with steps of 1 nm in the range from 400 to 750 nm; so Z1×Z2×Z3×Z4×Z5 = (100/1) ×(100/0.01) ×(100/0.1) ×(350/1) ×(350/1) ≈ 1.2×1014. From Figs. 11-14, the parameters PK1x1, PK1y1, PK2x1, and PK2y1 maintain 15, 15, 15, and 15 digits after the decimal point respectively; thus Z6×Z7×Z8 ×Z9 = 1060. For the decryption keys, the key spaces of PRx1, PRy1, SPh1 and SPh2, denoted by Z10, Z11, Z12, and Z13 respectively, should also be analyzed. From Figs. 7 and 8, the parameters PRx1 and PRy1 maintain 15 and 15 digits after the decimal point respectively; thus Z10×Z11 = 1030. Considering that the sensitivities to SPh1 and SPh2 both are 512×512×10-13 ≈ 2.6×10-8, these two decryption keys can be varied with steps of 10-8 in the range [0, 512×512×2π], which results in Z12×Z13=(512×512×2π/10-8)2 ≈ 2.7×1028. Hence, the entire key space of the cryptosystem is Z1×Z2×Z3×Z4×Z5×Z6×Z7×Z8×Z9×Z10×Z11×Z12×Z13 = 1.2×1014 ×1060×1030×2.7×1028 ≈ 3×10132 ≈ 2440. As reported in [36], to obtain a high level of security, key space should at least be larger than 2100. It is obvious that the key space of the proposed cryptosystem is far greater than 2100, and huge enough to resist a brute-force attack.
Information loss or noise contamination may occur during data transmission. Now, the robustness of this method against occlusion attack, which is viewed as data loss, is tested. Figure 20(a) shows the ciphertext occluded by 25%. The retrieved images acquired by employing all correct keys are illustrated in Figs. 20 (b)-(i). All of the decrypted images can be distinguished, and their corresponding MSEs are 2.95×103, 1.98×103, 1.93×103, 1.76×103, 1.74×103, 1.7×103, 1.82×103, and 2.13×103. It is well known that Gaussian noise [37] and salt-and-pepper noise [37] appear frequently during transmission. The robustness of the cryptosystem against noise attacks is further probed. Figure 21(a) is the ciphertext polluted by Gaussian noise with mean value 0 and standard deviation 25. Figures 21(b)-(i) are the recovered images, and their corresponding MSEs are 3.77×104, 1.38×104, 1.27×104, 8.19×103, 7.65×103, 6.35×103, 104, and 1.81×104. Figure 22(a) shows the ciphertext damaged by salt-and-pepper noise with density 0.05. Figures 22(b)-(i) depict the retrieved images with corresponding MSEs of 3.74×104, 1.36×104, 1.26×104, 8.12×103, 7.59×103, 6.27×103, 9.92×103, and 1.78×104. Although all the results displayed in Figs. 21(b)-(i) and 22(b)-(i) are interfered with seriously by noise, and the corresponding MSEs are large, the decrypted images can still be recognized among the noise.
Four potential attacks, including cipher only attack, known plaintext attack, chosen plaintext attack and chosen ciphertext attack [8], are usually utilized to attack an optical security system to retrieve ciphered images. If a cryptosystem can resist chosen plaintext attack, the most powerful one, then it can resist other attacks [38]. He et al. stated that scrambling techniques can prevent the attacker from accessing the ciphertext acquired from the cryptosystem in such attacks [32]. For the proposed multiple-image encryption scheme, assuming an attacker knows all the encryption keys, including D0, D1, D2, λ0, λ1, PK1x1, PK1y1, PK2x1, and PK2y1, he can encrypt eight false plaintext images and deduce the decryption keys PRx1, PRy1, SPh1, and SPh2 by utilizing the chosen plaintext attack depicted in [10]. Subsequently, the attacker can crack the original ciphertext with the achieved decryption keys and the encryption keys. In the experiment, the private keys PRx1, PRy1, SPh1, and SPh2 are generated by choosing the eight images shown in Fig. 23 as the false plaintext images, and then employed to decrypt the ciphertext shown in Fig. 6(a). Figure 24 shows the decoded images, from which no valuable information can be acquired, though the content of the eight false images can be seen faintly. The corresponding MSEs are 2.26×104, 1.31×104, 1.42×104, 1.35×104, 1.2×104, 1.05×104, 9.8×103, and 1.68×104. Due to the linearity of the system, the DRPE-based encryption technique is vulnerable to chosen plaintext attacks [8, 9]. From the experimental results, the nonlinearity of the proposed cryptosystem is strengthened. As stated in [38], the proposed encryption approach can also resist the other aforementioned attacks.
Ding et al. reported a known public key attack on an asymmetric optical image cryptosystem [13], in which an illegal user can deduce the decryption keys by encrypting a false real-value plaintext image whose amplitudes are 1, if he knows all public (encryption) keys; then he can use the obtained decryption keys to decrypt the original ciphertext. To test the robustness of this scheme against known public key attack, eight real-value images whose amplitudes are 1 are used as false plaintext images to obtain the decryption keys. Subsequently, the original ciphertext shown in Fig. 6(a) is decrypted using the obtained decryption keys. Figure 25 displays the images retrieved using the decryption keys obtained from the known public key attack. As illustrated in Fig. 25, no information can be gained from the noiselike decoded images. The corresponding MSEs are 1.66×104, 1.65×104, 1.66×104, 1.66×104, 1.65×104, 1.65×104, 1.66×104, and 1.66×104. Therefore, the proposed asymmetric cryptosystem can resist the known public key attack effectively.
The computational complexity of the proposed encryption method is estimated, since the encrypted results were obtained by computer from numerical simulation. The estimation depends on three main factors: First, to process eight images holistically in a vectorial manner, the OFST is computed one time. In light of the calculation method developed in subsection 3.2, the OFST can be implemented by computing the FST eight times. For an image of size M×N, the cost to calculate the FST is O(2MN + MN log2 MN) [39]. Hence, if the computations of additions are omitted, the complexity of the OFST calculation is O(8MN log2 MN + 16MN). The second factor is the complexity of the virtual optical encryption process, in which three RPMs are generated by the SBRPMG method first, then the input information is modulated three times using the RPMs, and transformed two times by employing the FST. In addition, the phase truncation and amplitude truncation are performed two times respectively. For a matrix of size M×N, the complexities of RPM generation, modulation operation, FST operation, PT operation, and AT operation are O(6MN), O(MN), O(2MN) +O(MN log2 MN) , O(MN) and O(MN) respectively. Since the size of the complex amplitude is 2M×2N, the computational cost of this procedure is O(3(6(4MN)) + 3(4MN) + 2(2(4MN) + 4MN log2 4MN) + 2(4MN) + 2(4MN)) = O(8MN log2 MN + 132MN). The last factor represents the three permutations due to the proposed SLMM-based scrambling method. In each permutation, the 2D SLMM operation, 1D sequence construction, the quicksort algorithm, and the loop procedure for scrambling the elements of the matrix are performed one time each. For a matrix of size M×N, the corresponding complexities of these four operations are O(2MN), O(MN), O(MN log2 MN), and O(4MN). Because the size of each of the three matrices to be scrambled is 2M×2N, the complexity of the permutation procedure is O(3(2(4MN)) + 4MN + 4MN log2 4MN + 4(4MN) = O(12MN log2 MN + 108MN). Thus the total computational complexity of the proposed cryptosystem is O(28MN log2 MN + 256MN).
In this paper, first a new definition of octonion Fresnel transform and its implementation are presented. Then, a novel asymmetric multiple-image encryption method based on nonlinear amplitude truncation and phase truncation in the Fresnel domain is proposed, in which the OFST combined with the designed SLMM-based pixel scrambling technique is used to encrypt multiple images. By utilizing OFST, as many as eight images can be processed holistically in a vectorial manner, the result being that the complexity of the cryptosystem can be reduced effectively, without losing security. The original images fail to be retrieved unless all of the correct keys, ifor both encryption and decryption, are provided. Simulation results and analyses verify that the proposed cryptosystem features extreme sensitivity to the precise values of the keys, a vast key space to resist brute-force attack, and a high robustness against occlusion, Gaussian noise, salt-and-pepper noise, chosen plaintext attack, and known public key attack. In addition, compared to traditional encryption methods in which entire RPMs must be sent to the receiver side for decryption, the proposed scheme has the advantage that only the seed values of the SLMM function are needed to generate the RPMs for decrypting the ciphertext. Thus there is no need to send the whole RPMs to the receiver side for decryption.




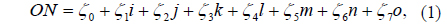
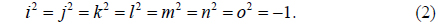
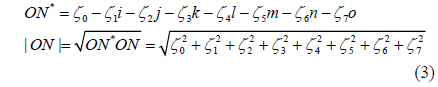
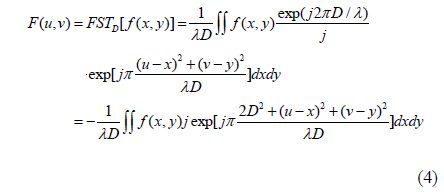
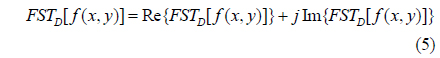
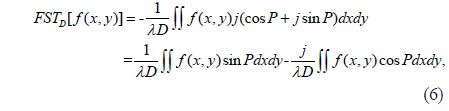

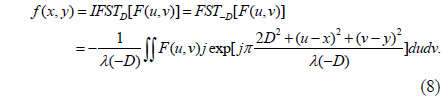
![A schematic optical experimental arrangement for asymmetric cryptography in the Fresnel domain [15].](http://oak.go.kr/repository/journal/20657/E1OSAB_2016_v20n3_341_f001.jpg)