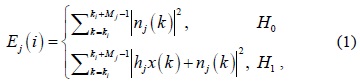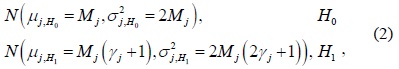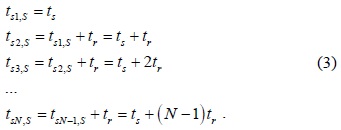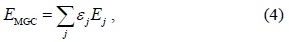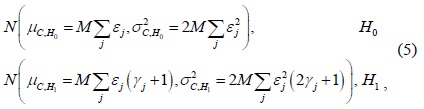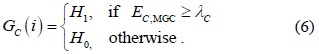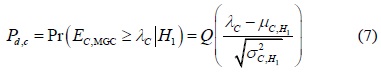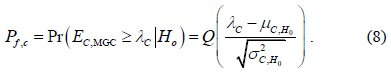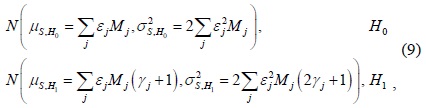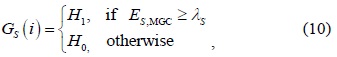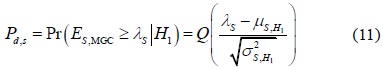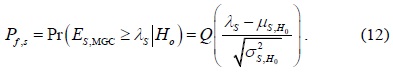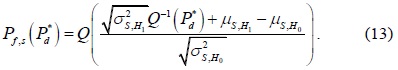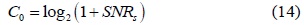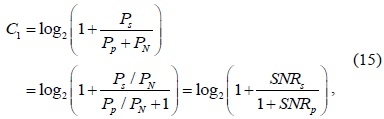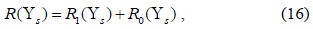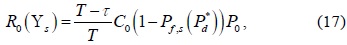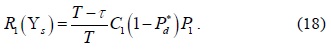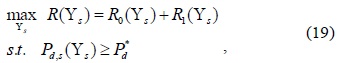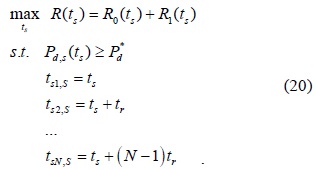In recent years, greater bandwidth and higher bit rates have been required to meet the increased usage demands caused by the explosion of wireless communication technology. According to the Federal Communications Commission spectrum policy task force report [1], the actual utilization of a licensed spectrum varies from 15% to 80%. Therefore, cognitive radio (CR) technology [2] has been proposed to solve the problem of the ineffective utilization of spectrum bands. The scarcity of spectrum bands can be relieved by allowing some cognitive users (CUs) to opportunistically access the spectrum assigned to the primary user (PU) whenever the channel is free. However, CUs must vacate their frequency when the presence of a PU is detected. Therefore, reliable detection of the PU signal is an essential requirement of CR networks.

To ascertain the presence of a PU, CUs can use one of the several common detection methods, such as the matched filter, feature, and energy detection methods [2,3]. Energy detection is an optimal detection method if the CUs have limited information about the PU signal (e.g., if only the local noise power is known) [3]. Improved spectrum usage detection can be obtained by allowing some CUs to perform cooperative spectrum sensing (CSS) [4-6].

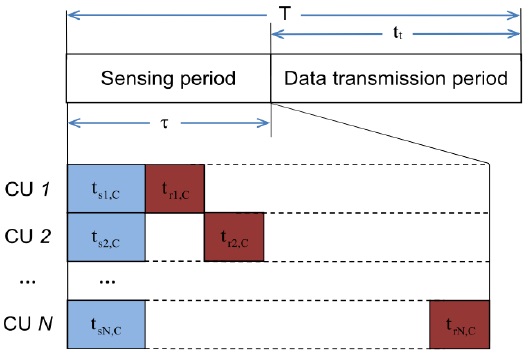
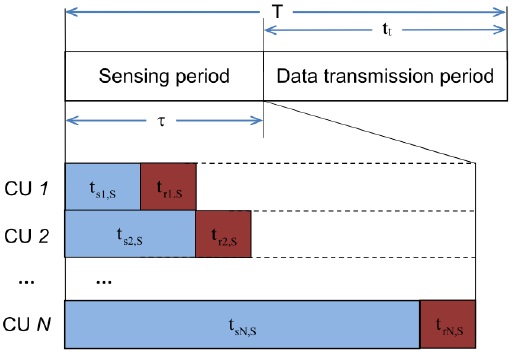
In conventional CSS, the time frame is divided into two main parts, namely the sensing and the data transmission parts. In the sensing part, all CUs take the same amount of time to perform spectrum sensing, and then, because of the limitations of the control channel, the CUs report their sensing results to the fusion center (FC) one by one, while the other CUs remain silent. On the other hand, the superposition cooperative spectrum sensing (SPCSS) proposed in [7], which allows CUs to extend their sensing times to the reporting slots of the others, can improve the sensing performance of CSS without requiring any more time for the sensing part. The trade-off between the sensing time and the throughput was studied in [8] for conventional CSS, in which the optimal sensing time for all CUs that maximize the throughput of the CR system was determined. Since the optimal sensing time obtained by [8] is the same for all CUs, it may not apply to SPCSS, in which each CU is assigned a different sensing time according to the reporting order of the CUs. Subsequently, the problem of determining the optimal sensing time for SPCSS is still open and needs more research on throughput maximization.

In this paper, we propose an algorithm to determine the optimal sensing time for SPCSS, with which the system can achieve the maximum throughput. In the proposed algorithm, we consider the reliability of the CUs (i.e., the signal-to-noise ratio (SNR) of the sensing channel) to decide the reporting order of the CUs. According to this order, the proposed algorithm determines the optimal sensing time for all the CUs in the network. Thus, we expect the proposed scheme to offer a higher throughput for CR networks than the conventional CSS scheme [8].

The rest of this paper is organized as follows: Section II describes the system model of the proposed scheme. Section III gives a detailed explanation of the proposed algorithm to find the optimal sensing time for maximizing the throughput of the CR system. Section IV introduces the simulation models and the simulation results of the proposed scheme. Finally, Section V concludes this paper.

In this study, we consider a network consisting of N CUs. Further, there is one PU occupying the observed band with a specific probability. The high accuracy of transmission from the CUs to the FC can be mostly guaranteed by using some error control methods. For example, an error detection and correction method can be used in which the error of the received data at the FC can be detected and corrected by using channel coding. An error detection and retransmission method in which the FC can ask the CUs to retransmit their sensing data when it receives the error data from the CUs can also be used. Therefore, in this study, we assume that the CUs can transmit their sensing data to the FC through an ideal reporting channel.

Each CU utilizes an energy detector for spectrum sensing. Then, at the i^th sensing interval, the received signal energy E_j(i) of the j^thCU is calculated as follows:

where H₀ and H₁ correspond to the hypotheses of the absence and the presence of the PU signal, respectively; x(k) represents the signal transmitted from the PU; h_j denotes the amplitude gain of the channel; n(k) indicates the additive white Gaussian noise; M_j = t_sjf_s represents the number of samples over a sensing interval; t_sj refers to the sensing time; f_s stands for the sensing bandwidth; and k_i denotes the time slot at which the i^th sensing interval begins.

When M_j is relatively large (e.g., M_j > 200), E_j can be well approximated as a Gaussian random variable for both hypotheses as follows [9]:

where N(‧) denotes the Gaussian distribution, μ_j,H0 and μ_j,H1 represent the mean of E_j for the H₀ and H₁ hypotheses, respectively; indicate the variance of E_j for the H₀ and H₁ hypotheses, respectively; and γ_j stands for the SNR of the sensing channel between the j^th CU and the PU. In general, the exact value of the SNR is not available for both the CUs and the FC. However, there are many studies on the estimation of the SNR, such as [10-12]. For CSS, the CUs and the FC can utilize one of these SNR estimation algorithms to estimate the SNR. Further, the main purpose of this study is to determine the optimal sensing time for SPCSS. Therefore, in this study, we assume that the SNR information is available in the FC.

The sensing result (i.e. received signal power) that the CUs sense from the PU’s signal will be reported to the FC. In conventional CSS, when a CU sends the sensing results to the FC, the other CUs remain silent and wait until their reporting time. In this case, all the CUs have the same sensing time, as shown in Fig. 1, such that t_s1,C=t_s2,C=…=t_sN,_C=t_s . On the other hand, SPCSS extends the sensing time of the CUs to the reporting time of the other CUs, as shown in Fig. 2. This implies that the CU that is the last CU reporting the sensing information to the FC will have the longest sensing time t_sN,_S , and the CU that reports first to the FC will have the shortest sensing time t_s1,S=t_s . Here, we assume that all CUs have the same reporting duration t_r1,S=t_r2,S=…=t_rN,_S=t_r . Then, the sensing time of all CUs in the case of the SPCSS can be expressed as follows:

At the FC, a maximum gain combination (MGC) rule is used for combining all the sensing results from the CUs as follows:

where ε_j denotes the weight of the j^th CU and is given as

Without any loss of generality, we assume that E_j and ε_j are independent for different CUs. Therefore, E_MGC can be approximated by a Gaussian distribution for both hypotheses of the PU signal.

In the conventional CSS, all CUs have the same number of sensing samples (i.e., the same sensing time) such that M=M₁=M₂=…=M_N . Subsequently, the distribution of the accumulated signal power at the FC, E_C,MGC , is expressed as follows:

where N denotes the normal distribution, and μ_C,H0 and μ_C,H1 represent the mean of E_C,MGC for the H₀ and H₁ hypotheses, respectively. denote the variance of E_C,MGC for the H₀ and H₁ hypotheses, respectively.

According to the value of E_C,MGC , the global decision G_C(i) will be determined as follows:

Here, λ_C denotes the threshold for the global decision of the conventional CSS.

The sensing performance of the conventional CSS can be evaluated by the probability of detection and the probability of false alarm as follows, respectively:

and

For the case of SPCSS, the CU that first reports its sensing information to the FC has the shortest sensing time, which is equal to the sensing time of conventional CSS. Other CUs will continue with spectrum sensing until their reporting rounds are reached. Therefore, different CUs will have a different number of sensing samples. Subsequently, the distribution of the accumulated signal power at the FC, E_S,MGC, is expressed as follows:

where M_j=f_s(t_s+(j-1)t_r) denotes the number of sensing samples of the j^th CU, f_s represents the sensing sample rate, and μ_S,H0 and μ_S,H1 indicate the mean of E_C,MGC for the H₀ and H₁ hypotheses, respectively. denote the variance of E_C,MGC for the H₀ and H₁ hypotheses, respectively.

As in conventional CSS, in SPCSS, the global decision is made as follows:

where λ_s denotes the threshold for the global decision of the SPCSS.

The sensing performance of the SPCSS can be evaluated by using the probability of detection and the probability of false alarm as follows, respectively:

and

Depending on the required value of the probability of detection P_d*, the probability of false alarm can be calculated as follows:

Suppose that τ denotes the time for the CUs performing spectrum sensing and reporting the sensing information to the FC. Then, we have τ=t_s+Nt_r . Therefore, the time that can be used for data transmission is t_t=T-τ , where T denotes the total frame time.

Let us consider C₀ to be the throughput of the CR network when it operates in the absence of the PU, and C₁ to be the throughput when it operates in the presence of the PU. Then, C₀ and C₁ can be calculated as follows:

and

where P_s denotes the received power of the CU, P_N represents the noise power, P_p indicates the interference power of the PU measured at the CU, SNR_s=P_s / P_N stands for the SNR of the CU–CU communication channel when the PU signal is absent, and SNR_P=P_p / P_N denotes the SNR received in the CU when the PU signal is present.

Let us define P₀ as the probability that the PU is idle and P₁ as the probability that the PU is active. Then, P₀+P₁=1 and the average throughput of the CR system can be expressed as follows:

where

Further, Y_s={T_s1,S, T_s2,S,…, T_sN,S} denotes the sensing times of all the CUs in the network.

Next, the problem of determining the optimal sensing time can be formulated as follows:

where denotes the required probability of detection of the CR network.

Further, the reporting time t_r is fixed for all the CUs (they report the same type of data to the same destination). Therefore, Y_s depends on t_s and the sensing order of each CU. In this study, we determine the sensing order of each CU according to its SNR in the sensing channel. That is, the CU with a higher SNR will be given a longer sensing time. Let us now arrange the CUs following an increase in the SNR; this implies that CU 1 has the lowest SNR and is the first in the sensing order with the lowest sensing time T_s1,S=t_s and that CU N has the highest SNR and is the last in the sensing order with the longest sensing time T_sN,S=t_s+(N-1)t_r . Subsequently, the problem in Eq. (19) can be rewritten as follows:

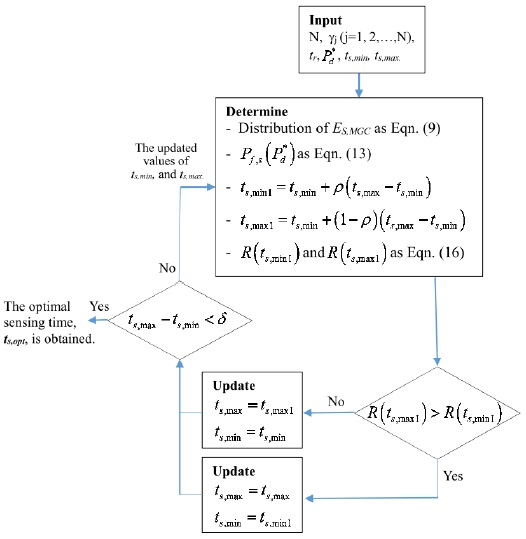
The problem in Eq. (20) can be solved to find the optimal sensing time t_s,opt and the maximum throughput of the system R(t_s,opt) by using a numerical method such as the Golden section search or a Fibonacci search method [13]. In this study, the Golden search method [13] is used for finding the optimal value of the sensing time. Initially, the range of the sensing time is experimentally determined to be t_s ϵ [t_s,min,t_s,max] .

On the basis of this range, we apply the Golden search method to find t_s,opt according to the flow chart shown in Fig. 3, where ρ=0.382 is a constant defined by the Golden search method [13].

In this section, we will present the simulation results to demonstrate the performance of the proposed scheme. We consider a CR network containing 10 CUs and 1 PU with the absence probability of P₀=0.8 . The required probability of detection is set as =0.95 . The reporting time is set as t_r = 0.001 s, which is similar to the IEEE 802.11 standard. Each CU independently senses the presence of the PU. For reference, the simulation results of the proposed scheme are compared with the results of [8].

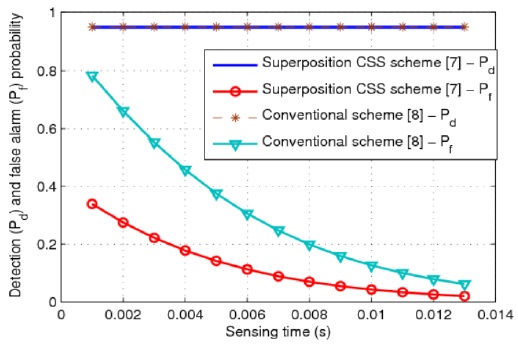
Fig. 4 shows the sensing performance at the FC of the CR network in terms of the probability of detection and the probability of false alarm P_f(t_s) when the SNR of the sensing channel of all the CUs is the same as γ_j = 17 dB. This shows that the SPCSS can improve the sensing performance (i.e., decrease the probability of false alarm) while maintaining the same probability of detection. Therefore, the SPCSS can increase the opportunity to utilize a free frequency band of the PU.

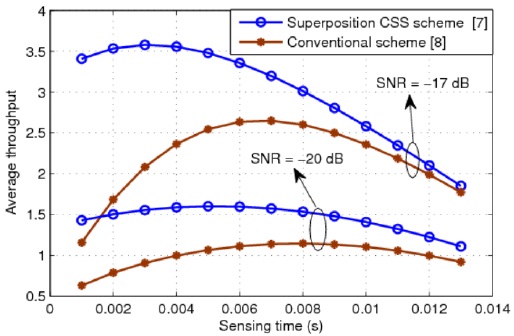
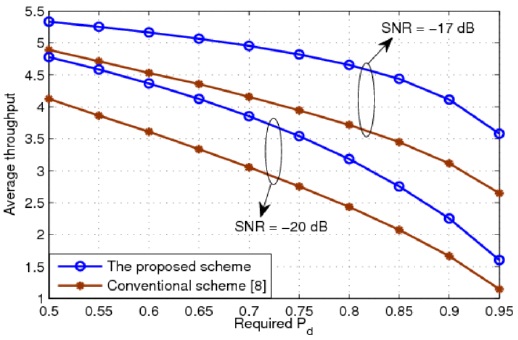
Fig. 5 presents the average throughput of the CR system for different values of the sensing time. It can be seen that SPCSS provides a considerable higher throughput than the conventional CSS. Further, at the same SNR in the sensing channel, the SPCSS needs a smaller sensing time to achieve the maximum average throughput than the conventional CSS. The average throughput of the CR system for different values of the required probability of detection is shown in Fig. 6. This figure proves that the proposed scheme can improve the throughput of the CR system. In other words, when the SNR of the sensing channel is –17 dB or –20 dB, the proposed scheme provides a throughput that is 30% or 40% higher than that of the conventional scheme, respectively.

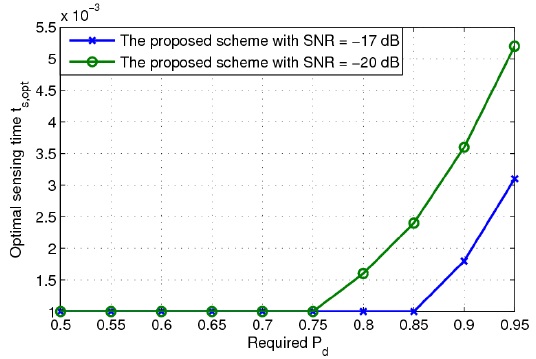
Fig. 7 shows the optimal sensing time t_s,opt for the achieved throughput shown in Fig. 6 for different values of the required probability of detection It can be seen that t_s,opt is dependent on the value of and that higher may require higher t_s,opt.

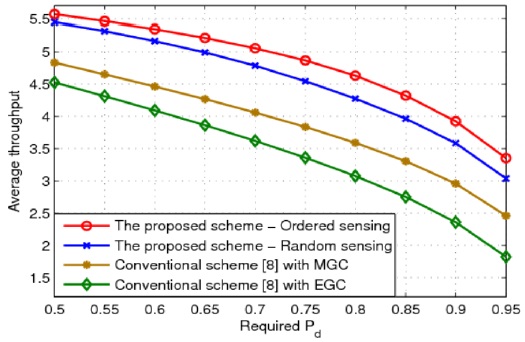
Fig. 8 shows the average throughput of the CR system for different values of the required probability of detection P_d when the network includes six CUs and each of them has a different SNR value; the SNR values of these six CUs are –24, –22, –20, –18, –16, and –13 dB, respectively. The performance values of four schemes, namely the proposed scheme that assigns a longer sensing time to a CU with a higher SNR (called the proposed scheme with ordered sensing), the proposed scheme that utilizes a random sensing order (called the proposed scheme with random sensing), conventional scheme proposed in [8] with MGC, and conventional scheme proposed in [8] with equal gain combination (EGC), are provided for reference. It can be seen that the proposed scheme with ordered sensing can achieve a better sensing performance than the proposed scheme with a random sensing order. Further, the proposed scheme always outperforms the conventional scheme. The conventional scheme with MGC has a better performance than the conventional scheme with EGC.

In this paper, we proposed an algorithm to find the optimal sensing time of all the CUs for SPCSS. In the proposed algorithm, ordered sensing was considered for assigning a longer sensing time to the CUs with higher SNR values and a shorter sensing time to the CUs with lower SNR values. The simulation results showed that the proposed scheme could significantly improve the throughput of the CR system, in comparison with the conventional scheme [8]. Moreover, we observed that the proposed scheme with ordered sensing achieved a better performance than the proposed scheme with a random sensing order. However, further research is required to analytically prove this conclusion. This will be our future work on this research topic.