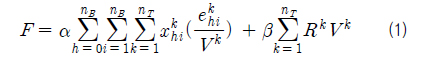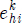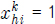선박 생산 과정은 강판 절단, 성형, 소 조립, 중 조립, 대 조립 등의 순차적인 단계를 거쳐 제작된 선박 건조 기본 단위인 블록이 선행 의장, 도장, PE를 거쳐 도크에서 탑재될 때까지 이동과 적치의 반복이다. 이 과정 중에 생산 공정 및 적치에 필요한 운반과정을 담당하는 것이 트랜스포터(transporter)이다. 공정 간혹은 지번 간 블록 이동이 비효율적으로 계획된다면 전체적인 물류비용이 증가하고, 증가한 물류비용은 전반적인 생산비용을 증가시킨다. 또한, 적치장의 운용효율이 떨어지고, 효율이 떨어진 만큼 물류 흐름이 원활히 이루어지지 않아 전체적인 생산 공정의 지연을 초래하여 막대한 손실을 일으킬 수 있으므로 트랜스포터의 물류 운영 계획은 대단히 중요하다. 이에 관한 기존 연구를 정리해 보면 다음과 같다.
Koo, et al. (2004)은 화물 컨테이너 운반시스템에서 최소의 차량으로 일정한 시간 내의 주어진 컨테이너를 운반하는 차량 경로계획을 설정하는 절차를 제시하였다. 제시된 절차는 우선 공차 이동 시간을 최소로 하는 최적화 모형을 이용하여 차량의 소요 대수 하한 값을 결정하고, Tabu Search 기반의 차량 경로 계획을 수립하였다.
Joo, et al. (2005)은 트랜스포터의 종류별 블록 운송 일정 계획을 세우기 위해 비슷한 중량의 블록들을 그룹화하고 한 종류의 트랜스포터를 이용하여 운반하도록 가정하여 최소의 트랜스포터 수를 구하였다. 이를 위해 Maxwell과 Muckstadt (1982), Koo, et al. (2004)이 제시한 최적화 모형을 이용하여 휴리스틱 시간(공차 운행 시간, 지연 시간 등)을 최소화하는 트랜스포터 경로 및 일정 계획 절차를 제시하였다.
Yu (2005)는 Backtracking 알고리즘을 이용하여 트랜스포터의 블록 운반 거리 및 경로에 따른 운반 시간을 최소화하는 최적 경로를 결정하였다. 하지만 이 연구는 블록의 최적 운반 순서 결정은 다루지 않았다.
Yim, et al. (2008)과 Roh and Cha (2011)는 트랜스포터의 공주행 거리 최소화를 고려한 블록 운반 계획 문제를 최적화 문제로 정식화하였다, Dijkstra 알고리즘을 이용하여 모든 블록 간의 최단 운반 거리 및 경로와 최단 공주행 거리, 경로 등의 정보를 기반으로 트랜스포터에 블록들을 할당하는 방법을 사용하였다. 개미 알고리즘(Ant Colony Optimization)을 이용하여 단일의 블록들이 주변에 가장 가까운 블록들을 집합으로 해서 각각의 트랜스포터에 운반할 블록을 할당하고, 이를 초기해 집합으로 가정한 후 유전자 알고리즘으로 블록의 운반순서를 결정함으로써 최적 블록 운반 계획을 제시하였다.
한편, Cha, et al. (2012)은 A*(A star) 알고리즘을 이용해서 트랜스포터의 교차 주행 여부를 고려하여 계산 시간을 단축하기 위한 알고리즘을 구현하였다.
Heo, et al. (2013)은 트랜스포터의 최적 블록 운송 계획을 위해 Yim, et al. (2008)과 Cha, et al. (2012)에서 제시한 최적화 모형을 이용하여 블록 운송 경로에서 트랜스포터가 고장이 날 경우, 사고가 발생할 경우, 갑자기 경로 중 일부가 PE장으로 사용이 될 경우 등에 대처할 방안을 제시하고 있다. 특히 손상 간선이 발생한 경우, 해당 간선은 트랜스포터가 이용할 수 없으므로 손상된 간선을 제외한 최단 경로를 A* 알고리즘으로 재계산하여 새로운 경로를 재탐색하도록 하는 연구를 수행하였다.
기존의 연구(Yim, et al., 2008; Cha, et al., 2012; Heo, et al., 2013)에서 블록의 최단 경로를 탐색하는 알고리즘으로는 Dijkstra, A* 알고리즘 등이 사용되었다. Dijkstra 알고리즘은 한 지점에서의 일대다 탐색으로 최단 경로를 결정하는 방법으로 출발지에서 도착지까지의 경로를 탐색할 때 출발지에서 다른 모든 절점 간의 최단 경로를 탐색한 후 도착지와의 최단경로를 알려준다(Heo, et al., 2013 cited in Dijkstra, 1959). 한편, A* 알고리즘은 일대일 탐색으로 출발지에서 도착지까지의 경로를 탐색할 때 출발지에서 인접한 절점의 간선 거리와 인접한 절점에서 도착지까지의 직선거리 합을 계산하여 최소거리 값을 가지는 절점을 확장해가면서 도착지를 탐색하는 방법이다(Heo, et al., 2013 cited in Hart, et al., 1968). Dijkstra 알고리즘처럼 불필요한 경로를 탐색하지 않고 출발지와 도착지를 일대일로 탐색하는 방법이기에 A* 알고리즘의 계산 속도는 더 빠르다. 그러나 출발 절점과 도착 절점이 비교적 많은 경우에는 모든 절점을 일대일 탐색해야 하므로 문제에 따라 오히려 계산시간이 길어지는 특징을 가지기도 한다.
Cha, et al. (2012), Heo, et al. (2013)의 연구에서는 조선소에 있는 모든 지점 간의 최단경로를 탐색하지 않고 운반할 블록들의 출발지와 도착지 간의 최단경로, 각 블록의 도착지와 다른 모든 블록의 출발지 간의 최단경로를 A* 알고리즘을 사용하여 탐색하였다. 또한, 트랜스포터의 블록 운송 경로에 손상 간선(절점)이 발생하였을 때 손상 간선을 제외한 다른 경로를 찾는 방법으로 A* 알고리즘을 이용하여 탐색하였다.
본 연구에서는 Dijkstra 알고리즘, A* 알고리즘과 Floyd 알고리즘을 사용하여 탐색하는데 걸리는 시간을 비교하였다. 또한, 손상 간선 발생으로 해당 간선을 우회하는 경로를 제시하는 즉각적인 방법이 아니고, 전체 트랜스포터 운영계획 차원에서 손상 간선 발생 및 계획 없던 블록의 추가 등에 대응할 방안을 제시하려 한다. 마지막으로 트랜스포터가 최단경로를 따라 운행 시 직선 구간과는 달리 교차지점에서는 회전시간이 발생하게 되므로, 트랜스포터 운영계획 시 트랜스포터가 회전할 때 걸리는 시간을 트랜스포터의 최소 공차 이동시간에 고려하는 실용적인 접근방법을 적용하였다. 이를 바탕으로 트랜스포터의 운영계획에서 최소 공주행 시간을 가질 수 있도록 주어진 트랜스포터들에 블록 할당 및 운반 순서를 결정하는데 전역 최적화 방법의 하나인 SA(Simulated Annealing) 기법을 사용하였다. 또한, 각각의 블록의 운반 일정 및 트랜스포터가 들 수 있는 최대 중량에 위반되지 않도록 제한조건을 적용하였다.
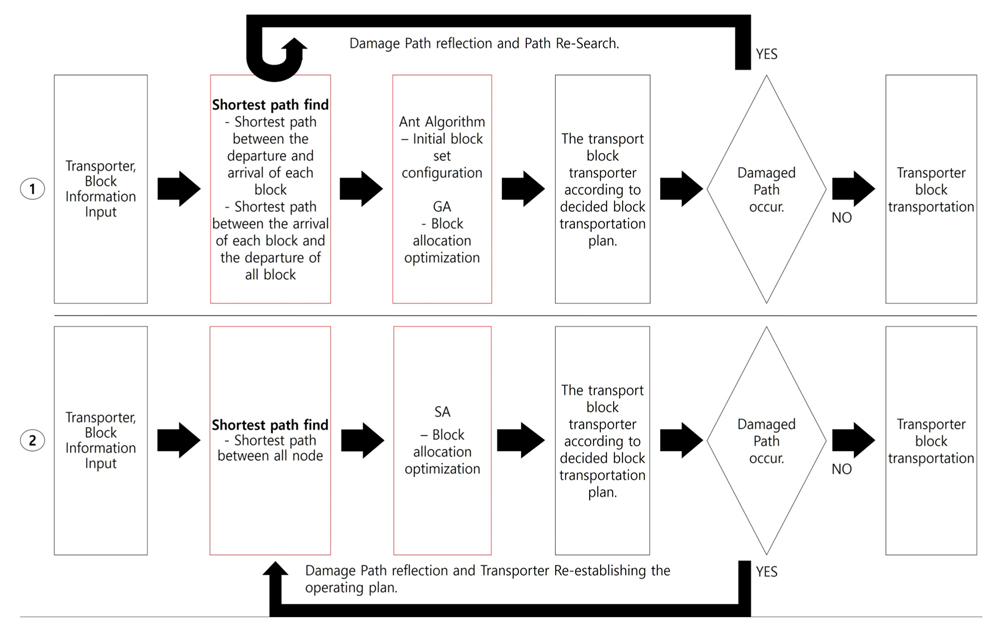
Heo, et al. (2013)은 Fig. 1의 ①과 같은 최적 블록 운송 계획 절차를 제시하고 있다. 우선 블록 운송 계획을 수립하기 전에 트랜스포터의 적재중량, 주행 및 공주행 속력, 작업 일정 등의 정보와 운반할 블록의 중량, 출/도착지의 정보, 운반 일정 등의 블록 정보, 그리고 트랜스포터가 이동하는 조선소의 경로에 대한 정보가 필요하였다. 또한, 각 블록의 출발지와 도착지 간의 최단 경로와 각 블록의 도착지와 다른 모든 블록의 출발지 간의 최단 경로를 미리 계산하는데 A* 알고리즘을 사용하였다.
다음으로 트랜스포터 별 블록 할당과 블록 운송 순서를 결정하기 위해 최적화 문제를 정의한다. 이 문제를 최적화 문제에 적용하면 목적함수는 공차 이동 시간을 최소화하도록 하면서 트랜스포터의 최소 회전을 하는 것이며(식 (1)), 제약조건으로는 운송 블록의 무게가 트랜스포터의 적재 능력보다 작아야 하며(식 (2)), 모든 블록은 운송 완료 제한 시각 내에 완료(식 (4))된다고 가정하였다. 또한, 모든 블록은 운반 시작 가능 시각 이후에 운송을 시작해야 하고(식 (3)), 우선순위에 따라 블록을 운송(식 (5))해야 한다. 이 제약조건들을 목적함수에 적용하기 위해 페널티 방법을 사용하였다. 블록의 중량과 트랜스포터의 적재능력 간의 부등식, 제한 시각과 실제 운송 시작/완료 시각 간의 부등식을 비교하여 위배하는 경우 페널티를 부여하는 방식을 사용하였다(Yim, et al., 2008). 다만 목적함수의 회전 관련 항은 본 연구에서 처음 언급된다.
Minimize
Subject to
where
GA(Genetic Algorithm)를 적용하기 전에 초기 블록 운송 계획을 수립하기 위해 개미가 자주 다니는 길에 페로몬을 남기는 것에 착안하여 가상 개미를 주행시키는 휴리스틱 최적화 방법인 개미 알고리즘(Ant Colony Optimization)을 사용하였고, 그 다음 GA(Genetic Algorithm)를 수행하여 최종 블록 운송 계획을 수립하게 한다. 위의 과정을 통해 결정된 블록 운송 계획에 따라 트 랜스포터를 운행을 하게 되는데, 이때 운송 도중 운송 경로에 문 제가 발생할 경우, 계산 비용이 극도로 많이 소비되는 운영계획 전반을 다시 수행하는 것이 아니고, 손상된 간선을 포함하는 트 랜스포터들의 최단 경로만을 다시 재설정하는 과정을 거친다 (Heo, et al., 2013).
본 논문에서는 Fig. 1의 ①과는 다르게 임의 지번의 임의 블록이 추가되는 경우, 불시에 발생한 사고로 손상 간선이 발생할 경우 그리고 일정 경로가 적치장으로 변경 운영되는 경우 등에 대비하기 위해서 조선소에 있는 모든 절점 간의 최단 경로를 先 탐색을 한다. 비교에 참여한 최단경로 탐색 알고리즘으로는 Dijkstra 알고리즘, A* 알고리즘, Floyd 알고리즘 등이며 최단 경로를 탐색하는 시간을 비교하여 본 논문에서 제시한 시나리오를 적용해보았다. 또한 ②에서 볼 수 있듯이, 이미 탐색 된 블록의 이동 경로만을 대상으로 손상된 경로만을 피해 가는 방법에서 탈피하여, 전반적인 경로들을 모두 재탐색하고 이를 운영계획에 반영하는 방안을 택하였다.
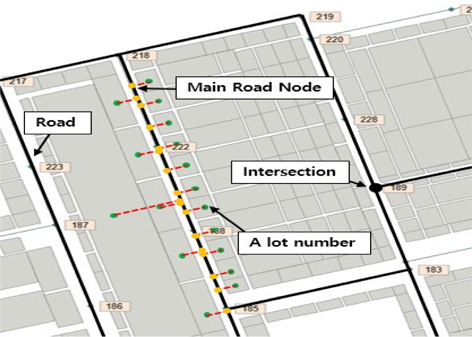
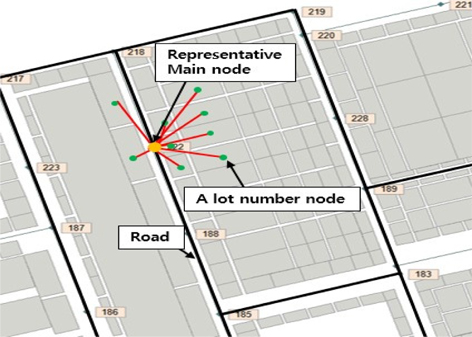
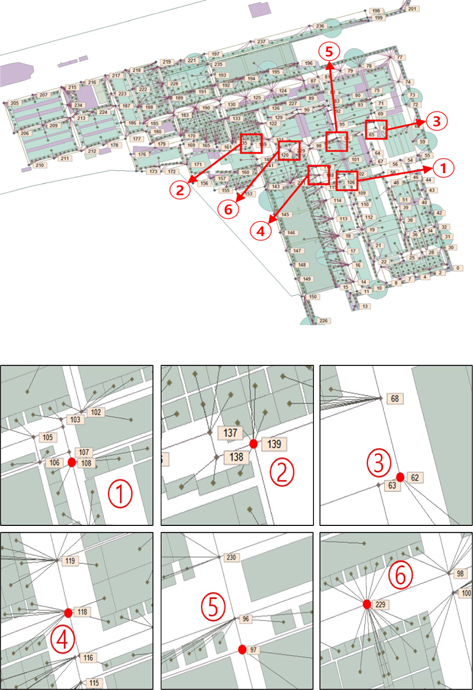
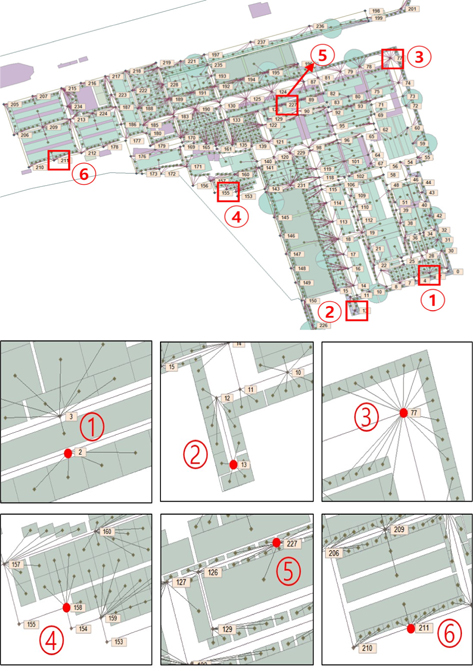
수치실험에 활용한 조선소 안에 있는 지번에 수는 총 1,596개로 이 지번 안에 있는 로컬노드(지번 노드)의 개수와 같으므로 이에 일대일로 대응하는 메인도로의 노드 수 또한 1,596개 이다. 하지만 교차로의 존재하는 노드를 합하면 메인도로의 총 노드 수는 더 증가하게 된다. 계산에 사용되는 노드 수의 증가는 알고리즘의 수행시간에 크게 영향을 줄 수밖에 없다. Fig. 2와 같이 노드를 연결하였을 경우 약 1600여 개의 노드를 통해 이동경로를 탐색하게 되는데, 본 논문에서는 Fig. 3에서처럼 지번에 있는 절점은 그대로 사용하고 지번에 있는 절점과 연결된 메인도로에 대표 주요절점을 지정하여 로컬노드와 메인도로의 대표 노드를 다대일로 연결하여 알고리즘의 계산에 사용되는 노드의 수를 약 85% 줄였다. 메인도로에 위치한 대표 절점의 수와 도로의 교차지점 절점 수의 총 개수는 238개이며, 238개 절점 간의 최단경로를 탐색하는데 절점 간의 최단거리를 비교하고 걸리는 시간을 비교하였다.
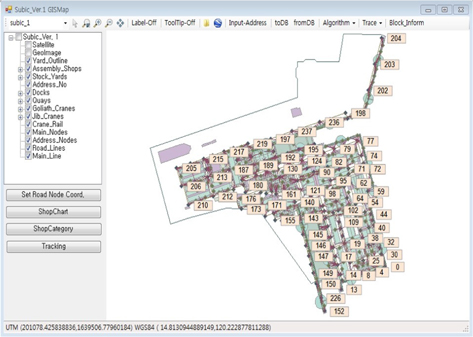
H사의 조선소 야드 정보를 바탕으로 Ruy, et al. (2015)에서 개발된 조선 전용 GIS(Geographic Information System)(Fig. 4)를 통해 트랜스포터가 운행 가능한 주도로와 주변에 가까운 위치에 있는 지번(적치장, PE장, 각종 조립장 등)과 연결하는 대표 주요절점을 지정하였다. 이 대표 주요 절점 간의 최단경로를 구한다면 대표 주요절점과 연결되어있는 지번까지의 최단경로를 확보할 수 있다고 가정하였다.
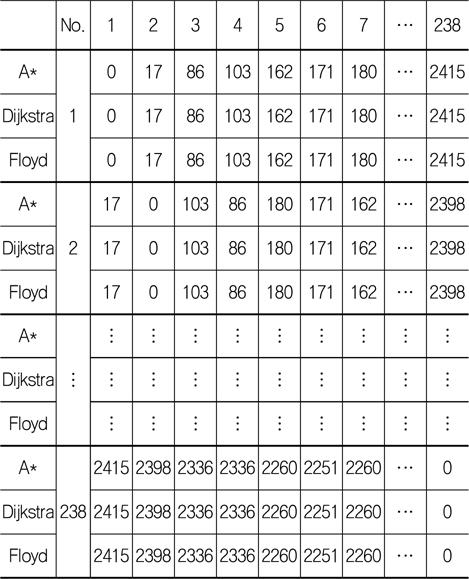
3종의 알고리즘을 수행하였을 때 대표 주요절점 간의 최단경로가 같은지를 확인해야 하는데, 이를 판단할 방법으로는 두 가지가 있다. 첫 번째는 모든 경로가 같은지 비교하는 것이고, 두 번째는 절점(node) 간의 최단거리가 같은지를 확인하는 것이다. 첫 번째 방법은 경로의 개수가 너무 많아 비교하는 데 어려움이 있어서 두 번째 방법인 모든 절점 간의 최단거리에 대한 자료구조를 만들어 일치하는지 비교할 수가 있다. 기존의 논문에서 최단경로를 탐색하는 데 사용한 Dijkstra 알고리즘, A* 알고리즘과 추가로 Floyd 알고리즘을 적용하여 모든 절점 간의 최단거리를 자료구조로 만들어 비교한 결과 Table 1과 같이 모든 절점 간의 최단거리가 같다는 것을 볼 수가 있었다.
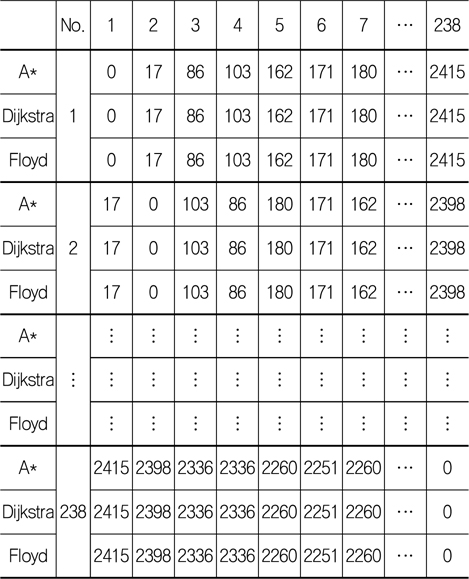
Comparison of the shortest distance between all addresses using Dijkstra vs A* vs Floyd Algorithm
Dijkstra 알고리즘은 P개의 절점과 E개의 간선으로 이루어진 그래프에서 하나의 출발지와 출발지를 제외한 다른 모든 절점 간의 최단 경로를 구하는 알고리즘이다 (Heo, et al., 2013 cited in Dijkstra, 1959). A* 알고리즘은 하나의 출발지와 하나의 도착지 간의 일대일 최단 경로를 계산하는 알고리즘이다 (Heo, et al., 2013 cited in Hart, et al., 1968). Floyd 알고리즘은 N개의 절점으로 구성된 방향 그래프에서 각 절점을 출발 절점으로 하여 모든 절점 쌍 사이의 최단경로를 구하는 방법으로 All-To-all 문제 해결의 가장 효율적인 방법으로 알려져 있다 (Lee, et al., 2009).
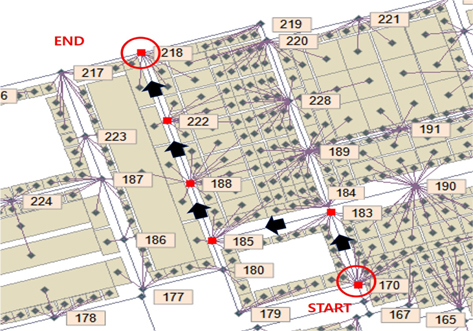
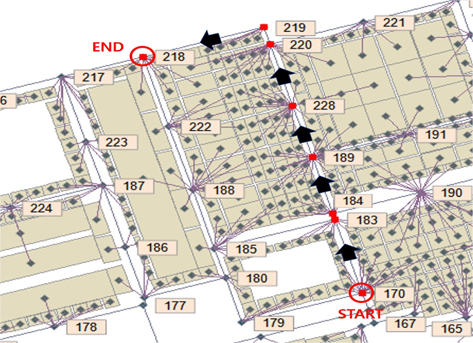
Fig. 5와 Fig. 6을 보면 출발지 170번 절점과 도착지 218번 절점이 같은데 이동 경로가 다른 것을 볼 수가 있다. Fig. 5는 Dijkstra 알고리즘과 Floyd 알고리즘을 적용한 것이고, Fig. 6은 A* 알고리즘을 적용한 것이다. Fig. 5와 Fig. 6에서 출발지와 도착지 간의 실제 이동 거리(manhattan distance)는 같지만 경로가 다른 것을 볼 수가 있다. Fig. 5, Fig. 6에서 183번 절점에서 도착지 218번까지 이동하는 최단 경로는 219번을 경유하거나 222번을 경유하나 같은 거리이다. 같은 거리를 가지는 218번까지의 경로가 Dijkstra 알고리즘(Floyd 알고리즘)과 A* 알고리즘 탐색에 서 다른 결과를 보여주고 있다. 이는 Dijkstra 알고리즘은 한 절점을 기준으로 인접 절점 간의 최단거리가 경로설정의 기준이 되 기 때문이다. Fig. 6은 170번 절점에서 218번 절점까지의 최단 경로를 A* 알고리즘을 이용하여 탐색하는데 170번 절점에서 연결되어있는 다음 절점은 179번 절점과 183번 절점이다. 179번 절점으로 이동하여 218번 절점과의 직선거리를 더한 값과 183번 절점으로 이동하여 218번 절점과의 직선거리(heuristic distance)를 더한 값을 비교하여 더 작은 값을 가지는 절점으로 이동한다. A* 알고리즘을 이용한 경로 탐색에서는 휴리스틱 거리가 교차지점에서의 경로 방향을 결정하는 중요한 정보가 된다. 따라서 183번 절점과 연결되어있는 184번 절점과 185번 절점의 위치에 따라 경로 방향이 달라질 수가 있다. 이렇게 같은 방법을 계속 수행하면 도착지인 218번 절점에 도착하게 된다. 결국, 손상 경로가 없어 모든 경로가 격자로 완벽하게 통과 가능한 수치 지도의 경우, 이동 거리 관점에서는 3종 알고리즘이 같은 결과를 산출함을 알 수 있었지만, 알고리즘이 가지는 차이점 때문에 경로에 차이점이 발생할 수 있음을 확인하였다. 트랜스포터의 최단 경로의 문제는 단순히 거리로만 평가될 수 있는 문제는 아니다. 교차로에서 안전 확보 시간, 회전에 필요한 시간 등을 환산하여 알고리즘에 반영한다면 위에서 제시한 두 경로 간에도 우열이 발생할 수 있으며 이 문제는 6장에서 서술한다.
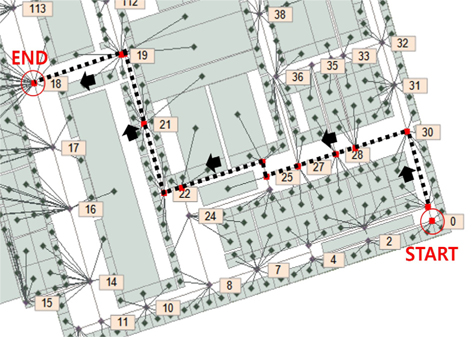
Fig. 7은 손상된 절점이 없는 경우, 0번 절점에서 18번 절점까지의 Dijkstra 및 A* 알고리즘을 사용한 최단경로이다.
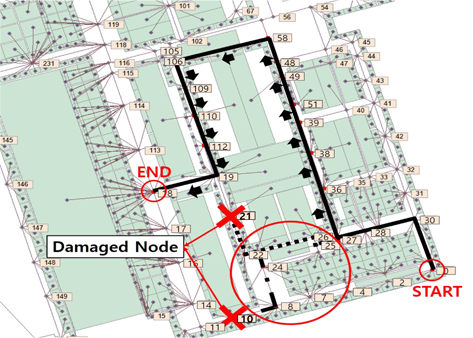
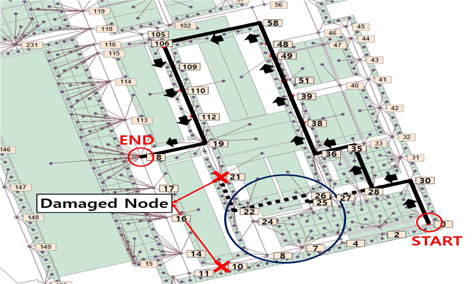
Fig. 8은 10번, 21번 절점이 손상된 절점으로 가정하고 0번 절점에서 18번 절점까지의 최단경로를 A* 알고리즘으로 탐색하는 과정을 보여주고 있다. 먼저 0번 절점에서 출발하여 Fig. 7에서 보이는 점선의 경로와 같이 손상된 21번 절점 직전까지 탐색하게 되는데, 21번 절점이 손상되었기 때문에 다음 최단거리 값을 가지는 10번 절점이 있는 방향으로 경로를 탐색한다(일점쇄선). 그런데 10번 절점 직전까지 이동해야 10번 절점이 손상되었다는 것을 알게 되어 다시 새로운 경로(화살표 실선)를 탐색하게 된다. 화살표를 따라 18번 절점에 도착하게 되면 결과적으로 0번 절점에서 18번 절점까지의 A* 알고리즘의 최단경로는 실선의 경로가 출력된다. Fig. 9는 Fig. 8에서처럼 10번, 21번 절점을 손상된 절점으로 반영하여 Dijkstra 알고리즘으로 탐색하였는데, 손상 절점이 노드 간 거리 Table 구성에 직접적인 영향을 주어 경로탐색과정에서 Fig. 8과는 다르게 바로 도착지와의 최단경로(실선)를 탐색하게 된다. Fig. 8(실선), Fig. 9(실선)가 서로 다른 경로를 보여주고 있지만 앞서 Fig. 5, Fig. 6에서 설명했듯이 이동 거리(manhattan distance) 관점에서는 서로 같다고 볼 수가 있다. A* 알고리즘의 경우(Fig. 8), 알고리즘의 특성상 손상된 경로를 제거한 갱신된 경로로 탐색이 이루어지더라도 손상 직전까지의 경로는 다를 수가 없으며, Dijkstra 알고리즘(Fig. 9)과 달리 불가피한 우회가 발생할 수 있음을 보여주고 있다. 여기서 A* 알고리즘의 경우 손상이 발생한 경로를 탐색하는 경우 계산 비용은 비례하여 증가할 수밖에 없음을 확인하였지만, 그 외 알고리즘의 경우 경로의 단순화로 인해 계산 비용 측면에서 유리해 짐을 알 수 있다. 다음은 3종 알고리즘의 계산 비용 측면에서의 비교를 수행하였다.
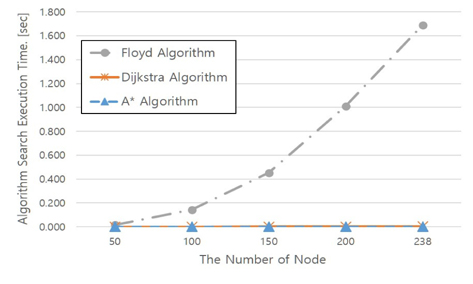
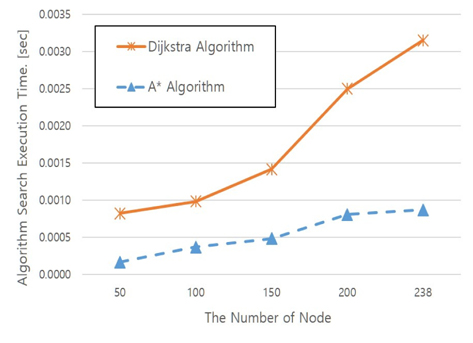
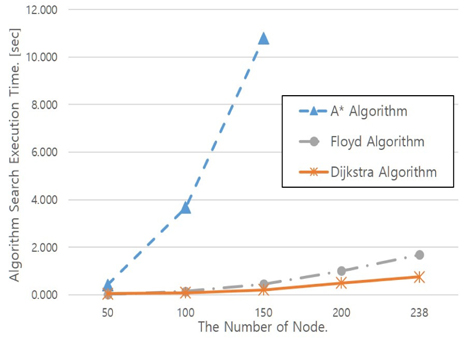
Fig. 10은 일대일 최단경로 탐색 시 시간을 비교한 것으로 Floyd 알고리즘은 3중 반복 알고리즘의 한계로 A*와 Dijkstra보다 계산 비용이 현저하게 많이 소비되어 큰 차이를 보인다. Floyd 알고리즘을 제외한 다른 두 알고리즘의 탐색 시간을 비교해보면 Fig. 11에서처럼 A* 알고리즘이 일대일 최단 경로 탐색에 소요되는 시간은 더 빠른 것을 확인할 수 있다. Fig. 12는 다대다 최단경로 탐색 시 소요되는 시간을 비교한 그래프이다. Fig, 10, Fig, 11, Fig, 12를 통해 절점 수에 따른 알고리즘의 계산 시간을 비교하였을 때 다대다 탐색의 경우 A* 알고리즘은 일대일 계산을 n²번 해야 하므로 n번 계산하는 Dijkstra 알고리즘보다 느려짐을 확인할 수 있다. 이러한 결과는 모든 문제의 계산 비교의 것으로 일반화하기 어렵지만, 절점 간을 연결하는 간선의 수가 비교적 적은 조선 수치지도를 반영한 트랜스포터의 경로탐색 문제에서의 결과임을 밝힌다. 최단경로를 찾는 시간을 비교하여 모든 절점에서의 탐색시간(다대다 탐색 소요시간)은 Dijkstra 알고리즘이 가장 빠르고, 일대일 탐색에서는 A* 알고리즘이 가장 빠른 것을 확인하였다.
따라서 본 논문 2.1절에서 제시한 시나리오를 적용한 경우에는 Fig. 12에서 볼 수 있듯이 Dijkstra 알고리즘이 가장 빠른 경로탐색시간을 보여주기 때문에 Dijkstra 알고리즘이 경로탐색 알고리즘으로 가장 적합하다고 볼 수 있다.
다음은 운송경로 중 손상된 경로가 발생 시 이를 반영하여 알고리즘을 재수행하는 시간을 비교하였다.
5. 운송경로의 손상에 따른 알고리즘 재탐색 시간 비교
조선소에서는 특정 지번과 연관된 도로가 적치장으로 사용되거나 장애물의 발생 또는 특정한 상황이 발생하여 해당 도로를 사용하지 못할 경우, 즉 손상된 도로(간선)에 의해 블록 운송 경로를 변경해야 하는 상황이 발생할 수 있다. 손상 간선에 의한 경로 변경을 블록 운송 계획에 적용시켜 계획을 재수립하는 데 사용되는 Dijkstra 알고리즘과 A* 알고리즘의 경로 재탐색 수행 시간을 비교하였다.
Fig. 13, Fig. 14는 100개의 블록 정보(Fig. 21)를 입력하여 블록의 최단 운반 경로와 최단 공차 이동 경로를 결정하였을 때, 각 절점의 트랜스포터 통과 횟수 분석 결과를 보여준다. Fig. 13은 통과 횟수가 상위 10%인 절점들의 위치이고 Fig. 14는 하위 10%인 절점들의 위치이다. Fig. 13, Fig. 14에 표시된 절점들을 이동할 수 없는 절점, 즉 손상된 절점으로 가정하였다. 이러한 절점들을 손상 절점으로 정한 이유는 손상된 절점의 트랜스포터의 통과 빈도수에 따라 갱신해야 하는 경로의 수가 최단 경로 탐색에 사용되는 알고리즘의 계산비용을 지배할 것이라 예상했기 때문이다.
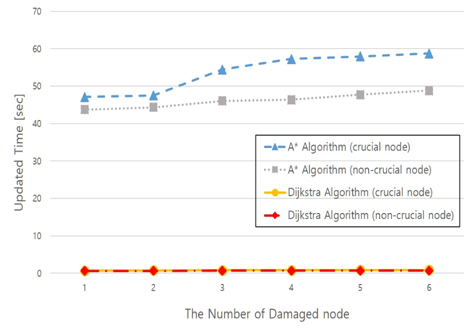
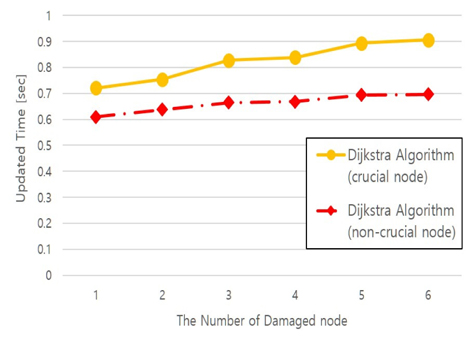
Fig. 15는 Fig. 13, Fig. 14에서 표시된 절점을 손상된 절점으로 가정한 후 손상된 절점 개수의 따른 Dijkstra 알고리즘과 A* 알고리즘의 경로 재탐색 시간을 비교한 것이다. Fig. 15에서 중요 절점과 비중요 절점에 대한 A* 알고리즘 그래프를 보면 비중요 절점을 대상으로 하는 재탐색 시간이 더 빠른 것을 볼 수가 있다. 또한, 모든 절점 간의 최단경로 재탐색이기 때문에 4.1장에서 언급하였듯이 Dijkstra 알고리즘이 A* 알고리즘에 비해 빠른 재탐색 시간을 보여준다. Fig. 15에 중첩되어 보이는 Dijkstra 알고리즘에 대한 중요, 비중요 손상 절점 경로 재탐색시간의 차이는 Fig. 16에서 확대하여 볼 수 있다. 손상된 절점(중요, 비중요)이 포함되어있는 경로를 찾는 시간의 차이가 재탐색 시간에 영향을 주고 있는 것을 Dijkstra 알고리즘에서도 볼 수 있다.
손상이 없는 경로의 탐색에서 Dijkstra 알고리즘과 A* 알고리즘의 경로는 때에 따라 미세한 차이가 있을 수 있지만, 이는 탐색하는 방법에 따른 차이일 뿐 도착지까지의 최단거리는 같다는 것을 확인할 수 있다. Fig. 12와 Fig. 15에서 볼 수 있듯이 모든 절점 간의 최단경로를 탐색하는 시간(다대다 탐색 소요시간)에서 Dijkstra 알고리즘이 A* 알고리즘보다 우수함을 알 수 있다. 다음은 본 연구에서 제시한 운영 계획 수립에 Dijkstra 알고리즘과 A* 알고리즘을 적용하여 비교한다.
6. 트랜스포터가 회전하는데 소요되는 시간을 고려한 최단 공차운행경로
트랜스포터는 보통 운전기사 1명과 신호수 4명이 한 조가 되어 운행하며, 신호수는 블록의 사방 모서리에서 전, 후, 좌, 우 주위 벽면에 간섭이 생기지 않는지 확인하고, 맞은편에서 오는 차량 또는 사람들을 대피시키는 역할을 한다. 이처럼 트랜스포터 운행은 많은 작업자가 필요할 만큼 위험도가 높기 때문에 도로의 교차지점 또는 코너에서 회전시간이 많이 소요되므로, 회전구간 이 많을수록 트랜스포터가 도착지에 도착하는 시간은 증가하게 된다. 회전을 고려하여 최단경로를 탐색하는 방법으로는 알고리즘 내에서 최단경로를 탐색하는 과정에서 회전을 고려하는 방법과 최단경로를 탐색하고 난 후, 적은 회전을 추구하는 경로를 선택하는 방법이 있다. 경로탐색과정에서 회전을 고려하여 최단경로를 탐색하는 방법에서 Dijkstra 알고리즘은 Bellman의 최적원리를 기본 개념으로 적용하기 때문에 실제 도로 교차로에서 좌회전, 우회전할 때 발생하는 회전시간을 고려하지 못하는 단점이 있다(Yang, 2000). 본 연구에서는 운영계획 알고리즘에 회전 최소화 경로 선택 방안에 관해서 연구를 집중하였다.
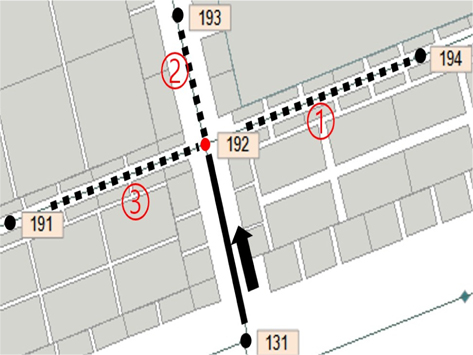
먼저 교차로에서의 회전하는 시간을 계산하는 방법으로는 Fig. 17에서 131번 노드에서 192번 노드로 이동했을 때 192번 노드를 중심으로 194번 노드와 연결된 ①번 도로, 193번 노드와 연결된 ②번 도로, 191번 노드와 연결된 ③번 도로가 있다. 131번 노드에서 192번 노드가 있는 교차로로 들어왔을 때 192번 노드를 중심을 194번, 193번, 191번 노드와 131번 노드와의 벡터내적 계산을 통해서 회전 유무를 판단하였다.
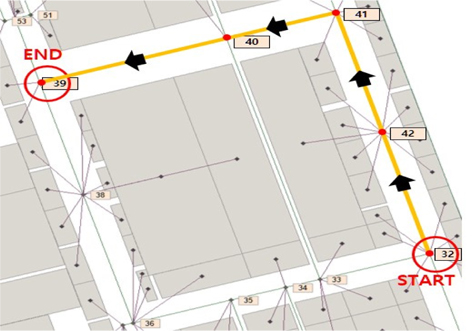
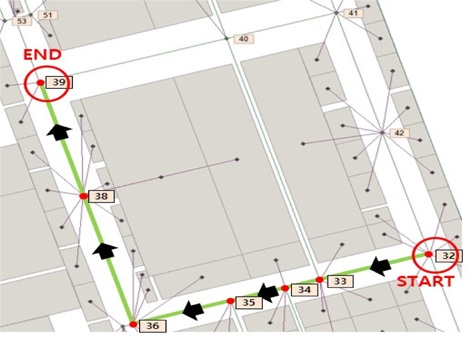
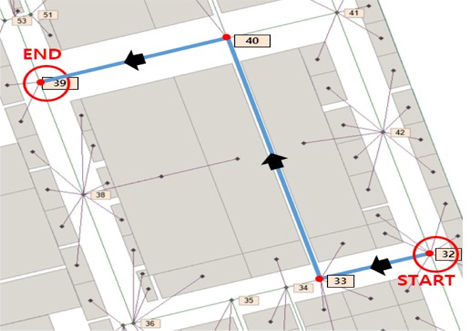
간단히 예를 들어 Fig. 18, Fig. 19, Fig. 20에서 보면 32번 절점에서 출발하여 39번 절점에 도착하는 각각 다른 경로 3개를 볼 수 있는데, 총 이동 거리는 동일하다.
첫 번째로 Fig. 18의 경로는 41번 절점에서 트랜스포터의 회전이 한번 이루어지고 40번 절점(도로 교차지점)에서 감속을 하게 된다. 두 번째로 Fig. 19의 경로는 33번, 34번, 35번 절점(도로 교차지점)에서 감속하게 되고, 36번 절점에서 회전을 한번 하게 된다. 마지막으로 Fig. 20의 경로는 33번과 40번 절점에서 회전이 각각 한 번씩 이루어진다.
Dijkstra 알고리즘은 회전을 고려하지 못하기 때문에 3개의 경로 모두 최단경로가 된다. 하지만 트랜스포터의 회전과 감속 후 다시 운행하는데 걸리는 시간에 페널티 차이를 주어 최단거리 계산에 적용하면 최단경로는 Fig. 18(32번 → 42번 → 41번 → 40번 → 39번)이다. 이와 같은 방법을 이용하여 트랜스포터 운영계획 수립 시 공차운행경로를 결정하는데 적용하였다.
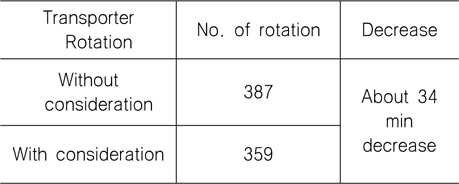
Table 2는 트랜스포터의 회전을 고려하지 않았을 때와 고려하였을 때 공차 이동 경로에서 트랜스포터의 회전 횟수를 비교한 것이다. 회전을 고려하지 않았을 때는 총 공차 이동 경로에서 트랜스포터의 회전 횟수가 387번이고, 회전을 고려하였을 때는 359번으로 회전 횟수의 차이는 28번이다. 이를 회전하는데 걸리는 시간으로 계산하였을 때, 예를 들어 트랜스포터의 공차 상태 회전 평균속도가 5 km/h이고, 한번 회전할 때 100 m씩 거리가 늘어나는 페널티를 적용하면 28번 회전을 하지 않을 경우 약 34분의 시간이 감소하게 되는 것이다.
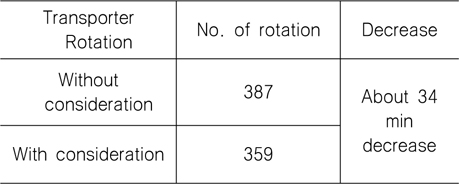
The total vacant transport path comparison of the number of rotations after planning considering the rotation
7. Simulated Annealing을 활용한 트랜스포터 운영 계획
지금까지 블록 운송 계획을 세우기 전 각각 블록의 출발점과 도착지점 간의 최단거리를 구하여 블록이 이동하는 최단경로를 주로 언급하였다. 다음은 실제 블록 운송 정보와 트랜스포터 운영 정보를 입력하여 트랜스포터의 최적 운영계획을 수립하였다.
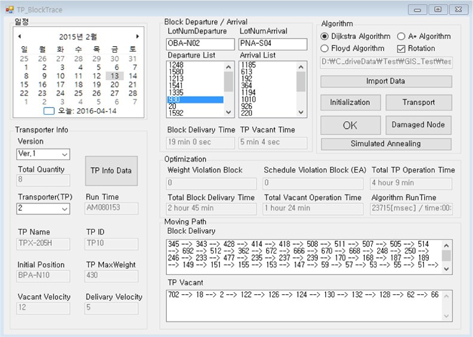
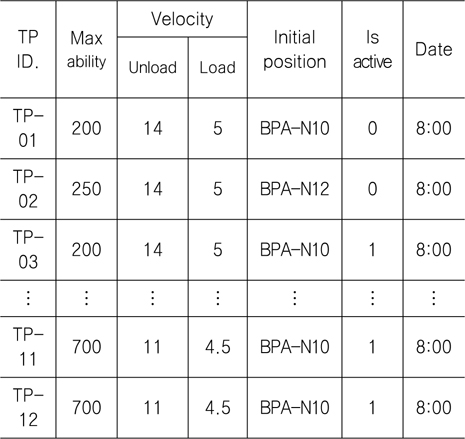
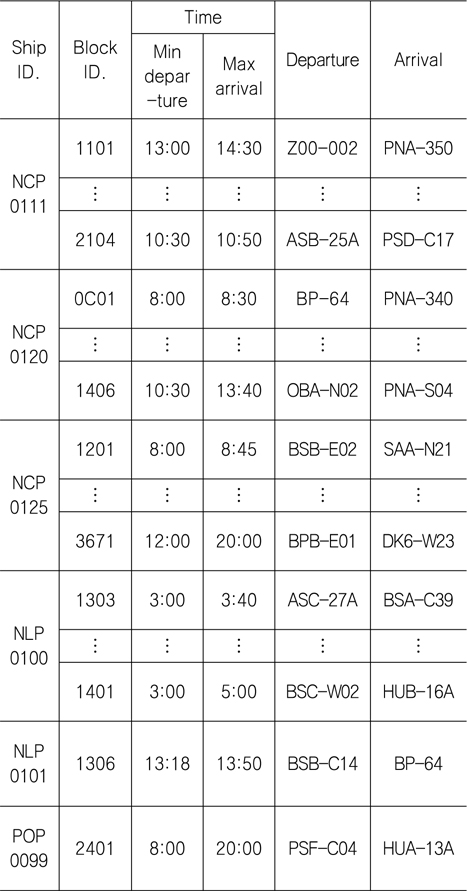
Table 3, Table 4는 본 논문에서 적용한 8개의 트랜스포터의 운행 정보와 2015년 2월 13일에 운송한 100개의 블록 정보이다. 트랜스포터 정보에는 트랜스포터가 운반할 수 있는 최대 중량과 운행속도, 운행가능여부, 운행 시작 시간 등이 있다. 블록 정보에 는 출발지점, 도착지점, 최소 출발시각, 최대 도착시각 등이 나열되어있다. 이 정보를 가지고 트랜스포터가 어떤 블록을 할당받느냐에 따라 트랜스포터의 최적 운행 계획이 수립되게 될 것이다. 트랜스포터의 최적 블록 운송 계획을 세우는 목적은 트랜스포터의 하루 주행 시간을 줄이는 데 있다. 블록을 운반하는 시간은 트랜스포터가 움직이는 시간이므로 고정되어있다고 볼 수 있다. 하지만 블록을 운반한 후 싣지 않은 상태에서 다음 블록이 있는 곳까지 이동하는 공차 이동 시간은 다음 블록의 선택에 따라 달라질 수 있다. 결국, 트랜스포터의 총 공차 이동 시간을 줄이는 것이 최적 블록 운송 계획을 수립하는 것이다.
[Table 3] Transporter data of a shipyard
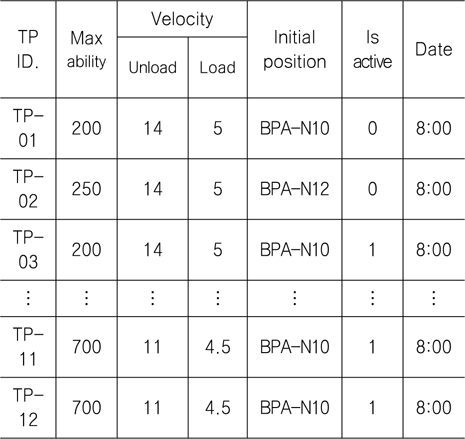
Transporter data of a shipyard
[Table 4] Block transportation data of a shipyard
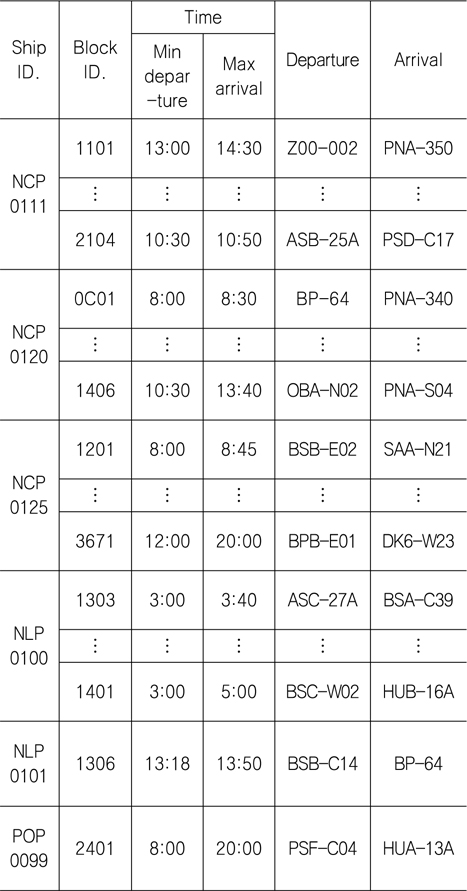
Block transportation data of a shipyard
Fig. 21은 Table 3, Table 4의 트랜스포터 운행 정보와 블록 정보를 입력받아 SA(Simulated Annealing)를 이용한 최적화를 수행한 후의 트랜스포터의 블록 운반 최단경로와 공차운행 최단 경로를 보여주고 있다.
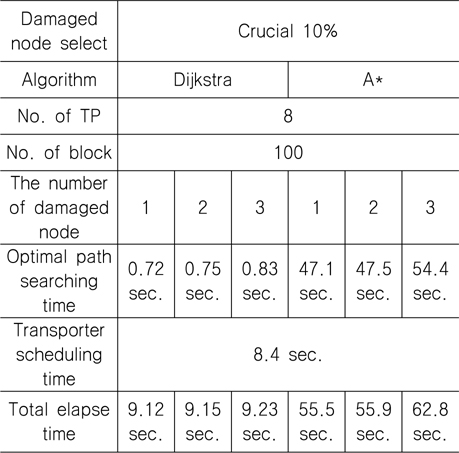
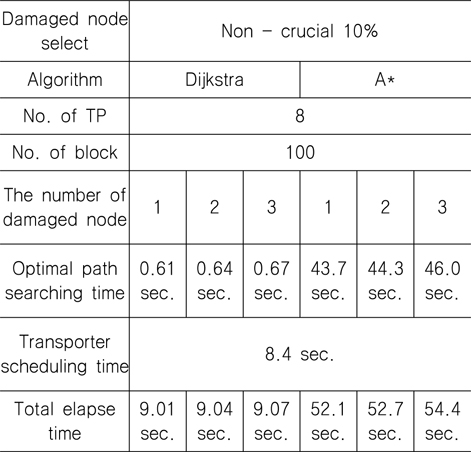
통과 빈도수가 상위 10%, 하위 10%인 절점을 손상된 절점으로 가정하고 SA(Simulated Annealing)를 통해 A* 알고리즘과 Dijkstra 알고리즘의 계산 소요시간을 비교해 보면 상위 10%의 경우, Table 5에서 볼 수 있듯이 총 계산시간이 Dijkstra 알고리즘이 A* 알고리즘보다 약 84% 감소하는 것을 확인할 수 있다. 하위 10%의 경우, Table 6에서 보면 Dijkstra 알고리즘이 약 83%만큼 감소한 것을 확인할 수가 있다. SA(Simulated Annealing)를 통해 도출된 트랜스포터의 운영계획은 제시하였던 모든 구속 조건을 만족함을 확인할 수 있었다.
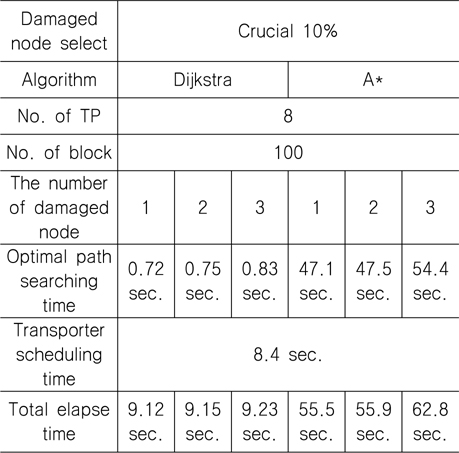
Results of the optimum block transportation simulation considering the top(10%) ranked crucial damaged nodes
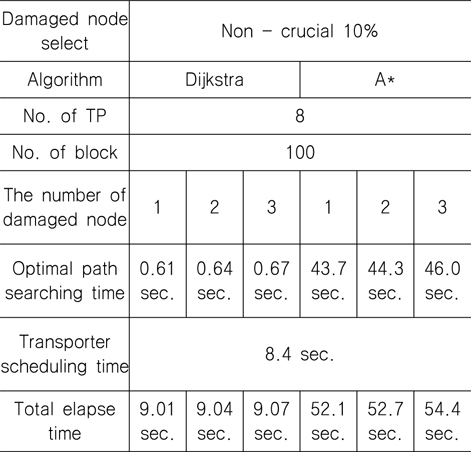
Results of the optimum block transportation simulation considering the bottom(10%) ranked non-crucial damaged nodes
본 연구에서 경로 탐색 기법 중에 Dijkstra, A*, Floyd 알고리즘들의 계산 비용과 정밀도를 검증하였다. 사용되는 문제의 종류와 분야에 따라 장단점이 존재할 수 있음을 확인하였지만, 본 연구에서 제시하는 트랜스포터 운영계획 시나리오에서의 가장 적합한 경로 탐색 기법은 Dijkstra 알고리즘임을 확인하였다. 트랜스포터가 회전 시 소요되는 시간을 탐색 된 공차 이동 경로에 적용하여 최단 공차 이동 경로를 찾을 수 있도록 하였다. 회전을 고려하지 않을 때와 고려하였을 때의 총 공차 이동 시간이 단축된 것을 확인할 수 있었다. 그리고 손상된 경로를 반영하여 운영 계획을 실시간으로 새롭게 업데이트하는 경우에도 해당 알고리즘의 계산 비용적 및 합리적인 경로 탐색이 A* 알고리즘보다 뛰어남을 확인할 수 있었다. 계산 비용적 특징을 차치하더라도 A* 알고리즘의 휴리스틱 탐색 특성은 손상 경로 탐색의 전역적 최적화 경로를 방해하는 면이 있으며, 본 연구에서 제시하는 가변적 환경에 적합한 트랜스포터 운영계획 시스템에서는 존재하는 모든 지번을 대상으로 최단 경로를 탐색하는 특징을 가지므로 Dijkstra 알고리즘의 시간적 탐색 효율성이 꼭 필요하였다.
종합해 보면, 조선 야드의 블록 물류 이동은 정적인 환경이 아니고 다양한 경우와 사고에 유연하게 대처해야 한다. 본 연구에서는 이를 위해서 미리 모든 지번 간의 최단 경로의 확보가 필요하였고 이를 실시간으로 반영할 수 있는 트랜스포터의 운영계획 시스템을 구축하였으며, 가장 적합한 경로 탐색 알고리즘은 Dijkstra 알고리즘이었다.