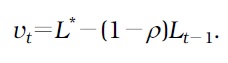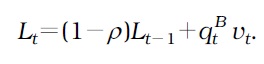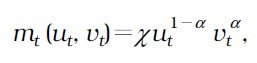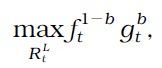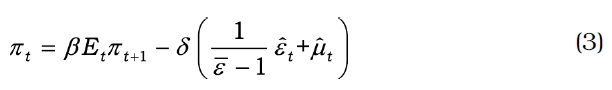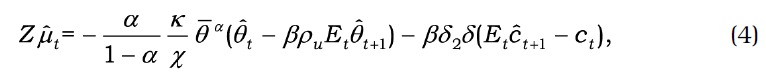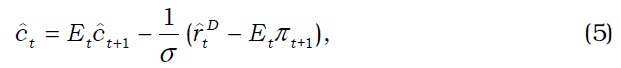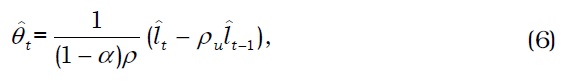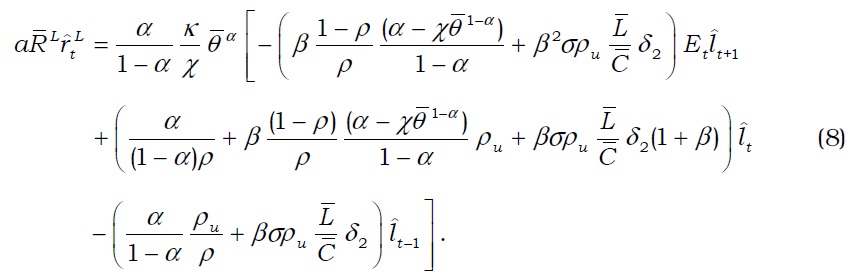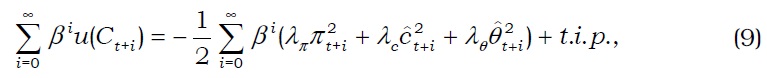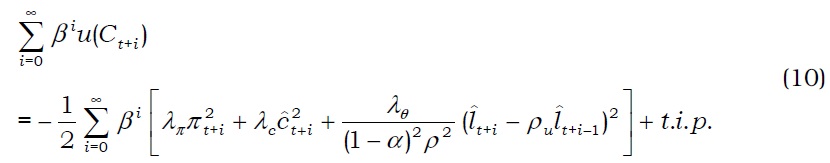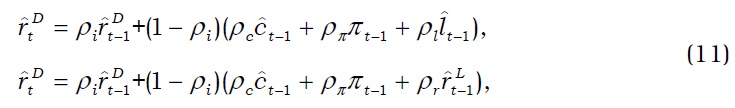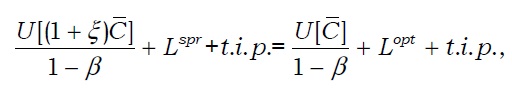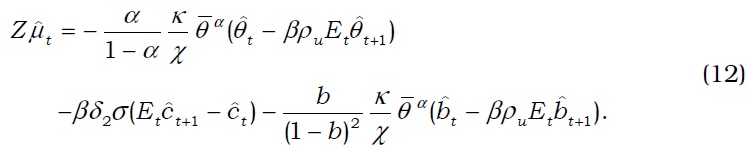Given the limits of the current policy framework, which include monetary and fiscal policies in the financial crises of the last decade, policy makers have searched for new macro policy to avoid crisisand mitigate large disruption in a crisis. Macroprudential policy is a strong candidate for the new macro policy. The new policy aims to control the behavior of banks such as lending and achieves stability in the entire financial system.

In practice, some international organizations have introduced macroprudential policy, such as the Basel III framework (Basel Committee on Banking Supervision (BCBS 2010, 2014). Under the Basel III framework, banks are required to satisfy a certain base level of capital ratio against risky assets to stabilize the volume of loan, and this base changes according to economic and financial conditions. Several countries have also introduced several types of macroprudential policies, including total credit control and capital control, as described in Lim et al. (2011) and Nier et al. (2011).

Some studies evaluate the roles of macroprudential policy using theoretical models including dynamic stochastic general equilibrium (DSGE) models. Schmitt-Grohe and Uribe (2012) develop a small open economy in which downward nominal wage rigidity pegging he nominal exchange rate induces a pecuniary externality. They show that under such an environment, the Ramsey optimal capital controls act as prudential policy in the sense that they tax capital inflows in good times and subsidize external borrowing in bad times. Eventually, this macroprudential policy reduces the average unemployment rate and average external debt, and increases welfare under reasonable parameters.

Quint and Rabanal (2011) assume a new Keynesian type DSGE model with real, nominal, and financial frictions; they study the optimal combination of monetary and macroprudential policies. They numerically show that the social welfare improves when the objective of the policy maker includes the credit term, which implies that the macroprudential policy is relevant. Suh (2012) shows that to improve welfare, macroprudential policy should respond to credit, whereas monetary policy should respond to the output gap and the inflation rate using the DSGE model with real, nominal, and financial frictions.

In this paper, we first develop a model with financial frictions by search and matching between firms and banks in the loan market as proposed by Fujimoto et al. (2014). Following Fujimoto et al. (2014), we review the reason why simple monetary and macroprudential policy rules need to include financial variables such as volume of credit and rate of loan to obtain welfare gains. We then calibrate the model for South Korea and investigate the simple and optimal monetary and macroprudential policy rules including financial variables in addition to the consumption gap and inflation rate as explanatory variables. We compare the performances of a standard Taylor rule and these optimal rules. We also verify the sensitivity for simulation by modifying the maturity of loan contracts and the range of search parameters.

The rest of the paper is organized into sections. We formulate the model in Section II. In Section III, we show the optimal criteria for policy. In Section IV, we show numerical examples of simple and optimal monetary/macroprudential policies for the Korean economy. Section V concludes the paper.

We exactly follow the model of Fujimoto et al. (2014). The full description of this model is shown in the Appendix. The economy is populated by four types of private agents, namely, a single representative household (consumer) and a large number of wholesale firms, banks, and retail firms.

An infinitely lived representative household derives utility only from consumption, such that

where σ is the coefficient of relative risk aversion. In period t, the household enjoys total consumption C_t and receives Π_t as a lump-sum profit from firms and banks. In addition, the household deposits D_t in a bank account is repaid at the end of period t with a nominal interest rate －1, where is set by the central bank. The household maximizes its utility to optimally choose total consumption C_t and deposits D_t.

In any period, a wholesale firm can either be a productive firm or a credit seeker firm. To be productive, a firm must first obtain credit a from a bank to finance the cost of production. A productive wholesale firm produces Z units of wholesale goods using inside labor with compensation a, and the labor in the productive wholesale firm consumes differentiated retail goods after production of retail goods as the consumer.

The credit market is characterized by search frictions, and a credit seeker firm must purchase retail goods κ as the consumer in each period. In period t, with probability , a credit seeker firm is matched with a bank and engages in a credit contract. Then, the firm receives a real units of credit and becomes productive, sells the produced goods to the retail firms, and repays a to the bank, in which the loan interest rate －1 is determined in equilibrium. Finally, at the end of period t, a credit contract is exogenously terminated with probability ρ ∈(0, 1), in which case the firm and the bank separate and search for new matches in period t＋1. With probability 1－ρ, a credit contract is sustained and the firm again receives credit in period t＋1. We denote ρ as the credit separation rate. We assume that free entry into the wholesale goods industry exists.

Banks post credit offers and search for credit seeker firms. We call these credit offers as “credit vacancies.” Posting credit vacancies is costless, but the total funds available for lending is fixed at aL^*, such that the upper limit of the number of credit contracts is L^*. Therefore, the number of credit vacancies v_t using L_t－1 is expressed as

A credit vacancy is filled with probability . Then, L_t is expressed as

Credit market tightness is defined as

where u_t is the number of credit seeker firms.

Retail firms produce differentiated retail goods from the wholesale good, which are then sold to the household. Wholesale firms are in a monopolistically competitive market. One unit of wholesale goods, whose price is , is converted into one unit of retail good j. To introduce price stickiness, a firm is assumed to adjust its price each period with probability 1－ω, as shown in the models of Calvo (1983) and Yun (1996).

The number of new credit matches in a period is given by a Cobb-Douglas matching function

where α∈(0, 1) and χ∈(0, 1) are constant parameters. A wholesale firm and a bank forming a credit match share the match surplus according to generalized Nash bargaining. Thus, is solved as

where b∈(0, 1) is the bargaining power for banks, f_t is the value of a productive wholesale firm, and g_t is the gain from a credit match for banks.

We log-linearize the structural equations around the efficient steadystate equilibrium as shown in the Appendix. For general stochastic nonefficient state, the Calvo-type stickiness introduced in the retail sector results into the standard Phillips curve with a cost-push shock ,

where δ is a positive parameter and is the inflation rate. The log-deviation of a variable (e.g., C_t) from its efficient steady-state value () is expressed as .

The retail price markup term in this equation can be obtained from the log-linearized version of Equation (29),

where ρ_u and δ₂ are positive parameters.

IS relation from equation (17) is given by

where we denote as the consumption gap.

Using the loan volume term , the credit market tightness term is expressed as

whereas the consumption gap is expressed as

Although the closed linear system is given by the five equations and the monetary policy rule is derived in the subsequent sections, we can also reveal the relation between the loan interest rate and credit volume as

Thus, the loan interest rate and the volume of credit have a close relationship.

Using linear-quadratic (LQ) approach of Woodford (2003) and Benigno and Woodford (2012), Fujimoto et al. (2014) show that a second-order approximation of social welfare includes a term involving credit, in addition to terms of inflation and consumption under the model with financial market frictions. LQ approach can analytically reveal an object of the central bank, although the effects are ignored more than the second-order. Benigno and Woodford (2012) show that the approximation error of LQ approach is sufficiently small in a fairly broad range of model specification for small shocks.

In detail, the second-order expansion of a household’s utility function around the efficient steady state is given by

where .

Fujimoto et al. (2014) reveal that the optimal policy faces a trade-off among the inflation rate, consumption, and credit market tightness. The presence of credit market tightness in the approximated welfare function has a novel implication for the optimal policy. Under credit market frictions, the optimal policy should respond to the inefficient state of the credit market, although the real economy is perfectly stable with no inflation and consumption at the efficient steady state level.

Fujimoto et al. (2014) also show a different form of approximated welfare as

Thus, the optimal policy, including macroprudential policy, requires stabilization for volume of credit. When ρ_u approaches zero, central banks need to stabilize credit variation to improve welfare.1 By contrast, when ρ_u approaches one, central banks need to stabilize growth of credit.2

1As the separation rate ρ approaches one, ρu approaches zero.  2As the separation rate ρ approaches zero, ρu approaches one.

Woodford (2003) shows that under the model with frictions in the goods market, that is, price stickiness, central banks should stabilize inflation and the consumption gaps, which roughly imply λ_θ＝0. He justifies that the simple monetary policy rules need to include these terms to improve welfare. Thus, the policy interest rate is explained by inflation and the consumption gap in the Taylor rule.

By contrast, Fujimoto et al. (2014) show that under the model with financial market frictions, a second-order approximation of the social welfare includes a term involving credit, in addition to terms of inflation and consumption. This outcome implies that the simple monetary policy rules need to include a credit term in addition to terms of inflation and consumption. Thus, we suppose that the Taylor rule needs some adjustments in credit variables such as credit volume and the loan interest rate.

In reality, some central banks pay attention to financial variables to implement the monetary policy under situations in which frictions in the financial market matter. For example, Taylor (2008) points out that a spread-adjusted Taylor rule that also includes the credit spread term in the standard Taylor rule can explain the easing of monetary policy by FRB in response to subprime mortgage crisis.

Therefore, we investigate whether adjusted Taylor rules achieve higher welfare than the Taylor rule does in the model with credit market frictions.

The model period is one quarter. We use the structural parameters in Table 1 for the Korean economy. Following Choi and Hur (2014), we set the relative risk aversion σ to 0.45, the elasticity of substitution between differentiated goods to 0.86, and the probability of price adjustment 1－ω to 0.14.

For other parameters, we assume β＝0.995 to set the steady state deposit rate to 2% per annum. We assume symmetric bargaining power (b＝0.5) following Den Haan, Ramey, and Watson (2003), and resort to the Hosios (1990) condition to set α＝b＝0.5.

We set ρ＝0.025 such that the average duration of a credit match is 10 years. We then normalize Z and L^* to 1, and choose κ, χ, and a such that the average duration of search in the credit market is one year for both wholesale firms and banks in the efficient steady state, and the annual loan rate is equal to 2.8%, which is the average real rate of all commercial and industrial loans by commercial banks in South Korea from 2001 to 2013.

In simulation, we assume a positive 1% cost-push shock in the Phillips curve with persistence of 0.5.

We check the performance of a variety of simple rules, namely, an estimated Taylor rule (TR), an estimated Taylor rule with a credit volume term (TRC), and an estimated Taylor rule with a loan interest rate term (TRL). TRC and TRL are given by

where ρ_i, ρ_c, ρ_π, ρ_l, and ρ_r are parameters. The introduction of credit volume and loan rate terms can be justified from Equations (10) and (8). As for TR, we use the parameters from Choi and Hur (2014), and set ρ_i＝0.81, ρ_c＝0.13, ρ_π＝0.5, and ρ_l＝0 in Equation (11).

In numerical simulations, we search for ρ_l and ρ_r to maximize the social welfare. The range of the policy parameters examined here is －5≤ρ_l≤5 and －5≤ρ_r≤5. Table 2 shows welfare for different rules. The welfare measure, evaluated by steady-state consumption, is given by the ratio ξ of a loss of alternative rule to that of the optimal monetary policy, as shown in Ravenna and Walsh (2011).

where L^opt is the welfare loss under the optimal monetary policy given by the first term on the right-hand side (RHS) of Equation (9) and L^spr is the welfare loss under alternative simple policy rules. As ξ becomes larger, the alternative simple rule results in larger welfare loss in terms of steady-state consumption.

The findings in the simulations are as follows. First, TRC and TRL perform better than TR under appropriate choices of parameters. In our exercise, TRC (TRL) shows the best performance, with ξ＝0.038 (ξ＝0.033), when ρ_l (ρ_r) is 0.1 (0.6) as shown in the first (second) row, whereas ξ＝0.067 for TR. These results are consistent with the theoretical investigation in the previous sections. In the Korean economy, the monetary policy focuses on the condition that credit volume and loan interest rate can perform well. Second, the best parameters of ρ_l and ρ_r are both positive. By increasing the policy rate, the loan interest rate increases. Thus, the future volume of credit decreases, which eliminates inefficient credit boom and achieving welfare improvement. Third, TRL shows better performance than TRC. Thus, for the Korean economy, adjustment in the loan interest rate on TR improves welfare more than that by credit volume. Fourth, TRC and TRL perform worse than TR when the parameters are not set appropriately, as shown in the third (forth) row. TRC (TRL) shows the worst performance as ξ＝0.44 (ξ＝1.6) when ρ_l (ρ_r) is 0.3 (2.4).

Inflation variability, consumption variability, and credit variables in the best TRC and TRL reported above have relative importance. The values of ρ_c＝0.13 and ρ_π＝0.5, are obtained from Choi and Hur (2014). which implies that the central bank respondsmore strongly to inflation than to consumption (or equivalently, output). In the case of TRC, ρ_l＝0.1 maximizes welfare, which indicates that the central bank should respond as strongly to credit volume as to consumption. As for TRL, the best value of ρ_r is 0.6, requiring a stronger response to the loan interest rate than to inflation.

We also check the performance of the simple macroprudential policy rule combined with TR. Here, we assume that the macroprudential authority aims to stabilize only the loan volume, such that the credit variation is the unique explanatory variable. This situation follows the conventional view of macroprudential policy. For example, the new Basel regulation imposes capital requirement on banks to primarily control the loan volume as in BCBS (2010, 2014). Moreover, Drehmann, Borio, and Tsatsaronis (2012) show that the variation of credit can be a good indicator to implement a macroprudential policy. We also consider the case in which the credit variation is replaced by the loan interest rate. More precisely, we assume that the macroprudential authority controls the bank’s bargaining power b_t in the Nash bargaining problem in response to the variation in credit or loan interest rate. In reality, the macroprudential authority controls the degree of banks’ competition in the credit market by changing the financial regulations. In this case, the markup Equation (4) changes to

The simple macroprudential policy rules are given by

We call these simple macroprudential rules as the macroprudential rule with credit variation (MRC) and the macroprudential rule with loan rate variation (MRL). By contrast, the central bank is only responsible for the stability of inflation and the consumption gap. Thus, we assume TR for the monetary policy.

The range of the policy parameters examined is －40≤ρ_l≤40 and －40≤ρ_r≤40. The result is reported in Table 2. MRC (MRL) performs better than TR, with ξ＝0.022 (ξ＝0.047) when ρ_l＝40 (ρ_r＝40), as shown in the fifth (sixth) row. Thus, the joint management of the macroprudential policy and monetary policy can achieve higher welfare than monetary policy alone. Moreover, MRC shows better performance than MRL. This result is different from that of simple monetary policy rule with credit terms.

However, under inappropriate parameters, MRC (MRL) performs worse than TR, with ξ＝0.09 (ξ＝0.071) when ρ_l＝－10.6 (ρ_r＝－11.4), as shown in the seventh (eighth) row.

For sensitivity analysis, we change the average duration of a credit match to five years. Thus, we set ρ＝0.05.3 Table 3 shows welfare for different rules.

First, welfare improves and deteriorates with TRC, TRL, MRC, and MRL in some cases. Thus, parameter settings are important to achieve welfare improvements. Second, TRL shows better performance than TRC. Third, MRC performs better than MRL. These results have some robustness.

We now expand the range of search for optimal parameters because the optimal parameters for MRC and MRL are at the upper bound of the range. The range of the policy parameters examined has expanded to －100≤ρ_l≤100 and －100≤ρ_r≤100. The result is reported in Table 4. MRC (MRL) shows better performance than TR, with ξ＝－0.015 (ξ＝0.0092) when ρ_l＝100 (ρ_r＝100). Other cases from Table 3 do not change.

Interestingly, MRC with ρ_l＝100, welfare is higher than in the optimal monetary policy because we assume the cost-push shock and macroprudential policy is set in the markup equation. Thus, the simple macroprudential policy rule can provide a large gain apart from the monetary policy, although such an outcome is sensitive to the shock and the macroprudential measure.

3In this case, a is 0.9918 and κ is 0.0059 with other parameters unchanged.

We show that the simple macroprudential and monetary policy rules with credit terms can induce higher welfare than the estimated Taylor rule under the parameters calibrated for the Korean economy. Thus, an introduction of simple macroprudential policy in addition to the monetary policy can improve welfare in the Korean economy.

The following points could be of interest for future research. By extending the model into an open economy, utilizing optimal capital control as the optimal macroprudential policy becomes possible. In this case, it would be interesting to investigate the dynamics of exchange rate under capital control.