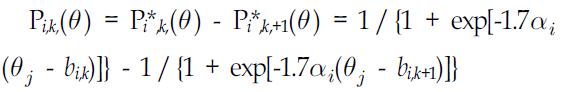진지한 여가의 특성을 이해하기 위한 가장 근본적인 문제는 신뢰 있는 측정을 실행하는 것이다. 여가학 분야에서 진지한 여가 측정 척도(SLIM)를 개발하기까지 전통적인 측정 이론을 바탕으로 한 문항의 신뢰성 있는 측정적인 속성을 증명하기 위하여 많은 노력들이 이어져 왔다. 이러한 전통적 측정 이론은 진지한 여가의 특성에 대한 정확하지 못한 의미를 도출할가능성을 지니고 있다. 따라서
Serious leisure activities are strongly interwined with attitudinal, economic, social, and psychological constructs. Thus, the measurement of serious leisure in leisure studies can be a very complicated and difficult issue (Stebbins, 1982, 1992, 2001a). Correspondingly, this leads to a concomitant effort to develop accurate and reliable measurement of serious leisure which forms the foundation of serious leisure research.
Since the term serious leisure was coined (Stebbins, 1982, 1992, 2001a), the attitude of serious leisure in leisure studies has been increasingly studied in a variety of contexts such as masters swimming (Hastings, Kurth, Schloder, & Cyr, 1995), bass fishing (Yoder, 1997), adult amateur ice skating (McQuarrie & Jackson, 1996), dog sports (Baldwin & Norris, 1999), motorsport events (Harrington, Cuskelly, & Auld, 2000), football fandom (Jones, 2000), computer gaming (Bryce & Rutter, 2003), college football fandom (Gibson, Willming, & Holdnak, 2002), adventure tours (Kane & Zink, 2004), sport tourism (Green & Jones, 2005), and quilting (Stalp, 2006). Furthermore, the recent short and long versions of the Serious Leisure Inventory and Measure (SLIM) provide an individual's attitude toward serious leisure on 18 subdimensions (Gould, Moore, McGuire, & Stebbins, 2008). The 18 subdimensions of SLIM consist of 72 items (4 items for each of the 18 dimensions) and 54 items (3 items for each of the 18 dimensions) for the long and short versions of SLIM respectively.
Despite the rich volumes of research in leisure studies, psychometric properties of items on SLIM have never been studied thoroughly. One major limitation of previous research in leisure studies is that researchers draw inferences based on classical psychometric techniques (e.g., using total scores and mean) without considering measurement theory. The classical psychometric techniques based on total score depend on the number of items and characteristics of samples under study (Hambleton, Swaminathan, & Rogers, 1991). Furthermore, it is essential to investigate the quality of psychometric properties of items on two different currently available types of SLIM since simple modification of measures has a huge impact on measures (Keller & Dansereau, 2001). In order to understand the importance of psychometric properties of items measuring the attitude of serious leisure, this study introduces item response theory (IRT) and demonstrates some of the IRT aspects that can be usefully applied in constructing measure in serious leisure.
Item response theory (IRT) has been widely used for analyzing psychometric characteristics of items and for estimating an individual's latent ability,
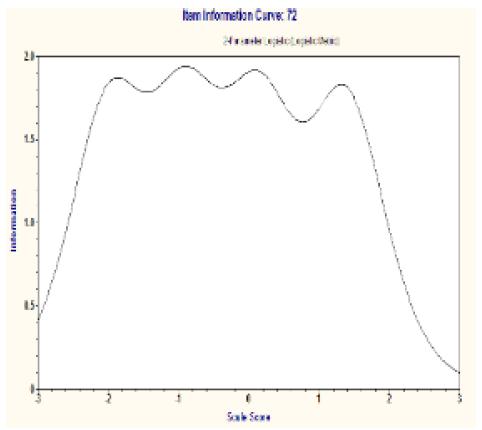
IRT provides a test information function and the standard error of measurement (SEM) to index the degree of measurement precision across the full range of latent abilities. Thus, SLIM can be evaluated in terms of the amount of information and precision it provides at specific ranges of latent abilities by using IRT. Item information for each item on a measure can be computed at any level of latent ability. Figure 1 shows that item 72 provides the most informative information across
Along with a test information function and SEM, it is helpful to reveal the relationship between item properties (e.g., item difficulty and item discrimination) and an individual's
It is also important to choose a proper IRT model for a measure in order to obtain accurate estimates of items and an individual's
2. Advantages of IRT over Classical Test Theory
The IRT approach for examining psychometric properties of items on a measure is much more complex than the classical test theory approach (CTT). However, IRT has a number of advantages over CTT to measure an individual's attitude toward serious leisure. Dependence between items and samples emerges as a major limitation of CTT in spite of the fact that the relatively weak theoretical assumptions (Hambleton & Jones, 1993) make CTT popular in various contexts such as coefficient alpha (Cronbach, 1951) and generalizability theory (Brennan, 2001). In the CTT approach, the commonly used item statistics in test development (e.g., item difficulty and item discrimination) depend on the particular characteristics of samples (Lord & Novick, 1968) and estimates of an individual's
IRT also provides more rich information than CTT does in terms of item-level information and SEM. CTT provides no item-level information about how an individual performs when confronted with items on a test. CTT yields a single estimate of reliability and provides corresponding standard errors of measurement assumed the same for all individuals (Hambleton & Swaminathan, 1985). Unlike CTT, IRT provides the item-level information function which indicates how well the item is working for each level of an individual's
In spite of all the potential benefits, IRT must be applied with great care in serious leisure research. Unlike CTT, IRT makes a number of strong assumptions such as unidimensionality and local independence. The inferences from the application of IRT are only valid when the underlying assumptions are met. The assumption of local independence is that a response to any one item is unrelated to the responses to other items once controlling an individual's
One practical limitation is that IRT models in general require relatively large sample sizes to obtain robust and meaningful results (Hulin, Lissak, & Drasgow, 1982). There is no absolute guideline about minimum sample sizes required for particular IRT models. However, regarding the issue of sample sizes in Samejima's graded response model (GRM), the simulation study (Lautenschlager, Meade, & Kim, 2006) showed that parameters of items and latent ability with 20 items and sample sizes of 200 on a measure had high correlation (.90) between generated and estimated parameters.
Construction and validation of psychological instruments involve analysis of the items by either traditional statistical methods based on CTT or IRT. Despite the advantages offered by IRT over traditional statistical methods of assessing performances, IRT has never been used in the leisure research field. This study aims at applying GRM (Samejima, 1969) to measure the recently developed SLIM. The MULTILOG (Thissen, 2003) computer program was used to estimate item properties such as item parameters and test information functions for 72 items. Next, the least desirable items identified on the basis of their item information function were removed from the scale.
Leisure activity participants who have memberships with fitness centers in Seoul, Korea, were asked to complete the questionnaire consisting of 72 items to measure serious leisure. A cluster random sampling method was utilized (50 participants from each of the randomly selected six fitness centers). Specifically, all fitness centers in Seoul were alphabetically numbered and six centers were selected using the table of random numbers. Paper-and-pencil surveys were distributed to 300 leisure activity participants and returned directly to the survey administrators. Of the 300 questionnaires that were collected, 45 of the surveys were not included in the analyses because they had data missing not at random with 50% or more on two or more scales. Finally, a total of 255 surveys were utilized for the analyses of this study. The average age of the participants was 29.06 years (SD=9.65) and all respondents were 18 years old or older. Of the 255 participants, the majority were male (61.2%). The average annual household income was $42,310 (SD=32,660), and 66.7% of the respondents were married.
SLIM, developed by Gould et al. (2008), was translated into Korean. The questionnaire for this study included SLIM, consisting of 72 items, and demographic characteristics. The short and long versions of SLIM assess 18 subdimensions. All items were measured with a Likert-type scale (1 – strongly disagree to 5- strongly agree).
Samejima's GRM was implemented in the MULTILOG (Thissen, 2003) computer program since item responses are ordered categorical responses. GRM can be considered as an extension of the two-parameter model for polytomous items and computes conditional probability for successive steps and estimates each response category’s probability of proficiency at each possible value of an individual's
GRM determines boundaries reflecting where a given individual is expected to obtain a certain category score (or higher) versus those categories below. GRM computes threshold parameters,
Pi,k,(
For the lowest and highest options, the lowest assumes the probability is 1.0 that the response is in or above the lowest category, whereas the highest assumes the probability is zero that the response is above the highest category.
The dimensionality of SLIM was tested by principal axis factor analysis with the varimax rotation method in order to check unidimensionality. The results indicated that eigenvalues of the first factor were about eight times superior to the second factor, and the first factor also explained 43.9 % of the total variance. Comparison of the ratio of the 1st to 2nd eigenvalues to the ratio of 2nd to 3rd eigenvlaues resulted in the value of 7.272 and provided an additional evidence for unidimensionality. Thus, it is reasonable to conclude SLIM sufficiently satisfies the assumption of unidimensionality, althougth the SLIM was originally designed to measure more than one factors.
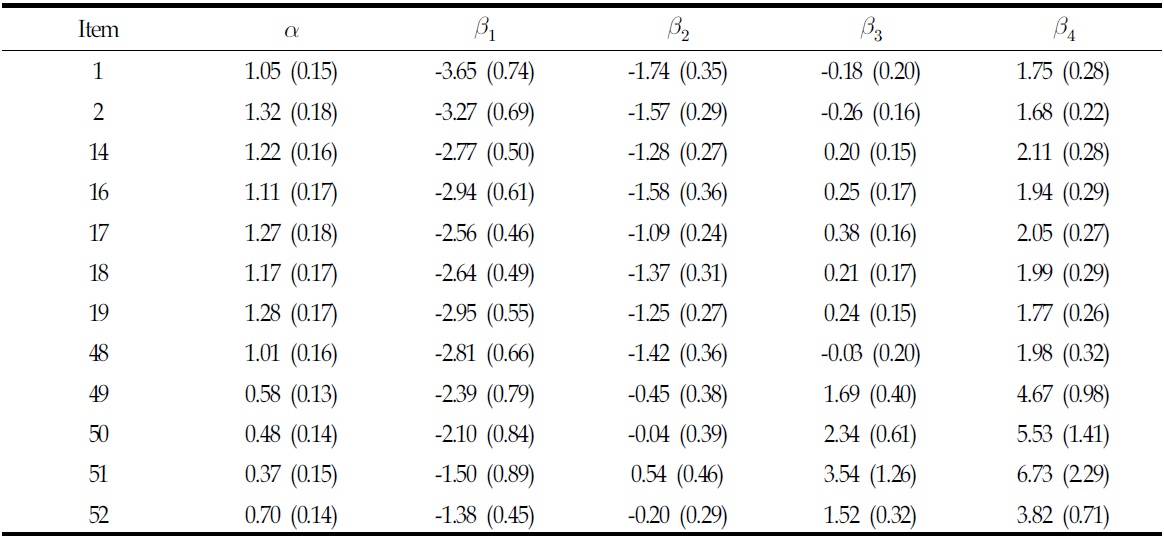
The marginal reliability of SLIM was .9828 for the 72 items, and biserial correlation ranged from .297 to .750. Marginal reliability dropped slightly less than .004, from .9828 to .9824 once deleting 12 items which were identified as poorly constructed ones in terms of item information function as shown in Table 1.
[Table 1] Item parameters for the deleted 12 items
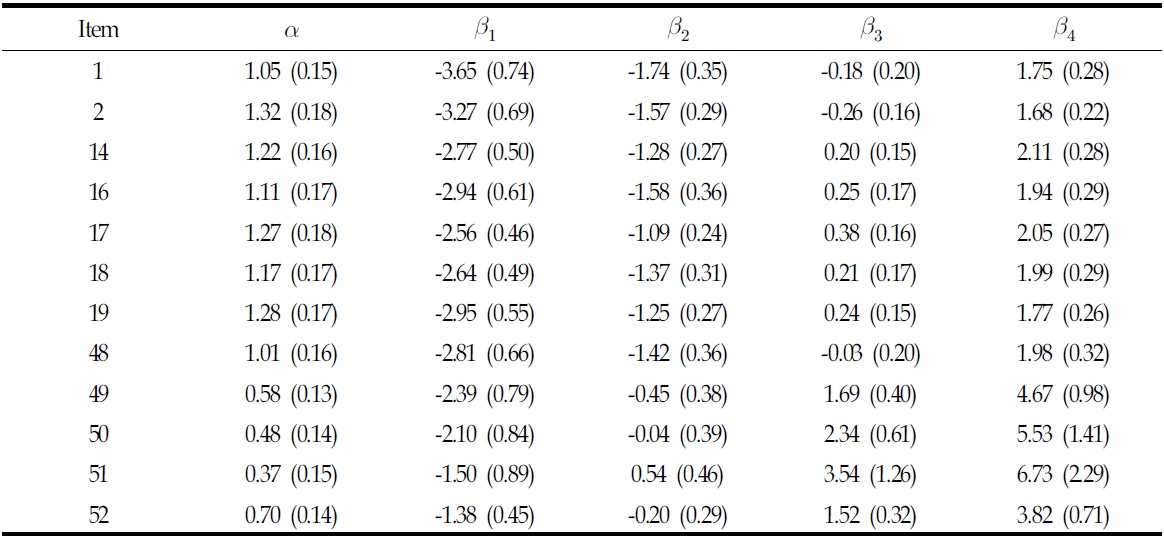
Item parameters for the deleted 12 items
Difficulty parameters across 72 items were mostly negative values. This indicated that serious attitudes were not required to respond to items on SLIM because lower scores reflected a less serious attidude. These results might imply that SLIM seems to be more appropriate to measure individuals who lie on the middle range of serious leisure.
Once the 72 items were analyzed by GRM, item and test information functions were calculated. The amount of item information at different levels of an individual's
However, some items (1, 2, 14, 16, 17, 18, 19, 48, 49, 50, 51, and 52) provided relatively little information compared to other items.
The item information functions of those 12 items were relatively flat across the whole range of an individual’s
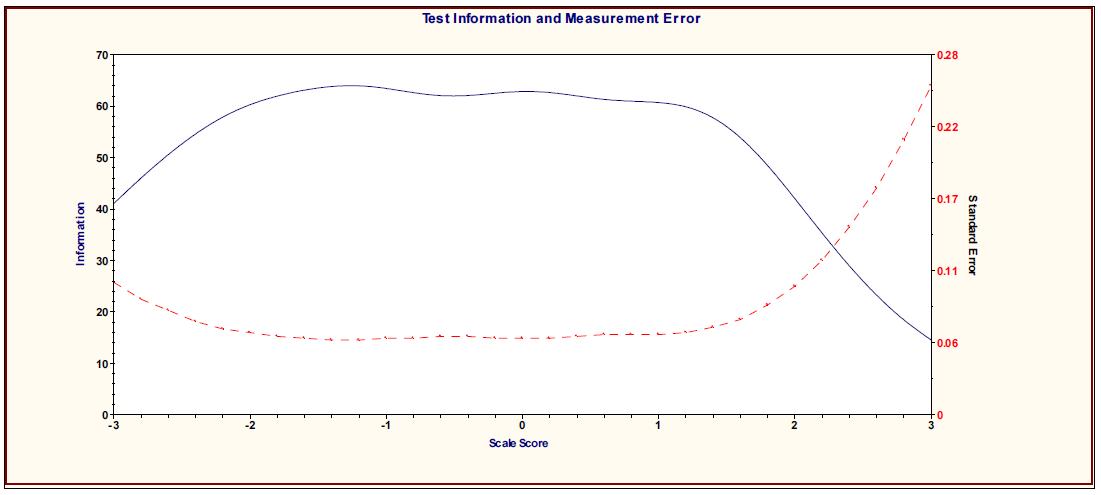
In addition, item information functions for each of the 72 items were aggregated to form the test information function which showed how precisely
SLIM measures the individual’s
The aim of this study is to assess and evaluate the precision and accuracy of SLIM in order to determine how useful SLIM is for research, self-evaluation, and self-improvement. Item response theory (IRT), especially Samejima's (1969) GRM, is used to achieve this end.
SLIM can provide strong measurement precision across most of the range of serious leisure latent traits. Item information functions for each of the 72 items revealed that SLIM performed well for individuals with low to moderate levels of serious leisure attitude. The test information function for the 72 items on SLIM was relatively high and flat.
However, measurement precision tended to decline somewhat at the extreme ends of the latent traits and became increasingly unreliable in assessing individuals with high levels of serious leisure proficiency, which means that SLIM is not an appropriate instrument for selecting individuals having high serious leisure proficiency. Instead, SLIM is more applicable for identifying individuals lying between the low and medium high serious leisure attitude levels on the continuum.
Furthermore, this study reveals that more accurate responses could be obtained while taking less time to collect data because SLIM could be shortened without a noticeable drop in its measurement precision and marginal reliability.
Items with low discrimination power, especially those that have low item information, do not contribute much to the test information function and those items could be safely removed from SLIM. Hence, researchers can save time and cost to collect data with reliable items and can obtain better estimate respondents' attitude given the respondents' responses to items on SLIM with less measurement error. Furthermore, the findings from this study suggest SLIM might need more difficult, highly discriminating items for individuals having serious leisure attitude.
Despite the advantages offered by the IRT over the traditional statistical methods based on the classical test theory, IRT is rarely used in the serious leisure research field due to various difficulties (Hambleton & Jones, 1993; Magno, 2009). First of all, most researchers who have used classical test theory (ANOVA and factor analysis) need to become familiar with and understand the terminology used in educational testing because IRT has been developed within the educational and psychological testing framework. In addition, it is difficult for researchers to understand the mathematical complexity used in IRT and to select appropriate IRT models among various IRT models. The most difficult obstacle to applying IRT in leisure research is IRT computer programs, which are not user-friendly. Despite these limitations, practical applications of IRT in the field of serious leisure cannot be ignored because only an accurate instrument can enhance the understanding of seriousness in leisure.
The current study examined the psychometric properties of items and individuals. The results shows that SLIM without items having low item information has a higher degree of internal consistency than SLIM using all 72 items. The most important implication of using IRT is that an optimal number of items can be obtained while increasing reliability and validity. In addition, several interesting extensions are straightforward within the previously mentioned GRM. The more important ones are models with more item parameters (e.g., adding pseudo-guessing parameter) and models with covariates.
Although these finding support the usefulness of SLIM for measuring seriousness of leisure, it is necessary to investigate measurement invariance across cultures because the concept of serious leisure might be different across different cultures.