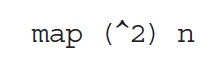There has always been a lot to like about Chalmers’ article. You might have thought, for example, that a theory of implementation should be most concerned with telling us which things compute at all. Chalmers argues―convincingly, in my opinion―that this is less interesting than the question of which computations things p erform. On his account, everything computes something or other. But only complicated things instantiate complicated programs. Computationalists about mind and brain arguably don’t need much more than that. Whatever computation our brain performs, it’s surely a doozy. Relatively few things manage it.

Put another way, a theory of implementation also implies a categorization of computing mechanisms. Chalmers’ condition CSA nontrivially partitions the world into objects that perform the same computation.1 That’s useful when we go to investigate, predict, and explain the behavior of computing machines: things that perform the same computation ought to do the same things, have the same parts, and be approached in the same way.

Many balk at the liberality of Chalmers’ account. I don’t. I have a different worry. CSA doesn’t just divide the simple computations from the complex ones. It also makes distinctions among the complex computations. In particular, it seems to imply the following taxonomic principle: two objects perform the same computation if and only if they perform the same steps in the same order. That falls out of CSA more or less directly. Computations are specified by specifying state-transition rules. These prescribe, in precise detail, the transitions that an implementing machine must undergo for any particular combination of substates.2 So it follows that two implementations of the same computation on identical input will undergo the same statetransitions in the same order.

That used to seem obvious to me. Now it doesn’t. In what follows, I’ll try to explain why.

Thinking about the implementations we make can help us get a handle on the one we don’t. So first, consider machines that are explicitly programmed to do something. Computer scientists distinguish between two types of programming styles: the imperative and the declarative.3 Most well-known computing languages are imperative languages. As Hudak puts it:

Imperative languages specify a sequence of commands to be followed. The commands themselves alter and change the state of variables, which can in turn affect which commands will be followed at a future time. This should sound familiar even to non-programmers: it is just the picture of computation embodied in CSA.

Declarative languages treat programs differently. I’ll focus on functional programming languages, a subset of the declarative ones.4 The primary construct in functional languages is, unsurprisingly, the function. Writing a program thus consists of writing a set of functions, and running a program consists of evaluating a function for some values. A program thus describes which functions are to be computed, but neither constrains nor guarantees the order in which functions are evaluated. This is possible because functions can only return new values, not change the value of existing parameters. Pure functional languages are thus side-effect free: calling the same function with the same parameters will always return the same value.

An example will clarify the difference. Suppose we had a list n of integers, and wanted to determine the square of each. In imperative languages, this is most naturally modeled by looping over the list and squaring each member in turn, illustrated by the following pseudocode:

Note that the program implicitly specifies the order in which the members of n are to be altered: from first to last. We could also make a program that runs in the opposite direction. CSA tells us, however, that this would would be a different program. Note too that the values of n and t change in the course of running the program. That’s part of the reason why explicit ordering matters: since computations can have side-effects on variables, one must ensure that the right computations are performed at the right time. The side-effects don’t happen to matter much in this case, but the presence of mutable data structures requires explicit ordering of steps.

In a functional language like Haskell, the same computation can be done quite differently:

The map function takes a partial function and applies it to each member of a list. The order in which it does so is not specified. Rightly so, for the order is irrelevant: list n is not altered in the process (instead, a new list is returned), and the result of squaring one element does not depend on the square of any other element. As such, functions like map can be done in parallel: a clever implementation could farm out the computation for each element to any number of distinct processors.5 But that means that the order in which substates of a implementing system transition is underdetermined by expressions like the above: the same computation could be done in a different order by different machines. So there seems to be a way of specifying computations without specifying the order in which substates must change. Constructs like map, then, specify what should be done, not the order in which it must be done.

A few remarks are in order. First, as functional programs specify functions to be performed without specifying order of execution, one might think that they reside on a different plane. In particular, one might think that they belong to Marr’s computational level rather than the algorithmic one [Marr, 1882]. I don’t think this is the place for Marr exegesis, but I do think that the similarity is only superficial; as Hudak notes, the difference here is one more of degree than kind ([Hudak, 1989] 361). For one, functional languages exist. You can write programs in them and they will run. That alone should distinguish them from the abstract computational level. Further, functional programming is not magic: calculating any moderately complex function requires breaking it down into coordinated application of the primitive functions of the language. The resulting algorithms can be evaluated for their computational complexity, their minimum time and space requirements, and so on. In short, they have the same kinds of properties as familiar imperative algorithms. None of these properties apply to descriptions at Marr’s computational level. Finally, it is not obvious to me that functional programs are strictly more abstract than their imperative counterparts; functional programs; rather, they abstract away from different things. I will return to this point in detail below.

Second, any non-trivial implementation will, when running, change its state in some way or other. This is true even in implementations of functional languages. The point is just that implementations of the same program need not change state in the same order to count as the same program. Third, some of these state-changes must come before others. In the Haskell expression (add x (div y z)), for example, the inner div function must be computed before its value can be added to x.6 Order of evaluation is specified by the logic of the functions involved, though, not by the program.

Fourth and finally, it is of course true that any particular concrete computation of the above function could be described as a series of steps executed in a particular order. But that is irrelevant. Any particular concrete computation could also be described in minute detail as a series of atoms going to and fro. Imperative descriptions of computations abstract away from the fiddly details of material composition. That’s a good thing, and few complain. I argue only that this very same abstraction process can be taken even further. We can also describe computations in a way that does not specify the precise order of steps involved. So I’m not making the absurd claim that physical implementation doesn’t happen in time, or that we couldn’t describe the temporal ordering of facts; again, the claim is only that two implementations of the very same program can change state in different ways at different times. To put it in Chalmers’ terms, what is “organizationally invariant’’ across implementations need not be the temporal order in which steps are performed.

1Strictly speaking it’s the conjunction of FSA and CSA that does the work. Since most interesting machines are going to fall under the scope of CSA, I’ll focus on that.  2I ignore for the sake of space the case of probabilistic state-transition rules.  3For a good introduction to the difference, see [Hudak, 1989]. Backus gives a more polemical account in his [Backus, 1978], reflection upon which which has greatly influenced this paper.  4The most well-known language with functional characteristics is Lisp, though Lisp is technically multi-paradigm and includes declarative features. Haskell, Miranda, and Erlang are probably the best-known purely functional languages.  5This is not just a theoretical possibility; Google makes heavy use of a parallelized version of map to deal with large datasets. See [Dean and Ghemawat, 2008] for technical details. Chapter 22 of [Spolsky, 2008] is both a more accessible introduction and a partial inspiration for this section.  6Though note that the order need not be what you might expect. Haskell functions are curried, so an expression like Add 2 3 returns a partial function x + 2 which can be applied to the second parameter.

The points above are suggestive, but they are limited to programs rather than their implementation. I believe they can be generalized, however, to a point about implementation as well. There are, I suggest, two ways to understand implementation. Call them the Turing Paradigm and the Church Paradigm.

Consider a simple Turing machine—call him Art—who performs a parity calculation. Given an input string of n strokes, he’ll loop over it, merrily deleting the strokes, and end by writing a stroke if the initial input was even.

There are at least two ways in which we might understand Art’s behavior. First, we might note that Art’s behavior is isomorphic to Table 1. (Assume that Art satisfies the conditions set forth in CSA, plus whatever other counterexample-barring conditions you please.) Knowing Art’s machine table lets us predict and explain his behavior.

Thinking of implementation in terms of machine tables—or, more generally, in terms of abstract specifications of state-transition rules—also commits us to categorizing Art in certain ways. CSA embodies both of these commitments. First, Art’s machine table specifies a series of steps and the conditions under which they are to be followed. So any other machine which performs this computation will do the same things as Art does, and in the same order. Second, Art has a number of parts: a read head, a tape, and something to keep track of state and transition in the right ways. Any machine that computes as Art does will thus have computationally similar parts. Of course, those parts may made of different stuff, they may be faster or slower, efficient or wasteful; computation is meritocratic that way. Whatever implements the same computation, however, will have a set of parts that are similar to Art’s.

Call these commitments together the Turing Paradigm of computation. The Turing Paradigm suggests a story about how we ought to investigate and understand computing systems. Take something that performs an unknown computation—say, the brain. The primary task of understanding a new computation is twofold. First, figure out which parts correspond to inputs, state, and data. Second, figure out the steps and ordering principles that cause the relevant transitions between states. Do this, and you’ll understand the computation that the brain performs.

We can also describe Art’s behavior in a different way. To begin, consider the pair of functions in figure 1::

Suppose you wanted to solve for some particular value of f₁ – f₁([1, 1, 1, 0], 1), say. You could do that in lots of ways (pure intuition; trial and error; paying for the answer). But one possibility—and one that’s guaranteed to work if the function is well-defined—is to solve by successive functional substitution. Since the first element of the list is 1, the value of the function is given by f₂(r([1, 1, 1, 0], 1, 0), 1′). Substituting again, the value will be is f₂([0, 1, 1, 0], 2). Do this over and over again, and you’ll get the answer.

This is, of course, precisely what Art does. Start him on a list s of strokes and he computes f₁(s, 1). He does so by serial substitution of functions: the read head performs the primitive function index, the write head does replace, and so on. Having appropriately substituted, he then tries to compute f₂ on the new input with n = 1′. And so on and on until he halts, the now-altered tape giving the value of f₁(s, 1).

So, here is an alternative—admittedly loose and informal—model of implementation. We may specify a computation by specifying a set of functions. These divide into primitive functions and recursively defined derived functions. Something implements this computation if it has a mechanism for calculating the primitive functions, a mechanism or mechanisms that coordinate functional substitution, and when run actually does functional substitution in an appropriate way. Call it the Church Paradigm of computation, inspired by the process of normal form reduction in the Lambda Calculus.

Adopting the Church paradigm makes clear why a specification of an implementation need not specify the order in which steps are taken. Functional substitution itself demands that the value of functions be determined before others.8 Further, in many cases the process of functional substitution can be done in many different orders without affecting the result. So which substitutions are done when can be left up to the implementation of the language.

7I’ve used lists to make the parallel obvious. If you’d prefer a more mathematical flavor of functions, you could replace everything with, say, Gödel-encoded integers. I see no formal reason to prefer one over the other, though more specific explanatory interests may give us a reason.  8Though the optimal order of evaluation is itself a complex problem; see [Hudak, 1889] §2.2.

If we cared only about adjudicating which things compute, then there would be no difference between the Turing and Church paradigms. (Save, of course, that Chalmers has done a very nice job of formalizing implementation on the Turing paradigm while I’ve at best waved my hands at the Church version.)9 But Chalmers has shown that we should care about more than that: we should care about how we individuate implementations as well. So the difference matters in two ways.

First, if we care about taxonomizing implementations, then the Church paradigm will group together implementations that the Turing paradigm counts as distinct. The preceding pair of functions might, for example, be implemented by a distributed series of distinct mechanisms—one to calculate index, one to calculate replace, one to calculate the successor function, and another to make sure everything gets to the right place. The order in which these distinct mechanisms do their job might differ from the order in which Art performs them. On the Turing paradigm, different order means a different computation. On the Church paradigm, by contrast, we do not specify the order in which functions are evaluated; that’s left up to the details of implementation. So on the Church paradigm, our hypothetical machine should count as performing the same computation as Art.

An important clarification. I have said that the Church paradigm abstracts away from certain details that Turing accounts focus on. But that does not imply that the Church paradigm is strictly more abstract than the Turing one. In fact, I think it isn’t. Computations that the Church paradigm counts as distinct might be implemented by the very same Turing Machine. A simple example: the Haskell functions sum and fold (+) 0 both give the sum of a list of integers. The very same Turing Machine could implement both functions. Yet arguably, they count as distinct from a functional perspec-tive: the former is a one-place function, while the latter is a partially applied three-place function.

If this is right, the mapping from Church-similar computations to Turingsimilar ones is really many-many. The two ways of carving up computations cross-cut each other, rather than one being more abstract than the other. And that is what we should expect given their differing focus. The Church paradigm groups computations based on the mathematical functions they implement, abstracting away from temporal ordering of steps. The Turing paradigm groups computations based on temporal ordering of primitive operations, abstracting away from the mathematical functions performed. The two thus carve up the space of computations differently.

Second, if we care about explaining implementations, then the two para\-digms will tell us to look for very different things. The world of the Turing paradigm is one of states and their transitions. The Church paradigm, on the other hand, tells us to look for function-applications and their coordination. What we understand as the mechanistic parts of an implementation, and how they work together, will differ on each paradigm. That matters. Mechanistic strategies are important for understanding complex biological systems like brains, and such strategies rely crucially on a decomposition of a system into appropriate parts [Craver, 2007]. The difference between the two paradigms, therefore matters when we look to explain how implementations work.

9Spelling out the Church version more fully would require cashing out two notions: function application and function coordination. I take it that both can receive a straightforward physical interpretation: function application consists of the transformation of some values into others, while function coordination consists of passing values to the appropriate bits that do functional application. Specifying that at the relevant level of abstraction beyond both the scope of this paper. Cashing out such notions in physical-functional terms seems like a reasonable possibility, however, and that makes the present at least a sketch of a theory of implementation, not just program specification. Thanks to the reviewers for pressing me to clarify this point.

How we understand a particular implementation will thus depend on how we conceptualize implementation itself. I don’t think that either paradigm is inherently superior; which we adopt should depend on our explanatory interests. Sometimes we really do want to know about the particular computational steps and the order in which they’re performed; sometimes knowing these details is just more illuminating. If so, we should understand implementation as Chalmers suggests. Other times, however, thinking of functional application and its coordination is more useful.

I’ll conclude with one place where I think the Church paradigm deserves more attention. What I care about most is brains. I’d like to know how they work. I think computationalism is a promising strategy for figuring that out. And I think that the Church paradigm might be a better way to understand which computations brains implement.

There is increasing evidence that individual brain regions are specifically involved in a multitude of distinct cognitive tasks (pluripotency), and that the same cognitive task can specifically activate distinct groups of brain regions, either simultaneously or at distinct times (degeneracy).10 One way to understand these facts is what Michael Anderson has termed the Neural Re-use Hypothesis (NRH) [Anderson, 2007, Anderson, 2010]. According to NRH, neural circuits originally used for one task can be re-used in different tasks. Importantly, this need involve no or only minimal change to the region itself. The same (type) of function is performed; what changes instead is the pattern of connectivity between the region and other functional regions. What matters for cognition is, then, not just what brain regions are doing, but how that activity is connected with other brain regions. The resulting picture of brain activity might be like that suggested by Luiz Pessoa for emotion [Pessoa, 2008], in which some regions perform specialized (but domain-general) computations, and their activity is flexibly coordinated by densely connected hub regions like the amygdala.

This picture of brain activity, I suggest, resembles the Church picture of implementation more than the Turing alternative. On it, what matters for understanding the brain is understanding the coordination between the computation of primitive functions. Conversely, if this is right then looking at state-changes won’t be terribly telling: as brain regions are pluripotent, changes in their state are interpretable only by looking at the total context of activation. Along the same lines, degeneracy implies that there is often more than one neural route to performing the same task, and that different routes might be chosen at different times depending on overall brain context. So looking at the particular sequence of steps performed during a task might obscure important similarities between spatially distinct patterns of brain activation.

Again, that is not to imply that the particular sequence of neural steps is unimportant tout court: temporal ordering is an critical part of what the brain does. Nor is it to imply that for some explanatory tasks, learning about that temporal ordering might be a crucial step for understanding what the brain is doing. Rather, it is just to suggest that for some explanatory purposes—and in particular, for understanding the interrelations between different brain areas—temporal ordering may be less important than identity of mathematical function. If that’s so, then the Church paradigm might let us make progress where a Turing model would get bogged down in details.

These models of brain function are still in their infancy. They might be wrong. But they seem worthy of consideration. If so, then we should at least consider models of implementation that would let us understand them. Should Turing’s way fail, we may have to take our brains back to Church.11

10For pluripotency and degeneracy, see for example [Price and Friston, 2002, Friston and Price, 2003, Price and Friston, 2005, Poldrack, 2006]. Carrie Figdor connects degeneracy to arguments about multiple realizability; importantly for my purposes, she notes that we can get flexible implementation of cognitive functions even within the very same system at different times [Figdor, 2010]. The point of the present paper, however, is broader than usual multiple realizability arguments; it is similar in scope to Putnam’s argument for multiple realizability even at the computational level ([Putnam, 1991] Ch 5).  11Thanks to Jim Virtel and three anonymous reviewers for extremely helpful comments on a previous draft.