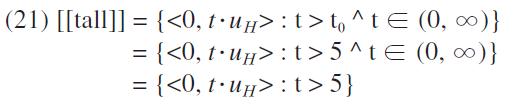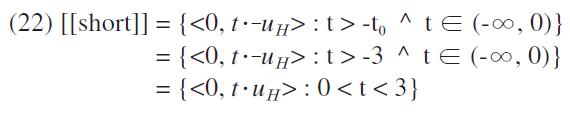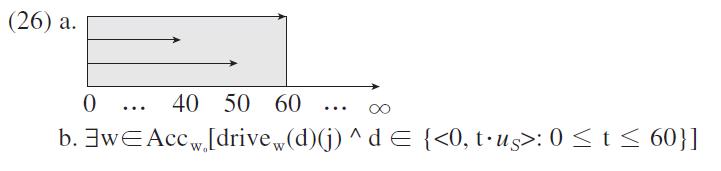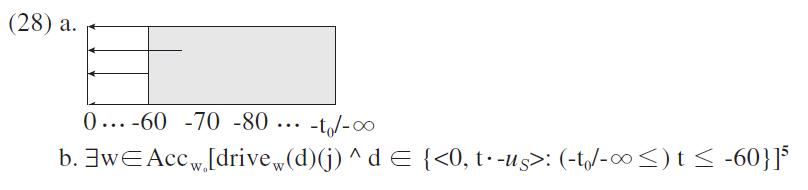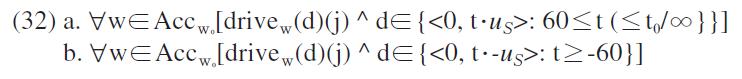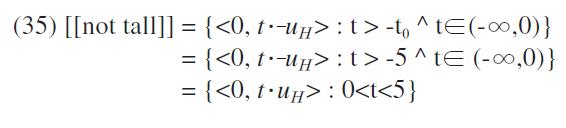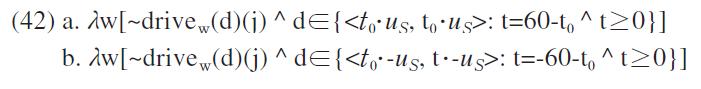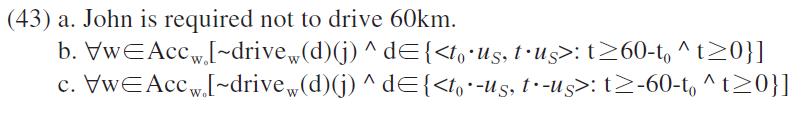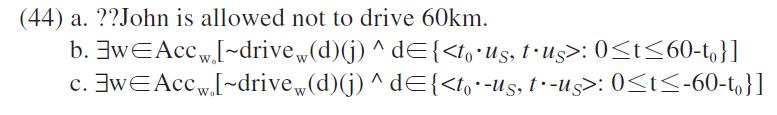Traditionally, an interpretation domain consists of individuals (and possibly materials), and nouns and predicates are understood to denote sets of individuals (or materials) in this domain. Depending on theories, additional entities of events or situations are required to construe verbal predicates. No matter how diverse entities an interpretation domain includes, all these entities are defined by inclusion. A larger set includes smaller sets, which reflects relative specificity of meanings between expressions.

Unlike nouns and predicates, the interpretations of number words cannot be done by the set inclusion of entities. The meaning of five cannot be defined by the inclusion of lower numbers such four or three. Moreover, numbers are in an ordering relation. Thus, an issue to deal with number interpretations is what entities are needed and how they are structured. Additionally, we need to probe into what numeral readings number words have. Basically, number words without any modification are interpreted in two ways: ‘exactly readings’ and ‘at-leas t readings.’ For example, the number three is construed either as ‘exactly three’ or ‘at least three,’ and the sentence in (1a) means either (1b) or (1c).

In the exactly reading, both the upper and lower bounds are specified by the number, so it is also called a ‘two-sided’ reading. In the at-least reading, only the lower bound is restricted by the number, which makes it called a ‘one-sided’ reading.

No matter which reading a number word takes, its interpretation is varied in a sentence with a modal operator. Allow and require are deontic modal operators that quantify over goal or ideal worlds. Allow is an existential quantifier on worlds while require has universal quantificational force on worlds. When a number occurs in a sentence with a modal operator, its exactly reading is not licensed.

In both (2a) and (2b), three is not interpreted as ‘exactly three.’ Three has contrasted readings in the sentences other than this common property. Three in (2a) is construed as upper-bounded and three in (2b) lowerbounded as paraphrased. Given the fact that (2a) and (2b) are minimally differentiated from (1a) with the insertion of the modal operators, the distinct readings of three in (2) are attributed to the interaction of the modal operators and the number word. Note that meaning interactions of number words are not confined to modal operators. When a negative operator occurs with a sentence without a number, it does not affect the acceptability of the sentence. However, occurring in a sentence with a modal operator and a number, the acceptability of the sentence may be different depending on the scope of negation.

To trace the interaction between number words and modal and negative operators, I will consider the interpretations of number words in semantic literature. Much theoretical and experimental evidence shows that numbers are uniformly interpreted as two-sided. Based on the exactly readings of numbers, I will critically review a previous analysis on number readings in sentences with operators, and propose an alternative analysis in the framework of Vector Space Semantics.

The semantics of cardinal number words has been considered as no different from other scalar quantifiers such as some and most. Just as some is lower-bounded and the cases for all are excluded by scalar implicature, the lexical meanings of number words areonly lower-bounded and their two-sided readings, i.e., exactly readings, are derived via the pragmatic inference of scalar implicature. (cf. Horn 1972 & 1989, Gazdar 1979, Barwise & Cooper 1981, Levinson 1983 & 2000) According to this Neo- Gricean view, a phrase like two cats does not mean exactly two cats but rather at least two cats. Thus, John has two cats is understood true in the situation that John has three, four, or a hundred cats.1

This dominant view on numbers has been challenged with theoretical and experimental evidence in the last decade. In contrast with the lowerbounded semantics of numbers, this alternative view takes the ‘Exact Semantics’ on numbers, where the lexical meanings of numbers include both upper and lower bounds. Koenig (1991) argues that if we follow the Neo-Gricean analysis, the semantic role of numeral modifiers is not systematic. Numeral modifiers that are lower-bounded or two-sided, e.g., at most or exactly, modify the content of numerals. However, numeral modifiers that are upper-bounded like at least play the role of implicature suspender. Intuitively, at most and at least are differentiated only by monotonicity. However, their semantic roles should be sharply distinct between semantic modification and pragmatic implicature suspender.

According to the Neo-Gricean analysis, numbers and scalar quantifiers are equally one-sidedand assigned exactly readings by scalar implicature. The exact interpretations of scalar quantifiers are explicitly represented by delimiting the upper bound. For example, the exact reading of some is glossed as some but not all. This delimiting implies that the lexical meaning of some includes the cases that all applies. In contrast, the exact meaning of a number word is represented by focusing the cardinality itself rather than delimiting the upper bound. For instance, the exact reading of two is glossed as exactly two rather than two but not more than three. This contrast suggests thatthe lexical meaning of a number word includes both the upper and lower bounds and that the exactly reading is not the result of scalar implicature.

If numbers are only lower-bounded as Neo-Gricean theorists’ claim, the explicit representation of lower limit should not affect the truth of sentences with a number. Lexically specified lower limits affect only the pragmatics of sentences. However, as Nouwen (2010) notes, the acceptability of a sentence may be worsened with the addition of a numeral modifier delimiting a lower (or upper) limit.2

In the Neo-Gricean analysis, the propositional content of (3a) is that John registered at least three classes, and the exactly reading of three classes is pragmatically derived with no implicature cancellation. Then, the semantic reading of (3a) equals to that of (3b), which predicts that the two sentences should not be distinct in their acceptability. However, this prediction is not borne out as shown by the different judgments of the sentences. This contrast clearly shows that three cannot be just lower bounded.

Another point made by Koenig (1991) is that the apparent scalar implicature of numbers is related with the distributivity of predicates. Implicature cancellation is allowed only for a number occurring with a distributive predicate but not for the one with a collective predicate.

Carry a box is ambiguous between distributive and collective. When the sentence is accompanied by the distributive quantifier each as in (4a), the predicate is solely construed as distributive. On the other hand, the occurrence of together forces the collective reading of the predicate. In (4a), the upper-bounded implicature of two is overtly cancelled by the second sentence, where the number of the carriersis specified as three. However, the same cancellation is not licensed in (4b). The awkwardness in (4b) shows that the exactly reading of two is not pragmatically driven.

The theoretical debate between the Neo-Gricean analysisand the Exact Semantics leads to a number of experimental study. (cf. Noveck 2001, Papafragou & Musolino 2003, Musolino 2004, Huang & Snedeker 2009, Geurts et al 2009) The experimental results of the study show that both children and adults take two-sided readings instead of lower-bounded ones. For example, Huang et al (2009) conducted an experiment to test whether number words have lower bound readings or exactly readings. The experiment is designed to provide contexts in which scalar implicatures are cancelled to disentangle semantic and pragmatic contributions to the meaning of number words. Since implicatures are not part of truthconditional content of sentences with a number word, they should be cancelled (or not calculated) in contexts in which none of given options are compatible with them. In the experiment, they provide three pictures, two with visible boxes and one with a covered box. One of the visible boxes contains one fish, and the other one has three fish.If the Neo-Gricean theory works with subjects’ interpretations of numbers, subjects are supposed to choose the box with three fish when asked ‘give me the  box with two fish.’ Since none of the visible boxes matches with the request, subjects should cancel the scalar implicature and pick out the boxwith a larger number of fish than two. On the other hand, the Exact Semantics predicts that subjects should choose the covered box because there is no match for the request. When there was no exact match, 95% of children and 100% of the adults chose the covered box in the experiment. The experimental result is inconsistent with the Neo-Gricean analysis, showing that number words haveexact semantics from the very early stage of acquisition.

Since the exactly readings of numbers gain more support with theoretical and experimental evidence, I will assume that numbers have both upper and lower limits in the following discussion.

As discussed in the previous section, much evidence shows that number words are two-sided and have exactly readings. Part of the evidence is provided by Nouwen (2010), which points out the fact that numbers may not be modified by expressions with an upper or lower limit.

As shown by the awkwardness in (5b) and (5c), the numeral modifiers at least and at most may not modify three because their assertion of lower or upper bound is against the semantic interpretation of the number. Interestingly, when the number occurs in the scope of a modal operator, it has a one-sided reading, and which side is bounded is determined by the monotonicity of the operator.

The sentences in (6a) and (6b) are distinguished from (5a) only by the insertion of the modal operators allow and require. The occurrence of the existential operator in (6a) induces the upper bound reading of three and that of the universal operator in (6b) the lower bound readingas paraphrased.

The semantic change of the number is not limited to allow and require. Other modal operators show the same bound readings. Here are more examples of modal operators which render numbers to be one-sided. (cf. Kennedy in progress)

These sentences have different contexts with different operators, but they have the same bound readings. The sentences with the existential operators all have at-most readings while those with the universal operators have at-least readings. The consistent division of the interpretations suggests that the different bound readings of the numbers are due to the different monotonicity of the modal operators. Then, here is a question to be answered: why does the insertion of the modal operators change the numeral readings of the sentences? No matter which strategy is taken to account for the meaning change, it should be based on the interaction of the semantics of modal operators and numbers.

What affects the interpretations of numbers is not confined to modal operators but includes negative operators. When sentences are not accompanied by number words as in (9), the modal operators in the sentences trigger quantification over worlds.

The existential modal operator in (9a) induces the reading that there is a world w (compatible with your requirements) such that John meets Mary in w. The universal modal operator in (9b) makes it construed that for every world w (compatible with your requirements), John meets Mary in w. When a negative operator occurs in these sentences, it involves the negation of the existence or universality of such worlds. Hence, the two sentences in (10) have logically equal readings, and similarly those in (11) are judged to be equal.

The negation of the existence of the world where John meets Mary has the same logical effect of asserting that for every world w, John does not meet Mary in w. The same relation holds in the sentences in (11).

The paralleled readings in (10) and (11) are not maintained when they occur with a number word as in (12) and (13).

(12a) and (12b), the counterparts of (10a) and (10b), are acceptable, showing the same logical equivalence. However, (13a) and (13b) are not acceptable unlike the sentences in (11). Hence, another question related with semantics of numbers is why the occurrence of the negative operator feeds into an asymmetry in the acceptability of sentences.

1Geurts (2006) argues that number words are used in many different ways and provides a list of usages as follows: (i) a. arithmetical: Five is the fourth Fibonacci number. b. quantifying: Five ducks entered the lobby. c. predicative: These are five buckets. d. adjectival: the five girls e. measure: five pounds of buckwheat f. label: Chanel number five Based on this categorization, Geurts argues that the semantics of number words cannot be just one but specified differently depending on their actual use. In most literature, the quantifying role of numbers is mainly discussed, so other diverse uses of number are not in the scope of the current study.  2Nouwen (2010) notices that numeral modifiers representing maximality or minimality (e.g., at least/minimally and at most/ maximally) cannot occur with numerals having definite amount readings. In (3b), the number of classes that John registered is specifically determined before the utterance, and thus the modifier at least cannot modify three in the sentence. Nouwen accounts for the awkwardness with the notion of Gricean maxims. A definite amount for the number makes the application of the numeral modifier vacuous, which is against the maxim of brevity.

Many analyses on the semantics of numbers follow the Neo-Gricean view and assume that numbers are one-sided and have at least readings. Their exactly readings are due to the result of the application of the quantity maxim. Since the Neo-Gricean view is regarded as dominant, the semantics of numbers is discussed in the same way as scalar quantifiers, scalar adjectives, or comparatives. As discussed in section 2.1, much theoretical and experimental evidence shows that numbers are semantically two-sided. Hence, it is not necessary to review previous analyses on numbers that are based on the Neo-Gricean view of numbers.

In contrast with most previous analyses, Kennedy (in progress) argues for the two-sided interpretations of numbers. When numbers occur without being accompanied by other operators, they are consistently construed as having exactly readings. However, occurring with other modal operators, numbers may be interpreted as one-sided. Kennedy argues that the one-sided readings of numbers are the results of the scopal interactions between numbers and modals. For instance, four documents in (14a) may be interpreted as ‘at most four.’

To get the numeral interpretation of numbers, Kennedy makes use of the operator max, which yields the maximal numberfrom the number(s) in its scope. Then, (14a) is interpreted as (14b) or (14c) depending on the scopal relation between the modal and the number. In the wide scope reading of the modal, (14a) is interpreted that in some world w that is accessible to the contextually given w₀, the maximal number of documents that applicants submit in w is four. No matter which world is selected by the modal, the maximal number of the submitted documents is set to four. This amounts to the exactly reading of the number. On the other hand, in the wide scope reading of the number in (14c), the number of documents that applicants submit may be different in each world, and the max operator of the number maps a set of different numbers to the maximum. Hence, this yields the upper bound reading of the number. Similarly, a sentence with a universal modal has two scopal readings.

In the wide scope reading of the modal in (15b), the sentence is construed that in every world w that is accessible to the contextually given w₀, the maximal number of documents that applicants submit in w is four. The maximal number of documents is restricted to four in all the worlds, so the exactly reading of the number is derived. In contrast, the wide scope reading of the number in (15), each world may have different numbers of documents, and the max operator yields the maximal number that all the worlds share. Hence, this corresponds to the lower bound reading of the number. According to Kennedy, although numbers are lexically two-sided, their upper or lower bound readings may be derived by the scopal interaction with modals.

In Kennedy’s analysis, numbers may have one-sided readings,and which side is bounded is determined by the monotonicity of modal operators they occur with. Since the monotonicity of modal operators is not changeable, minimal and maximal readings of numbers should not be affected by contexts. Although numbers usually have upper bound readings occurring with an Ï operator and lower bound readings occurring with an Å operator, they may have reversed readings depending on contexts.

According to the real world knowledge, buying more books is usually harder to be permitted due to the cost for the books. This makes the minimal reading of three books in (16a) is very awkward. Similarly, having more calories is not helpful in the situation that people try not to gain more weight. Thus, having more calories is less allowable in (16b). Having more cake is also harder to be allowed in most situations, and thus (16c) is more naturally understood in the maximal reading of half the cake.

Just like the sentences in (16), a more prominent reading of (17) is the maximal reading of 60km, i.e., ‘John is allowed to drive at most 60km.’

This is a restriction on the maximal speed for John’s driving. In addition to this maximal reading, a less prominent reading of 60km is also available depending on contexts. In most roads, driving fast is less allowable, which provides an interpretive basis for the maximal reading of the number. However, driving slowly is less allowable in some contexts, say the German autoban. When (17) is used in this situation, what is allowed for John is the lower speed limit of 60 km rather than the upper limit. This is the minimal reading of the number. The monotonicity of the modal operator is not affected by contexts, so the reversed reading of the number in (17) cannot be derived in Kennedy’s analysis. Then, the upper and lower bound readings of numbers are not contributed solely to the monotonicity of modal operators.

The contrasted acceptability shown in (12) and (13) is not discussed by Kennedy. However, given the role of modal monotonicity, it is not easy to imagine an account to be incorporated in his analysis.

To provide a theoretical framework for the interpretations of scalar expressions, Zwartz (1997) and Zwartz & Winter (2000) develop ‘Vector Space Semantics (VSS).’ ‘Vectors,’ newly introduced primitives, are directed line segments in space. With certain operations, vectors form a vector space V over the real numbers R. For a vector space, the following constants and operations are needed:

Vectors are subject to algebraic functions such as addition, subtraction, and multiplication as defined in (18). Any two vectors v and w may be added to make a vector sum v + w. A vector v may have an opposite vector -v, which is specified by the opposition direction. It may be multiplied by a real number.

To see how the algebraic functions work for vectors, we will consider the following vector space.

Two vectors v and w in (19) form a vector sum v + w. The two vectors v and -v in the opposite directions, have the same value, which makes the addition of the vectors 0. Multiplied by a real number like 1.5, a vector w may be expanded to the larger vector 1.5w. Distances in V are represented by a norm function ||, which maps every vector v in V to a non-negative scale in R. For instance, when w has a distance of 4, |w|=4 and |1.5·w|=6.

Zwartz & Winter (2000) argue that vectors are properly used to represent spatial relations between objects. The interpretation of a locative preposition like above involves two relative positions, i.e., one for a ‘reference object’ and the other for a ‘located object.’ For instance, the position of the bird in (20) is determined relative to those of the house and the cloud. The bird is a relative object while the house and the cloud are reference objects to serve as anchoring positions for the bird.

The relative position is represented by a pair of vectors like <w1, v1>, in which w1 specifies the location of the reference object and v1 the position of the located object relative to the reference object. Since two reference objects are mentioned in (20), two located vectors are identified, <w1, v1> for the house and <w2, v2> for the cloud. The location of the bird is specified as <v1+w1, v2+w2>.

Winter (2005) shows how vectors may be properly used to represent adjective interpretations.First, Winter defines a scale, which consists of two elements: (i) a unit vector, i.e., a vector of norm 1, which determines the dimension measured by an adjective and (ii) a set of real numbers that specify the legitimate values along this dimension. A context determines how large a unit vector is, and a scale defined by a unit vector is discrete. To incorporate a contextual value for a scalar reading, a standard value is postulated. The interpretation of a scalar adjective like tall is affected by diverse factors such as sex, age, race, etc. Hence, a standard value represents a contextually provided criterion for tallness. When a standard value for tallness is set to 5 feet, any value greater than 5 in the height scale u_H is considered as part of tall due to its upward monotonicity. The semantics of tall is given in (21), in which t₀ and t represent the real numbers of the standard value and a measured value in a unit vector.

Tall denotes a set of located vectors, where the first coordinate is set to zero in the height scale and the second vector is greater than the standard value. Then, anyone who has a degree greater than 5 in the height scale, or is taller than 5, is considered tall. Short, the antonymous adjective of tall, is defined in a downward scale -H = <-u_H, (-∞, 0)>. In the situation that the standard value for shortness is -3, short is interpreted as in (22).3

Any vector that is greater than -3 in the downward scale or less than 3 in the upward scale is included in the interpretation of short. Then, anyone who is shorter than 3 by unit vector, or 3 feet, is considered short.

In this section, I discuss in the framework of VSS how numbers are assigned one-sided readings occurring with modal operators. While number words are semantically two-side bound, their one-sided readings are attributed to the monotonicity of modal operators. The two-sided readings of numbers make it possible that either upward or downward scales are selected for their interpretations depending on contexts.

When a sentence does not encompass any degree expression, its interpretation is to assert the truth or the existence of the event that the sentence describes. For example, (23a) asserts the proposition that John drove or the existence of John’s driving event depending on theories.

When a number word occurs in a sentence as in (23b), the truth of the sentence is not checked only by the existence of John’s driving event but the event should meet a specific property of 60km. To assert this event property, a scalar structure for speed is needed. As noted in section2.1, number words are two-sided and have exactly readings. This means that numbers themselves are not monotoneand that both upward and downward scalar structures are available for the interpretations of numbers.

For a given pair of antonymous scalar adjectives, the upward monotone adjective is unmarked. For example, the scalar adjectives tall and short make an antonymous pair, interpreted in an upward scale and a downward scale, respectively. In this pair, the upward adjective tall is unmarked and used to represent tallness. In the same spirit, although number words are not monotone, unmarked upward scales are adopted for their interpretations unless there are other semantic requirements for downward scales. Based on this assumption, (23b) is interpreted as in (24a), which is based on the vector representation in (24b).4

(24a) is a proposition that John drives at the speed of 60 km. Since John’s driving is measured by kilometer, the unit vector u_S is understood as kilometer. Then, 60 km denotes a located vector in the upward scale, which is a measurement from 0 to 60 multiplied by the unit vector, i.e., kilometer. Along with this unmarked reading, the marked reading of (24a) is also possible in the downward speed scale -u_S. Since numbers are not monotone, the interpretation of (24a) is not much different no matter which scale is taken.

In contrast with the two-sided reading of (24a), 60 km in (25a) is bound only in its upper limit as paraphrased in (25b).

When the existential modal operator takes wide scope over the number, (25a) is construed that it is possible that John drives 60 km. In ordinary contexts, the monotone reading of the sentence is that the upper limit of John’s driving is 60 km. As discussed above, numbers themselves are not monotone, and thus both upward and downward scales are available for the interpretations. However, the unmarked scale is upward if there is no contextual requirement for the opposite. Hence, (25a) is construed in the upward speed scale, which is represented in (26a).

Since allow is a downward operator, variables in its scope are affected by its downward monotonicity. A variable for worlds and a variable for speed vectors lie in the scope of the operator, sothey are downward monotone. Then, all the vectors that are less than <0,60·u_S> are entailed to be allowed. This leads to the upper bound reading of the sentence as in (26b). There is some world w that is accessible to the contextually given world w₀ such that John drives in w at the speed of d, which ranges from 0 to 60 km.

Along with the unmarked interpretation in (26b), (25a) may also have a marked reading. Suppose that driving slowly is problematic and harder to be permitted, e.g., the German autoban. In this situation, how slowly people drive is a main concern, and (27a) is more properly construed like the paraphrase in (27b).

Since slow driving is a problem, what is allowed in (27a) is the lower speed limit. This marked interpretation is legitimately represented in a downward scale as in (28a).

When there is no upper limit for speed, the scale is from the infinity to zero. On the other hand, if the context has a high speed limit t₀, say 100 km, then the scale is made of vectors moving from 100 to zero. Since the number is still within the scope of the modal operator, the number lies in the downward monotonicity of the operator. Hence, (28a) shows the downward speed scale with downward monotone vectors. All the vectors that are less than <0,-60ㆍ-u_S> such as <0,-70ㆍ-u_S>, <0,-80ㆍ-u_S>, etc., are included in the speed allowed for John in (28b). Unlike Kennedy (in progress), scales in VSS are two directional, and which scale is adopted is affected by contexts. Thus, the less prominent reading of (27a) is also derived.

Numerals are understood as taking scope. This implies that the number word may take wide scope over the modal operator. A third reading for (29a) is the wide scope reading of 60 km over the modal.

Note that the monotone reading of the number is due to the monotonicity of the operator. When the number takes wide scope, it is not affected by the operator. Then, 60 km in this reading is non-monotone, and the relevant vector space is the one in (24b). The resulting reading is (29b), which asserts for the existence of a world in which John drives (exactly) 60 km. The non-monotonicity of the number does not exclude the selection of the downward scale for the interpretation. However, just as in (24a), the downward scaled interpretation for (29a) is more or less the same. Although the directionality is reversed, the vector has a value of 60. Since the wide scope reading of a number word is non-monotone, it is not discussed further in the following study.

When a number word occurs with the universal modal as in (30a), it is interpreted in the same way except that the number is upward monotone. The unmarked reading of (30a) is the lower bound reading of 60 km as in (30b) while the marked one is its upper bound reading as in (39c).

In the unmarked reading, how fast people drive is a main concern according to the real world knowledge. Thus, the speed required to people in every ideal world is the lower limit. On the other hand, when driving slowly makes a problem, the requirement for people in every ideal world is the upper limit. Just like the sentence with the existential modal, the unmarked reading of (30a) is construed in the upward scale as in (31a) whereas the marked one is interpreted in the downward scale as in (31b).

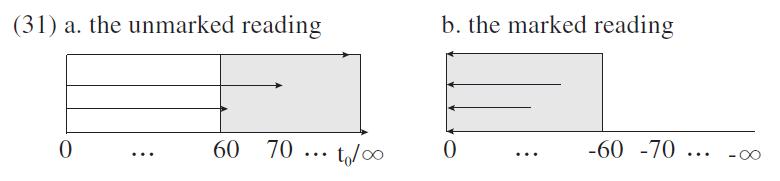
What is different from (26a) and (28a) is that the vectors in (31a) and (31b) are upward monotone due to the upward monotonicity of the operator. Hence, in the unmarked reading of (31a), all the vectors that are greater than<0, 60ㆍu_S> are entailed by the sentence. On the other hand, in the marked reading of (31b), all the vectors that are greater than <0,-60ㆍ-u_S> in the downward scale, namely <0,-50ㆍ-u_S>, <0,-40ㆍ-u_S>, etc., are entailed by the sentence. The vector representations in (31) lead to the readings in (32).

(32a) says that for every world w that is accessible to the contextually given world w₀, John drives at the speed of 60 km or higher. When the context provides a contextual value t₀ for the high speed limit like 100 km, the vector in (32a) is limited. The marked reading in (32b) is an assertion for the upper speed limit of 60 km for John’s driving.

When a sentence does not include any monotone expression, the occurrence of a negative operator plays the role of negating the proposition. However, in a sentence with one, it has the effect of negating the monotonicity.

Not in (33a) negates the existence of a world where John meets Mary, which amounts to saying that in every world w, John does not meet Mary in w. This is the universal reading of modality, which is why (33a) and (33b) are logically equivalent. Similarly, the same equivalence relationholds between the sentences in (34).

Occurring with a scalar expression, a negative operator reverses the direction of its scale. According to Zwarts & Winter (2000), antonymous scalar predicates are mapped into reversed directions of scales in VSS as shown by the contrast of tall and short in (21) and (22). The change of direction for a scale is not confined to antonymous predicates but applies to a pair of positive and negative predicates. Say that John, Bill, and Tom are 5 feet, 5.5 feet, and 6 feet tall, respectively. If John is tall, it is entailed that Bill and Tom are tall. This is upward monotone. On the other hand, if Tom is not tall, then Bill and John are also entailed not to be tall. The negative predicate not tall shows downward monotonicity. Thus, I argue that part of the semantic role of a negative operator is to change the direction of a scale for an expression in its scope. While tall is defined in an upward scale, not tall is interpreted in a downward scale like short. In a situation that five feet is the criterion for tallness, the standard value of t₀ is set to 5, and the semantics of not tall is defined as in (35).6

Given the roles of a negative operator, dual changes are incurred in sentences accompanied by both a modal and a scalar expression. One is to negate the modal assertion and the other is to reverse the direction of the scalar expression. For example, when not takes wide scope over the modal and the number word in (36), it has the effect of negating the existentiality of the modal and reversing the scalar direction for the number to downward.

Just as tall and not tall are construed in an upward scale and a downward scale, respectively, 60 km and not 60 km are assigned opposite directions of scales. Since (36) includes three scopal expressions, multiple relations are available for the sentence. However, the most prominent reading is the one following their hierarchical structure. (cf. Musolino 2009) Then, not takes scope over allow and 60 km, and allow takes wide scope over 60 km. Since 60 km lies in the scope of the negative, the direction of a scale is changed to downward. However, the number is still in the scope of the modal operator, so the downward monotonicity of the number is maintained.

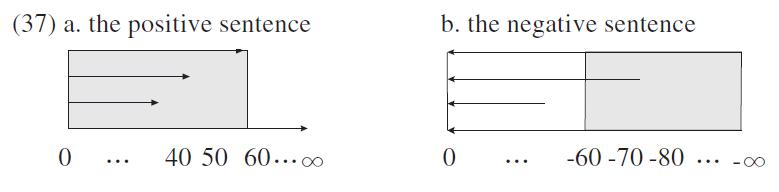
The focus of negation in (36) is not on the event of driving but on the speed. John can still drive but not at the speed of 60 km. Hence, what is negated is the vectors entailed by the positive counterpart sentence John is allowed to drive 60 km. In the unmarked reading, 60 km in this positive sentence includes all the vectors that are greater than <0, 60ㆍu_S>, which are in the shaded box in (37a).

The scale in (37a) is upward and 60 km is downward monotone. The negative sentence in (36) is interpreted in the downward scale as in (37b), and 60 km is still downward monotone. Hence, all the vectors that lie in the shaded box in (37b) are negated. The negated vectors are exactly the opposite of the positive counterpart in (37a), and its formal representation is given in (38).

(38) says that there is no world w that is accessible to the contextually given world w₀ such that John drives in w at the speed of d, which is less than 60 km in the downward scale. To put it in the upward scale, (38) is logically similar to say that John is not allowed to drive greater than 60 km. This is a prohibition on driving fast. Hence, the negation in (36) provides a clear requirement for the ideal behavior for John.

As noted in section 2.2, when a universal modal occurs in a negated sentence, it is not as natural as an existential modal.

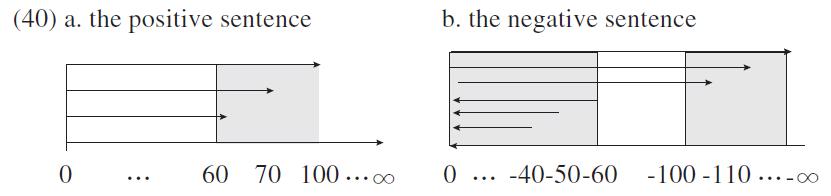
In the most prominent reading, not takes wide scope over require and 60 km, and require takes scope over 60 km. The wide scope reading of not results in the change of the monotonicity of the modal and the reversed direction of the scale for the number. Not require has existential force on worlds, and a relevant scale for 60 km is interpreted in the downward scale. Since 60 km is in the scope of require, it is upward monotone. As discussed in section 4.3, there are two readings for the positive counterpart John is required to drive 60 km. One is that there is no upper limit for driving in the context. Then, this positive sentence applies to all the vectors that are greater than 60 km in the upward scale and asserts that John is required to drive greater than 60 km. When these vectors are negated, the ideal behavior required for John is to drive less than 60 km. (39) sounds acceptable in this reading. The other reading for the positive sentence is that there is an upper limit for driving, say 100 km. Since the vector space for this positive sentence lies in the middle of the scale, the set of vectors to be negated is divided as shown in the shaded box of (40b).

When the negation in (39) applies to this divided set of vectors, it should have an effect similar to the proposition that John is not required to drive less than 60 km and greater than 100 km. Technically speaking, there is no scalar structure to include this split set of vectors because of their different monotonicity. A more serious problem is that there is no consistent requirement of ideal behavior for John. It is not clear that what is prohibited on John’s driving between driving slowly or driving fast. The awkwardness of (39) is attributed to this incoherent prohibition on John, which is represented by the divided set of vectors.

We have discussed the unmarked readings of (36) and (39). As noted in section 4.2, these sentences may be interpreted in the marked situation, which is based on the reversed direction of a scale. The change of the scalar direction yields a complementary set of vectors. Then, the negation of the existential sentence in (36) is interpreted with a divided set of vectors while that of the universal sentence in (39) is construed with a coherent set of vectors. The acceptability judgment of the sentences will be also the opposite from the ones in the unmarked case. Since the primary reading is derived in the unmarked situation, the overall judgment is that (36) sounds more acceptable than (39). However, when a context gears strongly for the marked case, the judgment for the sentences will be different.Part of the reason that (39) is not completely unacceptable but just quite awkward is due to the existence of this secondary reading.

When a sentence is accompanied by a number word, the negation of this sentence focuses on the degree or amount of the number denotation.

A sentence without a number in (41a) involves the negation of the proposition that John drove or the denial of the existence of the event of John’s driving itself. However, when the sentence is followed by the number word as in (41b), the focus of negation does not lie on the event but on the degree of the number.7 As discussed in Kwak (2010), when the negative operator applies to the number in VSS, what is negated is not the whole numeral value of 60 km but the excess or the shortage between 60 km and the actual speed of John’s driving.8 Suppose that John actually drove 55km. Then, the negation of (41b) asserts that the excess of 5 km is not true with the actual driving. On the other hand, if John drove 65 km, the negation asserts the shortage of 5 km from the actual speed is not true. Hence, the concept of standard value t₀ is needed in interpreting the negation of a degree sentence.9

The formal representation in (42a) says that there is a set of worlds w in which John did not drive at the speed from t₀ and 60 km. Since the negation is about the excess or shortage value from the standard value, i.e., the actual speed of John’s driving, the negated reading of (41b) is ambiguous depending on the relative locality of the negated value and the standard value. This ambiguity of the negated sentence is instantiated by the selection of a scalar structure. If the standard value is lower than the negated value, then an upward scale is selected for the interpretation. For example, when the actual speed is 55 km, t₀ is 55 and the located vector is <55ㆍu_S,5ㆍu_S>. Then, the sentence asserts that the excess amount of 5 km from 55 km is not true with John’s driving. On the other hand, when the standard value is higher than the negated value, a downward scale is needed for the interpretation. As represented in (42b), the sentence negates a shortage value from the actual driving speed.

When negative predicates occur in the scope of modality as in (43a), it is assigned the unmarked interpretation in (43b) or the marked one in (43c).

According to (43b), when the standard value t₀ or the ideal speed is 59 km, what is negated is the vector <59ㆍu_S, 1ㆍu_S>. Since the number is in the scope of the upward monotonicity of the modal, all the vectors that is greater than <59ㆍu_S, 1ㆍu_S> are negated, e.g., <59ㆍu_S, 11ㆍu_S> (i.e., 70 km), <59ㆍu_S, 21ㆍu_S> (i.e., 80 km) etc. This interpretation is logically equivalent to the proposition that John is required not to drive greater than 60 km. The ideal behavior required for John is to drive slowly. On the other hand, in the marked situation such that the standard value is higher than 60 km, namely 61 km, the downward scale is taken for the interpretation. All the vectors that is greater than <-61ㆍ-u_s, -1ㆍ-u_s>, e.g., <-61ㆍ-u_s, -11ㆍ-u_s> (i.e., 50 km), <-61ㆍ-u_s, -21ㆍ-u_s> (i.e., 40 km), etc., are negated. This reading equals to the proposition that John is required not to drive less than 60 km. Now the ideal behavior required for John is to drive fast.

In contrast with the clear requirement for the ideal behavior for John in (43), the modal reading in (44a) is not straightforward.

Since (44a) is different from (43a) only by the modal operator, the formal interpretation in (44b) is identical to (43b) except for the modality. In this unmarked reading, the standard value is lower than the negated numeral. Say that the standard value or the ideal speed is 59 km. Since 60 km is in the scope of the existential modal, it is downward monotone. Hence, all the vectors that is less than <59ㆍu_S, 1ㆍu_S> (i.e., 60 km) and greater than the ideal speed (i.e., 59 km) are negated. Only the vectors in this narrow range are negated, so (44a) is similar to the reading that John is allowed to drive less than 59 km and to drive greater than 60 km. If the speed does not lie between 59 km and 60 km, most of John’s driving is allowed. Additionally, the ideal behavior for John is divided between driving fast and driving slowly. Hence, the sentence does not have coherence for deontic modality. Similarly, when the standard value is higher than 60 km, the same narrow range of vectors in the downward scale are negated in (44c). This also has the same incoherence problem as the unmarked case.

In addition to the readings discussed above, (43a) and (44a) have the inversed scope readings in which the negative operator takes scope over the modal operators. In this inversed relation, the negative operator does not negate the speed of 60 km but the monotonicity of the modal operators. Then, the interpretation of (43a) is equal to the awkward sentence John is not required to drive 60 km. Likewise, (44a) is equal to the acceptable sentence John is not allowed to drive 60 km. The sentences in this inversed scopal relation have opposite judgments. In the current study, the inversed scope relations change the monotonicity of the modal operator, and thus the opposite judgments naturally follow as shown by the discussion in the previous section.

3The minus number in the downward scale does not mean that the degree has a minus value. For instance, -3 with the unit vector of foot does not refer to -3 feet. The minus number shows that the degree moves in a downward scale which starts from a large number and moves to a small number. This is why the degree in the downward scale may be reinterpreted in the upward scale in (22).  4The semantics of tense is not considered in this study for the simplicity of discussion. The variable w in (24) is over possible worlds while win deontic modal sentences is over ideal worlds. I do not distinguish these two types of variables in this study.  5When the vectors in the downward scale are reinterpreted in the upward scale, the interpretation in (28b) is represented as follows. (i) ∃w∈Accwo[drivew(d)(j) ^ d ∈ {<0, tㆍus>: 60≤t (≤100/∞}]  6Vectors for short make a smaller set than those for not tall because the standard value for short is lower than that for tall. When shorter than 5 feet is understood as not tall, the criterion for short height is usually lower than 5 feet. Hence, although not tall and short are construed in the same downward height scale, their standard values are different. This distinction makes the meaning difference between not tall and short.  7Since both of the negative operator and the number take scope, (42) has another reading in which the number takes wide scope over the negative. This wide scope reading is paraphrased that 60 km is not the one that John drove. Note that numbers are two-sided and non-monotone. Hence, the wide scope reading of 60 km does not have entailments about speed. It is just a contrasted reading such that 60 km is not the correct speed that John drove but something else.  8This vector space interpretation of a negated number is useful to account for distinct entailments depending on the contextual value. See Kwak (2010) for more discussion.  9This is a revised interpretation of the negative degree sentence, which is proposed in Kwak (2011). Kwak (2010) suggests one differential reading, which is assumed to be instantiated on either an upward or downward scale. This is too vague and not guaranteed that the interpretation is always defined. Thus, Kwak (2011) proposes two differential reading of different monotonicity as in (42).

The semantics of number words was not paid much attention to because they were treated like other scalar quantifiers. They were considered to be one-sided and interpreted to have at-least readings. Their exactly readings, which are two-sided, were derived by scalar implicature. This Neo-Gricean view on numbers has been challenged by theoretical and experimental study over the past decade. The explicit specification of one-sided readings is not allowed for numbers occurring with expressions for a definite amount, and apparent scalar implicature is not possible with a distributive predicate. Experimental evidence also shows that both children and adults consistently take two-sided readings of numbers instead of cancelling scalar implicature.

In spite of the evidence for the two-sided readings of numbers, they appear to have one-sided readings occurring with modal operators. Numbers in the scope of an existential modal have at-most readings while those in the scope of a universal modal have at-least readings. Moreover, the occurrence of negative operator may worsen the acceptability of sentences with a modal and a number. Kennedy (in progress) suggests that the one-sided readings of numbers are the results of scopal interactions between numbers and modals. I have argued that the monotonicity of numbers may be reversed depending on contexts, and that these less prominent readings cannot be derived in Kennedy’s analysis.

To derive one-sided readings of numbers, I have discussed the semantics of modals and numbers in the framework of Vector Space Semantics (VSS). Scalar expressions are interpreted in directed scales in VSS, and upward or downward scales may be selected by the monotonicity of scalar expressions. I have suggested that numbers are affected by the monotonicity of modals although they are lexically two-sided. Numbers in the scope of an existential modal are downward monotone while those in the scope of a universal modal are upward monotone. Along with the monotonicity of numbers, I have argued that which direction of scale is taken for an interpretation may be affected by context. In an unmarked situation, an upward scale is adopted for the interpretation of a positive sentence. However, a downward scale may also be used in a marked situation. Two directional scales and the monotonicity of numbers in a modal scope provide an explanation for the different interpretations of numbers in modal sentences. Given the semantics of numbers, I haveshown that the insertion of a negative operator may incur a split set of vectors for a modal sentence with a number. The incoherent set of vectors is construed as the lack of an ideal behavior, which does not fit with the semantics of a deontic modal operator. With the basic notions of monotonicity and scope relations between modals, numbers, and negative operators, I have derived contextually affected interpretations of modal sentences with numbers and provided an account for the awkwardness incurred by the insertion of a negative operator.