In “A Computational Foundation for the Study of Cognition” (forthcoming) David Chalmers articulates, justifies and defends the computational sufficiency thesis (CST). CST states that “the right kind of computational structure suffices for the possession of a mind, and for the possession of a wide variety of mental properties.” Chalmers addresses claims about universal implementation, namely, that (almost) every physical system implements (roughly) every computation (Putnam 1988; Searle 1992). These claims appear to challenge CST: If every physical system implements every computational structure, then (if CST is true) every physical system implements the computational structure that suffices for cognition (“a possession of a mind”). Hence, every physical system is a cognitive system. In other words, if CST is true then rocks, chairs and planets have the same kind of cognition that we do Chalmers rgues, however, that the antecedent of the first conditional (i.e., universal implementation) is false; he offers instead a theory of implementation that avoids the pitfalls of universal implementation.

My aim here is to argue that Chalmers’s theory of implementation does not block a different challenge to CST. The challenge, roughly, is that some possible physical systems simultaneously implement different computational structures (or different states of the same computational structure) that suffice for cognition; hence these systems simultaneously possess different minds. Chalmers admits this possibility elsewhere (1996). But I argue that it is more than just a remote, implausible scenario, and that it renders CST less plausible.

Chalmers writes that by justifying CST “we can see that the foundations of artificial intelligence and computational cognitive science are solid.” I wish to emphasize that my argument against CST is not meant to undermine in any way the prospects of the theoretical work in brain and cognitive sciences.1 My conclusion, rather, is that CST is not the way to construe the conceptual foundations of computational brain and cognitive sciences. While I do not offer here an alternative conceptual account, I have outlined one elsewhere (Shagrir 2006; 2010), and intend to develop it in greater detail in future.

The paper has three parts. In the next section I discuss the notion of implementation. I point out that Chalmers’s theory is consistent with the nomological possibility of physical systems that simultaneously implement different complex computational structures. In Section 3 I say something about the current status of CST. In Section 4 I argue that the possibility of simultaneous implementation weakens the case of CST.

1This is in sharp contrast to Searle, who concludes from his universal implementation argument that “there is no way that computational cognitive science could ever be a natural science” (1992: 212).

Hilary Putnam (1988) advances the claim that every physical system that satisfies very minimal conditions implements every finite state automaton. John Searle (1992) argues that the wall behind him implements the Wordstar program. Chalmers argues that both Putnam and Searle assume an unconstrained notion of implementation, one that falls short of satisfying fairly minimal conditions, such as certain counterfactuals. Chalmers (1996) formulates his conditions on implementation in some detail. He further distinguishes between a finite state automaton (FSA) and a combinatorial state automaton (CSA) whose states are combinations of vectors of parameters, or sub-states. When these conditions are in place, we see that a rock does not implement every finite state automaton; it apparently does not implement even a single CSA.2

I do not dispute these claims. Moreover, I agree with Chalmers on further claims he makes concerning implementation. One claim is that every system apparently implements an FSA: A rock implements a trivial onestate automaton. Another claim is that many physical systems typically implement more than one FSA. In particular, if a system implements a more complex FSA, it typically simultaneously implements simpler FSAs. A third claim is that relatively few physical systems implement very complex CSAs. In particular, very few physical systems implement a CSA that (if CST is true) suffices for cognition. Chalmers points out that the chance of an arbitrary physical system implementing such a CSA is close to nil. I agree with this too.

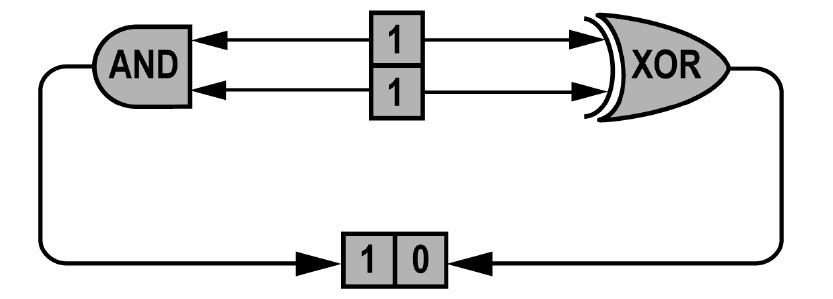
Nevertheless, I want to point out that one could easily construct systems that simultaneously implement different complex CSAs. I will illustrate this claim with the example of a simple automaton.3 The description I use is somewhat different from the one used by Chalmers. Chalmers describes automata in terms of “total states.” I describe them in terms of gates (or “neural cells”), which are the bases of real digital computing. The two descriptions are equivalent.4

Consider a physical system P that works as follows: It emits 5-10 volts if it receives voltages greater than 5 from each of the two input channels, and 0-5 volts otherwise.5 Assigning ‘0’ to emission/reception of 0-5 volts and ‘1’ to emission/reception of 5-10 volts, the physical gate implements the logical AND-gate: ‘0,’ ‘0’ → ‘0’; ‘0,’ ‘1’ → ’0’; ‘1,’ ‘0’ → ‘0’; ‘1,’ ‘1’ → ‘1.’

Let us suppose it turns out that flip detectors of P are actually tri-stable. Imagine, for example, that P emits 5-10 volts if it receives voltages greater than 5 from each of the two input channels; 0-2.5 volts if it receives under 2.5 volts from each input channel; and 2.5-5 volts otherwise. Let us now assign the symbol ‘0’ to emission/reception of under 2.5 volts and ‘1’ to emission/ reception of 2.5-10 volts. Under this assignment, P is now implementing the OR-gate: ‘0,’ ‘0’ → ‘0’; ‘0,’ ‘1’ → ‘1’; ‘1,’ ‘0’ → ‘1’; ‘1,’ ‘1’ → ‘1.’6

The result is that the very same physical system P simultaneously implements two distinct logical gates. The main difference from Putnam’s example is that this implementation is constructed through the very same physical properties of P, namely, its voltages. Another difference is that in the Putnam case there is an arbitrary mapping between different physical states and the same states of the automaton. In our case, we couple the same physical properties of P to the same inputs/outputs of the gate. The different implementations result from coupling different voltages (across implementations, not within implementations) to the same inputs/outputs. But within implementations, relative to the initial assignment, each logical gate reflects the causal structure of P. In this respect, we have a fairly standard implementation of logical gates, which satisfies the conditions set by Chalmers on implementation.

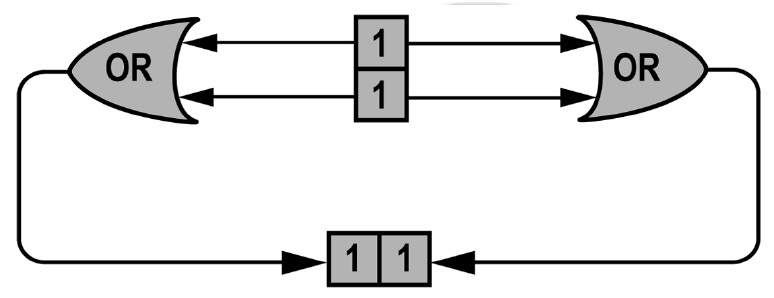
We could create other dual gates in a similar way. Consider a physical system Q that emits 5-10 volts if it receives over 5 volts from exactly one input channel and 0-5 volts otherwise. Under the assignment of ‘0’ to emission/ reception of 0-5 volts and ‘1’ to emission/reception of 5-10 volts, Q implements an XOR-gate: ‘0,’ ‘0’ → ‘0’; ‘0,’ ‘1’ → ‘1’; ‘1,’ ‘0’ → ‘1’; ‘1,’ ‘1’ → ‘0.’ Suppose, as before, that flip detectors of Q are tri-stable. Suppose that Q emits 5-10 volts if it receives voltages higher than 5 from exactly one input channel; 0-2.5 volts if it receives under 2.5 volts from each input channel; and 2.5-5 volts otherwise. Assigning the symbol ‘0’ to emission/ reception of under 2.5 volts and ‘1’ to emission/reception of 2.5-10 volts, Q is now implementing the OR-gate. In a similar way I can have a physical system R that has the dual gates of NAND and XOR, as well as others.7

Yet another example is of a physical system S. This system emits 5-10 volts if it receives over 5 volts from at least one input channel and 0-5 volts otherwise. Under the assignment of ‘0’ to emission/reception of 0-5 volts and ‘1’ to emission/reception of 5-10 volts, S implements an OR-gate. As in the previous cases, it turns out that flip detectors of S are actually tristable. S emits 5-10 volts if it receives voltages higher than 5 from at least one of the two input channels; 0-2.5 volts if it receives under 2.5 volts from both input channels; and 2.5-5 volts otherwise. Assigning the symbol ‘0’ to emission/reception of under 2.5 volts and ‘1’ to emission/reception of 2.5-10 volts, S is now implementing the OR-gate (again). This case is interesting in that the two implemented OR-gates might be in different “total states” under the same physical conditions. If, for example, the inputs are 1 volt in one channel and 3 volts in the other (and the output is, say, 3 volts), then this very same physical run simultaneously implements the ‘0,’ ‘0’ → ‘0’ mapping under the first implemented OR-gate, but the ‘0,’ ‘1’ → ‘1’ mapping under the second implemented OR-gate.

I do not claim that these physical systems implement every logical gate. They certainly do not implement a complex CSA. The point I want to emphasize is quite different. You can use these kinds of physical gates (i.e., P, Q, R, S and the like), as building blocks of other physical systems that simultaneously implement very complex automata. As an illustration, let us construct Ned Block’s device for computing the addition of two-digit numbers (Block 1990); the implemented system can be seen as a very simple automaton (fig. 1). Using our physical gates P and Q as building blocks, this very same device also implements a very different automaton (fig. 2). The more general point is that if you want to implement a zillion-gate automaton, you can use these and other gates to implement another automaton of “the same degree”, whereas “the same degree” means the same number of logical gates. Automata that include finite and infinite memory (as in Turing machines) are no obstacle to this result; we can individuate the 0’s and 1’s in the memory the same way that we individuate the inputs and outputs. Thus “same degree” also means the “same amount of memory.”

Note that I do not claim that this ability is shared by every physical system. We can assume that physical systems often implement only one automaton of the same degree. It might also be the case that, technologically speaking, it will be ineffective and very costly to use these tri-stable gates (though I can certainly see some technological advantages). The point is philosophical: If implementing some CSA suffices for the possession of a mind, then I can construct a physical system that simultaneously implements this CSA and another CSA of the same degree. I can also construct two instances of the same CSA, each of which is in a different total state. These constructions are not just a logical or metaphysical possibility. These constructions are nomological possibilities; in all likelihood, they are also technologically feasible, if we can construct a CSA that suffices for a mind.

One may point out that these physical systems always implement a deeper, “more complex,” automaton that entails the simultaneous implementation of the “less complex” automata. Thus the system P in fact implements a tri-value logical gate that entails both the AND-gate and the OR-gate. The same goes for the implementation of the more complex CSAs: There is always a “maximally complex” automaton that entails the implementations of the “less complex” automata. I do not deny this observation. My point at this junction is just this: If the implementation of a certain CSA suffices for a mind, then I can construct a physical system that implements a maximally complex automaton that entails the implementations of this CSA (hence, a mind) and another automaton of the same degree. This result, at any rate, is consistent with Chalmers’s theory of implementation.

2See also Chrisley (1994) and Copeland (1996).  3The original example is presented in an earlier paper (Shagrir 2001).  4See Minsky (1967) who invokes both descriptions (as for the second description, he presents these and other gates as McCulloch and Pitts “cells”) and demonstrates the equivalence relations between them (the proof is on pp. 55-58).  5We can assume for purposes of stability that the reception/emission is significantly of less/more than 5 volts.  6See also Sprevak (2010), who presents this result more elegantly without invoking tri-stable flip-detectors.  7Shagrir (2012).

Chalmers does not explicate the sense in which computational structure suffices for cognition, e.g., identity, entailment, emergence and so on. It seems that he is deliberately neutral about this question. Keeping this metaphysical neutrality, we can express the sufficiency claim in terms of supervenience: Mind supervenes on computational structure. Chalmers points out that some mental features, e.g., knowledge, might not supervene on (internal) computational structure, as they depend on extrinsic, perhaps non-computational, properties.8 But he suggests that cognitive (“psychological”) and phenomenal properties supervene on computational properties. Cognitive properties, according to Chalmers, are defined by their causal roles. Phenomenal properties are not defined by causal role, but they “can be seen to be organizational invariants” (forthcoming). To put it in terms of supervenience, phenomenal properties supervene on organizational invariants (elsewhere Chalmers says that “any two functionally isomorphic systems must have the same sort of experiences” (1995a: 215). However, the modal strength of supervenience is not logical, conceptual or even metaphysical. The modal operators express empirical, physical or nomological possibility/necessity (Chalmers 1995a).

It should be noted that supporters of CST might disagree with Chalmers about the details. One could hold the view according to which a certain computational structure suffices for having a mind, but this computational structure does not fix all mental properties. Thus one might hold that having a certain computational structure ensures that one is thinking, but this structure does not fix the psychological content of one’s thoughts. One could also hold the view that computational structure does not fix one’s phenomenological properties. Thus one could argue that CST is consistent with the nomological possibility of spectrally inverted twins who share the same computational structure. For the purposes of this paper, however, I identify CST with what Chalmers has said about the relationship between computational structure and mentality.

Chalmers provides a justification for CST. As I understand him, the justification is an argument that consists of three premises: 1. Cognitive capacity (mind) and (most of) its properties supervene on the causal structure of the (implementing) system, e.g., brain. 2. The pertinent causal structure consists in causal topology or, respectively, organizational invariant properties. 3. The causal topology of a system is fixed by some computational structure. Hence cognitive capacity (mind) is fixed by an implementation of some computational structure; presumably, some complex CSA.

The first premise is very reasonable: Many (perhaps all) capacities, cognitive or not, are grounded in causal structure. This, at any rate, is the claim of mechanistic philosophers of science.9 The third premise makes sense too, at least after reading Chalmers on it (section 3.3). The second premise is the controversial one. In the non-cognitive cases, the causal structure that grounds a certain capacity essentially includes non-organizationalinvariant properties, i.e., specific physical, chemical and biological properties. In those cases, organizational invariants are not enough. These noncognitive cases motivate the distinction between computer simulation and the real (simulated) thing. A computer simulation can have the same causal topology as that of hurricanes, but no real hurricanes take place inside the simulating computer. Why assume that the perfect simulation of the causal topology of the brain (i.e., implementing computational structure) suffices for real cognition?

At this point intuitions clash, especially when it comes to phenomenal properties. I share with Chalmers the intuition that (at least some) siliconmade brains and neural-made brains, which have the same computational structure, produce the same cognitive properties and even the same experience, say the sensation of red. But this intuition, by itself, falls short of showing that cognitive and phenomenal properties supervene on organizational variants. First, the two brains share physical properties. They both invoke electrical properties that might play an essential role in producing phenomenal properties. Second, even if the two brains, silicon and neural, do not share (relevant) physical properties, this does not exclude the possibility of other computationally identical “brains” that do not produce the experience of red. Indeed, others have argued that systems with the same computational structure—e.g., certain arrangements of the people of China (Block 1978), the Chinese room/gym (Searle 1990), and so on —produce no phenomenal properties at all. Chalmers contends that these arguments against CST are not convincing. I agree with him about that. He also advances the “dancing qualia” and “fading qualia” arguments whose conclusion is that phenomenal properties supervene on organizational invariants (Chalmers 1995b). But these arguments essentially depend on the assumption that cognitive properties (e.g., noticing) are organizational invariants, and the arguments for this assumption have been challenged too.10

The upshot is that the debate about the validity of CST is far from settled. My aim in the next part is to provide yet another, but very different, argument against it.

8There are those, however, who argue that the pertinent computational structure extends all the way to the environment (Wilson 1994).  9See, for example, Bechtel and Richardson (1993/2010), Bogen and Woodward (1988), and Craver (2007).

The challenge to CST rests on the nomological possibility of a physical system that simultaneously implements two different minds. By “different minds” I mean two entire minds; these can be two minds that are of different types, or two different instances of the same mind.

Let me start by explicating some of the assumptions underlying CST. CST, as we have seen, is the view that computational structure suffices for possessing a mind (at least in the sense that a mind nomologically supervenes on computational structure). Then two creatures that implement the same structure cannot differ in cognition, namely one having a mind and the other not. The friends of CST assume, more or less explicitly, that having a mind requires the implementation of a “very complex” CSA, perhaps an infinite machine. This automaton might be equipped with more features: Ability to solve (or approximate a solution for) certain problems in polynomial-bounded time; some universality features; ability to support compositionality and productivity; and so on. Let us call an automaton that underlies a mind a COG-CSA.

Another assumption is that there is more than one type of COG-CSA. We can assume that all human minds supervene on the very same COG-CSA (or closely related automata that under further abstraction can be seen as the same computational structure). We can also assume that monkeys, dolphins and other animals implement automata that in one way or another are derivatives of COG-CSA. But I guess that it would be overly anthropocentric to claim that every (possible) natural intelligent creature, perhaps living on very remote planets, every artificial (say, silicon-made) intelligent creature, and every intelligent divine creature, if there are any, implements the very same COG-CSA. I take it that the CST is not committed to this thesis.

Yet another assumption concerns cognitive states, events, processes and the like, those that supervene on computational structure. The assumption is that every difference in cognitive states depends on a difference in the total states of the (implemented) COG-CSA(s), be it the total states of different COG-CSAs, or the total states of the same COG-CSA. Thus take phenomenal properties. If you experience the ball in front of you as wholly blue and I experience the ball in front of me as wholly red, then we must be in different total states of COG-CSA (whether the same or different COG-CSA). The same goes for me having different phenomenal experiences at different times. The difference in my phenomenal experiences depends on being in a different total state of (the implemented) COG-CSA.

The last assumption is that if a physical system simultaneously implements different COG-CSAs, or two different instances of the same COGCSA, then it possesses two different entire minds. Establishing this assumption largely depends upon how one individuates minds, and upon how this individuation scheme relates to the computational structure on which it supervenes. But I do not think we can say that the two different COG-CSAs are simply two different computational descriptions or perspectives of the same mind. CST is committed to more than that. Let us say that a physical system simultaneously implements two COG-CSAs, COG-CSA₁ and COG-CSA₂ (these can be two instances of the same COG-CSA that are in different total states). Let us also say that COG-CSA₁ is the subvenient structure of my mind, and COG-CSA₂ is the subvenient structure of your mind. It seems that the supervenience claim requires that this physical system will simultaneously possess my entire mind and your entire mind, whatever this means. But it cannot mean that the two COG-CSAs are different descriptions of the same mind, since, presumably, the two minds are different.

The next step in the argument is the claim that CST is consistent with the nomological possibility of a physical system that simultaneously implements two COG-CSAs. We can assume that the two automata are of the same degree of complexity (if not, we use the number of gates, memory, etc., required for the more complex automaton). I do not claim that any arbitrary system can do this. I also do not claim that any “complex” CSA suffices for a mind. The claim is that if CST is true, then it is nomologically possible to construct such a physical system, rare as it is. Again, I have no proof for this claim. But the constructions of the first section indicate that we can easily construct physical systems out of (physical) gates that are tristable, each of which implements two different (or the same) Boolean functions. Moreover, we can use these gates to construct a physical system that simultaneously implements two CSAs of great complexity; in fact, of any complexity. Take any CSA you wish: We can use the tri-stable gates to build a physical system that implements it. This physical system will simultaneously implement another CSA of complexity of the same degree.

Now, assuming that CST is true, we can use these tri-stable gates to build a physical system BRAIN that implements a COG-CSA, one that is sufficient for mind. This, of course, might be hard in practice, but it seems that it could be done “in principle,” in the sense of nomological possibility. BRAIN simultaneously implements another complex CSA that is of the same complexity of CSA. It consists of tri-stable gates that implement two different or even different runs of the same (like the system S described above) Boolean function. In fact, it seems that it is nomologically possible to simultaneously implement another n different complex CSAs through n-i stable gates. We can complicate the construction of tri-stable gates, at least up to the point that we lose the required stability. We can also think of other, more sophisticated, constructions that have this effect. To be sure, I cannot tell whether the other implemented automata are also COG-CSAs or not (also because we do not know the details of a COG-CSA). I surely have nothing like a proof for the nomological possibility of simultaneously implementing two different COG-CSAs. But given the richness and undemanding nature of these constructions, this option, it seems to me, is something that the friends of CST cannot ignore.

Let us see where we stand. I have argued that if Chalmers’s theory of implementation is correct (as I think it is), then it is nomologically possible to simultaneously implement two different COG-CSAs. Thus, if CST is true (a reductio assumption), then there are nomologically possible scenarios in which a physical system simultaneously possesses two entire minds. The claim is not that BRAIN simultaneously possesses different, even contradictory, psychological and phenomenal properties. The claim is that the very same BRAIN simultaneously possesses two entire minds (perhaps two instances of the same mind) that have (say) different experiences. But one mind (or instance of the same mind) does not have to be aware of the experiences of the other.

As I see it, the friends of CST have two routes here. One is to show that a more constrained notion of implementation is not consistent with these scenarios. I discuss this route in more detail elsewhere (Shagrir 2012), but will say something about it at the end. Another is to embrace the conclusion of a physical system simultaneously possessing two entire minds. Chalmers seems to take this route when saying that “there may even be instances in which a single system implements two independent automata, both of which fall into the class sufficient for the embodiment of a mind. A sufficiently powerful future computer running two complex AI programs simultaneously might do this, for example” (1996: 332). He sees this as no threat to CST. I agree that the multiple-minds scenarios do not logically entail the falsity of CST. But I do think that they make CST less plausible. I will give three reasons for this.

The deluded mind – Two minds often produce different motor commands, e.g., to raise the arm vs. not to raise the arm. But the implementing BRAIN always produces the same physical output (say, proximal motor signals). This, by itself, is no contradiction. We can assume that one mind dictates raising the arm (the output command ‘1’), translated to a 2.5-5 voltcommand to the motor organ. The other mind dictates not to raise the arm (the output command ‘0’), translated to the same 2.5-5 volt-command to the motor organ. The problem is that the physical command results in one of the two; let us say that the result is no-arm-movement. Let us also assume that the same goes for the sensory apparatus, so that the first mind experience a movement (input ‘1’) though there is no movement. This mind is a deluded, brain-in-a-vat-like, entity. It decides to move the arm and even sees it moving, though in fact no movement has occurred. This mind is just spinning in its own mental world. It supervenes on a brain that functions in accordance with the mental states of the other mind.

Let us compare these simultaneous implementation cases to another one. ROBOT is a very sophisticated non-cognitive system that can manage well. ROBOT simultaneously implements two (or more) complex automata, but does not possess minds. Let us say that the two automata produce, as above, different motor syntactic commands (‘1’ vs. ‘0’) through the same physical command (currents of 25-50 volts). How can ROBOT live with itself? The answer in this case is simple: Since we plug (say) the currents of 25-50 volts to no-arm-movement, then the first program, in which 25-50 volts are associated with a move (‘1’) command, is ineffective. ROBOT may simultaneously implement many different programs, but there is only one that makes it move; the others are simply epiphenomenal. If, however, COG-ROBOT is a cognitive system that simultaneously implements two COG-CSAs, then (if CST is true) it possesses two minds, one of which is ineffective and deluded. This is no logical contradiction, but it raises a host of familiar epistemic problems: We might be the epiphenomenal, deluded, mind of some COG-ROBOT.11

The extent of delusion depends upon the pair of minds that can be (if at all) simultaneously implemented. Not every pair enhances the same extent of delusion. There might be cases in which the two minds somehow switch roles or can somehow co-exist, more meaningfully, in the same brain. Two minds, for example, can differ in their phenomenal experience—say, colors —which does not result in any behavioral (physical) difference.12 There are also the cases of split-brain patients, whose corpus callosum connecting the two brain’s hemispheres is severed.13 These patients are capable of performing different mental functions in each hemisphere; for example, each hemisphere maintains an independent focus of attention.14 It sometime even appears as if each hemisphere contains a separate sphere of consciousness in the sense that one is not being aware of the other.15 However, it is also worthwhile to note that the performance of cognitive functions in splitbrain patients is not entirely normal. Moreover, the claim that we have two different entire minds has been challenged too: “Of the dozens of instances recorded over the years, none allowed for a clear-cut claim that each hemisphere has a full sense of self” (Gazzaniga 2005: 657). Our construction suggests that we have two entire minds implemented in the very same physical properties, and connected to the very same sensory and motor organs.

The supervenient mind – Strictly speaking, the scenarios depicted above are consistent with some supervenience of the mental on the physical: Every indiscernible physical system will simultaneously possess these two kinds of mental lives. What is questionable, however, is whether this sort of supervenience is a relation of dependence, between macro and micro properties.16 I find it not too plausible that the very same “micro,” physical, properties simultaneously give rise to two very different “macro” phenomena of the same kind, that function in exactly the same time, place and physical properties. It is odd to think, for example, that the very same molecular motion gives rise to two different temperatures in this room at this particular moment. Splitting the temperature between different objects—same room twice or different rooms—is no better, if the objects are in the same place and time and have the same physical properties. The same goes for minds and brains. Both minds receive and emit just the same physical signals, say voltages of 0-10 volts; moreover, their physical-gate parts also receive and emit just the same physical signals. Even the time it takes to generate the physical signals is (obviously) the same. Yet one mind has the belief that the arm is moving and the other mind the belief that the arm is not. There are, of course, cases in which two or more macro phenomena are inhabited in the same micro-level mechanisms. My body inhabits more than one life, in fact very many lives. A brain region might inhabit more than one cognitive function. Yet in these cases the macro phenomena exhibit some detectable difference in micro properties; we can design experiments by which we detect the difference in micro properties. We can detect, say, some physical signals associated with my life, but not with the life of other organisms that are also part of my body. In contrast, the two minds that supervene on the same brain do not exhibit such a detectable property: They occupy exactly the same space (and time), and exhibit exactly the same micro, electrical, properties. Thus, while one can insist that some sort of psycho-physical supervenience holds, this supervenience diverts from our scientific view about the dependence relations between macro and micro phenomena.

The foundations of mind – Let us assume that further scientific investigation shows that our brains have the ability to simultaneously implement complex automata. The action-potential function might be only bi-stable. The current wisdom is, however, that our cognitive abilities crucially depend on the spiking of the neurons; so perhaps we can implement the CSA in the number of spikes, which are more amenable to multiple implementations. My hunch is that theoreticians will readily admit that our brains (like ROBOT) might simultaneously implement other automata, and that these automata might even be formal, computational, descriptions of (other) minds. Nevertheless, they will be much more hesitant (perhaps for the reasons raised in the supervenient-mind paragraph) to admit that our brain possesses more than one mind. This hesitation is no indication that the possession of a mind is more than the implementation of an automaton. But it is an indication that theoreticians do not take CST as the correct understanding (in the sense of conceptual analysis) of the claim that cognition is a sort of computation. If they did, they must have insisted that brains that simultaneously implement these complex automata simultaneously possess different minds. This is bad news for CST. CST gains much of its support from the claim that it provides adequate foundations for the successful computational approaches in cognitive and brain sciences. If it does not provide the required foundations—if CST and the computational approaches part ways —there are even fewer good reasons to believe in it.

As said, none of these are meant to constitute a knock-down argument against CST. They do not. But I believe that these considerations make CST less plausible.

Now, another route to undermine the brain-possessing-two-minds argument is to put more constraints on the notion of implementation.17 I discuss this issue in more detail elsewhere (Shagrir 2012). Here I want to refer to Chalmers’s statement about constraining the inputs and outputs: “It is generally useful to put restrictions on the way that inputs and outputs to the system map onto inputs and outputs of the FSA” (forthcoming).18 The real question here is how to specify the system’s inputs and outputs. Presumably, an intentional specification is out of the question.19 Another option is a physical (including chemical and biological) specification. We can tie the implementation to specific proximal output, say the current of 2.5-10 volts, or to something more distal, say, physical motor movement. But this move has its problems too (for CST). For one thing, this proposal runs against the idea that computations are medium-independent entities; for they now depend on specific physical inputs and outputs. This idea is central to Chalmers’s characterization of computation as syntactic (see note 19), and as fixing the causal topology of the system. The idea is that while it is important to implement abstract automaton in some physical properties, it is not important which physical properties implement the automaton. For another thing, the proposal has undesired consequences about the typing of computations and minds. Let us say that implementation is tied to the physics of the motor movements. The result is that a robot whose arms are made of metal can never be computationally (hence, mentally) equivalent to a human whose arms are made out of biological material. The reason being that if the physics of inputs and outputs are different then the computational (hence, mental) types are different too.20

The last option, which is more in the spirit of Chalmers, is to characterize the more distal inputs and outputs in syntactic terms. Thus if (say) the output of 2.5-10 volts is plugged to a movement of the arm, and the output of 0-2.5 volts to no-movement, we can say that one automata is implemented and not the other. My reply is that this option helps to exclude the implementations in the case discussed above, but is of no help in the general case. For there is yet another system in which the output of 2.5-5 is plugged to (physical) light movement, and the output of 0-2.5 is plugged to no movement. In this case we can individuate movement (which is just ‘1’) either to high movement or to light-movement-plus-high-movement. In short, there is no principled difference between the syntactic typing of internal and external events. It might help in certain cases, but it does not change the end result about simultaneous implementation. This does not exhaust all the options. But it indicates that finding the adequate constraints on inputs and outputs is no easy task.

10Chalmers refers the reader to the arguments by Armstrong (1968) and Lewis (1972). For criticism see Levin (2009, section 5).  11It would be interesting to see how these cases fare with Chalmers’s argument about the Matrix hypothesis (Chalmers 2005).  12This is not exactly the inverted qualia case. The phenomenal properties are different, but the implemented COG-CSAs are different too (though the inputs/outputs are the same).  13For review see, e.g., Gazzaniga (2005).  14Zaidel (1995).  15Gazzaniga (1972).  16Supervenience does not automatically ensure dependence (see, e.g., Kim 1990, Bennett 2004 and Shagrir 2002).  17Scheutz (2001) offers a thorough criticism of Chalmers’s theory of implementation. His main line is that the more important constraint on implementation, other than being counterfactual supportive, is the grouping of physical states (see also Melnyk 1996; Godfrey-Smith 2009). I believe that my result about simultaneous implementation is compatible with his revised definition of implementation (Shagrir 2012). I agree with Scheutz’s point about grouping, but I suspect that one cannot rule out the cases presented here while keeping a satisfactory characterization of inputs and outputs.  18Piccinini argues that we need to take into account the functional task in which computation is embedded, e.g., on “which external events cause certain internal events” (2008: 220). Piccinini ties these functional properties to certain kind of mechanistic explanation. Godfrey-Smith (2009) distinguishes between a broad and a narrow construal of inputs and outputs.  19Chalmers writes: “It will be noted that nothing in my account of computation and implementation invokes any semantic considerations, such as the representational content of internal states. This is precisely as it should be: computations are specified syntactically, not semantically” (forthcoming).

I have advanced an argument against CST that rests on the idea that a physical system can simultaneously implement a variety of abstract automata. I have argued that if CST is correct then there can be (in the sense of nomological possibility) physical systems that simultaneously implement more than one COG-CSA (or two instances of the same COG-CSA). I have no proof of this result; nor do I think that the result constitutes a knock-down argument against CST. But I have argued that the result makes CST less plausible. It brings with it a host of epistemological problems; it threatens the idea that the mental-on-physical supervenience is a dependence relation, and it challenges the assumption that CST provides conceptual foundations for the computational science of the mind.

20There might be, however, other physical properties that the robot metal arm and the biological human arm share; see Block (1978) for further discussion.