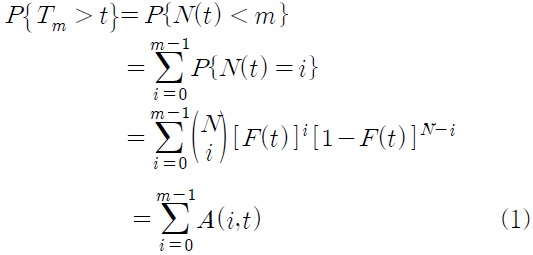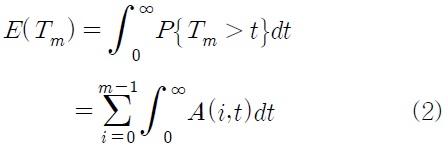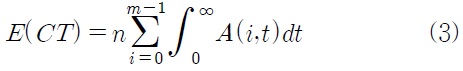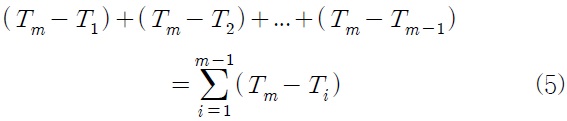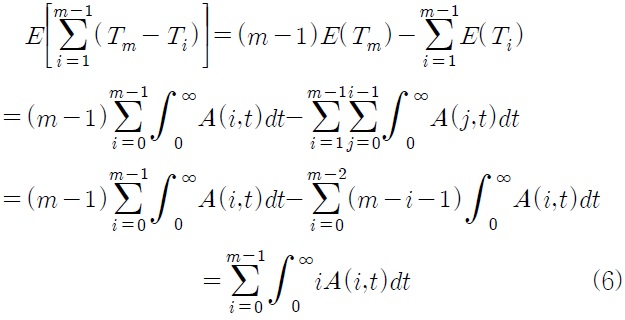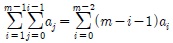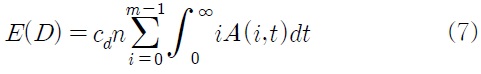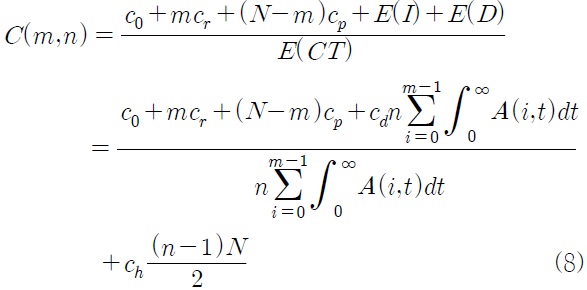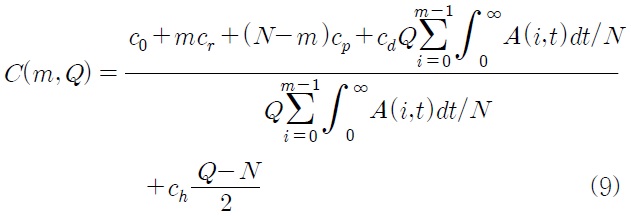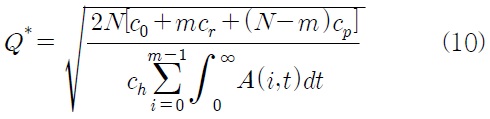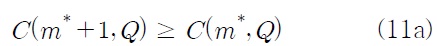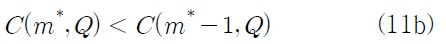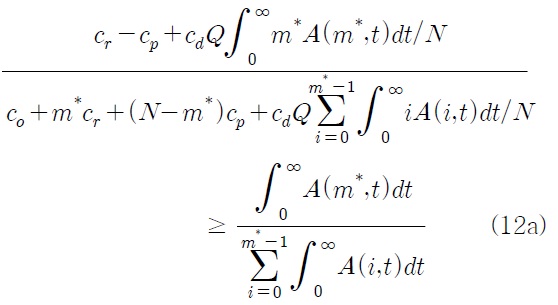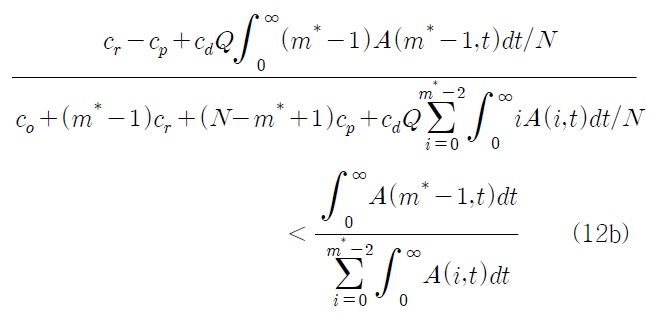In this paper, a jointly optimal group replacement and spare provisioning policy is presented. Most maintenance policies assume that the spare inventory is always available, but in practice the maintenance schedule is affected by the availability of spare inventory. We present a maintenance-inventory model which jointly optimizes the group replacement interval and spare ordering quantity. Group replacement policy is used when a group of units are put in operation simultaneously. The operating fleet is replaced altogether at a predetermined number of units are failed. A sufficient level of spare inventory is carried to perform a number of group replacement. A cost rate expression which considers the group maintenance cost and inventory holding cost is derived and a heuristic method for searching the optimum value of decision variables is suggested. Numerical examples demonstrate the analytical results and the performance of the presented model.
일반적인 보전정책에서는 교체에 필요한 부품이나 장치들이 늘 가용하다고 가정하고 있다. 그러나 만약 교체에 필요한 부품을 보유하고 있지 않다면 현실적으로 보전 업무는 수행될 수 없다. 이러한 이유로 그 동안 보전정책과 예비품 재고정책에 관한 많은 연구가 이루어져 왔다.
보전정책과 예비품 재고정책의 공동 최적화에 관한 연구들은 Van Horenbeek et al.(2013)의 최근 종설논문(review paper)에 잘 정리되어 있다. 보전정책들은 다양한 상황에 맞추어 이에 알맞은 방안들이 개발되어 왔는데, 대표적으로는 수명교체, 일제교체, 최소수리 후 교체 등이며 이들을 재고정책의 여러 방안들과 결합한 공동 최적화 모형들을 정리하여 분류하고 있다.
최근의 이 분야의 연구로는 Lim & Park (2012)을 들 수 있다. 그들은 수명교체와 재고정책을 결합한 운용 방안을 제시하였다. 부품의 교체는 전통적인 수명교체 정책에 의해 수행된다. 부품의 재고는 일정 횟수의 수명교체를 수행할 수 있을 만큼 주문하여 유지한다. 수명교체 관련비용과 재고유지 관련비용의 합을 최소화하는 최적 수명교체주기와 예비품 재고수준을 결정하였다.
동일한 여러 유닛이 동시에 운용되는 경우에는 그룹(group)교체정책이 활용될 수 있다. 그룹교체정책에서는 정기적으로 유닛들이 모두 새 유닛으로 교체되며, 교체 주기 중의 고장은 교체되지 않고 그룹교체 시점까지 기다린다. 물론 이러한 방법은 그룹교체 시점에서 모든 유닛을 한 번에 교체함으로써 보전업무에 소요되는 준비비용(setup cost)을 절약하여 규모의 경제를 얻고자 하는 것이다. 그룹교체정책은 일정 운용시간이 경과하면 그룹교체를 수행하는 소위 T-정책(Okumoto & Elsayed 1983), 일정 개수의 고장이 발생하면 수행하는 m-정책(Assaf & Shanthikumar 1987, Gertsbakh 1984, Wilson & Benmerzouga 1990), 그리고 이 둘을 결합한 (m, T)-정책(Ritchken & Wilson 1990, Popova & Wilson 1999, Yoo & Lee 2001)으로 구분될 수 있다.
일반적으로 부품 수준에 대해 적용하는 일제교체정책과 재고정책의 통합 최적화 문제는 이전에 Acharrya et al.(1986)이나 Yoo et al.(2001) 등에 의해 다수 연구된 바 있으나 그룹교체정책의 경우에는 아직 찾아 볼 수 없다. 여러 유닛이 동시에 운용될 때 적용되는 그룹교체의 경우가 기타의 보전정책에 비해 오히려 재고관리 측면에서 중요하다고 할 수 있다.
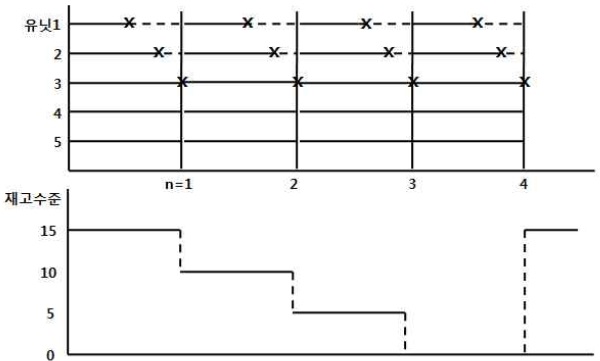
본 연구에서는 그룹교체정책 중 m-정책의 경제적인 수행을 위한 최적 재고 수준을 결정하는 문제를 다루려고 한다. 제안되는 보전-재고정책은 다음과 같다. 동일한 다수의 유닛들이 동시에 운용되며, 일정 개수의 유닛이 고장 나면 그룹교체를 수행한다. 그룹교체 주기 내의 고장은 그룹교체까지 기다린다. 예비품 재고는 일정 횟수의 그룹교체를 수행할 수 있을 만큼 유지한다. 예비품 재고가 없고 동시에 그룹교체가 도래하는 시점에서 조달 주문이 주어지고 재고는 처음의 수준으로 회복되며 그룹교체가 수행된다.
제안되는 보전-재고정책 하에서의 단위 시간당 운용비용이 구해진다. 최적 그룹교체주기와 최적 재고수준을 구하기 위한 방법이 탐색되고, 예시를 통해 본 모형의 성능을 살펴본다.
본 연구에서 제안하는 통합 운용정책은 다음과 같다. 시점 0에서
예비품 재고는 시점 0에서 (
제안된 정책을 이해하기 위한 하나의 예가 다음 <그림 1>에
사용되는 기호들은 다음과 같다. 기타 사용되는 기호들은 필요시에 설명한다.
제안된 보전-재고정책에 따르면 전체적으로
이제 다음의 기호를 정의하자.
그러면 다음의 관계가 성립한다.
따라서 각 유닛의 고장은 서로 독립적이라는 가정 하에서
여기에서 로 간략하여 표시하였다.
하나의 그룹교체에서
이러한 그룹교체가
주기 당 기대비용은 주문비용과 재고유지비용, 그리고 손실비용과 그룹교체비용으로 구성된다. 주문비용과 그룹교체비용은 각각
<그림 1>을 참고하면 주기 당 재고유지비용을 쉽게 구할 수 있다. 입고된
한 번의 그룹교체 동안의 가동중지 시간은 다음과 같다.
식(5)의 기댓값을 구하면 다음과 같이 정리된다.
위의 식(6)을 전개할 때
의 관계식을 사용하였다.
식 (6)은 한 번의 그룹교체 동안의 평균 가동중지 시간이므로 한 주기 당 평균 가동중지 손실비용
식 (4)와 (7)에 주문비용과 그룹교체비용을 더하고 이를 식 (3)의 평균 주기
한편, 예비품의 주문량
비용함수식 (9)는
한편 식 (9)에서
식 (11a)와 (11b)를 전개하여 정리하면 각각 다음과 같은 식을 얻을 수 있다.
따라서 결정변수의 최적 값 (
간단한 수치예제를 이용하여 위에서 도출한 비용함수식으로부터 최적해를 구하고 모형의 성능을 살펴보기로 한다. 각 유닛의 고장은 Weibull 분포를 따른다고 하자. Weibull 분포의 누적분포함수는 F
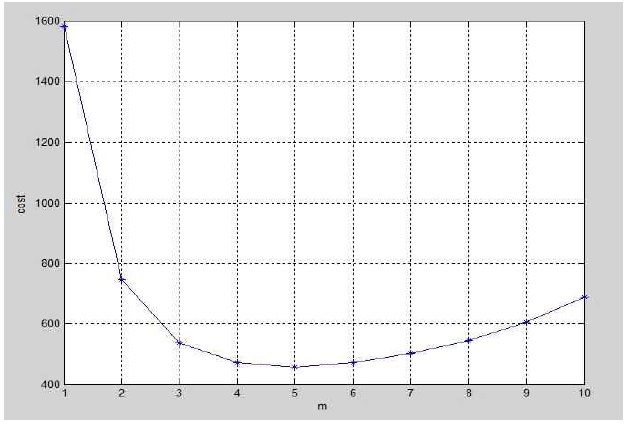
다음의 <그림 2>는
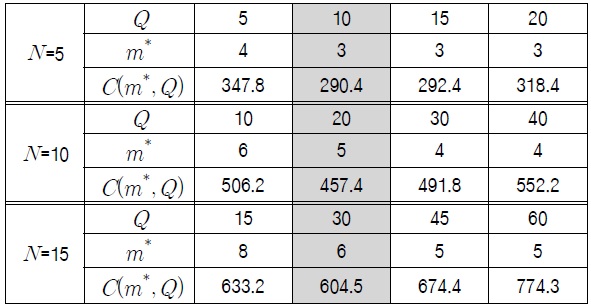
다음의 <표 1>은
[<표 1>] 운용 유닛의 수(N)에 따른 최적해의 변화
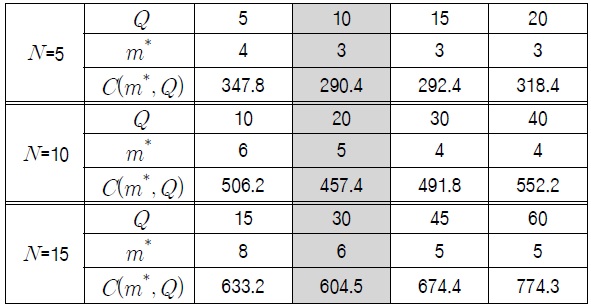
운용 유닛의 수(N)에 따른 최적해의 변화
본 논문에서는 그룹교체와 예비품 재고정책의 공동 최적화문제를 다루었다. 일반적인 보전정책들에서 예비품은 항상 가용하다고 가정하고 있으나 현실적으로는 예비품의 재고 유무가 보전업무의 수행에 직간접적으로 영향을 주므로 이를 고려한 의사결정이 이루어져야 한다.
그룹교체는 여러 동일한 유닛이 동시에 운용될 때 사용되므로 재고수준의 적절한 확보가 다른 보전정책에 비해 오히려 중요하다고 할 수 있다. 본 연구에서는 그룹교체 정책 중 소위 m-정책에 대해 예비품 재고를 동시에 고려하여 최적화하는 방안을 제시하였다. 제안된 정책 하에서의 단위시간 당비용함수식을 도출하고 최적해를 탐색하는 방안을 제시하였으며 수치 예제를 통해 제안된 정책의 성능에 대해 살펴보았다.
본 연구에서는 그룹교체 중 m-정책에 대해서만 모형화와 분석을 시도하였다. 정교하게 개발된 그룹교체정책 중에는 m-정책 이외에 (m,T)-정책과 그 변형들이 있으므로 이에 대해 예비품 재고수준의 공동 최적화를 다루는 연구가 필요할 것이다.