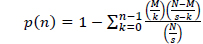Traditionally, several herbs, identified as sovereign, minister, assistant, and envoy have been used simultaneously in oriental medicine. Each herb in a prescription is thought to cooperate or act synergistically with other herbs to alleviate specific symptoms. This tendency toward simultaneous use of cooperative herbs may imply that a group of herbs is more effective in resolving the symptoms than is a single herb. This concept is widely accepted in oriental medicine, but it has not been tested systematically.

Using several herbs simultaneously in one prescription is a major tenet of Traditional East Asian Medicine (TEAM); therefore, it is important to understand systemic features of the relationships among herbs in TEAM prescriptions. A systemic point of view has been applied in modern biology (Chuang et al., 2010), which focuses on the relationships among entities comprising the system of interest. Network analysis, which is one form of systemic analysis, has been applied in biological science (Barabasi et al., 2004) because it captures the holistic properties of systems that consist of the interacting entities where ‘interaction’ depends on context. We applied this method to the pattern of herb use in TEAM to delineate the nature of herb associations in TEAM prescriptions.

The contents of the traditional Korean medicine text (a kind of TEAM) called Inje-ji (Seo, 1983) were examined by licensed doctors and scholars of traditional Korean medicine at the Imwon Institute for the Classics, Republic of Korea. The source text Inje-ji consists of more than a million classical Chinese characters and contains 5,376 herb cocktail prescription–symptom sets. The Inje-ji was written by Seo Yugu (1764-1845), a pragmatic Confucian scholar of the late Joseon dynasty. Recently, all the contents of Inje-ji were transcribed using a consistent punctuation pattern to allow for statistical analysis.

In the source text Inje-ji, each cocktail prescription contains a list of ‘herbs’ and ‘symptoms’ that the prescription is expected to treat. Therefore, all the vocabularies or terms indicating ‘herbs’ and ‘symptoms’ were extracted from the 5,376 cocktail prescriptions by text mining and then refined manually several times by professional scholars of traditional Korean medicine.

Herb-pairing specificity was calculated as the Fisher’s exact p-value for the number of prescriptions containing both herbs against those containing each herb alone.

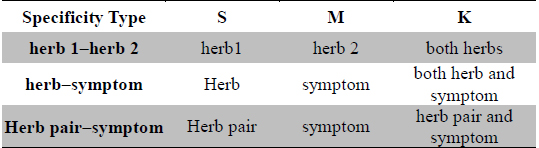
[Table 1.] Meaning of variables used in Formula 1

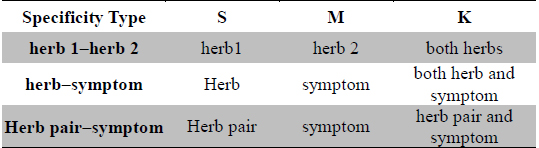
Meaning of variables used in Formula 1

In the herb-pairing network, a node represents a single herb, and two herbs are connected in cases when the pairing specificity of the two herbs is statistically significant (FDR < 0.01) and the two herbs are simultaneously used in more than four TEAM prescriptions. Once the herb-pairing network was constructed, the network was considered as an unweighted network. Visualization of the herb-pairing network was performed using Cytoscape version 2.8.1 (Shannon et al., 2003), and node properties including the clustering coefficient, betweenness centrality, and others were calculated in an undirected network mode using the Network Analyzer plug-in (Assenov et al., 2008) release version 2.7. Symptom-specific herb-pairing sub-networks were found by the MCODE (Bader et al., 2003) plug-in of Cytoscape software.

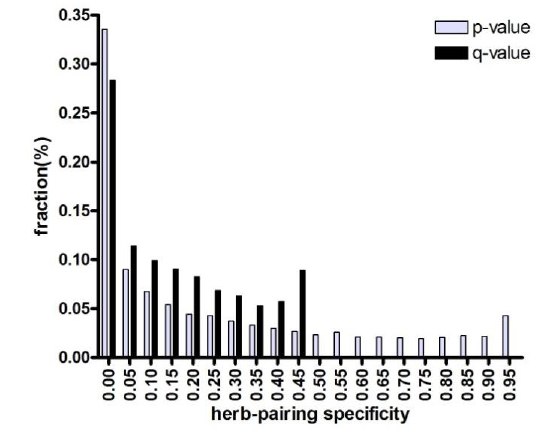
We examined the statistical significance of cooperative relationships (herb pairings) using Fisher’s exact test (Fig. 1) for all herbs presented in the text source. More than 28% of herb cooperation were found to be significant (false-discovery rate (FDR) < 0.05). This result indicates that each herb of the herb pair was specifically used with the other herbs in TEAM prescriptions. Furthermore, TEAM proposes that some herbs should not be used with each other (incompatible herb pairs, xiangfan) due to conflicts. This concept was manifested as an increase in herb pairs with large FDR (> = 0.45), which is attributed to the low numbers of prescriptions containing the herb pairing. These results collectively suggest that the use of two herbs simultaneously in a same prescription has generally been either preferred or deliberately avoided.

[Fig. 1.] Significance of herb-pairing specificity. More than 28% of the herb pairings were symptom specific. Two herbs were regarded as specific herb pairs when prescriptions containing both of the herbs was significant in terms of those prescriptions containing each of the herbs alone based on Fisher’s exact test. The y-axis indicates the proportion of all herb pairs with the specificity indicated on the x-axis.

We generated the herb-pairing network (Fig. 2, force-directed layout by Cytoscape). In the network, a node represents a herb, and an edge indicates that two connected herbs are specifically paired by Formula 1 with FDR < 0.01. The herb-pairing network has a total of 256 herbs and 1659 edges. It is well known that various networks with different types are scale-free, i.e., follow a power-law, in various fields (Lima-Mendez et al., 2009). The herb-pairing network is also a scale-free network, with 0.927 as the gamma parameter. The herb-pairing network has a larger clustering coefficient (0.374) compared with a random network (0.202) with the same degree of distribution. 'Hub' herbs of the network were identified as Glycyrrhiza uralensis (甘草, 77 herbs with specific pairings), followed by Angelica sinensis (當歸, 72), Saposhnikovia divaricata (防風, 61), and Ligusticum chuanxiong (川芎, 59).

[Fig. 2.] Herb-pairing network used in Traditional East Asian medicine text Inje-ji. Each node represents a herb, and herb pairs with FDR < 0.01 are connected. The node color indicates betweenness centrality of the node, and node size is proportional to the number of neighbor nodes connected to the node.

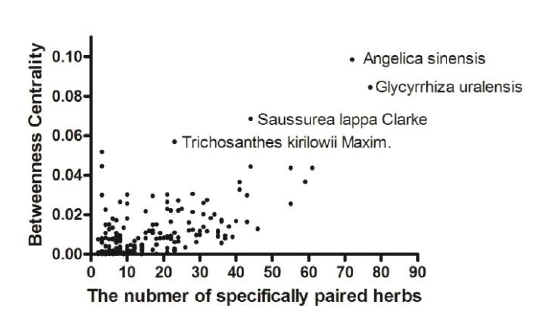
The fact that a herb is specifically paired with many other herbs does not necessarily indicate the importance of the specific herb. To evaluate the importance of a herb in the herb-pairing network, we assessed the correlation of the herb–symptom specificity and the properties of the nodes in the herb-pairing network using the Network Analysis plug-in in Cytoscape (Assenov et al., 2008). Herb–symptom specificity was calculated using Formula 1. The betweenness centrality (BC) of a node, which reflects the number of the shortest paths that traverse the node divided by all shortest paths in the network, and stress, which indicates the number of the shortest paths that transverse the node, are well-known important node properties in a network (Newman et al., 2001). Importance of stress and BC were assessed in terms of herb–symptom specificity. The correlation between herb–symptom specificity and stress was 0.3921, and that for BC was 0.2679 (see 3.4 for a discussion of herb–symptom specificity). We checked the degree of nodes, which is the number of nodes connected to the node and the BC of the nodes simultaneously because the degree is the most profound property of the nodes in the network (Fig. 3). Trichosanthes kirilowii Maxim has a relatively large BC compared with other herbs having a similar degree. This result indicates that Trichosanthes kirilowii Maxim is more specific to symptoms compared with other herbs having a similar number of specifically paired herbs.

[Fig. 3.] Relationship between betweenness centrality and the number of paired herbs. Each node indicates a herb, and the x-axis shows the number of herbs paired with the herbs. y-axis shows the betweenness centrality of the herb in the herb-pairing network.

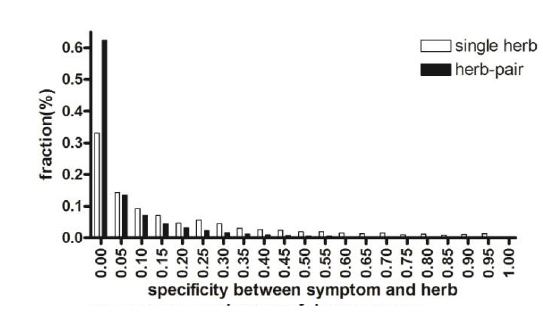
The specificity of herb pairing observed in Fig. 1 is based on the idea that pairs of herbs are more effective at alleviating a symptom than is a single herb alone because each herb is paired with a specific herb counterpart to exert synergistic or cooperative effects. To test this notion, we compared the association specificity of symptoms with a single herb and with herb pairs (Fig. 4). We considered herbs to be associated with a symptom if the herbs were used in cocktail prescriptions to treat a symptom, as described in the Materials and Methods. As shown in Fig. 4, herb pairs were more specifically associated with symptoms than were single herbs alone (FDR < 0.05).

[Fig. 4.] Distribution of specificities between the symptoms and the single herb or herb pair. Herb pairs are more specific to symptoms than are single herbs. The x-axis is specificity between the symptom and the herb pair or single herb, as reflected by the Fisher’s exact p-value. More than 60% of the herb pairs were significantly specific to symptoms, but only about 30% of single herbs were specific to the symptom.

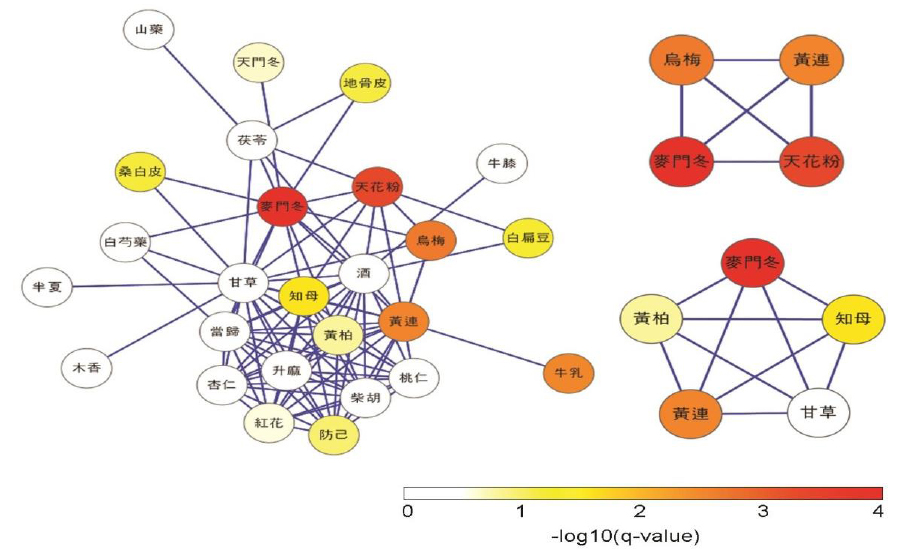
The herb-pairing network can be used to assess which herbs are employed for a particular symptom. As a representative example, we created a herb-pairing network for diabetes mellitus (DM), shown in Fig. 4. Node color indicates single herb specificity for diabetes as described in the Methods. In this network, Glycyrrhiza uralensis had the largest BC but nonsignificant specificity with DM. However, Ophiopogon japonicus, Coptis chinensis, and Trichosanthes kirilowii Maxim were found to be important in the DM-specific herb-pairing network based on BC, which is concordant to herb–symptom specificity of the herbs.

Finding a combination of herbs that is thought to be effective in resolving a particular symptom is difficult because of the vast number of possible herb combinations. We attempted to address this problem by identifying a cocktail of herbs that satisfied the following conditions: 1) the average of the specificities of the herbs with respect to the symptom was significant, and 2) all possible herb pairs from the cocktail were specific to the symptom according to the symptom-specific herb-pairing network. Two representative cocktails are shown in Fig. 5, which suggests these can be core cocktails from which various TEAM prescriptions for DM would be developed.

[Fig. 5.] Herb-pairing network for diabetes mellitus. A sub-network composed of herbs used for diabetes mellitus (DM) was extracted from the herb-pairing network. Two representative strongly connected sub-networks were also identified for DM. The color of the node indicates specificity of the node to DM presented by the q-value of -log10.

We performed systemic analysis of the herb-pairing properties documented in the traditional Korean medicine text Inje-ji, which contains more than 5000 prescriptions. We assessed the entire text, which makes this study different from other studies that used objectively selected prescriptions from various texts. Our results show that more than a quarter of the total herb pairs were associated with specific herb pairings. Herbs that should not be paired were also observed. Moreover, herb pairs were more specific to the symptoms than was a single herb alone, which revealed synergistic/cooperative principles embedded in TEAM prescriptions. As a representative example of the potential of our approach, the herb-pairing network for DM was provided. To the best of our knowledge, this is the first report demonstrating that TEAM herb pairing is not random but specific and, more importantly, that herb pairs are more specific to the symptoms than is a single herb. These results reveal synergistic and/or cooperative principles embedded in TEAM that has not previously been tested statistically.

One of the major tenets of TEAM is that several herbs should be used simultaneously for a symptom. These combined herbs are known as sovereign, minister, assistant, and envoy. This implies that a group of herbs is more effective for treating a certain symptom than is a single herb, which is shown indirectly in Fig. 4. By considering that diseases stem from the malfunction of a series of key pathways, TEAM prescriptions are thought to resolve symptoms by operating on several factors simultaneously.

The widespread existence of cooperative herb pairs is thought to reflect the historical evolution of TEAM. Preferential attachment is known to be one of the major properties of a scale-free network. The herb-pairing network shown in Fig. 3 is scale-free, which implies preferential use of previously used herbs. If herb pairs used in TEAM were paired randomly, then the distribution of p-values for the pairings (which can be calculated by Fisher’s exact test or chi-square test) would be flat and have no significant q-value. The fact that most herb pairs are significantly associated with symptoms, whereas single herbs are not, shows that doctors or therapists using TEAM have selected the herb pairs based on their clinical experience over a long period of time. In the case of incompatible herb pairs, the pairing would have been excluded from a probable prescription pool because of side effects or ineffectiveness, which could be caused by interactions of the herbs, which may generate toxic effects or counteract the effects of other herbs.

The current knowledge embedded in TEAM is a reservoir of remedies that have been selected over the course of more than 2000 years in Asia, although the mechanisms of their action were unknown. Although this approach lacks sufficient detail for scientific explanation, the composition of TEAM was found to be statistically significant in this study. Attempts to identify chemical compounds with medicinal effects from TEAM continues, but still with few representative examples, such as artemisinin and arsenic trioxide. Therefore, we suggest that the combination of a group of chemical compounds from several kinds of herbs, rather than a single ingredient, endows the prescriptions with therapeutic effects. Furthermore system medicine and network theory will contribute to the essential clarification and application of medicinal information embedded in TEAM.

By systemic analysis of a whole traditional medicine text, we have shown that combinations of herbs used in TEAM prescriptions are not random; instead, specific herb pairings are prevalent. Synergistic/cooperative properties of herb pairing were shown by the superior specificity of symptoms with herb pairs compared with treatments involving a single herb. Therefore, a symptom-specific herb-pairing network can be used to identify herb combinations that have promising therapeutic effects with respect to particular symptoms. This suggests that not a single compound, but a set of compounds provides the therapeutic effects observed in TEAM and that an attempt to find a new drug candidate from TEAM would have an increased chance of success by focusing on a combination of compounds.