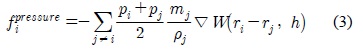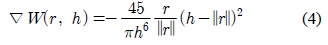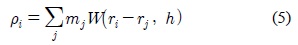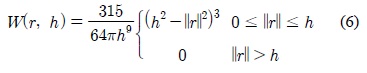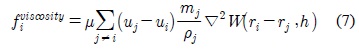In this paper, we propose a GPU-based interactive and plausible visualization method for the silt and landslide simulation results computed with SPH. By empirical experiments, we verify that our GPU-accelerated screen space mesh method can be effectively used for visualizing the landslide disaster simulation. The method proposed in this paper make it possible to overcome the limitation of previous simulations where the experience obtained by trials and errors plays the most important roles. Because the realtime visualization enables interactive observation of simulation results and efficient data assimilation, the accuracy of the simulation can be significantly improved in an efficient way.
최근 다양한 물리기반의 컴퓨터 시뮬레이션 기술을 활용하여 위험 예측을 위한 가상 재해 시뮬레이션 연구가 활발히 진행되고 있다[1-3]. 그 중에서도 시뮬레이션에 의한 대규모 데이터를 효율적이고 직관적으로 표현하기 위한 데이터 시각화 기술은 필요 불가결한 요소이다. 특히 시뮬레이션 실행 도중 경과를 상호작용을 통해 다양한 각도에서 관찰할 수 있도록 하는 실시간 처리는 의사결정 인터페이스로서 매우 중요하다.
일반적으로 복잡한 형상변형을 가지고 있는 유체 시뮬레이션은 주로 나이비에 스토크스방정식을 기반으로 하는 격자법과 입자법이 가장 많이 사용되고 있다. 격자법은 공간을 고정된 격자로 나누어 그 위치에서의 물리량을 시간 마다 계산하는 방법으로 비교적 부드러운 유체의 표면 움직임을 잘 표현할 수 있지만 난류와 같이 유체 표면의 결합과 분열이 반복되면서 복잡하고 무질서한 움직임을 표현하는데 있어서는 어려움이 있고 를 표현하기 위해서 조밀하게 격자를 구성하여 시뮬레이션을 해야 하기 때문에 많은 계산비용이 소모된다. 한편 입자법은 입자를 계산 요소로 고려하여 입자를 이동시키면서 물리량을 계산해 나가는 방법이다. 주로 SPH[4]방식과 MPS[5]방식이 많이 사용되고 있다. 이 방법은 격자를 생성할 필요가 없기 때문에 격자가 꼬이는 등의 위상관계를 고려할 필요가 없어 수치안정성과 난류와 같은 복잡한 유체 유동 표현에 장점을 가지고 있다. 또한 격자법에 비해 계산비용이 적고 병렬성이 높아 실시간 시뮬레이션을 수행하는 적합하다. 하지만 입자법은 입자의 움직임에 대한 위치정보만을 가지고 있어 유체의 유동 표면을 사실적으로 가시화하기 위해서는 유체 표면을 생성하여 렌더링 할 필요가 있다.
이에 본 논문에서는 SPH에 의한 토사 유체 유동 시뮬레이션 결과를 GPU 병렬처리를 통해 사실적이고 인터랙티브가 가능한 실시간 가시화 방법을 제안한다. 또한 본 논문에서는 실험을 통해 제안한 실시간 가시화 방법을 검증하여 그 타당성을 논하고자 한다.
본 논문의 구성은 다음과 같다. 제2장에서는 대규모 유체 입자 시뮬레이션에 대한 시각화 처리의 관련연구에 관해서 언급한다. 제3장에서는 SPH 수치 시뮬레이션 방법과 가속화를 위한 병렬화 방법을 소개한다. 제4장에서는 대규모 입자 데이터의 실시간 유체 렌더링 방법에 대해 소개한다. 제 5 장에서는 본 논문에서 제안한 실시간 입자 유체 렌더링을 실험을 통해 검증하고, 마지막으로 6장에서는 결론과 함께 향후의 문제를 다루고자 한다.
복잡한 형상이나 큰 변형을 일으키는 토사, 물, 연기 등의 유체 현상을 시뮬레이션과 컴퓨터 그래픽을 통해 현실적으로 표현하기 위한 다양한 시각화 방법이 제안되고 있다[6-9]. 먼저 유체 시뮬레이션에서 유체를 기술하는 방법으로는 크게 격자법으로 대표되는 오일러 기술방법과 입자법으로 대표되는 라그랑주 기술방법이 있다.
Stam[10]은 세미-라그랑주 이류법(semi lagrangian advection scheme)을 통해 격자법에서 유체의 움직임을 안정적으로 푸는 방법을 제안하여 컴퓨터 그래픽 분야에서 폭넓게 사용되고 있다. 하지만 이 방법은 이류항에 의한 수치 확산이라는 잠재적인 문제를 안고 있고 또한 난류에너지의 소실에 의해 난류장을 유지하는 것이 어렵다. 이 방법을 개선하기 위해서 고차 보간법을 이류에 적용하는 방법이 제안되었다[11,12].
한편 입자법은 매우 작은 유체 덩어리(입자)에 주목하여 이를 추적하면서 이에 대한 물리량을 변시키는 방법이다. 이 방법은 유체를 입자들의 집합으로 간주하기 때문에 입자수가 변화 없으면 질량보존법칙을 만족하기 때문에 격자법과 같이 연속식을 풀 필요 없고 계산 비용이 적다. 따라서 입자법이 격자법보다는 인터랙티브가 가능한 실시간 유체 시뮬레이션에 적합하다. 그러나 이 방법은 시뮬레이션 결과를 바로 렌더링 할 경우 구형 형태의 입자로 표현하기 때문에 사실성이 약하다. 따라서 렌더링에서 사실성을 표현하는데 중요시되는 빛의 반사, 굴절을 표현하기 위해서는 입자군으로부터 유체 표면을 생성할 필요가 있다[19-21].
이에 Muller 등 [13]은 SPH 시뮬레이션을 실시해, 매칭큐브(Marching Cubes) 법[14]에 의해 액체 표면을 생성하여 대화형 유체 애니메이션을 가능하게 했다. 또한 Yu 등은 매칭 큐브에 사용 음함수를 계산할 때 이방성 커널을 사용하여 매끄러운 표면을 생성했다[15]. 그러나 커널의 방향을 결정하기 위해 주성분 분석해야하기 때문에 실시간 유체 렌더링에는 적합하지 않다. 한편 Van 등은 표면 메쉬 생성을 하지 않고 가시영역의 표면 부분만을 렌더링 방법을 제안했다[16]. 그러나 이 방법은 입자를 구형으로 표현해서 렌더링하기 때문에 근접거리에서는 표면이 구형 요철과 같이 표현되는 단점이 있다. 매칭규브법을 사용하여 삼각형 메쉬를 추출하는 경우는 3D 공간을 3D 격자 구조로 분할하여 각 셀에서 메쉬를 생성하는 것이 일반적이다. 이에 대해 Muller 등은 2D 스크린 공간에서 유체 표면 메쉬를 생성하는 스크린 공간 메쉬(Screen Space Meshes, 이하 SSM)방법을 제안하였다[17]. 이 방법은 3D 공간에서 입자를 2D 화면 공간에 투영하여 생성된 깊이 맵에서 2D 메쉬를 생성하고 이를 3D 공간에 역투영한 것 중 은면 제거와 같이 가시영역에 있는 메쉬만를 생성한다. 또한 깊이맵에 스무딩 필터링하여 메타볼과 같은 렌더링을 얻을 수 있다. 이는 기존의 3D 매칭규브 방법의 계산 비용
이에 본 연구에서도 SSM을 이용하여 토사 재해 시뮬레이션 등에 적용할 수 있는 유체 시뮬레이션의 실시간 가시화 방법을 제안하여 적용하였다.
기존의 다양한 재해 예측 시뮬레이션에서는 주로 FEM(Finite Element Method)을 이용한 여러 가지 해석 Solver들이 적용되어왔다. 그러나 FEM으로 하는 격자법은 재해 예측 시뮬레이션과 같은 대규모 데이터를 병렬처리을 통해 실시간계산에는 부적합한 측면이 있다. 이에 본 연구에서는 실시간 병렬처리를 통해서 토사 재해의 유동해석을 하기 위해 SPH(Smoothed Particle hydrodynamics)기법을 도입하여, 유체의 유동성에 대한 해석을 통하여, 발생 할 수 있는 재해를 미리 예측 하는 시뮬레이션을 개발하였다.
3.1. SPH기반 토사 재해 예측 3D 시뮬레이션 가시화 시스템 플레임웍
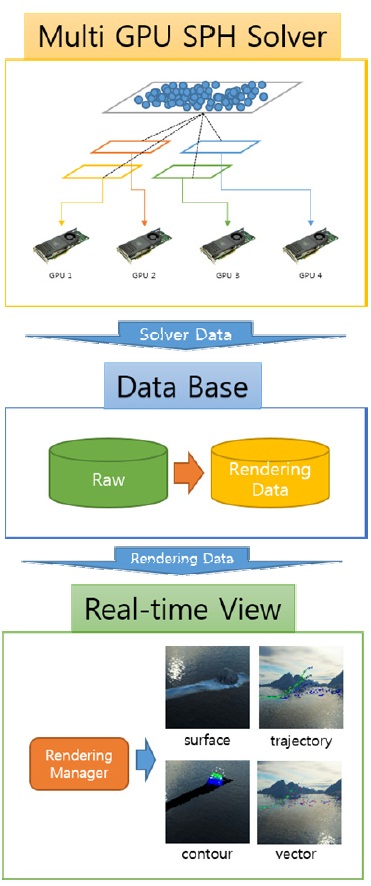
3D 시뮬레이션 가시화 시스템은 크게 유체의 유동해석을 위한 SPH Solver, 시뮬레이션 결과 데이터 입출력DB 그리고 시뮬레이션 가시화 부분으로 3개의 부분으로 나누어진다. 본 연구에서 개발한 가시화 시스템은 [그림 1]과 같이 SPH기반의 토사 재해 시뮬레이션과 이에 대한 결과를 DB에 저장하고 이를 실시간 가시화처리를 하는 시스템으로 구성되어 있다.
SPH (Smoothed-Particle Hydrodynamics)는 입자법 기반의 유체의 흐름을 시뮬레이션 하는 기법 중 하나로 천체 물리학 문제의 해결을 위해 1977년 Gingold와 Monaghan, Lucy[18]에 의해 제안되었다. 현재 SPH 방식은 천체 물리학, 탄도, 산학, 해양학 등의 많은 연구분야에서 사용되고 있으며 Mesh를 사용하지 않는 라그랑주 방식으로, 그 해는 밀도, 점성, 압력 등의 항에 영향을 받는다.
SPH는 기존의 격자법 보다는 다음과 같은 이점으로 인해 최근에 유체의 움직임을 모델링 하는데 많이 사용되고 있다. 첫째 SPH는 각각의 입자가 질량을 포함하고 있기 때문에 별도의 계산 없이도 질량 보존이 보장되며, 둘째로 SPH는 선형 시스템을 해석하지 않고 이웃한 입자의 거리 가중치에 따라 압력을 계산한다. 마지막으로 유체의 경계를 찾기 어려운 그리드 기반의 기술과는 달리 입자 기반의 SPH는 유체의 경계를 쉽게 찾을 수 있다.
SPH는 Navier-Stokes 방정식을 지배방정식으로 이용한다. Navier-Stokes 방정식은 [식1]로 표현된다.
[식 1]에서 우항의 각 요소들은 각각 압력(-∇
[식 2]의 압력 은 [식 3]으로 표현된다.
[식 3]에서
커널 함수 ∇
밀도 함수
[식 5]에서
[식 2]의 점성 은 [식 7]로 표현 된다.
[식 7]에서 커널 함수 ∇2
[식 2]의 외력 은 중력이나 충돌과 같은 경계조건, 또는 사용자가 임의로 가한 힘 등을 나타내며 SPH를 사용하지 않고 입자에 직접 가해지는 힘을 말한다.
SPH 알고리즘 특성상 많은 연산을 필요로 한다. 하지만 앞서 설명한 SPH의 각 함수의 특징을 보면 각 입자별로 독립된 계산이 가능하기 때문에 병렬처리에 적합하다. 이에 본 논문에서는 NVIDIA사의 CUDA 병렬연산을 통해 SPH 알고리즘에 의한 유체의 움직임을 실시간으로 계산하였다.
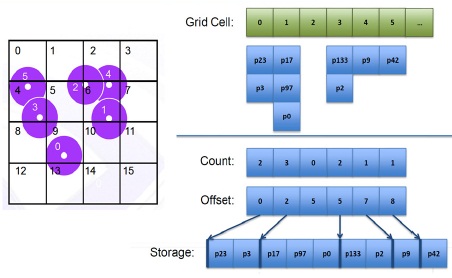
SPH의 각 함수를 병렬로 계산하기 위해서는 기본적으로 인접한 입자들의 정보가 필요 하다. 하지만 인접한 입자들의 정보는 선형적으로 탐색할 수밖에 없는 문제점이 존재 한다. 이에 본 논문에서는 [그림 2]와 같이 시뮬레이션 공간을 일정한 격자 영역으로 구분한 후 각 영역에 속한 입자들의 정보를 스트림구조로 저장하고 인접 영역의 정보가 요구될 때 사용되도록 하여 탐색을 고속화 하였다.
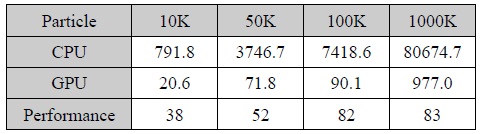
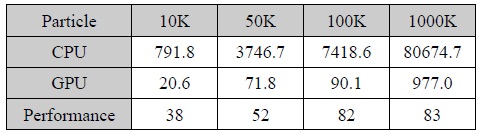
[표 1]은 단일 CPU 계산과 CUDA 병렬 계산에 대한 성능 평가를 나타내고 있다. 본 연구에서는 [표 1]과 같이 1000만개 입자 계산의 경우 단일 CPU에 비해 약 80배 이상의 성능 향상이 있는 것을 알 수 있었다.
[표 1.] SPH 유체 시뮬레이션에 대한 CPU(intel i7) vs CUDA (M2090) 성능 평가(ms/step)
SPH 유체 시뮬레이션에 대한 CPU(intel i7) vs CUDA (M2090) 성능 평가(ms/step)
토사 재해를 예측하기 위한 유체 시뮬레이션에서는 대규모의 입자를 필요로 한다. SPH에 의한 유체 시뮬레이션의 결과 데이터는 입자들의 위치, 속도, 밀도 등의 수치 정보이다. 이러한 입자들의 수치 정보만으로는 토사 재해 예측 분석에는 많은 어려움이 존재 한다. 이에 본 장에서는 GPU를 활용한 실시간 유체 렌더링 방법에 관해서 설명하고자 한다.
유체를 시뮬레이션 하는 가장 큰 이유는 유체 입자들의 흐름을 분석하기 위해서 이다. 입자들은 순간적인 속도, 밀도 등과, 시간 흐름에 따른 유체 입자들의 위치정보 등을 가지고 있다. 이러한 정보를 실시간으로 가시화 하는 것은 정보 분석에 매우 유용하다.
본 논문에서는 유체의 흐름 정보를 가시화 하는 방법으로 크게 두 가지를 사용하였다. 일정 영역의 입자들의 정보를 평균적으로 분석할 수 있는 벡터 표현과, 각 입자별로 움직임을 분석할 수 있는 궤적 표현이다.
4.1.1. 벡터 표현
벡터 표현은 입자들의 순간적인 정보를 가시화 하는 것으로 유체가 흐르는 각 영역의 평균 정보를 나타낸다. 벡터 표현은 순간적으로 발생할 수 있는 유체의 쏠림 현상 등을 관찰 하는데 적합하다. 이러한 벡터 표현을 실시간을 가시화하기 위해서는 많은 수의 입자들을 각 영역별로 구분하는 작업이 필요하다.
입자들을 영역별로 구분하는 가장 단순한 방법은 2차원 그리드를 사용하는 것이다. 일정한 크기로 구분한 그리드 자신에 영역에 속한 입자들의 정보를 가지고 있다. 각 그리드는 자신에게 속한 입자들의 정보를 이용하여 평균적인 정보를 구한다.
[그림 3]는 각 그리드 별로 구분된 공간상에 입자들의 정보를 가시화 한 것이다. 입자들의 평균 방향을 화살표로, 입자들의 속도의 평균을 화살표의 색으로 가시화 했다.
4.1.2. 궤적 표현
궤적 표현은 입자들의 시간에 따른 흐름을 판단하기 위해서 필요한 정보이다. 입자들은 시간이 흐름에 따라 각 시간별로 위치 정보를 가지고 있다. 이러한 위치 정보를 이용하여 궤적을 표현 할 수 있다. 궤적 정보는 유체의 병목구간을 판단하는데 적합하며, 유체의 흐름이 정체 되어 있는 병목 구간은 토사 재해가 나타날 수 있는 구간으로 이러한 부분을 실시간으로 가시화 하는 것은 중요한 부분이다.
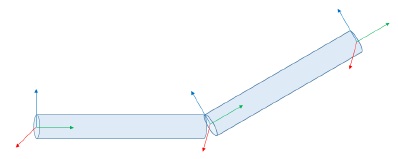
일반적으로 궤적을 표현하기 위해서는 [그림 4]와 같이 실린더 형태의 메쉬를 사용하게 된다. 입자의 위치정보를 이용하여 3차원 공간상에서 실시간으로 실린더를 생성하기 위해서는 [그림 5]와 같이 각 위치에 있는 입자의 3차원 축 정보가 필요하다.
하지만 SPH기반 유체 시뮬레이션에서 입자는 3차원 축 정보를 가지고 있지 않다. 일반적으로 3차원 축 정보가 없이는 메쉬를 제작 할 수 없다. 본 논문에서는 실린더 형태의 메쉬를 구성하기 위해서 입자의 위치에 3차원 축을 근사하는 방식을 사용한다.
[그림 6]는 시간에 흐름에 따른 입자들의 정보를 가시화 한 것이다. 입자의 위치 정보를 실린더 형태의 메쉬를 이용하여 가시화 했다. 또한 입자들의 순간적이 속도 정보를 실린더의 색으로 나타냈다.
유체의 표면 표현은 복잡한 형상을 가지는 유체의 유동을 사실적이고 직관적으로 판단하는데 에 매우 중요한 가시화 기술이다.
SPH를 이용한 유체 시뮬레이션은 단순히 구 형태의 정보만을 가지고 있어 움직임을 직관적으로 판단하기 에는 어려움이 있다. 본 논문에서는 유체의 움직임을 직관적으로 표현하기 위해 Screen Space Meshes(SSM)와 Screen Space Fluid(SSF) 기법을 이용하여 가시화하였다.
4.2.1. Screen Space Meshes
SPH기반의 유체 시뮬레이션은 입자를 이용하기 때문에 3D 공간상에 Mesh를 생성하기 어렵다. 본 논문에서는 입자 정보만을 이용하여 3D 공간상에 Mesh를 생성할 수 있는 SSM기법을 사용하였다. 이 기법은 Muller[17]가 처음 제안한 방식으로 기존의 3D Mesh 제작 방식인 매칭 큐브방식의 문제점인 속도 문제를 해결한 방식이다.
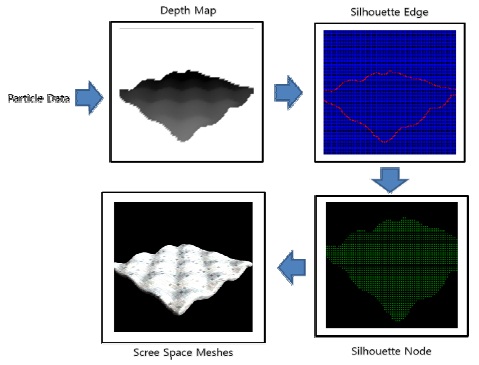
[그림 7]는 SSM 기법의 알고리즘을 도식화 한 것이다. SSM는 입자의 위치 정보를 이용하여 2D Screen 좌표계에 깊이 맵를 제작한다. 이렇게 만들어진 깊이 맵을 이용하여 2D Screen 좌표계에 메쉬를 구성할 정점을 생성한다. 2D 공간상에 구성된 Mesh정보를 다시 3D공간상으로 복원함으로써 3D 공간상의 메쉬를 생성한다.
4.2.2. Screen Space Fluid
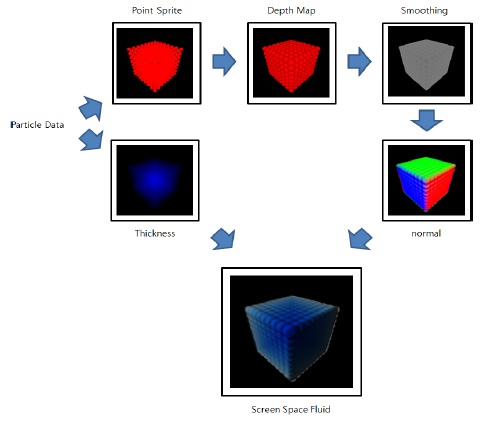
SSF방식은 Van Der Laan[16]가 처음 제안한 기법으로 SSM방식과 비슷하게 입자의 위치 정보와 크기 정보를 이용하여 물의 표면을 표현하는 기법이다. 하지만 SSM과는 다르게 Mesh를 생성하지 않는다. 이 기법은 SSM기법 보다 좀 더 그럴듯한 물의 표면을 생성하기에 적합한 방식으로 모든 계산이 Shader를 이용하여 처리 되어 실시간 유체 표면 처리에 적합하다.
형태로 만든다(Point Sprite). 이와 동시에 위치 정보 를 이용하여 유체의 깊이 정보(Thickness)를 만든다. 구형 태로 만들어진 입자 정보를 이용하여 깊이지도(Depth Map)을 제작하고 제작된 깊이 정보를 평탄화 작업(Smoothing)을 통해 평평한 유체의 표면을 제작한 다. 다시 평탄화된 정보를 이용하여 유체의 표면 벡터지도(Normal Map)를 제작한다. 최종적으로 표면 벡터맵과 깊이 정보 맵을 이용하여 유체의 표면을 가시화한다.
SPH를 이용한 토사 재해 예측 시뮬레이션은 많은 양의 수치 정보를 생성한다. 이러한 수치 정보를 실시간을 가시화 하는 기술은 매우 중요하다. 본 논문에서는 SPH기반의 유체 시뮬레이션 데이터를 실시간으로 가시화 하는 기술을 제안하였다. 실험은 한계령의 모델링 데이터에 SPH 입자 30만개를 이용하여 실험하였다.
[그림 9]는 SPH 기반의 유체 시뮬레이션 결과로 나온 수치 정보를 이용하여 입자의 위치를 시간 흐름에 따라 궤적으로 표현한 것이다.
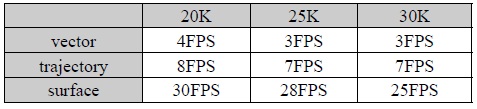
[그림 10]는 순간적인 입자의 위치 정보를 구역별로 평균한 정보를 벡터를 이용하여 가시화 한 결과이다. [그림 11, 12]는 입자 정보를 이용하여 실시간으로 유체를 가시화 한 결과이다. [표 2]는 입자 30만개를 이용하여 벡터표현, 궤적 표현, 표면 현을 실험한 결과이다.
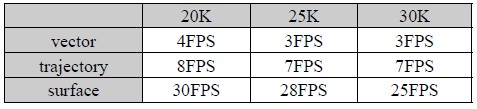
SPH 유체 시뮬레이션 가시화 결과
본 논문에서는 SPH에 의한 토사 유체 유동 시뮬레이션 결과를 GPU 가속화 처리를 통해 사실적이고 인터랙티브가 가능한 실시간 가시화 방법을 제안하였다. 지금까지 토사 재해 시뮬레이션과 같은 대규모 유체 시뮬레이션의 결과 가시화 방법은 주로 화면 캡처를 통한 동영상 재상수준에 지나지 않았다. 이에 반해 본 논문에서 제안한 방법은 복잡한 형상이나 큰 변형을 일으키는 유체 시뮬레이션의 결과를 실시간으로 인터랙티브하게 다양한 측면 관찰할 수 있어 가시화 분석을 통한 결과 활용기술로서 매우 중요하다고 할 수 있다. 또한 제안한 방법은 다른 입자법 시뮬레이션에 가시화하는 것에도 적용할 수 있어 그 활용도가 높다고 할 수 있다. 향후, 본 연구에서는 제안 수법을 다양한 유체 시뮬레이션 가시화에 적용하여 그 타당성을 검증하고자 한다.