Recently, we have witnessed a growing interest in laser pointer interaction (LPI), which allows users to interact directly from a distance through a laser pointer. In laser pointer-based interaction systems, the captured laser spot is recognized and used for interactions by using various image processing techniques. The advantage of ensuring movement flexibility for users has led to the widespread use of this method for multimedia presentations [1-4], robot navigation [5-7], medical purposes [8], virtual reality systems [9,10], and smart houses [11].
Recently, Kim et al. [2] summarized three fundamental problems with LPI: laser spot detection, interaction function, and coordinate mapping. In [11-13], the researchers focused on the development of a laser spot detection algorithm that directly influences the performance of LPI systems. The most difficult challenges of laser spot detection are strong light environments, real-time implementation, and dynamic backgrounds. For example, the background information always changes when the speaker turns the slides in practical presentation cases.
To overcome the above mentioned problems, two types of algorithms, namely target search (TS) and background subtraction (BGS), have been developed to detect a laser spot. The TS method directly searches the laser spot without considering the background. Shin et al. [12] simply searches for pixels with maximum intensities to detect the location of the laser spot. Chávez et al. [11] used a combination of template matching and fuzzy rule-based systems to improve the success rate of laser spot detection. Geys and Van Gool [13] determined the laser spot by using clusters along with the fact that a group effect is caused on laser spots by hand jitters. However, the TS method fails because of the strong light environment and the appearance change of the moving laser spot. On the other hand, BGS covers a set of methods that aim to distinguish between the foreground and the background areas by utilizing a background model. The traditional models used to represent background include statistical models, neural networks, estimation models, and some recent models including fuzzy models, subspace models, transform domain models, and sparse models [14]. Among them, sparse models have been successfully applied in compressive sensing [15]. Cevher et al. [16] considered background subtraction as a sparse approximation problem and provided different solutions based on convex optimization. Hence, the background is learned and adapted in a low-dimensional compressed representation, which is sufficient to determine spatial innovations. Huang et al. [17] proposed a new learning algorithm called dynamic group sparsity (DGS). The idea is that the nonzero coefficients in the sparse data are often not random but tend to be a cluster such as those in the case of foreground detection. However, the dictionary of backgrounds is constructed simply by using video frames that make this model sensitive to noise and background changes. In order to solve the problem of background changes and outliers in training samples, Zhao et al. [18] formulated background modeling as a dictionary learning problem. However, the learning process is time consuming and needs all the background information, which makes it difficult to apply in practice. Therefore, to solve the problem discussed in [18], we propose a novel robust algorithm for the construction and update of a dictionary for laser spot detection. Subsequently, the proposed model can control the varying backgrounds and the real-time performance.
The remainder of this paper is organized as follows: Section II briefly explains the proposed method of background modeling and foreground detection. In Section III, we show the experimental results in comparison with those of the existing methods, and some conclusions of the proposed method are presented in Section IV.
Suppose that we have an image
where
Suppose that we have
where
Zhao et al. [18] summarized two assumptions for this sparse model:
On the basis of these two assumptions, the BGS problem can be interpreted as follows: given a frame
where ║
Since Eq. (3) is an NP-hard problem because of the non-convexity of
Considering the LPI application, the foreground (laser spot) generally occupies a far smaller spatial area than the background. Therefore, we can simply treat the foreground as noises and obtain a Lasso problem:
This problem can be easily and rapidly solved using least angle regression (LARS) [19], and then, we can obtain the foreground using
To make the sparse model robust against dynamic backgrounds, the dictionary must be able to represent all the backgrounds. Huang et al. [17] assumed that background subtraction has already been performed on the first
However, in LPI applications, we are unable to collect a sufficient number of training samples. For example, we are unable to capture a large number of backgrounds in a presentation application since we do not know the information of the next slide until the user gives the ‘PageDown’ or ‘PageUp’ command. Besides, solving this optimization problem is time consuming and the solution is difficult to implement in real-time.
Since the use of video sequences as a dictionary is sensitive to noise, we use information from multiple frames for ensuring robustness. Therefore, the strategy is to apply an exponentially decaying weight to run an online cumulative average on the backgrounds:
where
The dictionary needs to update quickly in order to handle the occurrence of a new background. Huang et al. [17] set a time window to update the dictionary. For frame
Zhao et al. [18] assumed that the atoms in
Considering that when a new background occurs, the foreground
Where
The proposed strategy is made sensitive to changing backgrounds by adding new background configurations, and robust against noise by using the online cumulative average of the backgrounds. The proposed dictionary construction and update algorithm is summarized in Table 1.
[Table 1.] Description of the proposed dictionary construction and update algorithm

Description of the proposed dictionary construction and update algorithm
To validate the ability of the proposed algorithm to handle the above mentioned high-frequency background changes and evaluate the algorithm’s real-time performance, in this section, we discuss two experiments of LPI. Through these experiments, we evaluated the performance of the proposed algorithm with the different parameters used in this algorithm, measured the detection error under dynamic backgrounds, and compared it with the running times of different algorithms as well.
>
A. Laser Pointer-Operated Windows
A typical example of LPI in practice is the interactive demonstration of software with a computer whose screen content is sent to a video beamer by using a common laser pointer tracked by a video camera as an input device. Algorithms use the behavior of the laser spot to realize the functions of Button Press, Button Release, and Mouse Move. When Button Press is recognized, the corresponding file or dialog may show up, which leads to a background change immediately. We record three videos of the size 160×120, 320×240, and 640×480, respectively, to simulate this process on such a system.
In LPI, the laser spot cannot be static because of the hand jitter, thus instead of measuring the detection error compared with the ground truth, we validate it using the possibility of false detected frames as follows:
The performance of the proposed algorithm is compared with that of two algorithms representing state-of-the-art sparse model approaches [17,18]. Notice that we use LARS [19] to solve Eq. (5) for all these methods in order to evaluate the dictionary construction and update approach. Fig. 1 illustrates some results of the abovementioned algorithms.
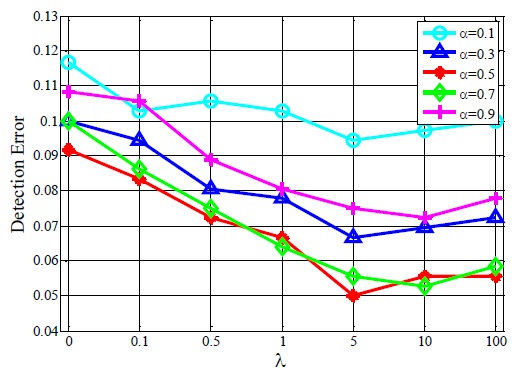
Image sequences having a size of 320×240 are used to test how the parameters
As can be observed in Fig. 2, a moderate
As the other parameter values used in these tests, we select
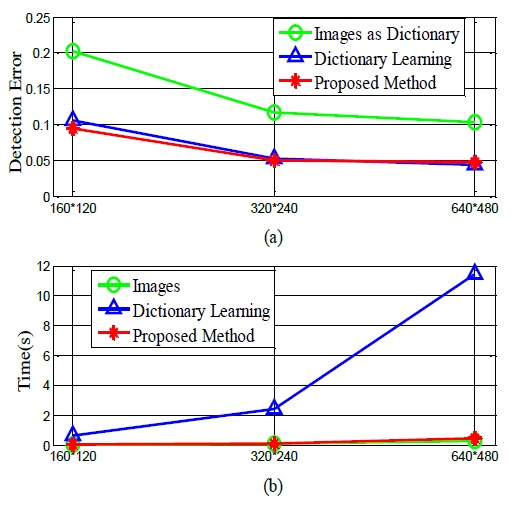
In a presentation application, we can use the laser pointer to change slides and draw lines. It should be noted that high-frequency changes are caused when the user changes the slides. Further, each slide may be totally different from the others. For this application, we manually change the slides to obtain dynamic backgrounds and use the above mentioned algorithms for the detection of the laser spot. The final results are shown in Figs. 4 and 5.
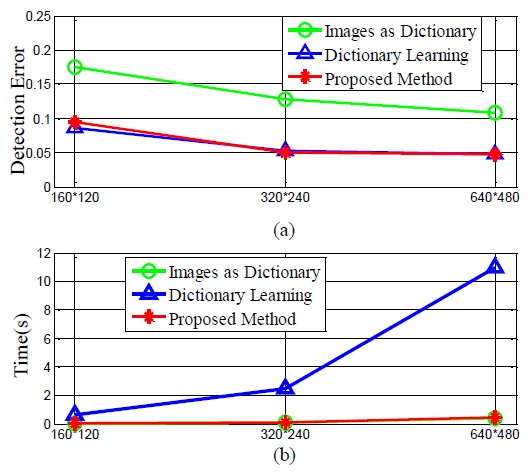
From Figs. 4 and 5, we can see that the proposed algorithm can achieve a lower detection error with a low time cost, which is similar to the results of the laser pointer-operated windows method. Thus, the proposed algorithm is robust against different scenarios with dynamic backgrounds. From Table 2, we can see that the detection error when the image resolution 160×120 is the highest, while similarly low detection errors are obtained when the resolutions of 320×240 and 640×480 are used. However, the time cost of using the resolution of 640×480 is considerably higher than that of using the resolution of 320×240. Thus, we recommend the use of the 320×240 resolution in practice.
[Table 2.] Performance comparison of different image resolutions

Performance comparison of different image resolutions
In this paper, we focus on the laser spot detection algorithm and model it as a background subtraction problem. Further, we propose a robust dictionary construction and update algorithm based on the sparse model for laser spot detection. To test the performance of the proposed method, a large number of experiments are conducted from the perspectives of detection error and real-time performance. The experimental results confirm that the proposed method outperforms the existing methods with a lower detection error and better real-time performance when the background exhibits a high frequency of changes.
Finally, the proposed robust algorithm can also be applied to solve other practical problems, such as traffic monitoring [18] where the background switches among several configurations controlled by the status of traffic lights.


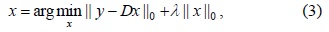
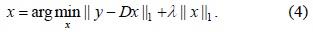
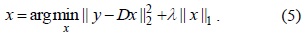

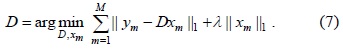
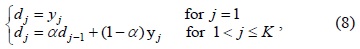
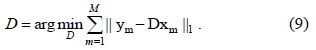
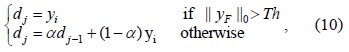

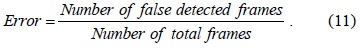
![Results on laser pointer-operated Windows. (a) Original image (size: 320×240). (b) Using video images as dictionary [17]. (c) Dictionary learning method [8]. (d) Proposed method.](http://oak.go.kr/repository/journal/17267/E1ICAW_2015_v13n1_42_f001.jpg)
![Results of multimedia presentation. (a) Original image (size: 320×240). (b) Using video images as dictionary [17]. (c) Dictionary learning method [18]. (d) Proposed method.](http://oak.go.kr/repository/journal/17267/E1ICAW_2015_v13n1_42_f004.jpg)