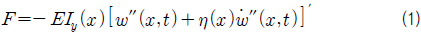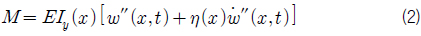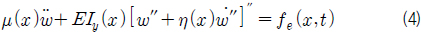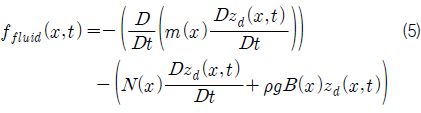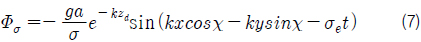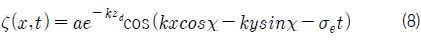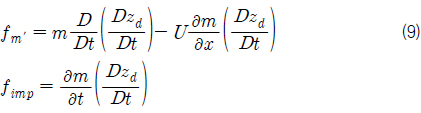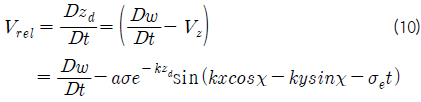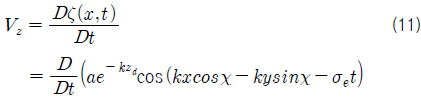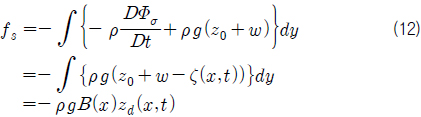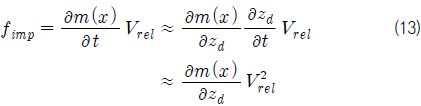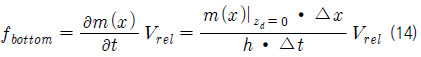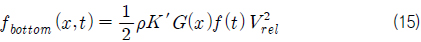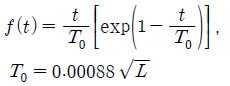This paper describes the time-domain numerical method for prediction of slamming loads on a ship in waves using the strip theory. The slamming loads was calculated considering the relative vertical velocity between the instantaneous ship motion and wave elevation. For applying the slamming force on a ship section, the momentum slamming theory and the empirical formula-based bottom slamming force were used corresponding to the vertical location of wetted body surface. Using the developed method, the vertical bending moments, relative vertical velocities, and impact forces of S175 containership were compared in the time series for various section locations and wave conditions.
슬래밍(slamming)은 파랑 중 항해하는 선박의 운동과 입사파와의 운동 변위차이로 인해 발생하는 충격 현상으로, 선체의 일시적인 진동현상인 휘핑(whipping)을 야기 시키는 주요 요인이다. 따라서, 슬래밍은 선체의 국부적인 손상뿐만 아니라 종강도 및 피로강도에 크게 영향을 미치게 된다. 특히 최근 건조 되고 있는 대형 컨테이너 선박은 기존 선박의 선형과 상이하여, 항해 조건이나 해상 상황에 따라 매우 심각한 슬래밍 현상이 발생할 수 있다. 따라서 초기 설계 단계에서 선형에 따른 슬래밍 현상의 발생과 선체 구조 강도에 미치는 영향을 정확히 예측하여 건조 선박의 안정성과 내항성을 확보 하는 것이 필요하다.
슬래밍은 크게 2가지로 구분할 수 있는데, 선체가 수면 밖으로 노출되었다가 재 입수시에 발생하는 선저 충격 슬래밍(bottom impact slamming)과 항해하는 선박의 선수부에서 입사파에 의한 선수 플레어 슬래밍(bow flare slamming)이 있다.
슬래밍에 대한 초기연구로서 Ochi and Motter (1973)는 슬래밍 현상을 선박의 초기 설계 단계에서 고려할 수 있도록 그 특성을 세분하여 선체 충격하중에 대한 통계적인 예측방법을 제시하였다. 최근에 슬래밍 충격하중에 대한 관심이 증가함에 따라 여러 실험적인 연구들이 진행되었다 (Nahm, et al., 2007; Park, et al., 2009; Kwon, et al., 2013). 또한, Lee, et al. (2007)은 선체에 발생하는 슬래밍 현상을 실질적이고 정도 높은 예측을 위해 북태평양과 유럽 항로상을 항해하는 대형 컨테이너선에 압력계를 설치하고 선수 플레어 슬래밍의 충격압력을 실제로 계측하여 슬래밍 특성을 연구하였다. 또한, Shin, et al. (2010)은 경사각을 갖고 자유 낙하하는 쐐기형태의 모델 실험을 통해, 선체에 가해지는 슬래밍 충격 하중의 정확한 물리적 현상과 특성을 파악하고자 최대 충격 압력, 최대압력부의 지속시간 및 압력 이동속도 등을 계측하였다.
수치해석을 통한 슬래밍 하중 추정에 대한 초기연구로서 Yamamoto, et al. (1979)은 탄성체로 가정한 선체에 대해 모멘텀 슬래밍 이론을 적용하여 파랑하중을 추정하였다. 최근에 Hwang, et al. (2012)도 선체를 길이 방향으로 불균일한 단면을 가지는 Bernouli-Euler 보로 간주하고 모멘텀 슬래밍 이론을 이용하여 파랑하중을 산정하고 시간영역에서 선체 진동 방정식을 계산하였다. 또한, Modal 해석을 통해 선체에 작용하는 고차진동을 계산하였으며, Lewis form method를 사용하여 매 시간 스텝마다 변화된 선체 침수 단면에 대한 동유체력 계수를 계산하였다.
본 논문에서는 기존에 개발된 수치 해석 방법인 Hwang, et al. (2012)의 연구를 발전시켜, 매순간 변화하는 선체와 수면간의 상대 수직 속도를 고려하여 선체 위치에 따라 모멘텀 슬래밍과 충격 슬래밍을 각각 적용하여 슬래밍에 의한 파랑 하중 산정의 타당성과 정확성을 높여, 보다 정밀한 충격하중 예측과 선체조건 (강체 및 탄성체 조건)에 따른 선체 운동을 계산하고 이를 비교 분석하였다. 슬래밍 현상에 의한 파랑하중 추정은 아직까지 복잡한 유체력 산정의 난해함으로 이론적 추정이 어렵다. 특히 선저 충격 슬래밍은 선저구배를 고려하고 공기완충 효과 등이 포함되는 복잡한 현상이기 때문에 이론적 방법 보다는 실험에 의한 경험식이 많이 사용된다. 이러한 이유로 본 연구에서는 Ochi and Motter (1973)의 제안에 따라 선저부터 1/10 흘수까지는 경험식에 근거한 충격 슬래밍(impact slamming) 이론을 사용하여 선저 충격하중을 산정하였고, 그 이상의 흘수에서 발생하는 선수 플레어 슬래밍은 모멘텀 슬래밍을 이론을 사용하여 슬래밍에 의한 선체 외력을 계산하였다.
2.1 지배방정식(Governing equation of vibration)
슬래밍에 의한 파랑하중 산정과 이에 따른 선체의 운동 응답을 계산하기 위해 스트립 이론을 바탕으로 선체를 불균일한 단면을 가지는 Bernouli-Euler 보로 간주하여 선체의 운동 방정식을 구하였다. 이같은 가정은 Bernouli-Euler 보 이론이 하중에 의한 보의 변위 특성을 파악하는데 유리하며, 상대적으로 작은 변위에 대해 간편하게 계산할 수 있기 때문이다. 선체를 길이방향으로 미소 길이
여기서 ,
이들을 대입하여 정리하면 다음과 같은 진동방정식(식 (4))을 얻을 수 있다. 여기서
선체 양끝 단(
선체에 작용하는 외력
여기서
본 연구에서는 계산 영역 내의 유체를 이상유체로 가정하였고, 심해 조건에서 선박 속도와 입사파 간의 조우주파수 (
여기서
선체에 작용하는 유체 관성력 (
슬래밍에 의한 유체충격력 계산에서 중요한 변수인 상대 수직 속도
여기서
유체 정력학적 힘과 Froude-Krylov 힘의 합인
여기서
슬래밍에 의한 선체 충격 하중
모멘텀 슬래밍 이론에 의한 플레어 슬래밍 충격력은 선체 운동에 의한 부가질량
하지만 모멘텀 슬래밍 이론을 이용하여, 선체가 수면에 재 입수하는 순간 선저부에서 발생하는 선저 충격 하중
따라서, Hwang, et al. (2012)은 모멘텀 슬래밍 이론을 이용하여 선저 충격 하중
하지만, 서론에서 언급한 바와 같이 선저 충격하중의 예측은 계산 조건의 단순화를 통한 수학식으로 표현하기에는 아직까지 그 정확성에 한계가 있다. 따라서, 본 연구에서는 선저 충격하중의 보다 정확한 계산을 위해, 경험식에 근거한 선저 충격 하중식 (15)를 도입하여 선저부터 1/10흘수까지 선저 충격 외력을 계산하고 (Choi, et al., 2012), 그 이상의 흘수에서는 모멘텀 슬래밍 이론에 의한 충격 하중
여기서,
본 연구에서는 슬래밍에 의한 파랑하중을 정확히 산정하기 위해 모멘텀 슬래밍 이론과 선저 충격 슬래밍 이론을 선체의 흘수 위치에 따라 각각 적용하였으며, 선체와 파면의 상대수직속도를 고려하여 계산하였다. 고파고 등의 조건에서 스트립 이론을 이용하여 선형에 따른 선체 각 단면의 정확한 계산을 위해 21개의 단면을 101개로 세부 분할하였으며, 선저 충격 하중은 실험에 근거한 경험식을 사용하여 전체 파랑하중에 미치는 영향을 분석하였다. 101개 세부 분할 단면의 계산 결과는 이해의 편의성을 위해 기존의 21개 단면에 대한 비율로 나타내었다 (예, 97~101번 세부 분할 단면은 21번 단면임).
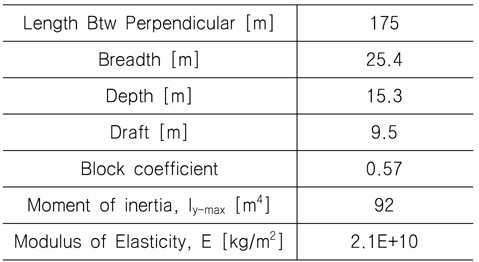
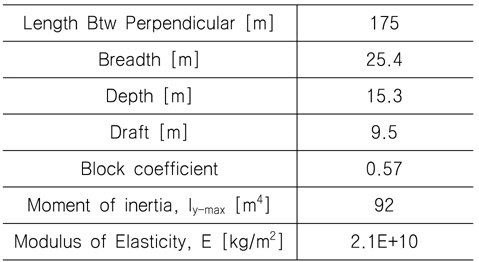
본 계산에 사용한 선박은 잘 알려진 S175 형이며 Table 1에 선체의 주요제원을 표시하였다. 선형에 대한 일반적인 계산 조건은 앞선 연구 (Hwang, et al., 2012) 에서 적용한 조건과 동일한다. 이를 간략하게 언급하면, 선체 길이 방향의 중량 분포는 각 단면의 무게분포와 부력분포가 같다고 가정하였고, 단면의 2차 모멘트에 대한 선체 길이방향의 분포는 사다리꼴 형상으로 가정하여 5번째 단면에서 13번째 단면 (21~66 세부 분할 단면)까지는 최대값으로 일정하고 선수와 선미 방향으로 선형적으로 감소하여 선수와 선미에서 0으로 가정하였다. 또한, 선체는 강철로 구성되어 있다고 간주하여, 탄성계수(E)는 2.1x1010을 사용하였고, 구조감쇠계수 계산을 위한 대수감소율(δ)는 일반적으로 알려진 값인 0.056를 사용하였다.
[Table 1] Principal dimensions of S175 container ship
Principal dimensions of S175 container ship
계산 조건은 입사파장과 선체길이의 비(λ/L)를 1.2, 선속은 Froude number (Fn)를 0.275로 가정하였으며, 파경사 ka는 0.01, 0.08, 0.12, 0.18로 파고를 순차적으로 증가시켜 대입함으로써 파고 증가에 따른 슬래밍 파랑하중의 변화를 비교하였다.
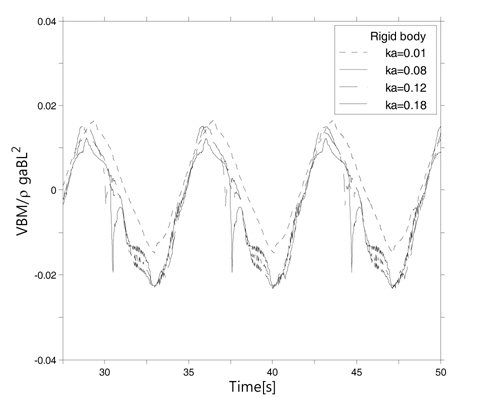
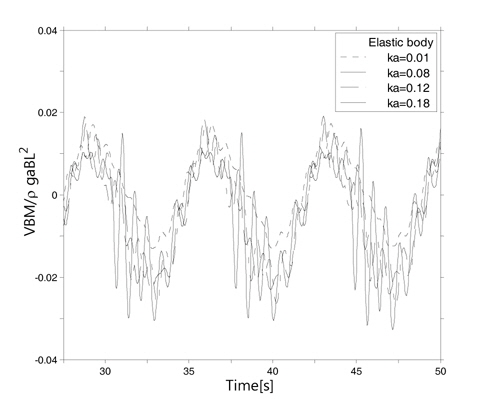
슬래밍에 의한 파랑하중 계산을 위해 모멘텀 슬래밍 이론의 충격 하중 식과 경험식에 기반한 선저 충격 하중식을 매 순간 선체 각 단면의 흘수 위치에 따라 각각 적용하여 유체력을 계산하고 이에 따른 선체의 수직 굽힘 모멘트를 파고의 변화에 따라 시간 영역에서 비교 하였다. Fig. 1는 선체가 강체라는 가정하에 파고의 증가에 따른 수직 굽힘 모멘트의 변화를 비교한 결과이다. 파고가 작은 경우 (ka=0.01), 시간에 따른 수직 굽힘 모멘트의 변화는 최대값과 최소값의 평균 합이 0 에 근접하는 선형 계산 결과에 가까워짐을 확인할 수 있지만, 파고가 증가할수록, 즉파 기울기가 커질수록 수직 굽힘 모멘트의 평균 값이 0에서 멀어지며 불규칙 성분이 커지는 것을 알 수 있다.
특히 본 계산의 최대 파고 (ka=0.18)에서 불규칙 성분이 급격하게 증가하는 것을 확인할 수 있다. 선체를 탄성체로 가정하여 수직 굽힘 모멘트의 시간 변화를 비교한 Fig. 2에서는 파고가 증가할수록 선체의 진동 성분이 점차적으로 증가함을 확인할 수 있다. 특히 최대 파고에서 선체 진동으로 인한 수직 굽힘 모멘트의 급격한 변화를 확인할 수 있으며, 증감폭이 전체 굽힘 모멘트의 진폭과 거의 같은 크기로 진동함을 알 수 있다. 이는 선체가 탄성체일 때 파고 증가에 따른 굽힘 모멘트의 급격한 변동을 예상할 수 있는 것으로서, 이에 따른 선체의 국부 하중 증가와 피로 현상의 증가를 예측할 수 있다.
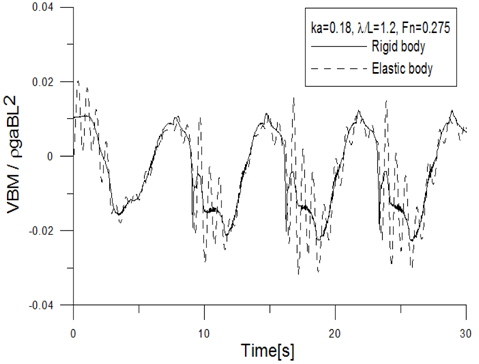
최대 파고 적용시, 선체의 진동 조건 (강체와 탄성체 조건)에 따른 선체 중앙부에 작용하는 수직 굽힘 모멘트를 Fig. 3에서 비교하였다. 선체의 진동 조건에 관계없이 두 조건 모두에서 불규칙 성분이 명확하게 나타나는 것을 확인할 수 있다. 하지만, 선체를 탄성체로 가정한 경우, 입사파 주기에 비해 빠르게 진동하는 고차항의 진폭이 파 주기에 따른 모멘트의 변동폭과 유사하거나 오히려 더 크게 나타남을 알 수 있다.
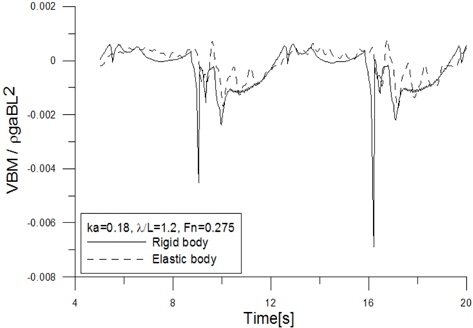
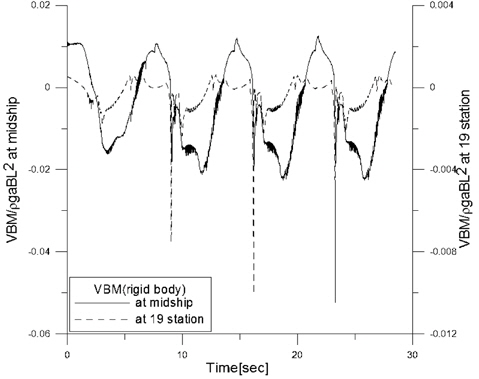
Fig. 3와 같은 조건에서, 선수부인 19번째 단면 (87~91번 세부 분할 단면)에서 최대 파고시 수직 굽힘 모멘트를 Fig. 4 에서 비교 하였다. 선체 중앙부에서의 변동 패턴과 유사하게 불규칙 성분이 뚜렷하게 증가한 것을 알 수 있다. 선체가 탄성체인 경우와 달리, 선체를 강체로 간주하여 계산한 경우 파 주기에 상응하는 매우 급격한 진동 성분이 관찰되는데 이는 선저 충격 하중이 선수부의 수직 굽힘 모멘트 증가에 직접적인 영향을 줌을 의미한다. 좀 더 자세히 분석을 위해, 강체 조건에서 선체 중앙부와 선수부에 대한 수직 굽힘 모멘트의 변동을 각각의 수직축을 대상으로 Fig. 5에서 비교 하였다. 선저 충격하중에 의해 선체 중앙부의 수직 굽힘 모멘트의 증가와 선수부의 급격한 수직 굽힘 모멘트의 증가가 동 시간에 발생하는 것을 확인할 수 있었는데, 이는 선수부의 수직 굽힘 모멘트와 선체 중앙부의 수직 굽힘 모멘트간에 밀접한 연관성이 있음을 예상할 수 있다.
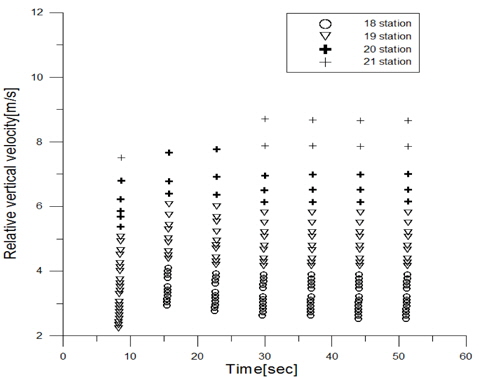
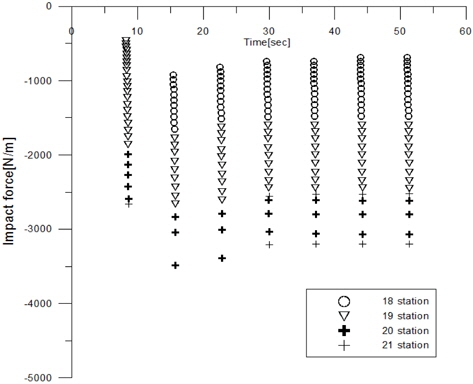
선수부에 작용하는 선저 충격 하중의 영향에 대한 분석을 위해 선수부 단면에서 슬래밍으로 인해 충격하중이 발생하는 순간의 상대 수직 속도(Fig. 6)와 이 때의 충격력(Fig. 7 and Fig. 8)을 시간영역에서 비교하였다. 선저 충격 슬래밍이 발생하는 조건인 Fn=0.275, 파장 대 선체 길이의 비 1.2, 그리고 파기울기(ka)는 0.12인 경우를 산정하였다.
선저 충격 슬래밍은 선박이 아랫방향 (양의 방향) 이고 수면이 윗방향 (음의 방향)으로 움직일 때 발생하기 때문에, 선저 슬래밍 발생시 상대 수직 속도는 양의 값을 가진다. Fig. 6에서 선저 충격 슬래밍이 발생 할 때 각 단면에서의 상대 수직 속도는 선수 가장 앞부분인 21번째 (97~101번 세부 분할 단면) 단면에서 약 9m/s로 상대 수직 속도가 가장 빠른 것을 알 수 있다.
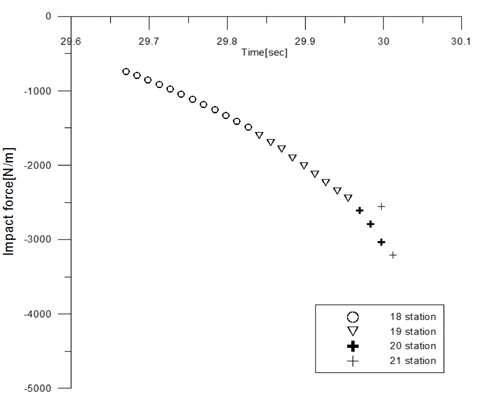
Fig. 7은 상대 수직 속도의 제곱에 비례하는 선저 충격 하중을 각 단면에 따라 시간 영역에서 비교하였다. 또한, Fig. 8에서는 선저 충격 하중을 보다 자세히 관측하기 위해 슬래밍 발생 순간 (29.6~30.1sec)의 충격 하중의 변화를 확대 비교하였다. 이를 통해 순간 충격력은 선체가 재입수하는 시간 동안 (18번 단면에서 21번 단면으로 선체 입수면 이동)에 따라 2차항 곡선 형태로 점점 그 크기가 급격히 증가하는 것을 알 수 있고, 상대 수직 속도가 가장 큰 선수부 끝단면 (21번째 단면)에서 가장 큰 값을 가짐을 확인할 수 있다.
이상의 계산 결과를 통해, 본 연구에서 개발된 슬래밍에 의한 선체의 충격 운동 응답 계산 기법은 매우 짧은 시간에 선체에 발생하는 충격 하중과 이에 따른 선체 응답을 시간영역에서 정밀하게 분석할 수 있음을 보여주고 있다. 본 기법을 활용하면, 파랑 중 선체에 작용하는 슬래밍 현상과 충격하중 산정, 이에 따른 선체의 운동 특성을 보다 정밀하게 분석할 수 있을 것이다.
파랑 중 선체에 작용하는 슬래밍 하중을 선체운동과 입사파 수면의 상대속도를 고려하여 계산하고 이에 따른 선박의 충격 운동 응답 해석을 수행하였다. 스트립 이론을 사용하여 선체를 101개 단면으로 분할하여 계산하였으며, 슬래밍에 의한 충격 하중을 보다 정밀하게 산정하기 위해 매 순간 선체 단면의 상대 수직 변위 위치에 따라 모멘텀 슬래밍 이론과 경험식에 기반한 선저 충격 슬래밍 계산법을 적용하는 수치 해석 기법을 개발하였다.
본 연구에서 개발된 계산 기법을 이용하여, S175형 선박의 중앙 단면과 선수부의 각 입사파 조건에 따른 수직 굽힘 모멘트의 변화를 비교하였다. 또한, 선체의 진동 조건 (강체 및 탄성체 조건)에 따른 수직 굽힘 모멘트의 변화를 비교 하였다. 파고가 증가할수록 선체 진동 조건에 관계없이 수직 굽힘 모멘트의 불규칙 성분이 증가하였고, 특히 탄성체로 간주한 선체 조건에서는 입사파 주기에 비해 빠르게 진동하는 고차항의 진폭이 파 주기에 따른 모멘트 변동폭과 유사하거나 오히려 더 큰 것을 확인 하였다.
강체 조건의 계산에서, 선저 충격 하중이 선수부의 급격한 수직 굽힘 모멘트의 증가에 직접적인 영향을 줌을 확인하였고, 선수부와 중앙 단면의 수직 굽힘 모멘트의 증가는 서로 밀접한 연관성이 있음을 확인 하였다.
선저 충격 슬래밍이 발생 할 때 선수부 앞쪽 단면일수록 상대 수직 속도가 빨라지고, 이에 따른 충격력은 2차항 곡선 형태로 급격히 증가함을 확인하였다.
이상의 연구 결과를 통해, 본 연구에서 개발된 슬래밍 하중에 의한 선체의 충격 운동 응답 기법을 활용하면, 매우 짧은 시간에 선체에 작용하는 충격 하중과 운동 특성을 시간영역에서 분석할 수 있으며, 선체 단면 위치에 따른 슬래밍 하중과 특성을 보다 구체적으로 파악할 수 있을 것이다.