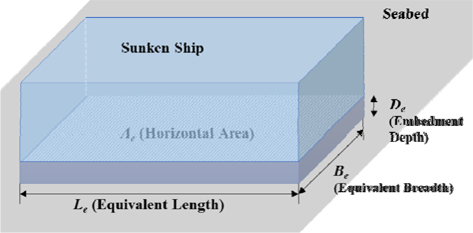
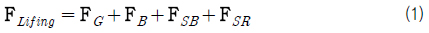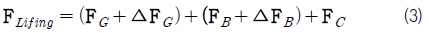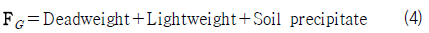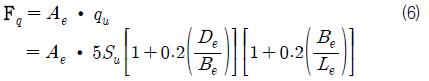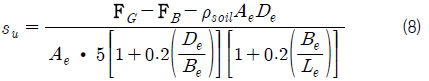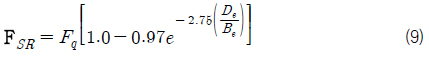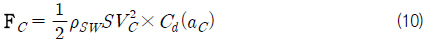선박이 침몰한 이후 선 내 남아있는 원유에 의한 오염을 방지하여 환경적인 피해를 막고, 사고의 원인을 파악하여 추가적인 사고를 예방하기 위해 침몰 선박의 인양이 필요하다. 선박의 인양을 위해서는 여러 가지 사항이 고려되어야 한다. 우선 선박 내부로 해수가 유입되기 때문에 부력이 거의 상실된 상태에서 침몰 선박의 중량과 내부에 있던 화물의 이동에 따른 무게 중심의 위치를 파악해야 한다. 그리고 안전을 고려한 다양한 인양 방법이 검토되어야 한다. 인양 방법이라 함은 인양을 위해 이용할 해상 크레인과 같은 장비를 선정하고, 인양 시 침몰 선박과 장비의 연결 방법을 선택하는 것이다. 장비 연결 시 대부분 체인 또는 와이어 로프가 사용되며, 이때 작용하는 하중을 정확히 계산할 필요가 있다. 그렇지 않을 경우 인양 중 체인 또는 와이어 로프가 끊어진 사고가 발생할 수 있다.
인양 방법에 대한 여러 가지 대안이 선정되면 각 대안이 실제로 적용 가능한지에 대한 인양 시뮬레이션이 필요하다. 인양 시뮬레이션의 범위는 해저면에서부터 침몰 선박을 이탈시킨 뒤 해수면까지 들어올리는 전체 과정을 의미한다. 예를 들어 해상 크레인을 이용하여 인양을 한다고 가정하였을 때, 해상 크레인의 각 와이어 로프에 작용하는 하중에 따라 인양 가능 여부의 판단 및 안전 계수 등의 계산을 시뮬레이션을 통해 수행할 수 있다.
인양 시뮬레이션에서 가장 중요한 것은 바로 인양력(lifting force)의 추정이다. 인양력을 계산할 때 침몰 선박이 들어 올려지는 과정에 따라 고려되어야 할 환경적 요소, 즉 환경 하중은 크게 세 가지로 나눌 수 있다. 첫 번째는 침몰 선박이 놓여져 있는 지역의 해저 저질(seabed sediment)이다. 침몰 선박의 일부가 해저에 묻혀있는 경우에는 선박과 화물에 의한 하중 외에도 해저면으로부터 침몰 선박을 이탈(breakout)시키는 데 상당한 힘이 필요하다. 두 번째는 해당 지역의 조류(current)이다. 침몰 선박을 들어 올리는 동안 조류에 의한 힘이 선박에 작용하게 된다. 마지막으로 세 번째는 침몰 선박이 해수면 밖으로 나오면서 공기와 만나는 시점에 변화하는 부력이다. 해수면으로부터 선박이 나오게 하면 공기와 물의 밀도 차이 때문에 선박의 부력 변화가 발생하며 이는 인양력에 영향을 미치게 된다.
본 연구에서는 인양 과정 중 작용하는 다양한 환경 하중을 고려하여 침몰 선박의 물리 기반 시뮬레이션을 수행함으로써 인양 과정 중 발생할 수 있는 문제점을 사전에 파악해 보고자 하였다.
본 논문은 다음과 같이 구성되어 있다. 2장에서는 인양력 및 인양 시뮬레이션과 관련된 연구 현황에 대해 살펴본다. 3장에서는 인양 방법을 검토하기 위한 일반적인 과정에 인양 시뮬레이션의 활용할 수 있는 방안을 설명하고, 4장에서는 인양력을 계산하는 방법을 기술한다. 5장에서는 인양력을 포함한 인양 시뮬레이션 프로그램에 대해서 설명하고, 이를 예제에 적용한다. 마지막으로 6장에서는 결론 및 향후 연구 계획에 대해서 설명한다.
Lee (2014)는 침몰 선박의 인양 하중 추정 시 다양한 환경 하중을 고려하였고, 이를 실험을 통해 검증하였다. 하지만, 실제 인양 전 과정에 대한 시뮬레이션은 고려하지 않았다.
Byun, et al. (2001)은 해저 바닥에 놓인 침몰 선박에 대해 이를 해저 저질로부터 이탈시키기 위한 이탈력을 Terzaghi-Meyerfhof식을 이용하여 계산하였고 이를 위한 프로그램을 개발하였다. 개발된 프로그램은 단순히 초기 이탈력만을 계산하기 때문에 인양 시뮬레이션에는 적합하지 않다는 한계가 있다.
Bartholomew (1992)는 인양에 영향을 미치는 여러 가지 요소 중 환경적 요소에 대해 이론적으로 정리하였다. 하지만 외력의 계산 결과만 있을 뿐 인양 중 동적 거동에 대한 고려는 하지 않았다.
Choi, et al. (2000)은 선박을 인양할 때 와이어 로프의 위치, 선박의 기울기, 무게 중심을 고려한 운동 방정식을 풀어, 인양 시 각각의 와이어 로프에 걸리는 장력을 계산하는 방법을 제시하였다. 하지만, 해저 저질을 고려한 초기 인양력이나 조류와 같은 환경 하중은 고려하지 않았다.
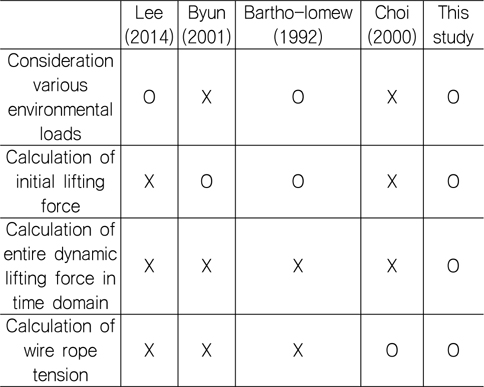
본 논문에서는 해저 저질을 포함한 환경 하중을 고려하여 인양 전 과정에 대한 물리 기반 시뮬레이션을 수행하였고, 이를 위한 프로그램을 개발하였다. 선행 연구와 비교를 아래 Table 1에 정리하였다.
[Table 1] Comparison of this study with related works
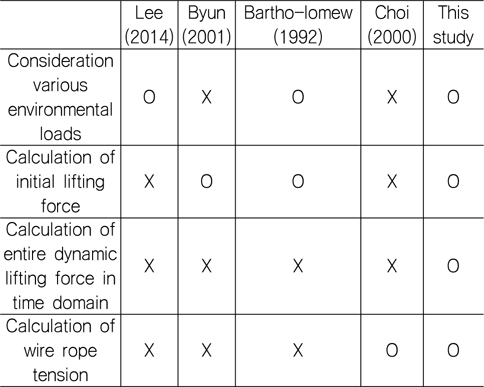
Comparison of this study with related works
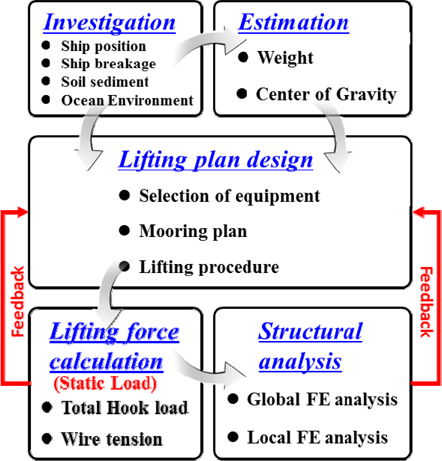
침몰 선박의 효과적인 인양 방법을 결정하기 위해서는 일반적으로 Fig. 1의 과정을 반복하게 된다. 우선 탐사(investigation)를 통해 침몰 선박이 해저면에 놓여 있는 위치, 자세, 파손 여부 및 해저 저질의 종류, 날씨 등 해역에 대한 조사를 수행한다. 다음으로 침몰 선박의 초기 출항 상태 시 화물 적재량과 침몰 시 자세 파악을 통해 중량(배수량)과 무게 중심을 예측(estimation)한다. 탐사 및 예측 정보를 바탕으로 인양 계획(lifting plan)을 수립하게 된다. 방안이 선택되면, 인양 시 장비에 작용하는 하중과 침몰 선박의 선체와 연결된 와이어 로프에 작용하는 장력 등이 계산(lifting force calculation)된다. 이를 바탕으로 구조적으로 안전한지 여부를 확인(structural analysis)하여, 그 결과를 다시 인양 계획에 반영한다.
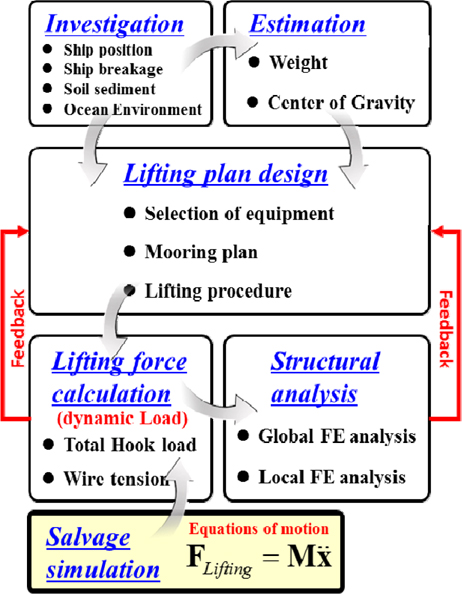
위 과정 중 인양력 계산은 지금까지 정적 하중 분석 방법(static load analysis)에 의존해 왔다. 따라서 실제 작업 중에 발생하는 동적 하중(dynamic load)을 예측하는 데에는 한계가 존재하였다. 만약 시뮬레이션을 통해 동적 하중을 예측할 수 있다면 Fig. 2와 같이 이를 포함한 개선된 인양 절차를 고려할 수 있다. 즉, 인양 시뮬레이션(salvage simulation)의 계산 결과를 활용하여 인양 하중을 계산함으로써 동적 하중을 인양 계획 수립 시 반영할 수 있으며, 이를 통해 보다 안전한 인양 계획의 수립이 가능하리라 생각된다.
4장에서는 침몰 선박의 인양 시 필요한 인양력의 구성과 인양력의 각 성분을 계산하는 방법을 설명한다.
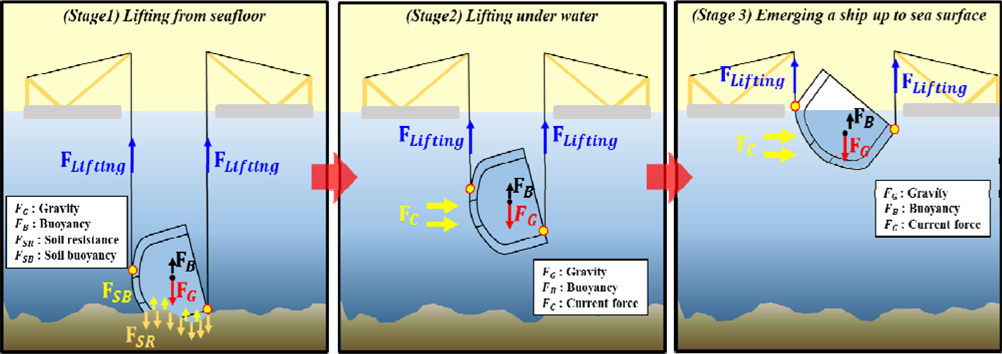
1장에서 언급한 것과 같이 인양력은 고려해야 할 환경적 요소 및 침몰 선박의 위치에 따라 크게 3단계로 나눌 수 있다.
Stage 1: Lifting from seabed
해저 저질의 종류에 따라 차이를 보이지만, 일반적으로 침몰 선박의 경우 해저 저질에 박혀있게 된다. 박혀 있는 물체를 뽑기 위해서는 자중 이외에도 추가적인 힘이 작용하는데, 이를 이탈력(breakout force) 또는 해저 저질에 의한 저항력(soil resistance)이라고 한다. 또한 해저 저질 내에 박혀 있는 부분에는 해저 저질에 의한 부력이 작용한다. 따라서 1단계의 인양력은 식 (1)과 같이 계산될 수 있다.
위 식에서 FG는 중력, FB는 부력, FSB는 해저 저질에 의한 부력, FSR은 해저 저질에 의한 저항력이다.
(2) Stage 2: Lifting under water
해저 저질에서 이탈 후 수면까지 이동하는 중에는 조류력이 작용하게 된다. 따라서 2단계의 인양력은 식 (2)와 같이 계산될 수 있다. 여기서 FC는 조류력을 의미한다.
(3) Stage 3: Emerging the wreck up to sea surface
선체가 수면 밖으로 나오게 되면 내부에 머금고 있던 해수가 위로 올라오면서 일시적으로 중량이 늘어난 것과 같은 작용을 하게 된다. 이후 해수가 배출되면서 본래의 중량으로 돌아가게 된다. 즉, 이 과정에서 선체의 중량 변화가 발생한다. 또한 선체의 부력도 변화하는데, 물 밖으로 나온 부분에 의해 부력이 감소하게 된다. 이를 식으로 나타내면 식 (3)과 같다.
위에서 설명한 인양력의 각 성분을 그림으로 나타내면 Fig. 3과 같다.
침몰 선박의 중량은 선체와 의장의 무게에 해당하는 경하 중량(lightweight)과 적재된 화물 및 연료, 발라스트 수 등의 중량(deadweight)의 합과 같다. 한편, 침몰 선박 내에 유입된 해저 저질의 침전물(soil precipitate)도 선박의 중량에 포함된다. 따라서 침몰 선박의 중량은 다음과 식 (4)와 같이 구성된다.
선박이 침몰하기 전에는 아르키메데스의 원리에 의해 선박이 배제한 물의 무게에 해당하는 힘이 부력으로 작용한다. 하지만 선박이 침몰하게 되면 선박 내부에 물이 차면서 부력을 상실하게 된다. 선박이 침몰하여도 전체 부력이 상실되는 것은 아니다. 기본적으로 강판의 두께에 해당하는 부피만큼의 부력은 작용하게 된다. 물론 선박 내 적재된 화물, 밀폐된 탱크 등에 의해 추가 부력이 존재할 수 있으나 본 연구에서는 이를 무시하였다. 따라서 선박에 작용하는 부력은 다음 식 (5)와 같다.
여기서
해저 저질에 의한 저항력(F
여기서, F
식 (6)에서 지지력은 박힌 깊이에 따라 증가하게 된다. 따라서 처음 해저 바닥에 침몰 선박의 바닥이 닿게 되면 해저 저질에 의한 지지력이 선박에 작용하는 중력과 부력의 합보다 작기 때문에 점점 땅에 박히게 된다. 그러던 중 지지력과 선박에 작용하는 중력과 부력의 합과 같아지는 평형 상태에 도달하면 더 이상 박히지 않고 멈추게 된다(Fig. 4 참조). 따라서 이 경우, 해저 저질에 의한 부력(F
해저 저질에 박혀 있는 침몰 선박이 평형 상태에 있을 때의 지지력은 식 (7)과 같이 표현할 수 있다. 여기서 해저 저질에 의한 부력은 해저 저질의 밀도와 접촉 면적(
식 (6)과 식 (7)을 등식으로 놓고, 해저 저질의 전단 응력(
식 (8)에서
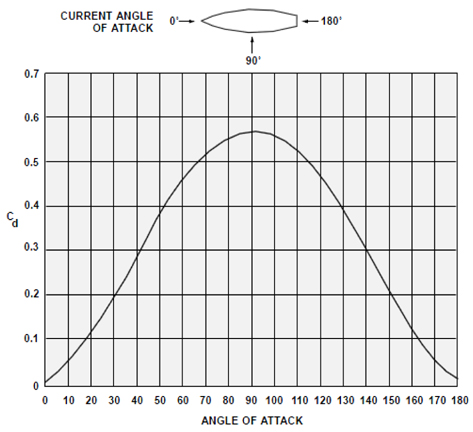
조류력은 일반적으로 다음과 같은 식 (10)과 같은 경험식으로 계산할 수 있다 (Bartholomew, 1992).
여기서,
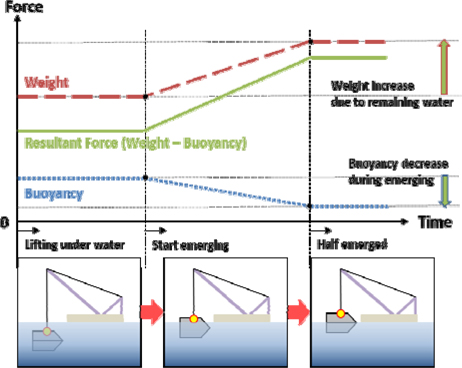
수면 밖으로 침몰 선박이 나올 경우 중량 및 부력의 변화를 고려해야 한다. 수면 바깥으로 들어 올려진 초기에는 선박 내부에 포함된 해수가 모두 추가적인 중량으로 작용한다. 이후 일정하게 해수가 배수되면서 선박의 중량은 감소하게 된다. 이때, 모든 해수가 배출되는 것은 아니고, 일부 해수는 닫힌 공간 내부에 머물게 되므로, 결국 중량은 일정하게 된다. 본 연구에서 해수의 배출량은 시간에 비례하여 일정하게 감소한다고 가정하였고, 그 중 일정 비율이 선박 내부에 남아있다고 가정하였다. 따라서 수면 밖으로 올라오는 중 침몰 선박의 중량은 시간에 따라 일정하게 증가한다. 한편, 부력 변화의 경우 수면 바깥으로 나온 선체의 비율을 고려하여 선박 강판 두께에 의한 부력이 감소한다고 가정할 수 있다. 이와 같은 개념을 그래프로 나타내면 Fig. 6과 같다. 즉, 중량은 선체 내부에 남아있는 해수의 영향으로 일정하게 증가하게 되고, 부력은 반대로 일정하게 감소하게 된다. 이에 따른 합력은 중량과 부력의 차이로 나타낼 수 있다.
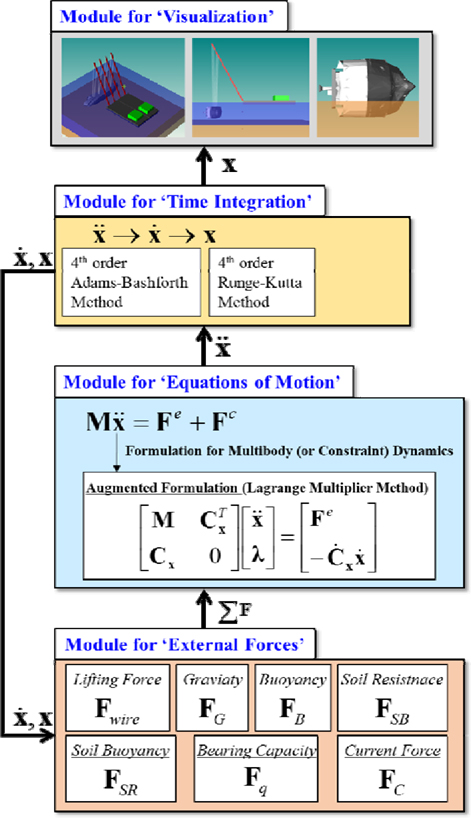
본 연구에서는 물리 기반 인양 시뮬레이션을 수행하기 위해 다음 4개의 모듈로 구성된 시뮬레이션 프로그램을 자체적으로 개발하였다.
- Module for ‘External Forces’: 4장에서 설명한 인양력을 계산하는 모듈 - Module for ‘Equations of Motion’: 계산된 인양력을 기반으로 장비와 침몰 선박의 가속도를 계산하는 모듈 - Module for ‘Time Integration’: 가속도를 수치적으로 적분하여 속도와 위치를 계산하는 모듈 - Module for ‘Visualization’: 매 시간마다 계산된 결과를 화면상에 가시화하는 모듈
각 모듈간의 관계와 자세한 구성도는 Fig. 7과 같다. 우선 각각의 인양력 성분을 계산하기 위해서는 'Time Integration'모듈에서 계산된 속도(ẋ)와 위치(x)가 필요하다. 속도와 위치를 이용하여 각각의 힘을 계산하고, 이를 합하여 'Equations of Motion' 모듈로 전달한다. 기본적으로 운동 방정식은 Newton의 제 2법칙에 기반을 두고 있지만, 관절(joint) 및 와이어 로프에 의한 구속을 포함한 운동을 계산하기 위해 다물체계 동역학(multibody system dynamics)의 운동 방정식 이론을 사용하였다(Cha, et al., 2010a; Cha, et al., 2010b; Ha, et al., 2015). 운동 방정식에서 가속도를 계산하면 이를 수치적으로 적분하여 속도와 위치를 구한다. 적분 방법으로는 4차 Runge-Kutta 방법 또는 4차 Adams-Bashforth 방법 등이 사용될 수 있다. 여기서 계산된 위치는 가시화 모듈로 전달되어 매시간 침몰 선박 및 인양 장비의 운동을 확인해 볼 수 있다.
연구에서 개발된 물리 기반 인양 시뮬레이션 프로그램을 이용하여 침몰 선박을 인양하는 시뮬레이션을 수행하였다. 시뮬레이션을 수행하기 위해서 침몰 선박의 제원 및 사용되는 해상 크레인 모델을 정하였다. 이를 기반으로 인양 방법을 설계하였고, 해저 저질의 종류와 조류의 속도에 따른 인양력의 변화를 분석하였다.
(1) 침몰 선박의 제원
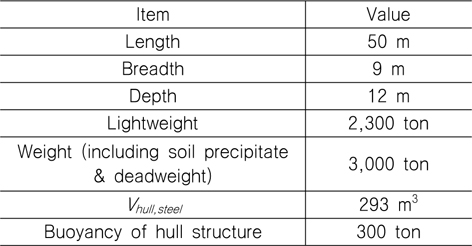
침몰 선박은 직육면체이며, 기울어짐 없이 해저 바닥에 닿았다고 가정하였다. 침몰 선박의 길이와 무게를 Table 2에 정리하였다. 여기서 침몰 선박의 중량은 침몰 선박의 경하 중량 에 재화중량과 해저 저질의 침전물 중량이 포함된 것으로 가정하였다. 선체의 강판 두께에 의한 부력은 침몰 선박의 자체 중량을 강의 밀도인 7.85 톤/m3으로 나누어 Vhull,steel을 계산하고, 여기에 해수의 밀도를 곱하여 계산하였다.
[Table 2] Principal particulars of the wreck for salvage simulation
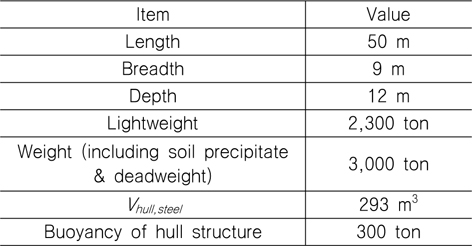
Principal particulars of the wreck for salvage simulation
(2) 인양 방법 및 장비 배치
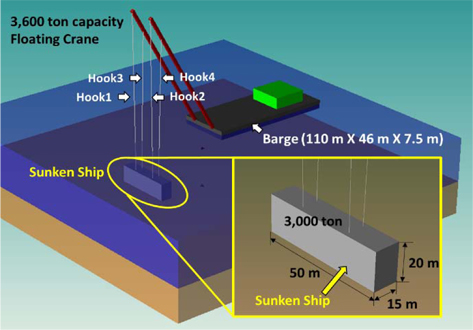
침몰 선박의 중량이 3,000톤이고, 선체의 강판 두께에 의한 부력이 300톤이므로, 리프팅에 필요한 중량은 총 2,700톤이 된다. 따라서 3,600톤급 해상 크레인을 이용하여 침몰 선박의 4개의 지점을 해상 크레인의 4개의 후크(hook)와 각각 연결하여 들어 올리는 인양 방법을 가정하였다. 인양 방법에 따른 해상 크레인과 침몰 선박을 배치하고 해상 크레인의 후크와 침몰 선박을 연결한 그림은 Fig. 8과 같다.
(3) 해저 저질에 의한 저항력 계산
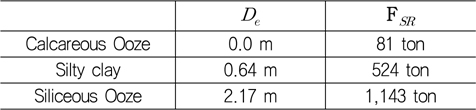
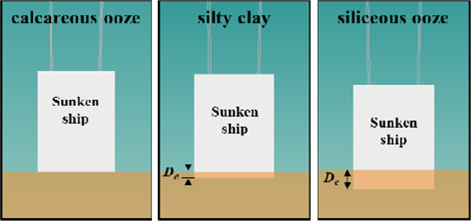
해저 저질의 종류에 따라 침몰 선박이 박히는 깊이와 저향력의 크기가 달라진다. 석회질 연니(calcareous ooze), 실트질 점토(silty clay), 규질 연니(siliceous ooze, 식물성 플랑크톤의 퇴적물)의 3가지 종류의 해저 저질에 대하여 박힌 깊이(
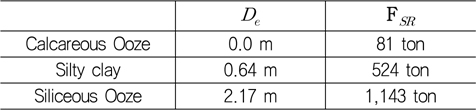
Embedment depth and soil resistance according to soil types, which are calculated by equation (8) and (9) (David & Diane, 2012)
(4) 시뮬레이션 Case의 선정
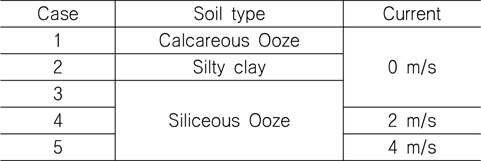
해저 저질에 의한 영향과 조류력에 의한 영향을 보기 위해 다음 5가지의 시뮬레이션 case를 선정하였다. 이 때, 조류력은 선박의 측면에 작용한다고 가정하였다.
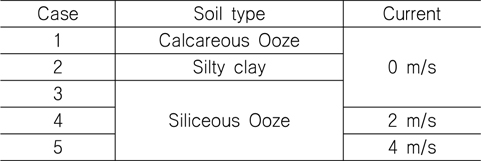
Simulation cases
본 연구에서는 Case 1, 2, 3으로부터 해저 저질의 종류에 따른 인양력의 크기와 선박의 이탈 후 수직 거동에 대해 분석하였다. 그리고 Case 3, 4, 5를 비교하여 조류의 속도에 따른 해상 크레인의 와이어 로프에 작용하는 장력을 비교하였다.
(5) 시뮬레이션 결과
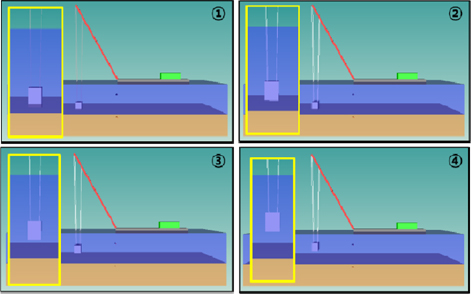
시뮬레이션 과정을 Fig. 10에 나타내었다. 시뮬레이션이 시작되면, 풀어져 있던 와이어 로프를 감기 시작한다(Fig. 10의 ① 참조). 와이어 로프에 작용하는 장력이 해저 저질에 의한 저항력보다 커지게 되면 침몰 선박이 비로소 해저면에서 이탈하여 위로 올라오게 된다(Fig. 10의 ② 참조). 해저면에서 이탈한 이후에는 지속적으로 조류력이 작용한다(Fig. 10의 ③, ④ 참조).
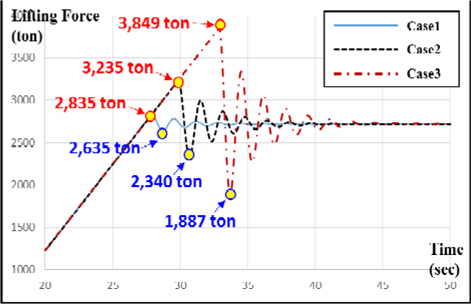
Case 1, 2, 3의 시뮬레이션 결과를 그래프로 나타내면 Fig. 11과 같다. 즉, 이 그림은 인양 과정 중 해저 저질에 따른 인양력(와이어 로프에 작용하는 장력의 변화)을 나타낸다.
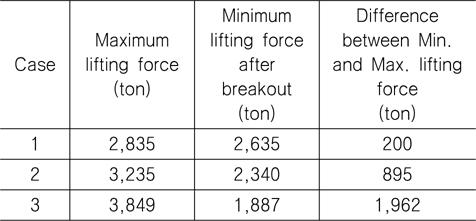
시뮬레이션 결과를 Table 5에 정리하였다. 위 시뮬레이션 결과에서 Case 3의 경우, 최대 하중으로 3,849톤이 작용함을 알 수 있다. 이 경우, 3,600톤급 해상 크레인의 허용 하중을 넘어서기 때문에 초기에 세웠던 인양 방법을 수정해야 한다. 또한 Case 3의 경우, 최대 하중(3,849톤)과 이탈 후 최소 하중(1,887톤)의 차이가 순간적으로 1,962톤(=3,849-1,887) 정도로 크게 발생하기 때문에 이로 인해 장비에 손상이 가지 않도록 주의해야 한다.
[Table 5] Simulation result: Maximum and minimum lifting forces
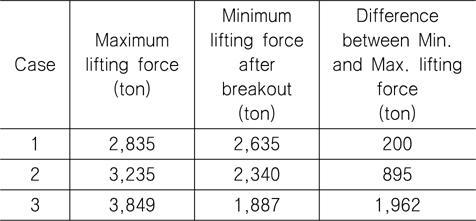
Simulation result: Maximum and minimum lifting forces
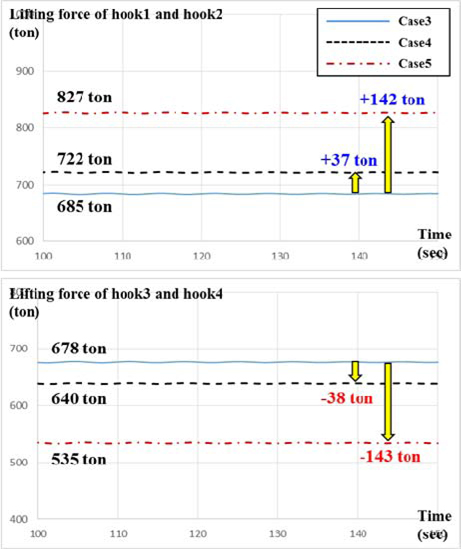
한편, 조류에 의한 영향으로 선박이 기울어지게 된다. 전체 인양력에는 큰 차이가 발생하지는 않지만, 앞 쪽에 있는 “Hook1”과 “Hook2”에 작용하는 하중이 증가하고, “Hook3”과 “Hook4”에 작용하는 하중은 감소한다. 이를 그래프로 나타내면 Fig. 12와 같다.
본 연구에서는 침몰 선박의 시뮬레이션을 수행하였다. 인양 중 발생하는 환경 하중을 계산하기 위해 침몰 선박의 중량과 부력, 해저 저질에 의한 저항력, 조류력 등을 고려하였다. 이를 기반으로 시간 영역에서 해상 크레인과 같은 인양 장비에 작용하는 동적 하중을 계산하였다. 본 연구에서 개발한 프로그램의 효용성을 검증하기 위해 대상과 인양 방법을 정의하였고, 해저 저질의 종류와 조류의 속도를 바꿔가며 시뮬레이션을 수행하였다.
향후 연구로서, 해상 크레인이 받는 파도에 의한 외력을 추가적으로 고려하여 인양 중 발생하는 동적 거동을 보다 정확하게 예측하고자 한다. 이를 위해서는 Cummins 식 (Cummins, 1962)기반의 시간 영역에서의 유체 동역학 해석 모듈을 추가로 구현해야 한다. 또한 본 프로그램을 다양한 인양 방법에 적용해 봄으로써 그 효용성을 제고할 계획이다.