Localization of a sensor network node using machine learning has been recently studied. It is easy for Support vector machines algorithm to implement in high level language enabling parallelism. Raspberrypi is a linux system which can be used as a sensor node. Pi can be used to construct IP based Hadoop clusters. In this paper, we realized Support vector machine using python language and built a sensor network cluster with 5 Pi’s. We also established a Hadoop software framework to employ MapReduce mechanism. In our experiment, we implemented the test sensor network with a variety of parameters and examined based on proficiency, resource evaluation, and processing time. The experimentation showed that with more execution power and memory volume, Pi could be appropriate for a member node of the cluster, accomplishing precise classification for sensor localization using machine learning.
무선통신, 저전력 회로, 반도체 미세 공정의 발달로 인해 차세대 무선 센서 네트워크에 대한 연구는 하나의 독립적인 연구분야로 자리잡고 있다. 무선 센서 노드는 군사 분계 지역의 탐색, 산업 공장의 기기간 통신 등 다양한 분야에 적용하여 임무 수행이 가능하다[1].
센서 노드의 위치 측정(localization)은 네트워크는 물론 어플리케이션 도메인에서의 위치 정보를 확보한다는 것을 의미한다. 센서 노드의 정확한 위치의 파악은 네트워크의 에너지 감지형 어드레싱, 위치 측정, 데이터 소집에 필수적이다. 하지만, 센서 노드의 개수가 점차 늘어가는 경향에서 수백, 수천개의 센서 노드에 대한 수동 위치 파악은 거의 불가능하다. 무선 센서 네트워크를 위한 기존 위치 측정 방법들은 유클리드의 삼각법을 사용하며 센서 네트워크의 특성을 분석하여 노드의 위치를 파악한다[2].
센서 노드의 위치를 파악하는 새로운 방식은 기계학습 [3]에 근거한다. 센서 노드의 위치를 파악하는 데 적용이 가능한 두 종류의 알려진 기계학습 알고리즘은 분류 (classification)에 의한 방법과 회귀 (regression)에 의한 방법이다. 분류에 의한 방법에는 k-nearest neighbors, naive Bayes, 지지벡터머신 (support vector machines; SVM), 결정 트리 등이 있고[4-6], 회귀에 의한 방법은 선형 회귀, 지역별 차등적 선형 회귀, ridge, lasso 등이 있다[7-10]. Nguyen은 센서 노드의 위치파악이 분류에 의한 방법으로 모델될 수 있다고 밝혔다[11]. 분류에 의한 방법 중, 지지벡터머신은 낮은 일반화의 에러율, 상대적으로 낮은 계산처리비용, 이분법에 의한 데이터 분석의 단순화라는 특성을 가진다.
무선 센서 네트워크의 통신 프로토콜은 블루투스, ZigBee, RFID, ZWave 등 단순한 통신 프로토콜을 사용하는 것이 추세였지만, 최근 라즈베리파이와 같은 신용카드 크기의 초소형 컴퓨터 시스템의 등장으로 인해 로우엔드 컴퓨터 시스템을 센서 노드로 하고 인터넷 프로토콜을 사용한 통신 프로토콜을 사용함으로써 하둡과 같은 분산 컴퓨팅 기술이 사용 가능해졌다. 본 논문에서는 로우엔드 센서로 라즈베리파이에 센서를 장착하여 사용하고, 하둡 클러스터를 제작하여 센서 노드 위치 측정에 적용 가능한 지지벡터머신 알고리즘을 구현하고 성능을 분석하려 한다.
Ⅱ. 지지 벡터 머신(Support Vector Machines)
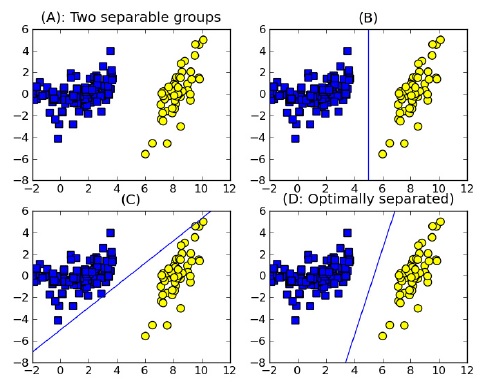
기계 학습을 이용한 노드 위치 측정 문제는 결정 가능한 범위 내에서 데이터 포인트가 기준점으로부터 얼마나 떨어져 있는지를 판단하여 이분법적인 결정을 내릴 수 있는 신뢰도가 높은 분류기를 필요로 한다. 그림 1에서 동일한 분포를 보이는 데이터 표본에 대하여 데이터를 서로 다른 두 그룹으로 나눌 수 있는 여러 가지 방법을 보인다. 데이터가 2차원으로 흩어져 있어, 이들을 두 그룹으로 나누기 위해서는 최적으로 분할해주는 1차원 직선이 필요하다. 그림에서는 (D)가 최적이라고 보여지며, 이러한 벡터를 지지 벡터라고 하며 우리는 기계학습을 이용하여 지지 벡터를 효율적으로 구하고자 한다.
2.2. 지지 벡터를 위한 Pegasos (Primal Estimated sub-GrAdient SOlver for Svm) 알고리즘
본 논문에서는, 모든 센서 노드에 대한 위치 측정을 위해 분산 컴퓨팅의 개념을 도입하였다. 지지 벡터를 구하는 데 있어 기존에 가장 많이 사용되어 오고 있는 순차 최소 최적화 (SMO; sequential minimal optimization)는 기본적으로 순차적인 방식이어서 데이터의 개수가 많아질수록 연산 속도가 급속히 감소한다. 만일 SMO의 큰 작업을 작은 부분으로 분할하는 것이 가능하다면, 이에 맵리듀스 [12] 방식을 적용하여 분산 처리가 가능하다. Pegasos 알고리즘은 SMO에 대한 대안으로 사용이 가능하며, 지지 벡터를 구하는 데 병렬성을 도입할 수 있다.Pegasos에서는 훈련 데이터에서 임의로 선택한 집합이 그룹에 더해지며, 검사를 진행한다. 만일 잘 분류가 되었다면 무시하고 진행하고, 잘 안되었다면 해당 집합을 새로운 집합에 더한다. 작업이 끝나면 가중벡터 w를 잘 분류되지 않았던 데이터의 정보로 갱신하며 이러한 작업은 반복적으로 수행되어 최종적으로 지지 벡터를 얻게 된다. 본 논문에서는 라즈베리파이 [13] Hadoop 클러스터를 활용하기 위해 Pegasos를 python으로 구현하였다. python은 mrjob이라는 라이브러리를 지원하여 분산 프로그래밍이 가능하다. Pegasos에 대한 의사코드를 그림 2에 보인다[14]. 본 논문에서는 그림 2의 알고리즘을 python 프로그램으로 구현하여 [14]의 결과와 비교하여 신뢰성을 확보하였다.
실험 환경을 구축하기 위해, 우리는 mrjob 구조를 사용한 Pegasos 알고리즘을 python 프로그램으로 구현하였다. 맨 먼저, 병렬로 구현이 가능한 부분과 가능하지 않은 부분을 찾아 Pegasos 알고리즘을 Map 단계와 Reduce 단계로 나누었다.
실제 코드를 작성하여 동작하는 코드를 조사하고 실행되는 프로세스를 살펴본 결과 대부분의 시간이 알고리즘 내에서 동작하는 부분에서 소모된다는 것을 파악하였고, 가중치 벡터 w의 축적은 병렬로 처리되지 못한다는 것을 파악하였다. 그래서 또다른 python 라이브러리 중 하나인 pickle을 사용하고 두 개의 반복횟수와 그룹의 크기를 저장하는 새로운 변수를 사용하였다. 또한 mrjob이 어떻게 어떤 순서로 작업을 처리할 것인지를 결정하는 python method과 입출력을 그림 3과 같이 제안하였다. 그림 3에서 보이듯 이 방법은 mapper, mapper_final, reducer 스테이지로 나누어 list로 만들고 반복적으로 조작한다. 정확한 동작을 위해서, mapper는 reducer의 시간에 맞는 결과값을 알 수 있어야 한다.
첫 번째 method인 mapper()는 분산 프로세싱을 처리하기 위한 것이다. 이는 mapper_final() method가 요구하는 값들을 순서대로 정렬한다. 입력 타입으로는 가중치 벡터, 반복 회수, 인덱스 값을 받는다. 변수의 상태를저장하는 것이 불가능하기 때문에, 빠르고 쉬운 전달을 위해서 키/값의 형태로 디스크에 저장하는 방식을 택하였다.
두 번째 method인 mapper_final()은 매번 입력 값들이 결정될때마다 동작한다. 이 때 가중치 벡터 w과 인덱스 값 정수 타입 x를 얻게 된다. mapper_final()이 시작하면, 데이터는 라벨과 원시 데이터로 그룹핑 된다. 만일 잘못 분류된 데이터가 존재하는 경우, 그 데이터는 reducer()로 전송된다. 이 때, w와 t의 값이 같이 전달되어 mapper()와 reducer()간의 상태를 조절한다.
마지막 method인 reducer()는 모든 키/값을 반복적으로 판별하여 지역 변수에 전달한다. 프로그램에서 가중치 벡터 w를 갱신하고 지지 벡터 알고리즘의 eta를 결정하기 위해 몇 가지 변수를 더 추가하였다. 새로운 임의의 벡터 그룹이 선택되고 전달되면 값의 키들은 mapper()의 결과가 된다.
라즈베리파이를 사용한 하둡 분산 환경을 구축하기 위해 그림 4와 같이 구성하였다. 실험적으로 5개의 라즈베리파이 노드, 유선랜, 무선랜, 센서, 전력 공급을 위한 유전원 허브를 사용하였다. 실험으로는 유선랜을 사용하였다. 하지만, 각 센서 노드에는 USB 포트가 있어 실제 배치할 때는 무선랜의 사용이 가능하다.
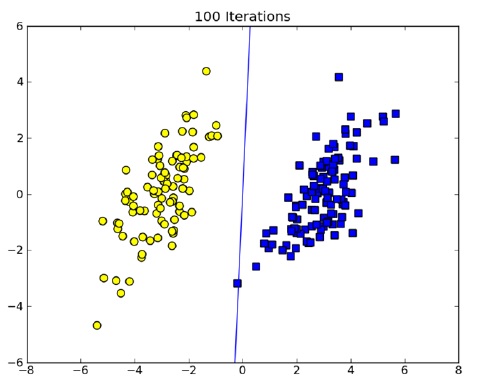
이제 그림 4와 같이 테스트 벤치를 구성하여 성능 평가를 수행할 준비가 되었다. 이 플랫폼을 기준으로 클러스터 노드의 개수를 변화시키면서 마스터와 슬레이브 간의 로드 밸런싱을 측정하였다. 클러스터 노드의 개수를 2개에서 5개까지 변화시켜가면서 Pegasos의 맵 리듀스 버전을 실행하였다. 각 100회 반복 이후, 그림 5와 같은 초평면 위의 동일한 데이터그램을 얻을 수 있었다. 10000개의 샘플 데이터를 입력하였고 반복 회수를 50에서 100까지 변화시켜도 큰 차이를 보이지 않으며 한 개의 데이터 샘플을 제외하고는 모두 안정적인 분류를 수행하였다.
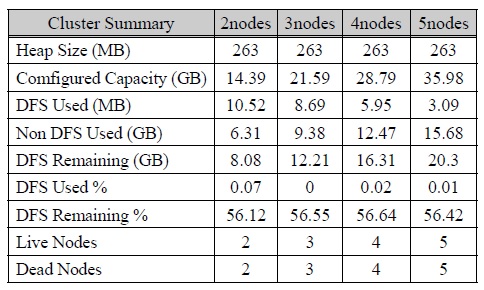
실험을 수행할 시 가장 중요하게 고려했던 부분은 효율성, 자원 분배, 테스트로 수행한 분산 Pegasos 프로그램 수행 시간이었다. 표 1은 하둡 프레임워크가 수행한 클러스터 자원의 할당량을 정리한 것이다. 하나의 클러스터 노드가 디스크로 8GiB SD카드를 사용하기 때문에, 표 1에 보이는 저장장치 용량은 노드가 더해질수록 커진다.
[표 1.] 클러스터 노드의 개수에 따른 라즈베리파이 하둡 클러스터의 종류별 저장용량의 변화
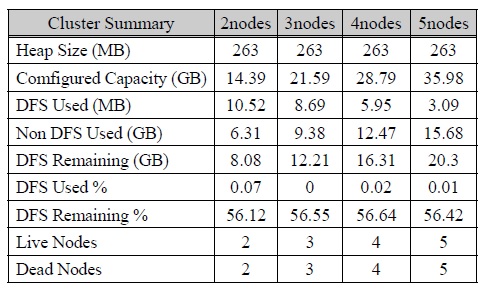
클러스터 노드의 개수에 따른 라즈베리파이 하둡 클러스터의 종류별 저장용량의 변화
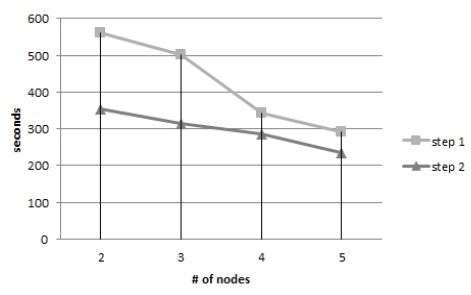
저장용량의 변화 분석 이후, 우리는 마찬가지로 노드의 개수를 변화시켜가면서 python으로 구현한 Pegasos 알고리즘의 수행 속도를 측정하였다. 알고리즘은 맵/리듀스의 두 단계로 진행되었고, 실제 측정한 시간은 각 단계에서 수행된 시간을 합한 것이다. 예측한대로, 노드의 개수가 많을수록 (5개) 수행속도에 대한 이득을 얻는 것을 볼 수 있다. (그림 6)
하둡 클러스터는 노드 이름을 관리하는 name node와 secondary name node, 노드작업을 관리하는 job tracker를 반드시 필요로 하며, 이는 시스템 관리자가 어떻게 구성하느냐에 따라 처리 효율성이 달라지게 된다.
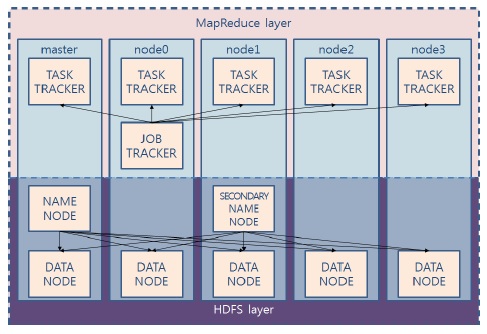
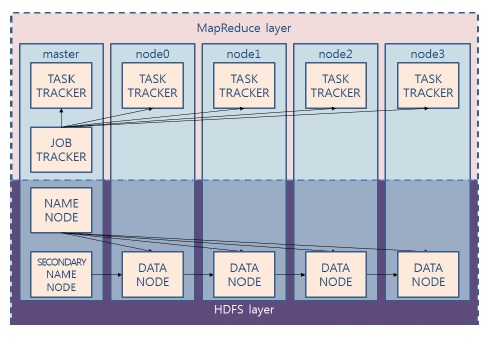
본 논문의 실험에서 클러스터 노드의 개수가 최대로 늘어났을 때, (5 개) 하둡 프레임워크는 두 가지 방식으로 구성할 수 있다. 하둡의 복잡한 서버 역할을 수행하기 위한 분산된 마스터 구성 (그림 7)과 중앙 집중된 마스터 구성 (그림 8)이다. 분산 마스터 구성은 5개의 노드를 모두 데이터 노드로 사용하였고, 중앙 집중형 마스터 구성에서는 4 개의 노드만을 데이터 노드로 구성하였다. 노드의 개수가 적어 하둡 분산 처리를 수행하는 데 큰 차이가 나지 않는다고 생각할 수 있으나, 리눅스 명령어 time을 사용하여 전체 수행시간을 조사한 결과 분산 마스터 구성 방식이 약 120초만큼 더 빨리 수행하였다. 이는 하둡 시스템이 맵리듀스 작업을 준비하느라 소비되는 초기 시작 작업의 특성에 기인하는 것으로 분석된다.
분석 대상 데이터의 규모가 크지 않다면 하둡 클러스터는 좋은 선택이 아닐 것이다. 분산 시스템 환경에서는 맵핑, 병렬화, 리듀싱이 항상 컴퓨팅 파워를 소비하기 때문에 기회비용과 분산 오버헤드가 가장 중요한 설계 고려 요소 중 하나가 된다.
본 논문에서는 초소형 컴퓨터 시스템인 라즈베리파이를 센서 노드로 사용하여 클러스터 플랫폼을 구성하고, 순차적인 SMO 알고리즘을 분산 프로그래밍을 지원하도록 변형하여 기계 학습에 의한 센서 노드 위치 측정을 위한 분산 지지 벡터 머신을 구현하였다. 또한,라즈베리파이를 지지 벡터 머신 용용 센서 노드로 활용하는 것이 적절한지에 대한 분석도 수행하였다. 분산 하둡 클러스터의 센서 노드로 라즈베리파이는 컴퓨팅 파워와 메모리 면에서는 부족한 점을 보여 시간은 비교적 많이 소모하였으나, 정확한 결과를 산출하여 실시간 결과가 필요하지 않은 응용에는 적절히 사용될 수 있을 것으로 기대된다.