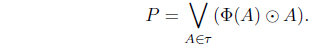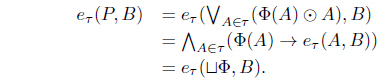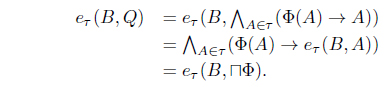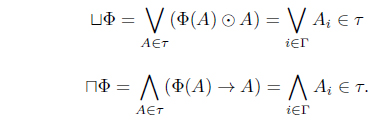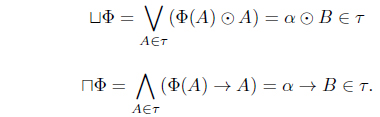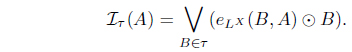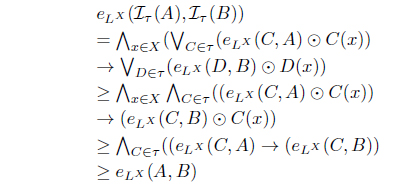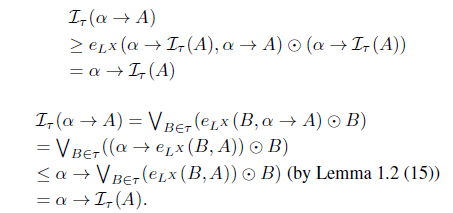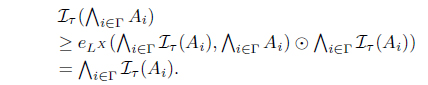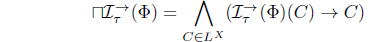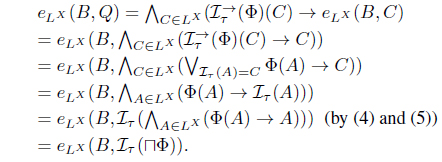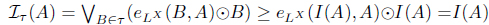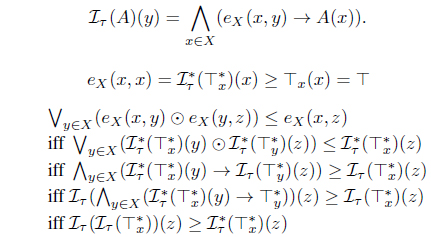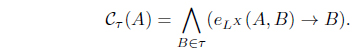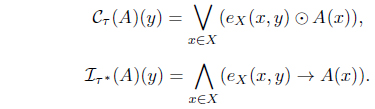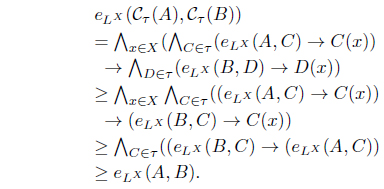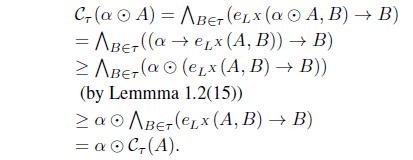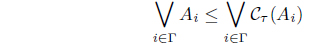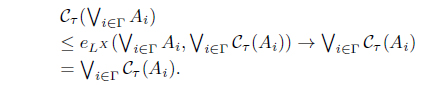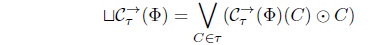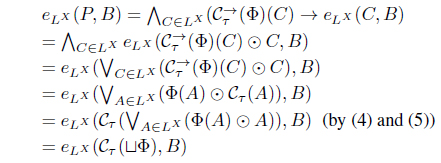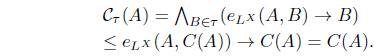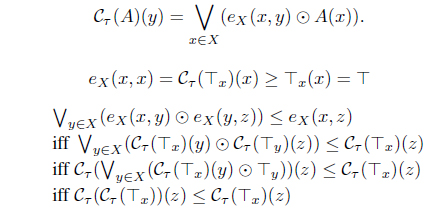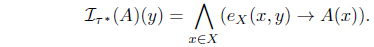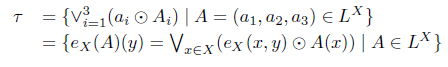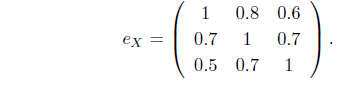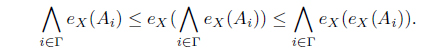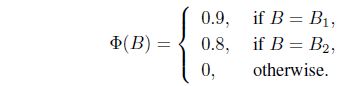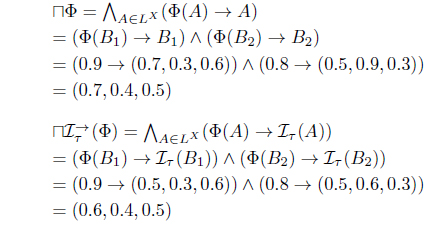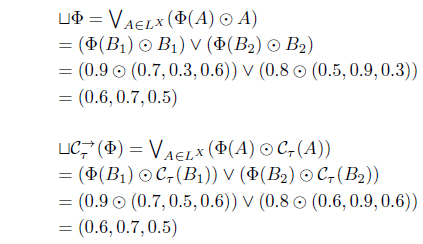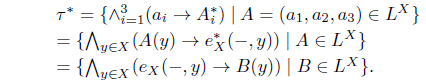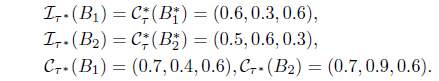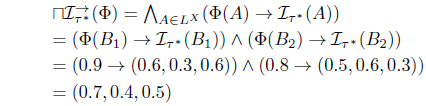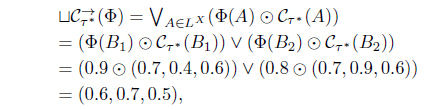Some Properties of Alexandrov Topologies

Kim
Yong Chan; Kim
Young Sun

doi:10.5391/IJFIS.2015.15.1.72

OA학술지
International Journal of Fuzzy Logic and Intelligent Systems

Some Properties of Alexandrov Topologies

DOI : 10.5391/IJFIS.2015.15.1.72
Author: Kim Yong Chan, Kim Young Sun
Publish: International Journal of Fuzzy Logic and Intelligent Systems Volume 15, Issue1, p72~78, 25 March 2015

ABSTRACT

Alexandrov topologies are the topologies induced by relations. This paper addresses the properties of Alexandrov topologies as the extensions of strong topologies and strong cotopologies in complete residuated lattices. With the concepts of Zhang’s completeness, the notions are discussed as extensions of interior and closure operators in a sense as Pawlak’s the rough set theory. It is shown that interior operators are meet preserving maps and closure operators are join preserving maps in the perspective of Zhang’s definition.

KEYWORD

Complete residuated lattices , Alexandrov topologies , Fuzzy partially ordered set , Meet and join

본문

Collapse all

1. Introduction

Pawlak [1, 2] introduced the rough set theory as a formal tool to deal with imprecision and uncertainty in the data analysis. Hájek [3] introduced a complete residuated lattice which is an algebraic structure for many valued logic. By using the concepts of lower and upper approximation operators, information systems and decision rules are investigated in complete residuated lattices [3-7]. Zhang and Fan [8] and Zhang et al. [9] introduced the fuzzy complete lattice which is defined by join and meet on fuzzy partially ordered sets. Alexandrov topologies [7, 10-12] were introduced the extensions of fuzzy topology and strong topology [13].

In this paper, we investigate the properties of Alexandrov topologies as the extensions of strong topologies and strong cotopologies in complete residuated lattices. Moreover, we study the notions as extensions of interior and closure operators. We give their examples.

Definition 1.1. [3, 4] An algebra (L, ∧, ∨, ⊙, →, ⊥, 𝖳) is called a complete residuated lattice if it satisfies the following conditions:

(C1) L = (L, ≤, ∨, ∧, ⊥, 𝖳) is a complete lattice with the greatest element 𝖳 and the least element ⊥; (C2) (L, ⊙, 𝖳) is a commutative monoid; (C3) x ⊙ y ≤ z iff x ≤ y → z for x, y, z ∈ L.

In this paper, we assume (L, ∧, ∨, ⊙, →, ^∗ ⊥, 𝖳) is a complete residuated lattice with a negation; i.e., x^∗∗ = x. For α ∈ L, A, 𝖳_x ∈ L ^X, (α → A)(x) = α → A(x), (α ⊙A)(x) = α ⊙ A(x) and 𝖳_x(x) = 𝖳, 𝖳_x(x) = ⊥, otherwise.

Lemma 1.2. [3, 4] For each x, y, z, x_i , y_i ∈ L, the following properties hold.

(1) If y ≤ z, then x ⊙ y ≤ x ⊙ z. (2) If y ≤ z, then x → y ≤ x → z and z → x ≤ y → x. (3) x → y = 𝖳 iff x ≤ y. (4) x → 𝖳 = 𝖳 and 𝖳 → x = x. (5) x ⊙ y ≤ x ∧ y. (6). (7) and . (8) and . (9) (x → y) ⊙ x ≤ y and (y → z) ⊙ (x → y) ≤ (x → z). (10) x → y ≤ (y → z) → (x → z) and x → y ≤ (z → x) → (z → y). (11) and . (12) (x ⊙ y) → z = x → (y → z) = y → (x → z) and (x ⊙ y)∗ = x → y∗. (13) x∗ → y∗ = y → x and (x → y)∗ = x ⊙ y∗. (14) y → z ≤ x ⊙ y → x ⊙ z. (15) x → y ⊙ z ≥ (x → y) ⊙ z and (x → y) → z ≥ x ⊙ (y → z).

Definition 1.3. [7, 10, 12, 13] A subset τ ⊂ L ^X is called an Alexandrov topology if it satisfies:

(T1) ⊥X, 𝖳X ∈ τ where 𝖳X(x) = 𝖳 and ⊥X(x) = ⊥ for x ∈ X. (T2) If Ai ∈ τ for i ∈ Γ, . (T3) α ⊙ A ∈ τ for all α ∈ L and A ∈ τ. (T4) α → A ∈ τ for all α ∈ L and A ∈ τ.

A subset τ ⊂ L^X satisfying (T1), (T3) and (T4) is called a strong topology if it satisfies:

(ST) If A_i ∈ τ for i ∈ Γ, for each finite index Λ ⊂ Γ.

A subset τ ⊂ L^X satisfying (T1), (T3) and (T4) is called a strong cotopology if it satisfies:

(SC) If A_i ∈ τ for i ∈ Γ, for each finite index Λ ⊂ Γ.

Remark 1.4. Each Alexandrov topology is both strong topology and strong cotopology.

Definition 1.5. [8, 9] Let X be a set. A function e_X : X×X → L is called:

(E1) reflexive if eX (x, x) = 𝖳 for all x ∈ X, (E2) transitive if eX(x, y) ⊙ eX(y, z) ≤ eX(x, z), for all x, y, z ∈ X, (E3) if eX(x, y) = eX(y, x) = 𝖳, then x = y.

If e satisfies (E1) and (E2), (X, e_X) is a fuzzy preordered set. If e satisfies (E1), (E2) and (E3), (X, e_X) is a fuzzy partially ordered set.

Example 1.6. (1) We define a function e_L^X : L ^X × L ^X → L as . Then (L ^X, e_L^X ) is a fuzzy partially ordered set from Lemma 1.2 (8).

(2) Let τ be an Alexandrov topology. We define a function e_τ : τ × τ → . Then (τ, e_τ ) is a fuzzy partially ordered set.

Definition 1.7. [8, 9] Let (X, e_X) be a fuzzy partially ordered set and A ∈ L^X.

(1) A point x0 is called a join of A, denoted by x0 = ⊔A if it satisfies (J1) A(x) ≤ eX(x, x0), (J2) . A point x1 is called a meet of A, denoted by x1 = ⊓A, if it satisfies (M1) A(x) ≤ eX(x1, x), (M2) .

Remark 1.8. [8, 9] Let (X, e_X) be a fuzzy partially ordered set and A ∈ L^X.

(1) x0 is a join of A iff. (2) x1 is a meet of A iff . (3) If x0 is a join of A, then it is unique because eX(x0, y) = eX(y0, y) for all y ∈ X, put y = x0 or y = y0, then eX(x0, y0) = eX(y0, x0) = 𝖳 implies x0 = y0. Similarly, if a meet of A exist, then it is unique.

Remark 1.9. [8, 9] Let (L ^X, e_L^X ) be a fuzzy partially ordered and Φ ∈ L^{L^X}.

(1) Since then .(2) We have because

2. Some Properties of Alexandrov Topologies

Theorem 2.1. (1) A subset τ ⊂ L^X is an Alexandrov topology on X iff for each Φ : τ → L, ⊔Φ ∈ τ and ⊓Φ ∈ τ.

(2) τ is an Alexandrov topology on X iff τ^∗ = {A^∗ ∈ L^X | A ∈ τ} is an Alexandrov topology on X.

Proof. (1) (⇒) For each Φ : τ → L, we define

Since τ is an Alexandrov topology on X, (Φ(A) ⊙ A) ∈ τ . Thus P ∈ τ . Then P = ⊔Φ from:

For each Φ : τ → L, we define . Since τ is an Alexandrov topology on X, (Φ(A) → A) ∈ τ. Thus Q ∈ τ. Then Q = ⊓Φ from:

(⇒) (T1) For Φ(A) = ⊥ for all A ∈ τ , and .

(T2) Let Φ(A_i) = 𝖳 for all {A_i | i ∈ Γ} ⊂ τ , otherwise Φ(A) = ⊥. We have

(T3) Let Φ(A) = ⊥ for A = B ∈ τ , otherwise Φ(A) = α if A ≠ B. We have

(2) Let A^∗ ∈ τ^∗ for A ∈ τ . Since α ⊙ A^∗ = (α → A)^∗ and α → A^∗ = (α⊙A)^∗, τ^∗ is an Alexandrov topology on X.

Theorem 2.2. Let τ be an Alexandrov topology on X. Define I_τ : L^X → L^X as follows:

Then the following properties hold.

(1) eLX (A, B) ≤ eLX (Iτ (A), Iτ (B)), for A, B ∈ LX. (2) Iτ (A) ≤ A for all A ∈ LX. (3) Iτ (Iτ (A)) = Iτ (A) for all A ∈ LX. (4) Iτ (α → A) = α → Iτ (A) for all α ∈ L, A ∈ LX. (5) for all Ai ∈ LX. (6) for each Φ : L X → L where defined as . (7) . (8) Define τIτ = {A | A = Iτ (A)}. Then τ = τIτ . (9) There exists a fuzzy preorder eX : X × X → L such that

Proof. (1) By Lemma 1.2 (8,10,14), we have

(2) Since e_L^X (C, A)⊙C ≤ A from Lemma 1.2 (9), I_τ (A) ≤ A.

(3) Since I_τ (A) ∈ τ , then

I_τ (I_τ (A)) ≥ e_L^X (I_τ (A), I_τ (A)) ⊙ I_τ (A) = I_τ (A).

By (2), I_τ (I_τ (A)) = I_τ (A).

(4) Since α → I_τ (A) ≤ α → A and α → I_τ (A) ∈ τ ,

(5) By (1), since I_τ (A) ≤ I_τ (B) for . Since and , we have

(6) For each Φ : L^X → L, put . Since is a map, we have

and from:

(7) . Since I(A) ≤ A and I(A) ∈ τ , we have

Since I_τ (A) ≤ A and I_τ (A) ∈ τ , we have I(A) ≥ I_τ (A).

(8) It follows from A ∈ τ iff I_τ (A) = A iff A ∈ τ_{I_τ}.

(9) Since , by (4) and (5), . Put . Then

Hence e_X is a fuzzy preorder.

Theorem 2.3. Let τ be an Alexandrov topology on X. Define C_τ : L^X → L^X as follows:

Then the following properties hold.

(1) eLX (A, B) ≤ eLX (Cτ (A), Cτ (B)), for all A, B ∈ LX. (2) A ≤ Cτ (A) for all A ∈ LX. (3) Cτ (Cτ (A)) = Cτ (A) for all A ∈ LX. (4) Cτ (α ⊙ A) = α ⊙ Cτ (A) for all α ∈ L, A ∈ LX. (5) for all Ai ∈ LX. (6) for each Φ : LX → L where defined as . (7) . (8) Define τCτ = {A | A = Cτ (A)}. Then τ = τCτ. (9) (Cτ (A∗))∗ = Iτ∗ (A) for all A ∈ LX. (10) There exists a fuzzy preorder eX : X × X → L such that

Proof. (1) By Lemma 1.2 (8,10), we have

(2) Since e_L^X (A, B) ⊙ A ≤ B iff A ≤ e_L^X (A, B) → B , then A ≤ C_τ (A).

(3) Since C_τ (A) ∈ τ , then C_τ (C_τ (A)) ≤ e_L^X (C_τ (A), C_τ (A)) → C_τ (A) = C_τ (A). By (2), C_τ (C_τ (A)) = C_τ (A).

(4) Since α ⊙ A ≤ α ⊙ C_τ (A) and α ⊙ C_τ (A) ∈ τ ,

C_τ (α ⊙ A) ≤ e_L^X (α ⊙ A, α ⊙ C_τ (A)) → α ⊙ C_τ (A) = α ⊙ C_τ (A).

(5) By (1), since C_τ (A) ≤ C_τ (B) for A ≤ B, . Since

and

we have

(6) For each Φ : L^X → L, put . Since is a map, we have

and from:

(7) Put . Since A ≤ C(A) and C(A) ∈ τ , we have

Since A ≤ C_τ (A) and C_τ (A) ∈ τ , we have C(A) ≤ C_τ (A).

(8) It follows from A ∈ τ iff C_τ (A) = A iff A ∈ τ_{C_τ}.

(9)

(10) Since , by (4) and (5), . Put e_X(x, y) = C_τ (𝖳_x)(y). Then

Hence e_X is a fuzzy preorder. Since , by Theorem 2.2(9),

Example 2.4. Let (L = [0, 1], ⊙, →,^∗ ) be a complete residuated lattice with a negation defined by

x⊙y = (x+y−1)∨0, x → y = (1−x+y)∧1, x^∗ = 1−x.

Let X = {x, y, z} be a set and A₁ = (1, 0.8, 0.6), A₂ = (0.7, 1, 0.7), A₃ = (0.5, 0.7, 1).

(1) We define

where

(T1) For ⊥_X ∈ L^X, e_X(⊥_X) = ⊥_X ∈ τ . For 𝖳_X ∈ L^X, e_X(𝖳_X) = 𝖳_X ∈ τ .

(T2) For e_X(A_i) ∈ τ for each i ∈ Γ, . Moreover, since e_X(A)(x) ≥ e_X(x, x) ⊙ A(x) = A(x) and e_X(e_X(A)) = e_X(A),

Hence .

(T3) For e_X(A) ∈ τ , α ⊙ e_X(A) = e_X(α ⊙ A) ∈ τ.

(T4) Since α ⊙ e_X(α → e_X(A)) ≤ e_X(e_X(A)) = e_X(A), we have

α → e_X(A) ≤ e_X(α → e_X(A)) ≤ α → e_X(A)

Hence, for e_X(A) ∈ τ , α → e_X(A) = e_X(α → e_X(A)) ∈ τ . Hence τ is an Alexandrov topology on X.

(2) For B₁ = (0.7, 0.3, 0.6), B₁ = (0.5, 0.9, 0.3), we obtain

Iτ (B1) = (0.5, 0.3, 0.6), Iτ (B2) = (0.5, 0.6, 0.3), Cτ (B1) = (0.7, 0.5, 0.6), Cτ (B2) = (0.6, 0.9, 0.6).

Let Φ : L^X → L as follows

Thus, .

Thus, .

(3) We define

For B₁, B₂ and Φ in (2), we obtain

Since ⊓Φ = (0.7, 0.4, 0.5) and

we have .

Since ⊔Φ = (0.6, 0.7, 0.5) and

then .

3. Conclusions

The fuzzy complete lattice is defined with join and meet operators on fuzzy partially ordered sets. Alexandrov topologies are the extensions of fuzzy topology and strong topology.

Several properties of join and meet operators induced by Alexandrov topologies in complete residuated lattices have been elicited and proved. In addition, with the concepts of Zhang’s completeness, some extensions of interior and closure operators are investigated in the sense of Pawlak’s rough set theory on complete residuated lattices. It is expected to find some interesting functorial relationships between Alexandrov topologies and two operators.

참고문헌

1. Pawlak Z. 1982 “Rough sets,” [International Journal of Computer & Information Sciences] Vol.11 P.341-356
2. Pawlak Z. 1984 “Rough probability,” [Bulletin of the Polish Academy of Sciences Mathematics] Vol.32 P.607-615
3. Hajek P. 1998 Metamathematics of Fuzzy Logic
4. B？olhlaek R. 2002 Fuzzy Relational Systems: Foundations and Principles
5. Radzikowska A. M., Kerre E. E. 2002 “A comparative study of fuzzy rough sets,” [Fuzzy Sets and Systems] Vol.126 P.137-155
6. She Y. H., Wang G. J. 2009 “An axiomatic approach of fuzzy rough sets based on residuated lattices,” [Computers & Mathematics with Applications] Vol.58 P.189-201
7. Ma Z.M., Hu B. Q. 2013 “Topological and lattice structures of L-fuzzy rough sets determined by lower and upper sets,” [Information Sciences] Vol.218 P.194-204
8. Zhang Q. Y., Fan L. 2005 “Continuity in quantitative domains,” [Fuzzy Sets and Systems] Vol.154 P.118-131
9. Zhang Q., Xie W., Fan L. 2009 “Fuzzy complete lattices,” [Fuzzy Sets and Systems] Vol.160 P.2275-2291
10. Kim Y. C. 2014 “Alexandrov L-topologies,” [International Journal of Pure and Applied Mathematics] Vol.93 P.165-179
11. Kim Y. C. 2014 “Alexandrov L-topologies and L-join meet approximation operators,” [International Journal of Pure and Applied Mathematics] Vol.91 P.113-129
12. Lai H., Zhang D. 2006 “Fuzzy preorder and fuzzy topology,” [Fuzzy Sets and Systems] Vol.157 P.1865-1885
13. Zhang D. 2007 “An enriched category approach to many valued topology,” [Fuzzy Sets and Systems] Vol.158 P.349-366

이미지 / 테이블

OA 실천선언

기관별보기

유형별보기

OA 학술지

OAK 소개

소통/참여

1. Introduction

2. Some Properties of Alexandrov Topologies

3. Conclusions

OA 실천선언

기관별보기

유형별보기

OA 학술지

OAK 소개

소통/참여

상세검색

자료유형선택

발행연도

기관선택

1. Introduction

2. Some Properties of Alexandrov Topologies

3. Conclusions

국내 기관

국외 기관