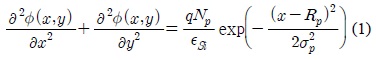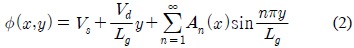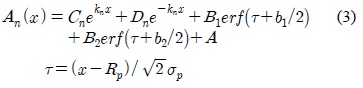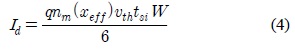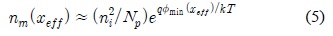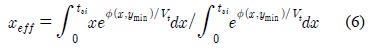반도체 소자의 미세화는 반도체 산업 발전에 가장 핵심이 되는 요소이다. 특히 집적회로에서 가장 핵심적인 역할을 담당하는 트랜지스터의 미세화는 고속 동작, 저전력소비, 집적도향상 등 반도체산업의 높은 경쟁력을 유지하기 위한 필수 요건이 되고 있다. 그러나 트랜지스터의 미세화는 단채널 효과의 증대 등 2차 효과의 발생으로 쉽게 접근할 수 없는 기술이 되고 있다. 특히 최소선폭을 10 nm이하로 제작한 CMOSFET에서 발생하는 단채널 효과는 CMOSFET를 트랜지스터로 동작하는데 제한을 가하고 있다. 즉, 문턱전압이하 스윙의 저하, 문턱전압의 이동, 드레인유기 장벽감소 현상 등 트랜지스터 동작 및 집적회로설계에 큰 방해 요소가 나타나고 있다. 이러한 방해 요소를 감소시키기 위하여 집적회로설계 기술을 개발하고 있으며 특히 3차원구조에 의한 집적도 향상에 노력하고 있다. 3차원적 설계기술의 개발뿐만이 아니라 트랜지스터의 구조도 3차원적으로 제작하기 위한 노력이 진행 중이며 이에 가장 부합된 소자가 다중 게이트 MOSFET이다[1,2]. 다중 게이트 MOSFET는 채널주변에 게이트 단자를 여러 개 제작하여 단채널 시 궁극적으로 채널길이의 증가효과 뿐만이 아니라 채널 내 반송자를 제어할 수 있는 능력을 향상시킴으로써 전술한 단채널 효과를 감소시킬 수 있다. 다중 게이트 MOSFET중에서 가장 간단한 구조가 이중 게이트 (Double Gate; DG) MOSFET이다. DGMOSFET는 상단과 하단에 게이트 단자를 제작하여 전류제어능력을 약 2배정도 향상시킬 수 있어 단채널 효과를 감소시킬 수 있다. 이러한 DGMOSFET에는 대칭형과 비대칭형이 있다[3,4]. 대칭형은 상단과 하단의 게이트를 동일단자로 하여 동일 전압을 인가시키는 3단자 소자이며 비대칭형은 상단과 하단의 게이트 구조를 달리 제작하여 각각 다른 전압을 인가할 수 있도록 제작한 4단자 소자이다. 비대칭형 DGMOSFET는 채널 내 반송자를 제어할 수 있는 설계요소가 증가하여 효과적으로 단채널 효과를 감소시킬 수 있다는 장점이 있다. 본 연구에서는 비대칭 DGMOSFET의 문턱전압이동현상에 대하여 관찰할 것이다. Ding 등[5]은 급수형태 전위분포함수를 이용하여 비대칭 DGMOSFET의 문턱전압이하 스윙을 해석하였으나 전위분포를 구하기 위하여 단지 일정한 도핑농도분포를 이용하였다. 그러나 본 연구에서는 도핑전하분포로 가우스 분포함수를 이용하였다. 가우스 분포함수는 이온주입범위 및 분포편차에 의하여 형태가 결정되는 함수로써 본 연구에서는 가우스분포함수의 변수인 이온주입범위 및 분포편차에 따른 비대칭 DGMOSFET에 대한 문턱전압 이동현상을 관찰하였다. 문턱전압은 오프상태에서 드레인 전류가 단위 폭당 0.1μA 흐를 때 상단 게이트전압으로 정의하였다[6].

2장에서는 포아송방정식의 해석학적 전위모델 및 문턱전압모델에 대하여 설명할 것이며 3장에서 이 모델을 적용하였을 경우, 문턱전압의 변화를 이온주입범위 및 분포편차에 따라 고찰하였다. 또한 4장에서 결론을 맺을 것이다.

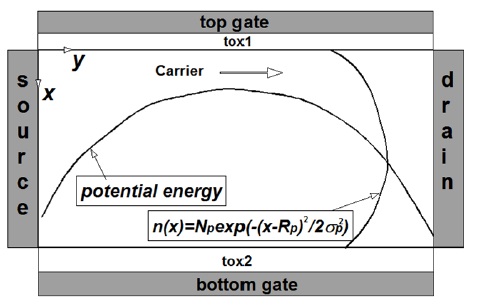
그림 1에 비대칭 DGMOSFET의 개략도를 도시하였다. 상단 게이트 단자와 하단 게이트 단자에 각각 V_gf와 V_gb의 전압을 인가할 수 있으며 상단 게이트 산화막 두께 t_ox1과 하단 게이트 산화막 두께 t_ox2를 다르게 제작 할 수 있다. 채널 내부에 도시한 도핑농도 분포함수는 가우스 분포함수를 이용하였다. 도핑농도 분포함수는 단지 x방향으로만 변화하는 일차원적 요소만을 사용하였으며 소스에서 드레인 방향으로 반송자의 이동에 영향을 미치는 열이온방출 전류가 드레인 전류를 형성할 것이다. 이와 같은 드레인 전류는 그림 1의 채널 내에 표기한 에너지장벽의 높이에 의존할 것이다. 즉, 도핑 분포함수를 이용하여 포아송방정식에서 전위분포를 구하면 문턱전압이하 영역에서 드레인 전류를 구할 수 있을 것이다.

먼저 채널 내 전위분포함수를 구하기 위하여 가우스 분포함수를 도핑분포함수로 사용하여 다음과 같이 2차원 포아송방정식을 풀었다.

여기서 ϵ_si는 실리콘의 유전율이며 N_p는 최대 도핑 분포 값, R_p와 σ_p는 각각 이온주입범위 및 분포편차를 나타낸다.

Ding 등의 경계조건을 이용하여 식 (1)을 풀면 다음과 같은 급수형태의 전위분포를 구할 수 있다[5].

이며 여기서 n은 정수, k_n = nπ/L_g이며 V_s는 소스 전압, V_d는 드레인 전압, A는 적분 상수이다. A_n(x)에 나타나는 상수 B₁,B₂,b₁,b₂,C_n,D_n는 참고문헌 [7]에 표기하였다.

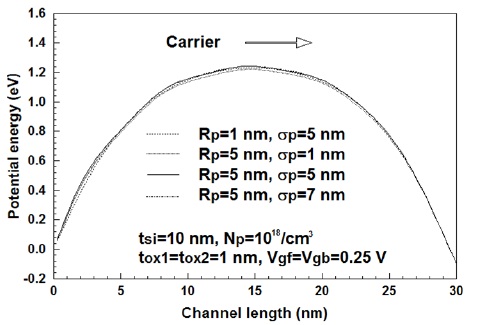
식 (2)와 식 (3)에서 알 수 있듯이 전위분포는 이온주입범위 및 분포편차에 따라 변화할 것이다. 이에 따라 변화하는 에너지장벽의 변화를 그림 2에 도시하였다. 그림 2에서 알 수 있듯이 에너지장벽의 높이는 이온주입범위 및 분포편차에 따라 변화하므로 차단전류 역시 두 요소에 따라 변화할 것이다.

본 연구에서는 차단전류가 채널 폭 당 0.1μA 일 때 상단 게이트 전압으로 문턱전압을 정의하였다. 랜덤하게 운동하는 전자들은 ±x,±y,±z의 6개 방향으로 움직일 수 있으므로 전자들의 1/6이 소스에서 드레인으로 향할 것이며 단위시간당 t_siW면적의 드레인에 도착하는 전자의 수를 이용하여 그림 2의 드레인 전류를 구하면

이다. 여기서 v_th는 열 속도이다. 전위장벽을 넘어 이동하는 캐리어의 수 n_m를 구하기 위하여 맥스웰-볼츠만 통계를 이용하였다. 식 (4)의 드레인 전류가 문턱전압의 정의에 의하여 0.1μA 일 경우, 상단 게이트 전압을 구하여 문턱전압을 얻었다. 또한 식 (4)에서 n_i는 순수반도체 전자농도이며 ϕ_min (x)는 상단게이트의 표면전위 중 최소값을 갖는 y_min 값을 구한 후, 식 (2)에 대입하며 구한 최소 전위분포 값이다. 식 (4)에서 x_eff는 전도중심으로써 식 (6)과 같이 구하여 대입한다.

이상과 같이 식 (2)의 전위분포는 이온주입범위 및 분포편차에 의하여 변화할 것이며 차단전류는 식 (4)에서 알 수 있듯이 전위분포에 따라 변화하므로 결국 차단전류는 이온주입범위 및 분포편차에 따라 변화하여 문턱전압이 영향을 받게 될 것이다. 본 연구에서는 도핑분포함수의 변수인 이온주입범위 및 분포편차에 따라 문턱전압의 변화를 고찰할 것이다.

본 연구에서 제시한 문턱전압 모델의 타당성은 참고문헌[8]에서 이미 입증하였으므로 이 모델을 사용하여 이온주입범위 및 분포편차에 대한 문턱전압의 이동현상을 고찰할 것이다.

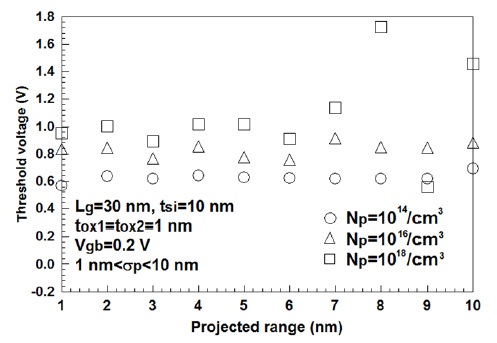
그림 3에 도핑농도를 파라미터로 구한 이온주입범위에 대한 문턱전압의 이동을 도시하였다. 분포편차가 1 nm에서 10 nm까지 변할 때의 평균값이다. 이온주입범위 및 분포편차의 효과만을 관찰하기 위하여 상·하단 산화막 두께는 1 nm로 동일하게 고정하였다. 그림 3에서 알 수 있듯이 주어진 조건에서 도핑농도가 증가하면 문턱전압이 증가하는 것을 알 수 있다. 또한 이온주입 범위가 비교적 작을 경우, 문턱전압의 변화는 그리 크지 않으나 이온주입범위가 증가할수록 문턱전압의 변화가 점점 심하게 나타나며 이러한 변화는 도핑농도가 증가할수록 더욱 심화되는 것을 관찰할 수 있다. 고 도핑상태에서는 채널 내 주입된 캐리어의 절대 수가 증가하므로 이온주입범위 및 분포편차에 따라 에너지장벽의 변화가 심해지며 이는 차단전류 및 문턱전압의 변화로 나타나고 있다는 것을 알 수 있다. 그러므로 채널이 저 도핑 상태에서는 이온주입범위 및 분포편차에 전혀 영향을 받지 않고 일정한 값을 갖는 것을 알 수 있다. 분포편차에 대한 문턱전압의 이동현상을 관찰하기 위하여 그림 4에 도핑농도를 파라미터로 한 문턱전압의 변화를 도시하였다.

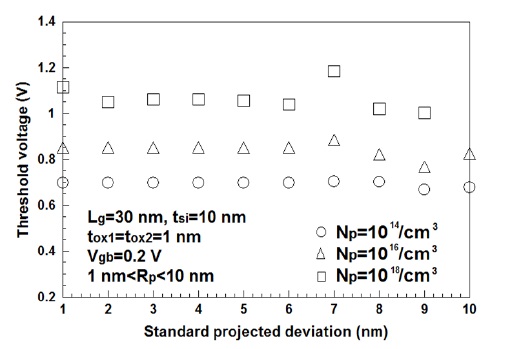
전술한 바와 같이 도핑농도가 낮을 경우, 분포편차에 따른 문턱전압의 변화는 거의 관찰되지 않는다는 것을 그림 4에서도 알 수 있다. 그러나 도핑농도가 증가하고 분포편차가 증가할수록 문턱전압의 변화는 더욱 심화되는 것을 알 수 있다. 그림 3과 비교해보면 이온주입범위나 분포편차가 증가할수록 문턱전압의 변화가 심하게 나타나며 분포편차의 증가보단 이온주입범위의 증가가 문턱전압의 변화에 더욱 큰 영향을 미치고 있다는 것을 관찰할 수 있다. 그러므로 문턱전압 이동현상을 감소시키기 위해선 가능하면 이온주입범위 및 분포편차는 작은 값을 사용하여야만 할 것이다.

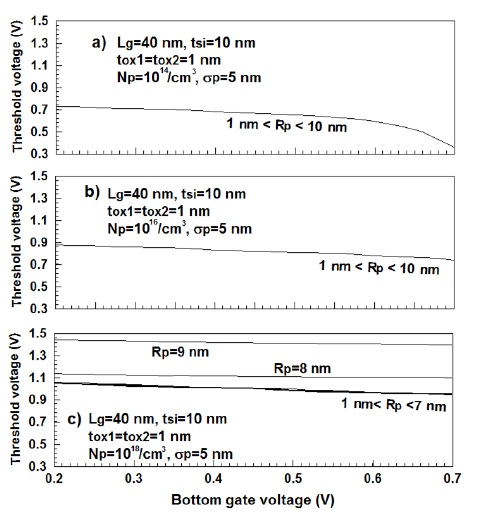
비대칭 DGMOSFET가 단채널 효과를 제어할 수 있는 또 다른 요소는 상단과 하단 게이트의 전압을 다르게 인가할 수 있다는 사실이다. 그러므로 하단 게이트 전압에 따라 전송특성에 영향을 미처 결국 문턱전압의 이동현상을 발생시킬 것이다. 이때 이온주입범위 및 분포편차에 따른 문턱전압이동현상을 관찰하기 위하여 그림 5에 하단 게이트 전압에 따른 문턱전압의 변화를 이온주입범위를 파라미터로 하여 도시하였다. 이온주입범위만의 영향을 고려하기 위하여 분포편차는 5 nm로 고정하였다. 그림 5a)와 같이 도핑농도가 낮을 경우, 전술한 바와 같이 이온주입범위에 따른 문턱전압이동 현상은 발생하고 있지 않는다는 것을 알 수 있다. 그러나 하단 게이트 전압의 증가에 따라 문턱전압은 감소하고 있었다.

그림 5b)와 같이 도핑농도가 10¹⁶/cm³정도로 증가하면 문턱전압은 약간 상승하며 하단게이트 전압의 증가에 따라 문턱전압이 선형적으로 감소하고 있다는 것을 관찰할 수 있다. 그러나 그림 5a)와 마찬가지로 이온주입범위에 따른 문턱전압의 변화는 나타나고 있지 않았다. 그림 5c)와 같이 도핑농도를 10¹⁸/cm³까지 증가시키면 이온주입범위에 따른 문턱전압의 변화가 나타나기 시작한다. 즉, 이온주입범위가 1 nm에서 7 nm까지는 이온주입범위에 따른 문턱전압의 변화가 거의 나타나고 있지 않으나 R_p = 8 nm로 상승하면 문턱전압이 증가하면서 변화를 보이고 있다. 이온주입범위가 9 nm 까지 상승하면 문턱전압은 더욱 상승하여 큰 변화를 보이고 있다. 이와 같이 고도핑된 채널을 갖는 비대칭 DGMOSFET의 경우는 이온주입범위에 따라 문턱전압이 큰 변화를 겪고 있었다. 그러나 이온주입범위가 8 nm이상에서 하단 게이트 전압에 따른 문턱전압의 변화는 거의 관찰되고 있지 않았다는 것을 주의할 필요가 있다.

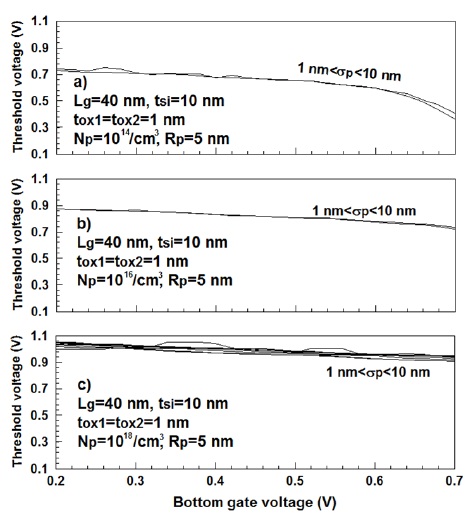
분포편차의 변화를 파라미터로 하여 하단 게이트 전압에 대한 문턱전압의 변화를 그림 6에 도시하였다. 모든 조건은 그림 5와 동일하며 이온주입범위에 대한 문턱전압의 변화 효과를 무시하기 위하여 5 nm로 고정하여 계산하였다. 도핑농도가 증가할수록 문턱전압이 증가하는 것은 그림 5에서 설명한 바와 같이 동일하다. 채널을 저 도핑 시켰을 경우, 분포편차에 따라 약간의 문턱전압변화가 발생하나 거의 일정한 분포를 보이고 있다. 저 도핑의 경우, 그림 5a)와 같이 그림 6a)에서도 하단 게이트 전압이 증가하면 문턱전압이 감소하는 경향을 보이고 있다. 도핑농도가 증가하면 문턱전압도 증가하나 분포편차에 대한 문턱전압의 변화는 관찰되고 있지 않았다. 그러나 도핑농도가 10¹⁸/cm³까지 상승하면 분포편차에 의한 문턱전압의 변화가 더욱 증가하는 추세를 보이고 있으며 하단 게이트 전압에 따라 거의 선형적으로 역 비례하는 관계를 보이고 있다.

본 연구에서는 비대칭 이중게이트 MOSFET의 채널 내 도핑분포함수의 변화를 결정하는 이온주입범위 및 분포편차에 따른 문턱전압이동 현상에 대하여 분석하였다. 도핑분포함수로 주로 사용되는 가우스분포 함수는 이온주입범위와 분포편차에 따라 그 모양을 달리하며 이는 에너지장벽의 높이 및 형태에 변화를 일으킨다. 그러므로 차단전류의 크기가 이 두 요소에 따라 변화하며 결국 문턱전압의 변화에 영향을 미치게 된다는 것을 알 수 있었다. 결과적으로 도핑농도가 증가하면 문턱전압도 증가하며 이온주입범위 및 분포편차가 클 때 문턱전압은 크게 변하였다. 특히, 하단 게이트전압이 증가할수록 저 도핑에서 이온주입범위 및 분포편차에 따른 문턱전압의 변화가 크게 나타나는 것을 알 수 있었으며 고 도핑에서 이온주입범위 및 분포편차에 따른 문턱전압의 변화가 크게 나타나는 것을 알 수 있었다.