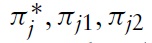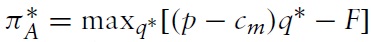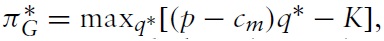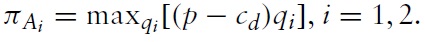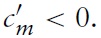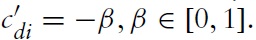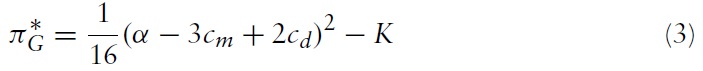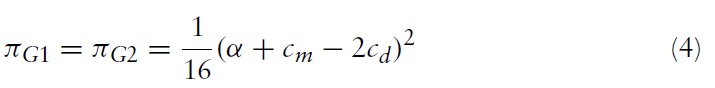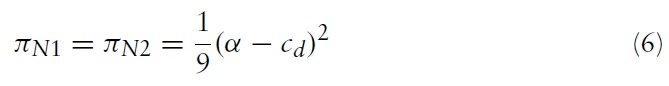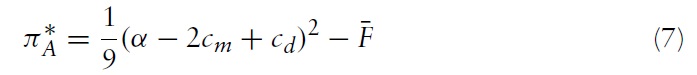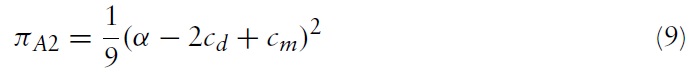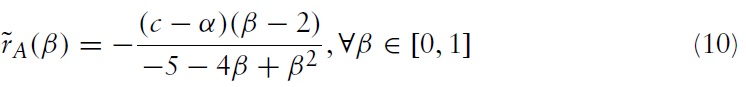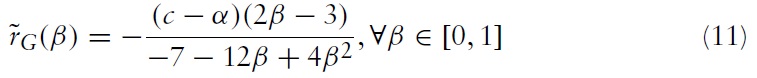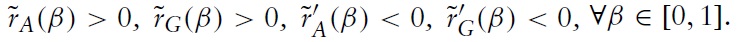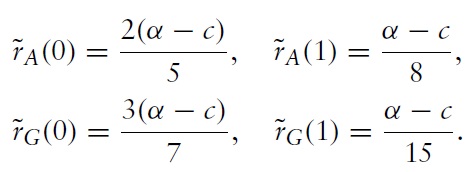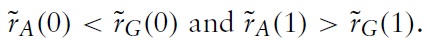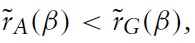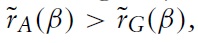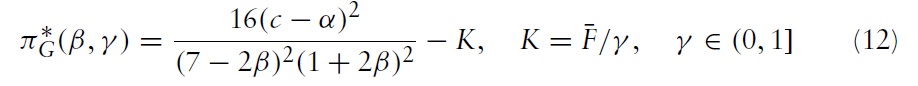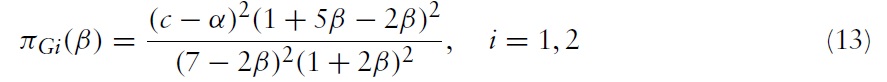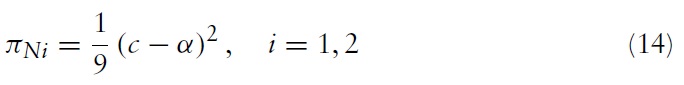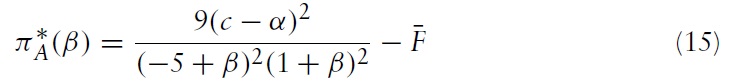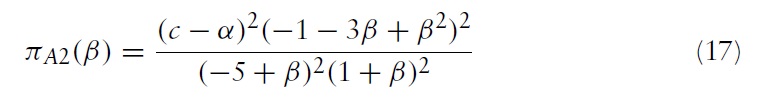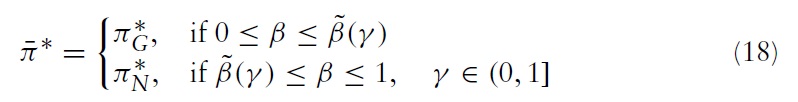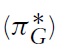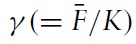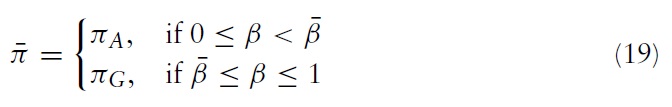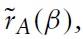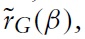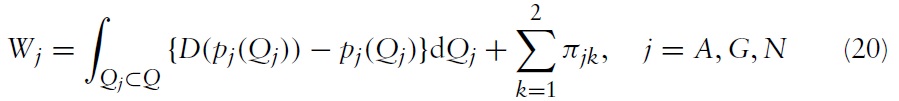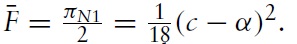Technology sourcing and technology transfer have become two important subjects, not only for academics, but also for firms of developed, aswell as developing, countries. Foreign direct investment (FDI) is one of the primary channels for transferring technology across borders. Developing countries have been trying to attract foreign firms with high research and development (R&D) intensity from developed countries as means of benefiting from technology sourcing and R&D transfer. In particular, the importance of overseas R&D spillovers for economic growth has been recognized since Coe and Helpman (1995) and Coe et al. (1997)). Much empirical work has provided evidence of the benefit from R&D or technology transfer across borders through total FDI.1

FDI can typically be broken into two components: greenfield investment, and cross-border mergers and acquisitions (M&A). Although there are many papers that examine the effects of total FDI on host firms’ productivity, the relationship between the various channels of technology transfer and the firm’s performance in host countries has received little attention. This sounds strange because not only greenfield FDI but also cross-border M&A have become the preferred mode of overseas investment by multinational companies, for both the bulk of foreign FDI in developed countries and for increasing shares in developing countries.

There have been relatively few empirical studies focusing on the relationship between the choice of entry mode and R&D spillovers.2 The paper by Liu and Zou (2008) is, as far as we are concerned, an exception. With Chinese hightech industry data, they examine differences in the impact of greenfield FDI and M&A on the innovation performance in a single framework and show that both greenfield FDI and M&A have a positive association with the R&D activities of foreign firms. They suggest that technology spillovers from FDI are generated through the R&D activities of foreign firms rather than through the competition effect of their production activities. Studying the difference in effects of entry modes on economic growth, instead of R&D, Wang and Wong (2009) show that greenfield FDI and M&A could have different growth impacts in host countries. They suggest that greenfield FDI positively affects economic growth, whileM&A affects economic growth only if the host country contains relatively large human capital. These two recent empirical works suggest that we should separate FDI into greenfield and M&A investments when we examine the channels of R&D spillovers and the impact of FDI on economic growth.3

Similar to the empirical literature, the theoretical literature has produced only a few papers up to the present: the interaction between technological innovation and firmentry mode choice has been a neglected issue. Buckley and Casson (1998) provide a general framework for an integrated analysis of the foreign market entry decisions, encompassing the choice between export, licensing, joint venturing, andwhole-owned foreign investment. They don’t, however, consider any spillover effects. Petit and Sanna-Randaccio (2000) develop a game-theoretical model to examine the impact of a firm’s mode of foreign entry on the incentive to innovate, as well as the effects of R&D activities and technological spillovers on the firm’s international strategy. Their results indicate that there is a positive relationship betweenmultinational expansion andR&Dinvestment, but they do not consider the firm’s choice between M&A and greenfield investment. Although there are many other papers of mode-choice between M&A and greenfield investments, such as Görg (2000), Hijzena et al. (2008), Nocke and Yeaple (2007), Kim (2009), and Raff et al. (2009), none of these studies focus on the possible interaction between a firm’s R&D activities and its choice of entry mode. Our model thereby aims to bring out this interaction and analyzes impacts of entry modes onwelfare.

In this paper, we build a model combining key aspects in the models of Petit and Sanna-Randaccio (2000) and others to construct one theoretical framework that allows for two entry modes with R&D spillovers.Within this framework, we can examine the interaction between a firm’s R&D decision and its foreign entry mode choice, including the choice between greenfield investment and M&A. A three-stage game-theoretical model is developed. In the first stage, a firm, which considers entering a foreign market, chooses its R&D level and makes an offer of M&A to one of the local firms in the host country. In the second stage, the local firm decides whether to accept or reject the offer. If the local firm rejects the M&A offer, then in the third stage, the foreign firm chooses one of the other two options, i.e., greenfield investment or staying out of the market.4 In the model we allow for imperfect appropriability (i.e., technological spillovers between firms). It is shown that if there exist relatively high R&D leakages and relatively small difference in cost between M&A and greenfield FDI, an R&D-intensive foreign firm tends to choose greenfield investment rather than M&A, while if there exist relatively low R&D leakages, the foreign firm is more likely to choose M&A rather than greenfield investment. The welfare implications of alternative entry modes to a host country are also discussed.

The rest of this paper proceeds as follows. Section 2 presents the model and examines the effects of R&D activities and technological spillovers on the foreign firm’s international expansion strategy. Section 3 investigates thewelfare effects of different entry modes of a foreign entrant firmon a host country. Brief concluding remarks are given in the final section.

1See Yokota and Tomohara (2010) and Keller and Yeaple (2009) for recent survey of empirical studies.  2There are some empirical studies on the impact of (only) M&A on performances of acquired firms. See Bertrand and Zunig (2006), Porrini (2004), and Ruckman (2005). See also Shimizu et al. (2004) and Cloodt et al. (2006) for a recent survey.  3In his brief note, Lall (2002) notices that firms with lower R&D intensity are more likely to buy technological capabilities abroad by acquisition, while those with strong technological advantages are likely to set up greenfield ventures.  4In Appendix A, we discuss a possible extension to include a third option for the entrant firm: the export option.

To analyze the effects of R&D investment with spillovers on the mode of foreign market entry, we set up a three-stage game-theoretical model. Suppose that there are three firms: one foreign firm and two local firms. The products of the firms are homogeneous.

In the first stage, the foreign firm chooses its level of R&D investment and at the same time makes an offer of M&A to one of the local firms. In the second stage, after observing the choice of R&D level of the foreign firm, if the local firm accepts the offer, then the foreign firm along with the acquired local firm competes against the other local firm in the local market and the game ends. If the M&A offer does not reach an agreement, then in the third stage the foreign firm chooses either to enter the market by greenfield investment or to stay out of the market.

It is assumed that the acquired local firm obtains the reservation profit, F, which is at least equal to or more than the profit it could get if it did not accept the offer. A strategy for the foreign firm prescribes a choice of the level of R&D, r, for the first stage where the strategy space is infinite and there is a choice of two possible actions at the second information set, i.e., (greenfield investment, stay out) where the strategy space is finite. If the foreign firm chooses greenfield investment, then the foreign firmcompetes against two local firms in the Cournot oligopoly fashion. If the foreign firm decides not to enter the market, then it gets zero profit and two local firms compete in the Cournot duopoly market.We assume hereafter for sake of simplicity that only local firm 1 has an option to accept or reject the offer of M&A by the foreign firm.

To simplify, we assume that only the foreign firm invests in R&D.We consider the process innovations, which can reduce the marginal cost of the investing firm. We also assume that two local firms enjoy the spillover effects from the foreign firm’s R&D investment by a certain proportion.The foreign firmchooses the level of R&D investment so as to maximize its profit in the first stage while the two local firms can benefit from the foreign firm’s R&D. It turns out that the foreign firmfaces a dilemma: the direct effect ofR&Dexpenditures can increase its profit and its indirect effect might reduce its profit by raising competitors’ productivities. This situation is pervasive in the realworld, especially for the case of foreign direct investment in developing host countries by firms from developed countries.

Define

as the profit functions of the foreign firm and two local firms, respectively, where j = A,G,N. Let A and G denote M&A and greenfield investment, respectively, and N represents the staying out strategy. An asterisk stands for the functions or variables for the foreign firm and subscripts 1 and 2 refer to the two local firms. Assume that all firms are forward-looking. Thus, a subgame perfect Nash equilibrium (SPNE) is adopted as a solution concept.

The foreign firm has a marginal cost, c_m, and the two local firms have the same marginal cost, c_d. If the foreign firm enters the local market with an M&A strategy, then it must pay the reservation profit, F, to the acquired local firm. Thus, the profit of the foreign firm is

and the profit of the acquired local firm (π_A1) equals F. The profit of the other local firm is π_A2 = max_q2 [(p − c_d)q2].

In the case of greenfield investment, the profit function of the foreign firm is

where K shows the fixed costs for greenfield investment including the purchase price of land, the building cost of the plant, the set-up cost of machinery, and so on.Without any loss of generality, we assume that K is greater than F, and further assume that F = γK, where γ ∈ (0, 1]. This means that the greenfield strategy is more costly than M&A. The profit function of the two identical local firms is now

Let r denote a level of R&D investment. Marginal cost of the foreign firm c_m is a decreasing function of r, c_m(r), where

We assume that the local firm’s cost structure is also affected by the level of foreign firm’s R&D investment, c_di(r), i = 1, 2. An increase in R&D investment of the foreign firm reduces the cost of the local firm.

Consider a linear market demand function. Suppose that the inverse demand function is p = α − Q, where Q is the sum of all three firms’ outputs, q^∗, q₁ and q₂, and α is a constant that is large enough so that the equilibrium price is strictly positive. We also assume that the cost functions can be written as follows;

where c is a constant.5 We assume that the total cost of R&D investment is a quadratic function of r, which implies that R&D activity is characterized with decreasing returns to scale. Since 0 ≤ β ≤ 1, thuswe have c_m ≤ c_d. Marginal cost of the local firm is

If β is zero, then no spillover effects exist, while β is unity, there emerge perfect spillover effects. With this setting, we can analyze the relationship between the entry mode choice of the foreign firm and the degree of spillover from the foreign firm to the local firm. The degree of β when the foreign firm chooses greenfield investment can differ from the degree of β when the foreign firm chooses M&A.

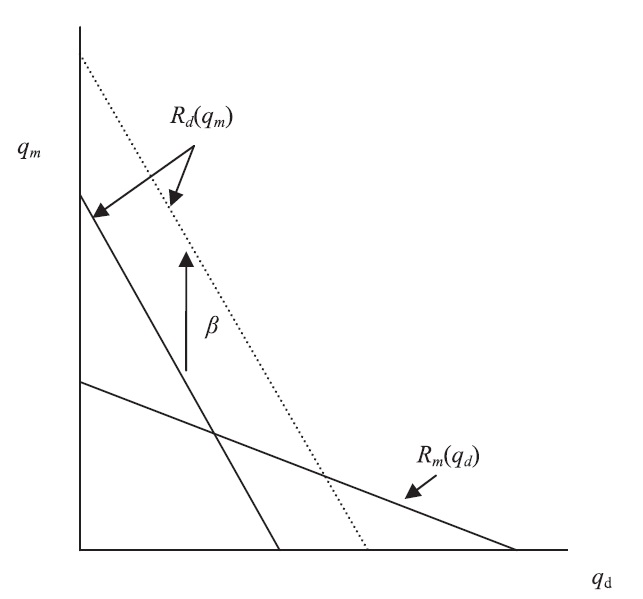
This model is solved through backward induction. In the third stage the foreign firmchooses greenfield investment or to stay out of the market. In this stage, equilibrium profits for the three firms can be derived from the first-order conditions.6 Since the best-response functions are downward sloping in these cases, players’ strategies are strategic substitutes. The case in which the foreign firm decides to enter the local market by a greenfield investment strategy can be shown in Figure 1.7 Figure 1 indicates that an increase in β induces an outward shift of the best-response function of the local firms. As a result, the equilibrium output of the local firms expands while the foreign firm’s output shrinks.

Solving the best-response functions, we have equilibrium profits as follows:

If the foreign firm chooses to stay out of the market, then equilibrium profits are:

In the second stage, local firms can choose to either accept or reject the offer of M&A. If local firm 1 accepts the offer, then equilibrium profits for the foreign and local firms are:

Here, F is a reservation profit,

In the first stage the foreign firm chooses its optimal level of R&D investment, which involves the following cost: Г(r) = r². Substituting equations (1) and (2) into profit functions and solving the profit maximization problem with respect to r, we obtain the optimal R&D levels under M&A and greenfield investment strategies, respectively:8

Proposition 1 In the cases of MඪA and greenfield investment, the optimal RඪD levels are positive and monotonically decreasing functions for any level of technology spillover; that is,

Proof. For the proof, see Appendix B. █

The above proposition indicates that the higher is the spillover effect, the lower will be the optimal R&D expenditures. This is due to the fact that a higher spillover effect implies a more serious free-rider problem so that the return on the firm’s R&D investment is lower.

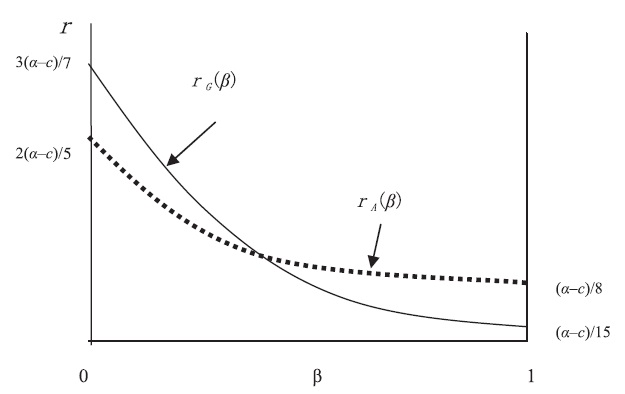
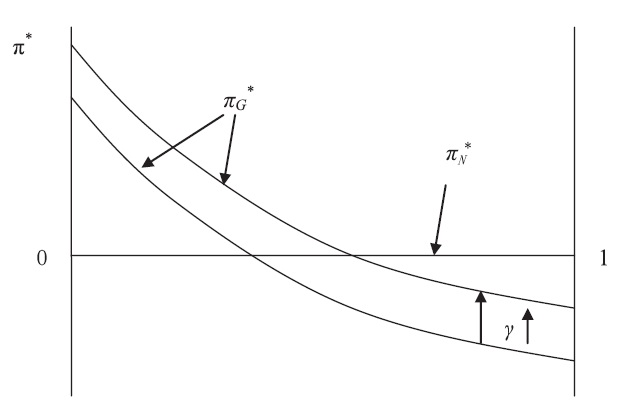
We next illustrate the difference in R&D expenditures between greenfield investment and M&A. This is done if we take the corner values of each optimal R&D expenditure when β = 0 and β = 1. From equations (1) and (2), it is straightforward to obtain the following results:

Clearly, we have

Graphically, we have the following relationship of the equilibrium R&D expenditures between M&A and greenfield investment.

These results are summarized in the following proposition,

Proposition 2 If the spillover effect, β, is small, then

that is,R&D investment is greater in greenfield investment than in MඪA. If the spillover effect, β, is large, then

that is, RඪD investment is greater in MඪA than in greenfield investment.

Proof. For the proof, see Appendix C. █

This proposition provides new insights into the relationship between R&D activity and the entry mode chosen by the multinational firm. It indicates that the post-entry R&D levels under different modes are crucially dependent on the extent of technological spillovers. Its economic intuition is clear. As shown in Figure 2, the absolute value of the slope of r_G(β) is larger than that of r_A(β;), which implies that the free-rider problem is more serious in the case of greenfield investment than M&A. Thus, the firm has less incentive to invest in R&D in the former case. This is simply because there exist two competitors in greenfield investment and one competitor inM&Aagainst the entrant firmin the post-entry market. However, Figure 2 indicates that when technological spillovers are low, the firm (when choosing greenfield investment) is willing to invest more in R&D than when choosing M&A. This is because cost advantages originating from R&D investment yield a higher payoff when facing two competitors instead of one competitor.

Combining these results with the profit functions, we have the equilibrium profits for each case. First, the equilibrium profits for the greenfield investment strategy are:

Here, γ represents the ratio of F¯ to K. In other words, if γ is larger, then the fixed costs of greenfield investment is smaller relative to those of M&A.

Secondly, if the foreign firm chooses to stay out of the market, then the equilibrium profits for the local firms are:

Finally, if the foreign firm chooses M&A, the equilibrium profits for the local firms are:

Although it is tedious, it is not difficult to showthat the foreign firm’s equilibrium profit is a decreasing function of β and that local firms’ equilibrium profits are increasing functions of β. This is intuitively plausible, because the foreign firm suffers from more profit loss from technology leakage to local firms with a larger β. On the other hand, local firms gain more from the technology spillover when β is larger.

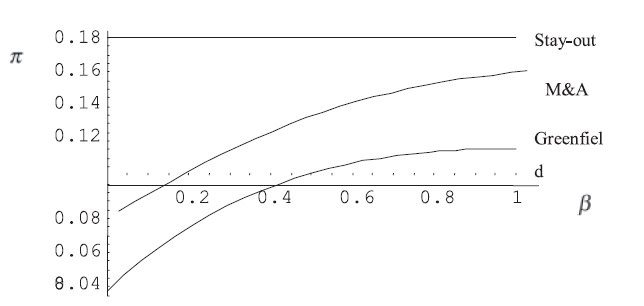
We next examine the relation between the level of R&D expenditures and the entry mode chosen by the foreign firm. As we discussed earlier, in the third stage of the game the foreign firm has two choices – that is, greenfield investment and staying out. In the third stage the foreign firm compares the profits of the greenfield

and staying-out options

First, we demonstrate the relationship between the profit of the greenfield

option and the profit of the staying-out

strategy, as shown in Figure 3.

Or,

If γ increases, then the profit curve of the greenfield

choice moves upward. Intuitively, since F is a fixed reservation cost, an increase in

indicates a decrease in greenfield investment fixed cost (K). A decrease in greenfield investment fixed cost improves the profitability of the foreign firm.

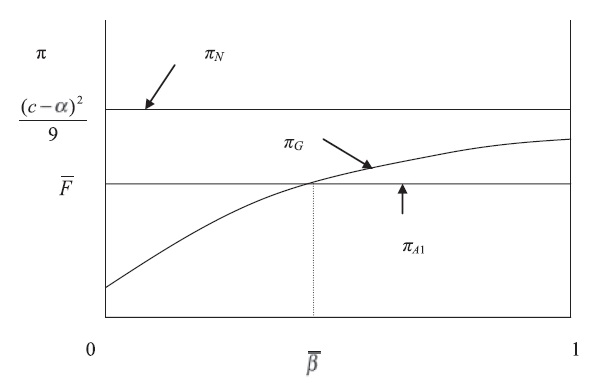
In the second stage of the game, local firms compare the possible profits from two alternatives: accepting the offer of M&A versus rejecting the offer and then competing with the entering firm via greenfield investment, or accepting the offer of M&A versus rejecting the offer and then competing with the other local firm. This is illustrated in Figure 4.

Figure 4 shows that the best circumstance for the first local firm is that in which the potential entrant chooses to stay out of the market.When the potential entrant chooses to enter the market, the choice of the local firmbetween accepting and rejecting the M&A offer depends on the degree of spillovers. If spillovers are small, then the local firm is likely to accept the offer and obtains the reservation profit,whereas if spillovers are large, then the local firmis likely to reject the offer, i.e.:

This is due to the fact that an increase in spillovers will increase the profits of the local firms when rejecting theM&Aoffer. As a result, the firm’s reservation price for the M&A offer is higher.

The following proposition summarizes one of our main results.

Proposition 3 In the linear model, there are three SPNEs depending on the degree of β and γ .

1. {the foreign firmchooses

the first local firmaccepts the offer, the second local firm enters the market},

2. {the foreign firm chooses

the first local firm rejects the offer, the foreign firm chooses greenfield investment, the second local firm enters the market}, and

3. {the foreign firm makes an offer, the first local firm rejects the offer, the foreign firm chooses staying-out, the second local firm enters the market}.

Proof. For the proof see Appendix D. █

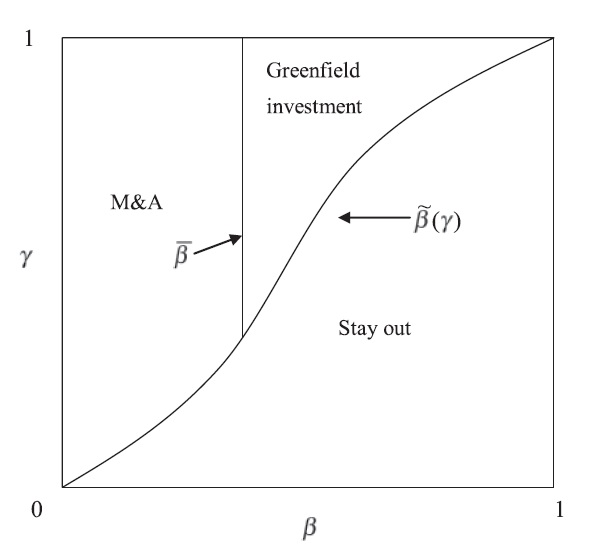
This proposition can be drawn graphically as shown in Figure 5.

Figure 5 illustrates the relationship between the SPNE and two important exogenous variables, γ and β. It clearly reveals that with larger spillover effects (or the free-rider problem is more serious), the foreign firmtends to choose to stay out of the market, unless the entry cost is lower.9 If the firm chooses to enter the market, then its choice between M&A and greenfield investment depends on the level of technology spillovers and the difference in entry costs between greenfield investment and M&A. If both the spillovers and cost difference are large, then in equilibrium the foreign firm is likely to choose greenfield investment. This is sensible since the local firm is more likely to reject the M&A offer under the case of higher spillover effects, and a larger γ implies a lower entry cost via greenfield investment relative to M&A. On the other hand, if both the spillovers and γ are small, then in equilibrium the foreign firm is likely to choose an M&A strategy to enter the market in the host country.

5We analyze only positive spillover effects. Possible negative spillovers, such as pollution and computer viruses, are not considered in this study.  6The second-order conditions hold for the foreign and local firms with any strategies, such as greenfield, staying out, and M&A.  7Rd(qm) indicates the aggregate of two local firms’ response functions.  8Under the ‘stay out’ strategy, foreign firm spends zero R&D efforts and the local firms do not receive any spillover effects.

The host country’s welfare, W_j, is defined as the sum of its consumer surplus (CS) and the total profits of the local firms:10

Since an increase in β indicates an improvement in the profitability of the local firms, total profits of the local firms (second term) increase in β. Since players’ output strategies are strategic substitutes as indicated in Figure 1, an increase in β induces an output expansion of the local firm(s) and an output contraction of the foreign firm. Since the direction of output changes in the foreign firm and the local firms are different, a change in equilibrium price is ambiguous a priori. Figure 6 provides numerical examples of consumer surplus in M&A, greenfield investment, and staying-out strategies for β ∈ [0, 1] when α = 1, c = 1/10, γ = 2/3, and

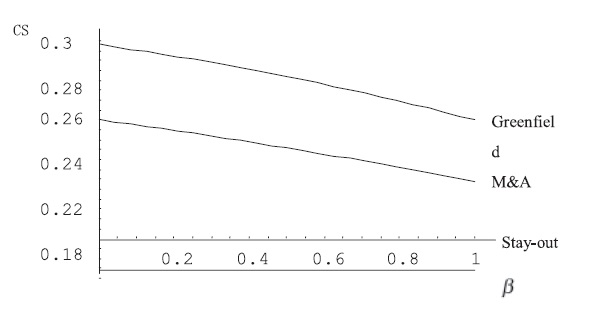
The consumer surplus in the case of greenfield investment is greater than that in theM&Aand staying-out strategies for any value of β. Figure 7 shows the total profits of the local firm(s). The total profits in the M&A case exceed those under greenfield investment for any value of β. With a relatively high β, the profits of the local firms in M&A are larger than the case in which the potential entrant chooses to stay out.

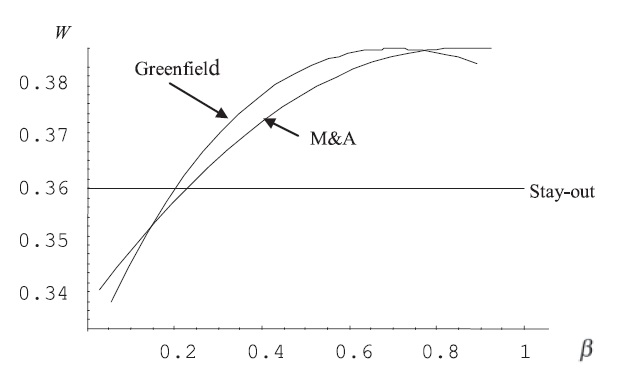
We next sum up the consumer surpluses and total profits to calculate the host country’s welfare for each strategy. Figure 8 shows that for a very low β, the total welfare of staying out is the best and greenfield investment is the worst. The total welfare of M&A becomes greater as β increases. However, in some areas of β, the welfare of greenfield investment exceeds the welfare of M&A and in the very high β area, the welfare of M&A is the best among the three options.

The economic intuition of the above results is as follows. The entry of a foreign firm probably reduces consumers’ prices as well as the total profits of the local firms. The change in the social welfare of the host country depends on the difference between an increase in consumer surplus and a decrease in producer surplus. When β is very low, the reduction in the profits of the local firms might dominate the increase in consumer surplus in either the case of greenfield investment or M&A, since the costs of the local firms might not be reduced very much. In addition, under this situation the reduction in the profits of the local firms might be lower in M&A than in greenfield investment, because the R&D level of the entrant firm is smaller in M&A, as shown in Proposition 2, so that the entrant firm’s cost advantage originating from R&D spending is relatively lower. As a result, the social welfare of the host country under greenfield investment is lowest.

When β is relatively high, the post-entry increase in consumer surplus might dominate the reduction in the total profits of local firms. Therefore, the social welfare of the host country in both greenfield investment and M&A is higher than the case in which the potential entrant chooses to stay out of the market. In addition, when β is not very high, the entrant firm spends more in R&D when it chooses greenfield investment rather than M&A, as shown in Proposition 2. As a result, the social welfare is higher in greenfield investment than in M&A. On the other hand, when β is very high, the entrant firm spends less on R&D when it chooses greenfield investment rather than M&A, because of a more serious freerider or technology leakage problem, as we discussed above. As the post-entry increase in consumer surplus still dominates the reduction in the total profits of the local firms, the social welfare will be higher in M&A than under greenfield investment under this situation.

To sum up, it is demonstrated in the paper that foreign direct investment via greenfield investment is not necessarily better than M&A from the perspective of a host country’s social welfare. It depends crucially on the extent of the spillover effects. This result has an important implication for antitrust policy.

9There is an infeasible areawhere γ equals zero since the range of γ is strictly positive by assumption.  10We assume that the foreign firm remits all profits back to its home country.

This paper examined amultinational firm’s choice between the different modes of FDI in cooperation withR&Dspillovers fromthemultinational to a local firm.We then developed a three-stage game-theoretical model to examine the relationship between a firm’s level of R&D with spillovers and its choice of foreign market entry modes.

We found that the choice of entry mode of the multinational firm crucially depends on the magnitude of R&D spillovers as well as the cost differences in entry modes. Our model predicts that, with relatively high R&D spillovers and relatively small difference in cost between M&A and greenfield FDI, an R&D-intensive firm tends to choose greenfield investment rather than M&A. On the other hand, with relatively small R&D spillovers, a multinational firm is more likely to prefer M&A to greenfield investment. It was also shown that the level of social welfare in the host country depends on the magnitude of technology spillovers. With moderate R&D spillovers, social welfare with greenfield investment is better than that of M&A together with higher consumer surplus, while the total profits of the firms are higher in M&A than in greenfield investment.

These findings lead to an important implication, particularly for antitrust policy of developing countries. To promote their economic growth, developing countries have been trying to absorb FDI from developed countries. While, in the situation with high R&D spillovers, foreign firms with strong technological advantages are likely to set up greenfield investment ventures to avoid the leakage of their technology, the social welfare of the host country may decline compared with M&A. This tradeoff will become more important in the world in which cross-borderM&Ahas become the common mode of FDI bymultinational enterprises.