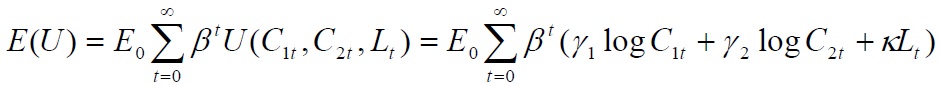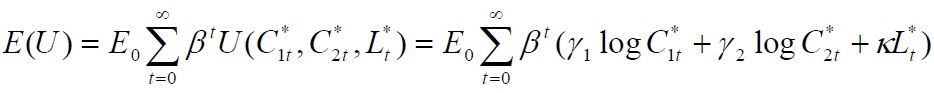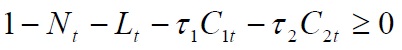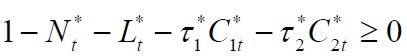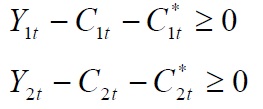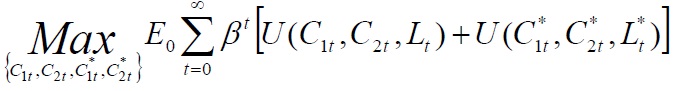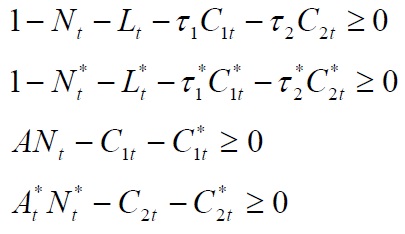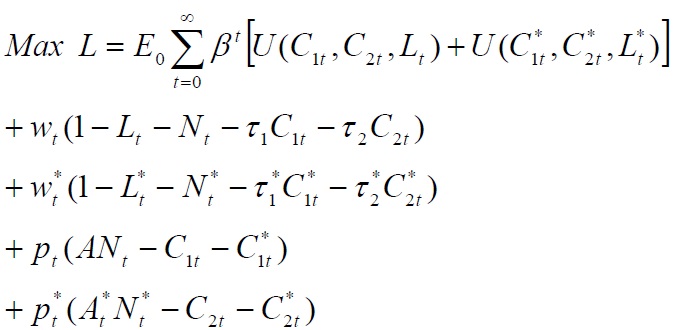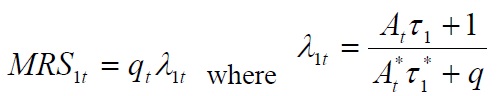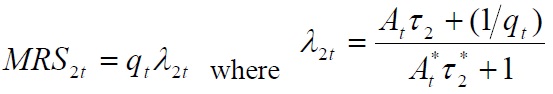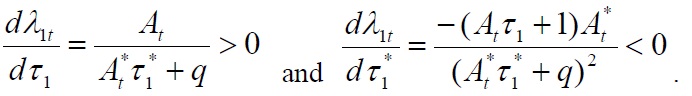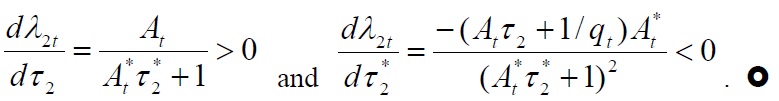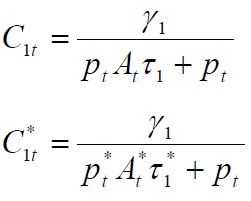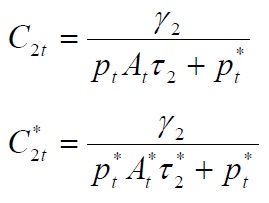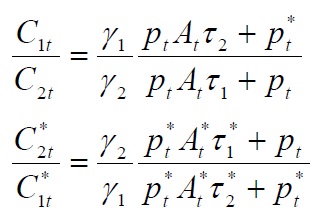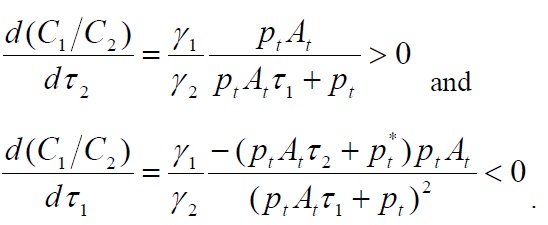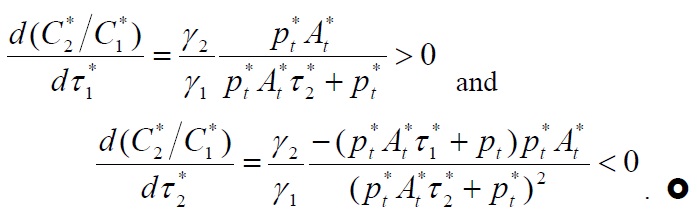Obstfeld and Rogoff (2000) advance the hypothesis that trade costs in good markets in an otherwise neoclassical and competitive environment can resolve six major puzzles in international macroeconomics, with two exceptions: the purchasing power parity and the exchange rate disconnect puzzles.1 They claim that accounting for these two puzzles requires additional friction: elements of monopoly and sticky nominal prices for goods and labor. However, while useful in addressing international monetary policy questions, recent sticky price models still lack the ability to explain the puzzling behavior of relative price across countries.

In this paper, we offer an alternative explanation to explain deviations from the law of one price in a framework of flexible prices. In particular, we focus on the role of transport cost, which is defined as the cost of moving goods from their production location to the consumption location in generating a natural wedge between prices in different locations. Our analysis embodies the notion that traded goods fluctuate in price, but their relative prices are bounded above and below international transaction costs. We explicitly rule out any role of monopoly power or price stickiness to focus on the channels we wish to emphasize. We then show that introducing transport cost in an otherwise standard competitive model improves its ability to explain deviations from the law of one price. This finding supports the view that relative price movements are bounded by fixed arbitrage limits, which are usually treated as proportional transport costs.

This paper also studies the extent to which transport cost can account for imperfect international risk sharing and home bias in trade. We find that imperfect risk sharing and the home bias problem naturally arise in the presence of real frictions such as transport cost. Our finding indicates that the international consumption correlation puzzle is virtually a corollary of the home bias puzzle.

The remainder of the paper is organized as follows. Section 2 reviews additional relevant literature. In Section 3, we describe the economic environment and develop a baseline model. Section 4 discusses the model’s key implications for relative price and international risk sharing. Section 5 offers concluding remarks.

1The six major puzzles include the purchasing power parity puzzle, exchange rate disconnect puzzle, home bias in trade puzzle, home bias in equity puzzle, Feldstein-Horioka puzzle, and international consumption correlation puzzle.

The law of one price (LOP) states that international relative price differentials should be arbitraged away so that identical goods in different locations should sell for the same price when expressed in a common currency. Purchasing power parity (PPP) is the notion that this should hold on average across goods in that similar baskets of goods should cost the same once expressed in a common currency. Knowing the extent to which data support these propositions is important for understanding nominal exchange rate behavior, the pricing of international financial assets and a host of other questions in international economics. Yet, the evidence from the empirical literature shows that not only are relative prices quite different across countries, but also such deviations are highly volatile and persistent. These characteristics of the real exchange rate remain the central puzzle in international macroeconomics literature, with the source of such puzzling behavior remaining unclear.2

Several avenues are explored to motivate the deviations of traded goods from the law of one price. Pricing to market combined with nominal rigidities is widely used to create volatile deviations in the real exchange rate (See, for example, Betts and Devereux (2000), Bergin and Feenstra (2001), Chari et al. (2002)). Such sticky price models build microfoundations of the price adjustment process by considering the role of imperfect competition in sustaining price differentials across countries. This approach argues that deviations from the law of one price are generated by the pricing-to-market behaviors of monopolistic providers, while nominal price rigidities maintain such deviations.

Recently, arbitrage cost models emerged as an alternative to explain deviations from the law of one price (See Sercu et al. (1995), Burstein et al. (2003), Crucini et al. (2005), Lee (2008)). The genesis of such models is derived from the recognition that sticky price models, while useful to address international monetary policy questions, still lack the ability to explain the persistence and volatility of the real exchange rate. In particular, when combined with the nontradability of goods, introducing arbitrage cost to an otherwise standard competitive model appears to dramatically improve its ability to rationalize the observed puzzling behaviors of the real exchange rate (Lee and Shin (2010). This paper fits into the second strand of literature.

In a world of complete financial markets, country-specific output risks should be pooled and thus, domestic consumption growth should not heavily depend on country-specific output risks. However, an expanding body of literature documents that international consumption correlations are not higher than expected. For example, Backus et al. (1992), Backus and Smith (1993), and Lewis (1999) point out that output growth rates are more correlated than consumption growth rates across countries. Crucini (1999), comparing the provinces of Canada, the states of the United States, and the G-7 countries, finds similar degrees of risk sharing within regions of Canada and the U.S. that exceed the risk sharing that occurs across the countries. In their seminal work, Obstfeld and Rogoff (2000) argue that risk sharing is more impaired internationally than domestically due to the costs to arbitrage trade. More recently, Sorensen et al. (2007) document that international home biases in debt and equity holdings declined during the period 1993–2003, while at the same time, international risk sharing increased. In particular, the authors demonstrate that less home bias is associated with more international risk sharing and that more financial integration is associated with more risk sharing. This paper analyzes the effects of transport costs on international risk sharing to show how the international consumption correlation and home bias puzzles can naturally arise in the presence of real frictions, even under the assumption of complete financial markets.

2Knowing that prices deviate persistently and by large percentages is not necessarily informative about the underlying economic reasons for the deviations. This is particularly true when the persistence and conditional volatility features of relative prices display similar patterns across different types of goods and services

In this section, we present a model of two countries and two goods. The home and foreign country, each specializing in the production of a single good using only labor as an input, are similar in two respects. First, they are assumed to be populated by a large and equal number of infinitely lived consumers with identical utility functions.3 Second, their financial markets are perfectly integrated, complete and frictionless. Transport cost is the factor that distinguishes one economy from the other. Individuals must transport their goods from the location of production to their location of consumption. Costs are measured in units of time, which are the fractions of an hour needed for individuals to transport goods from the location of production to the consumption location. Use of time in this process is what allows for alternative interpretations of the differences between the price in a centralized market and the economic value at the point of consumption. Therefore, in our model, transport cost is considered the time needed to transform the good in a way that is specific to the good, the location, or the individual.

Consumers in each country choose consumption of the home-produced tradable good ( C_1t ), foreign-produced tradable good ( C_2t ), and leisure ( L_t ) to maximize the expected value of lifetime utility:

in the case of the home country, and

in the case of the foreign country.4

A single representative agent allocates market time across the hours worked in the marketplace, hours of leisure and hours of transportation subject to the constraint that these three activities exhaust total hours available:

where N_t is the labor supply, and τ₁ and τ₂ are the transport costs associated with home and foreign goods faced by home individuals. The underlying idea is that individuals are required to spend time to transport goods in proportion to their consumptions.5

The foreign country faces an analogous constraint:

where N^*_t is the labor supply, and τ^*₁ and τ^*₂ are the transport costs associated with home and foreign goods faced by foreign individuals.

We assume that the financial markets of the two countries are complete and perfectly integrated, so that the goods’ market clearing conditions are given by

where Y_1t and Y_2t are the outputs of the home-produced tradable good and the foreign-produced tradable good respectively. Output is produced using labor and is affected by the productivity variables: Y_1t = A_tN_t and Y_2t = A^*_tN^*_t.

Finally, a social planner who allocates goods, production and transformation efforts to individuals solves the following problem:

subject to:

To solve the model, we specify the following Lagrangian problem and then solve the resulting system of first-order conditions:

where P_t, P^*_t, W_t, W^*_t are the multipliers on the constraints in the Lagrangian problem and have the following interpretations as shadow prices:

3We assume that two countries are of equal size, have identical preferences for home and foreign goods, and share a common currency to emphasize the channel through which transport costs affect the deviation from purchasing power parity and international risk sharing.  4We follow Rogerson (1988) who considers an environment in which non-convexities in the labor-leisure choice at the individual level lead to representative agent preferences that are linear in leisure.  5Transport cost in this model is similar to Lucas’ iceberg type transaction costs in that a proportion of the physical time is lost in transit.

The relative price of any pair of goods can be considered to be the marginal rate of substitution in the optimum.6 From the first order condition, the relative price of the home-produced good between the home and the foreign agents is then given by:

The relative price of the foreign-produced good between the home and the foreign agents is given by:

The terms λ₁ and λ₂ capture the impact of the cost of moving goods from the production location to the consumption location on the relative price faced at the final consumption stage, while q is their relative price before these costs are taken into account. In these terms, there are two sources of possible asymmetries across countries. First, asymmetries may arise from transport costs that differ across countries. However, even if τ = τ^* for every good, the relative price of the final good remains asymmetrical because the marginal cost of transporting the good depends on the wages of the agent.

Proposition 1. Deviations from the law of one price increases as transport costs increase.

Proof. From Equation (12), totally differentiating the deviations from the law of one price, measured by λ₁ with respect to τ₁ and τ^*₁ yields:

from Equation (13) we obtain:

Proposition 1 implies that transport costs play a crucial role in shaping the relative price behaviors between different locations. It is evident from Equation (12) and (13) that the relative prices simply reduce to a unity in the absence of transport costs, that is, MRS_1t = 1 in the case of τ₁ = τ^*₁ = 0 and MRS_2t = 1 in the case of τ₂ = τ^*₂ = 0 . However, the presence of transport cost drives a natural wedge between relative prices in different locations, leading to deviations from the law of one price for traded goods. This occurs because higher transport costs make goods less likely to be traded, and hence, limit the opportunity for arbitrage. For example, when the gains from trade are not high enough to offset transport costs, the implicit relative price is a matter of reading off the appropriate marginal valuations, expressed as the ratio of home and foreign marginal utilities evaluated at autarkic output points. The implied price differential is not sufficient at these output levels to justify paying the transport cost.

From the first order condition, equilibrium consumption of the home-produced good is given by:

Similarly, equilibrium consumption of the foreign-produced good is given by:

The primary implication of risk sharing is that individual consumption responds to aggregate shocks, but not to idiosyncratic shocks. This is because, under the circumstance of a complete financial market, countries effectively insure each other to the maximum extent possible against country-specific output shocks by pooling portfolios. Thus, the literature on risk sharing and complete markets predicts a positive relationship between consumption across countries. In our model, this is reflected by the fact that when countries are specialized in production, the price mechanism provides complete insurance for domestic and foreign residents alike, so long as τ = τ^* = 0.

However, in the presence of transport cost (τ > 0,τ^* > 0), productivity shocks in common industries are transmitted negatively between countries, and thus, the price mechanism provides no automatic insurance in this case. This is because when arbitrage costs are sufficiently large relative to the output differentials between countries, the gains from trade are not high enough to offset the transport cost, which leads to a non-trade equilibrium. Note that when τ = τ^* = 0, the consumptions of each good are perfectly positively correlated across countries. Our model degenerates to an autarky economy when the cost of moving goods from the production location to the consumption location is sufficiently large, in which risk sharing is prohibited.

Our model also indicates that transport costs play an essential role in determining home bias in trade, even under the assumption of a complete financial market. From the equations above, the consumption ratios between home and foreign goods faced by each country are given by:

Proposition. The proportion of domestic goods consumed by domestic individuals increases with transport costs associated with foreign goods and decreases with transport costs associated with domestic goods.

Proof. Totally differentiating Equation (18) with respect to τ₂ and τ₁ yields:

Similarly, from Equation (19), we obtain:

Suppose that two countries have identical preferences for home and foreign goods and share a common currency. When transport costs do not exist, the consumption ratio simply equals unity and consumption expenditures are evenly divided between the home and foreign goods. However, as shown in Proposition 2, if consuming imports requires more time in searching for and transporting goods relative to domestic products, then consumers will prefer to purchase domestic products, resulting in a home bias. This finding, in turn, implies that incomplete risk sharing naturally arises in the presence of real frictions such as transport costs. As noted by Obstfeld and Rogoff (2000), the international consumption correlation puzzle is almost a corollary of the home bias puzzle. This paper supports the view that transport costs play a significant role in home bias in trade, which is associated with less international risk sharing.

6The relative price is given by the ratio of the marginal utility of consumption abroad to that at home. See Apte et al (1996) for more discussions on the equilibrium approach of real exchange rates.

In this paper, we develop a two-country model to investigate the roles of transport cost in generating price and quantity puzzles in international macroeconomics, or more specifically, the purchasing power parity puzzle and the international consumption correlation puzzle. Transport costs are measured in units of time, which is the fraction of an hour needed for an individual to transport the goods from the production location to that individual’s consumption location. We show that deviations from the law of one price can naturally arise in the presence of transport cost, even under the assumption of a flexible price market. This result suggests that it is possible to generate deviations from the law of one price and purchasing power parity within a flexible price framework if a relevant real factor, such as transport cost, is introduced. We also find that transport cost leads consumption correlations to be affected by idiosyncratic output shocks, resulting in an international consumption correlation puzzle. A high level of home trade bias is also positively related to less risk sharing, indicating that the international consumption correlation puzzle is virtually a corollary of the home bias puzzle. This suggests that any market integration that reduces transport costs between locations should operate in a way that lowers the degree of home bias, but promotes international risk sharing. Our model ignores the potential importance of investment goods and substitution between home and foreign intermediate inputs. Thus, our future work should concentrate on incorporating capital goods into the model.