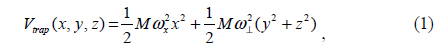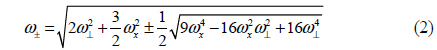Since the first realization of Bose-Einstein condensation in dilute gases confined in a magnetic trap [1, 2], intensive studies of the dynamical behavior of mesoscopic quantum systems have been performed [3-14], and it was expected to explain, for instance, the superfluidity of liquid helium [15]. The study of collective excitations (normal modes) is one of the standard methods used to characterize the behavior of highly-degenerate quantum systems. Since the first measurements of the lowest normal mode frequencies [3, 4] verified that the Gross-Pitaevskii equation (GPE) correctly predicted the dynamic behavior of condensate under excitation, the spectroscopy of the excited condensate has been extended to a variety of studies, e.g., frequency shifts [8, 16], mode coupling [8, 16, 17] and damping [6, 18].

In the hydrodynamic limit, which is applied to condensates with a large number of atoms, Stringari found the dispersion law for the elementary excitations of a dilute atomic Bose gas confined in both a harmonic trap and repulsive interacting forces [9]. For a cylindrically-symmetric potential,

where M is the atomic mass and ω_i is the angular frequency of oscillation along the i-axis, the m = 0 modes’ eigenfrequencies are given by [9]:

Here - and + signs are to represent monopole and quadrupole mode, respectively. This prediction has been successfully testified by experimental results [3, 4].

Since low-lying collective modes have an energy on the order of ħω_i for a harmonically confined Bose-Einstein Condensate (BEC), where ħ is the Planck constant divided by 2π , in previous studies collective excitation in a BEC was performed by applying a series of sinusoidal modulations near the resonance frequency on the confining potential [3-6, 8]. That is, the energy to excite condensate was provided from external sinusoidal perturbation.

From these previous results, we examined a possibility that a decrease of trap frequency also excites atoms with a contribution of the residual energy since modification of the trap geometry is the basic essential for the dynamical control of the ultracold atoms. The excitation behavior according to the adiabaticity of the deformation is also a topic of our question. For this, the atomchip is a good experimental apparatus because it can easily modify trap geometry at a micrometer scale within a wide range of changing times [19]. In this paper, we report on the observation of the dynamical behaviors of ultracold ⁸⁷Rb atoms on an atomchip under trap deformation. From the adiabatic deformation, we observed low-lying collective excitations and sound waves with pure condensate and a thermal cloud before the onset of a condensate, respectively. The frequencies were compared with theoretical predictions from the GPE in the hydrodynamic limit and to the sound wave. We were able to separate spatially the condensate into groups by different spin states by Majorana spin-flip through the non-adiabatic deformation. In addition, we investigated the population ratio of the different spin components by varying the final frequency in the rf evaporation step for the BEC.

The detailed apparatus and procedures we use for creating the BEC are described elsewhere [20]. In summary, our experimental setup consists of a compact double magnetooptical trap (MOT) apparatus with an anodically bonded atomchip which produces magnetically trapped ⁸⁷Rb Bose-Einstein condensates in the F = 2, m_F = 2 state. An atomic flux of high density is generated from a 2D⁺ MOT in the isolated 2D⁺ MOT chamber [21]. The atoms pass through a 750 μm hole and are trapped in a 3D-MOT. The atoms in the 3D-MOT are further cooled below the Doppler limit through a compressed-MOT and polarization gradient cooling. By using an external Z-wire trap, the atoms are transported from the initial 3D-MOT position to near the atomchip surface after optical pumping. About 9 × 10⁷ atoms can be trapped in an atomchip magnetic trap by the currents through the atomchip wires. After two-step rf forced evaporation, a BEC can be manipulated. Resonant absorption images were taken with the 100 μs illumination time, and the optical resolution was 3.5 μm.

The 26 × 26 mm² sized atomchip is formed by depositing 10 μm-thick copper conductor onto a 450 μm-thick silicon substrate (Fig. 1(a)). The central Z-shaped wire (called the Z-wire, 100 μm-width) is used with external bias fields to create an Ioffe-Pritchard trap. Higher trap frequency along the x-axis can be obtained with a dimple trap that is created by running a current through the wire that is perpendicular to the Z-wire (called dimple-wire, 100 μm-width). The two wires beside the Z-wire are designed for an rf-induced potential experiment and are not used for this study. To investigate the motion of the condensate under a trap deformation, the magnetic field of the dimple trap is modified by a ramp-down of the dimple current I_d. Since the dimple current makes an x-directional field at the center of the trap, the x-directional trap frequency can be changed dominantly with the current (Fig. 1(b)). Fig. 1(c) is the measured anisotropy (λ=ω_x /ω_⊥) of the deformed trap as a function of the final Id in the range of our performance. More reduction of the current makes the trap more anisotropic [22].

For this study, initially, a BEC was prepared after rf forced evaporative cooling within 2.3 s which is sufficient to damp the atoms’ motions induced by the atomic cloud transfer. The prepared BEC typically contains 5.5 × 10⁴ atoms without recognizable thermal fraction and is positioned at 180 μm below the atomchip surface with the Z-wire current I_z = 2.98 A, the x-axis bias field B_x = 6.86 G, the y-axis bias field B_y = 33.10 G and the I_d = 0.98 A.

Trap deformation for investigating dynamical behavior was performed in two ways, adiabatic and non-adiabatic changes, by changing the ramp-down duration of dimple current, which is determined by the speed changing trap potential.

For the adiabatic deformation, the dimple current I_d was ramped down from 980 mA to its final value within 10 ms, corresponding to a reduction of the trap frequency. The 10 ms ramping time was sufficient to guarantee adiabaticity for our experiments because the Larmor frequency at the center of the dimple trap can be estimated as > 2 MHz by the trap bottom (~ 700 kHz corresponding to ~ 1 G). After the deformation, the deformed trap was maintained for a variable time, ranging from 0 ms to 60 ms, to strobe the free dynamical behavior in the deformed trap. The atoms were observed along the y-direction by absorption imaging after a sudden switch off of the magnetic trap and 10 ms time-of-flight. There was no trap loss during the trap maintenance time over which the delay was varied.

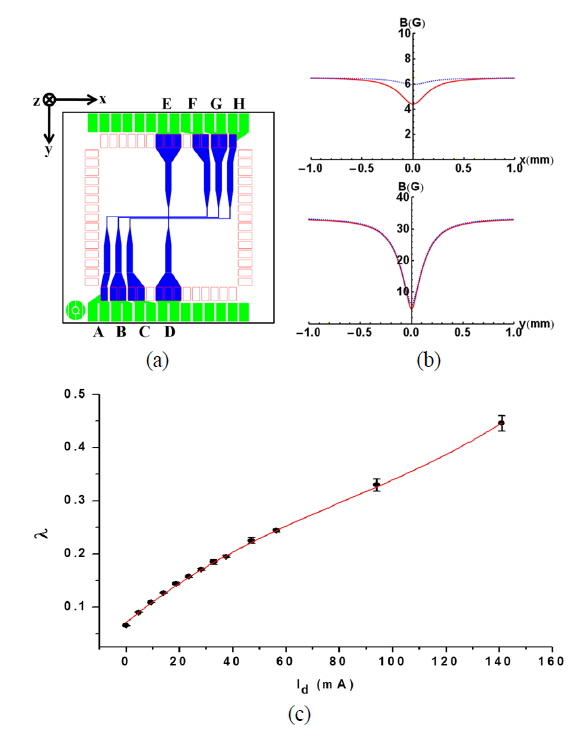
The condensate was excited by the deformation of the trap and two modes of collective excitation were identified from the absorption images: dipole and monopole m = 0 modes. The x and z-directional center-of-mass oscillations (dipole modes) were excited because change of the dimple current displaced the minimum point of the trap slightly due to asymmetry of the trapping Z-wire. From this center-of-mass oscillation, accurate values of trap frequencies can be obtained because dipole mode excitations are not affected by the interatomic forces, nor by the temperature or the statistics [23]. Figure 2(a) shows the shape oscillation of a condensate under the deformation with final I_d = 47 mA. The condensate exhibited sinusoidal width oscillation with large amplitude along the x-axis. In addition, the z-directional width oscillated with in-phase and relatively small amplitude (Fig. 2(b)). Such width-oscillation behaviors represent monopole m = 0 mode (breathing mode) [9, 10]. Note that the widths were convoluted since the condensate was observed after ballistic expansion. The striations parallel to the z-direction is the optical diffraction fringe formed by the narrowed condensate. The widths of the clouds were extracted from a Thomas-Fermi fit of the absorption profiles along the x and z-axis at the center. Beyond the optical diffraction limit, which is when the striations occurred, the widths were calibrated from the diffraction spacing. For comparison with the theoretical expectation, the x-directional oscillating widths were fitted with an exponentially decaying sine function, σ(t) = σ(0) + A exp(–t/τ)sin(2π(t–φ) /T), and the frequency of the breathing mode and the decay rate were determined as 127.9±1.4 Hz and 28.2±5.1 s^-1, respectively. The expectation value of the breathing mode followed by Eq. (2) was ω/2π = 126.4 Hz because the condensates were in the hydrodynamic limit Na/a_HO=150≫1 and the trap frequencies of the deformed trap were determined as ω_x/2π = 80.2 ± 1.8 Hz and ω_⊥/2π = 367.3 ± 0.5 Hz from the dipole mode oscillation. The experimentally determined frequency is consistent with the theoretically expected value within an error bound. The same deformation experiment on a thermal cloud at T/ T_c ≈ 1.5 was performed. Fig. 2(c) shows the width oscillation and the frequency was 152.5±7 Hz. This frequency is also consistent with 2(ω_x/2π) = 160.4 ± 3.5 Hz, which is expected for the non-interacting Bose gas [9]. These width oscillations in a thermal cloud can be understood by sound waves. In addition, rapid diffusion of the cloud is identified from the fit line in Fig. 2(c), which indicates the exponentially decaying sine function for accounting for diffusion due to heat, . We consider the fast diffusion of the cloud is due to the finite depth of the deformed trap and collision induced thermalization of the excitation. From those results, which were consistent with the theoretical expectation, we were able to conclude that the adiabatic deformation of the trap, not by sinusoidal modulation but by ramping, induces collective excitations on the BEC.

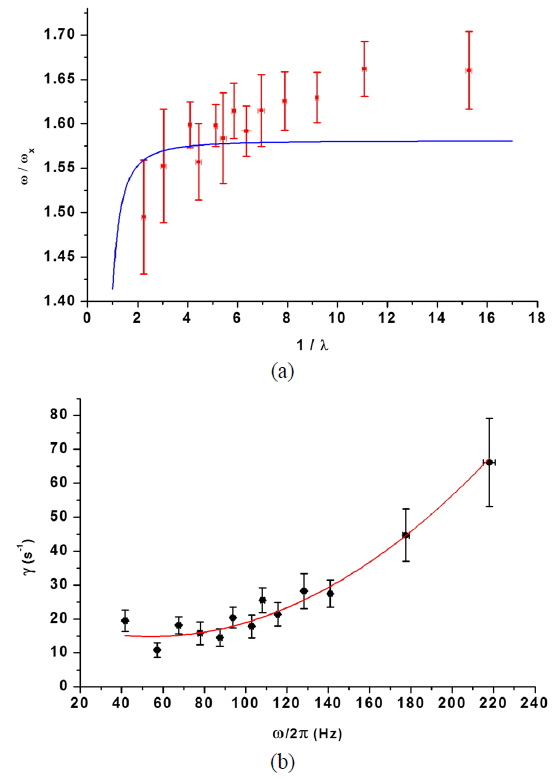
After the confirmation of the collective monopole m = 0 mode on the condensate, the experiment was done with final I_d range of 0 to 94 mA. We were not able to include the data with the final I_d over 94 mA because the amplitudes of the dipole mode excitations were too small to determine the trap frequencies. The frequencies of the monopole m = 0 mode for various deformed trap geometries were normalized by the corresponding x-directional trap frequency and plotted as a function of the trap anisotropy parameter 1/λ as shown in Fig. 3(a). The solid line is the theoretical prediction of the mode frequencies in the hydrodynamic limit as given in Eq. (2). Despite the discrepancy, the measured frequencies demonstrate a similar tendency to the anisotropy and are well below 2(ω_x/2π) which is expected for noninteracting gases. The mode frequencies higher than the prediction for the highly anisotropic trap can be understood as the effect of anharmonic shift due to the large response amplitudes [5]. Fig. 3(b) presents the decay rate γ as a function of the breathing mode frequency. Note that reduction of the final dimple current causes not only a decrease in the mode frequency but also an increase in the response amplitudes. However, we conclude that the decay rate is dominantly affected by the mode frequency because a damping rate of the m = 0 condensate mode tends to increase with the response amplitude [5]. The damping rate dependent on mode frequency can be understood with the fact that the atom-atom collision rate is proportional to the velocity of the atoms.

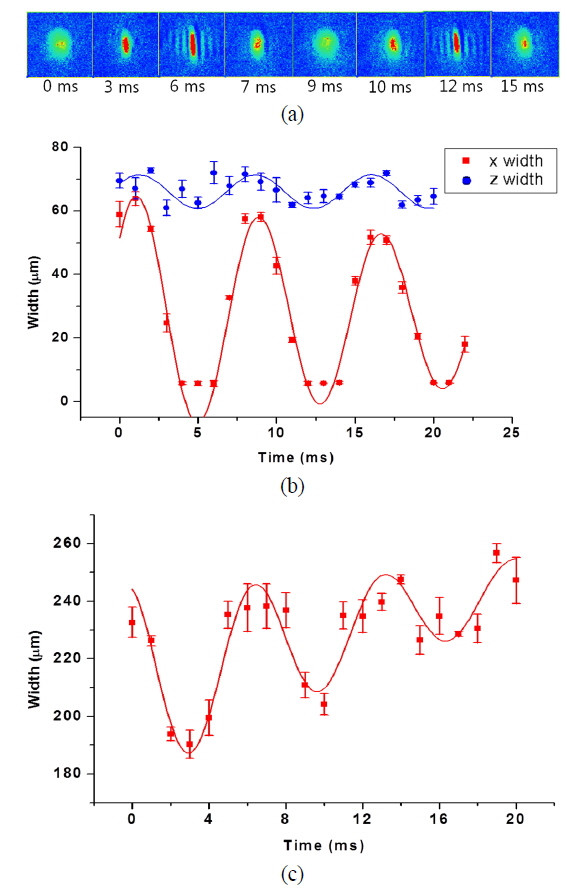
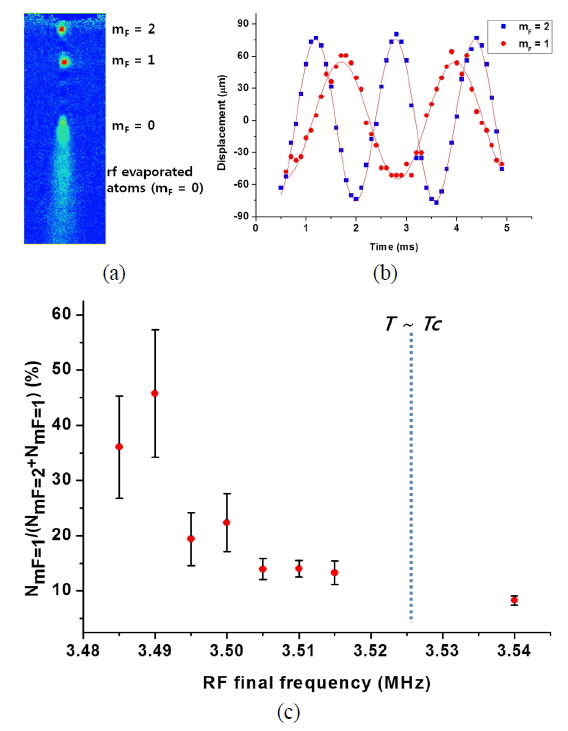
To investigate the dynamics under a nonadiabatic deformation, we ramped down the dimple current to 47 mA within 20 μs, ~50 T/s, which is sufficiently fast to induce Majorana spin-flips. A variable time delay was introduced between the deformation and the observation of the cloud. The absorption imaging was performed after a 2 ms time-of-flight. Figure 4(a) is the absorption image taken with a 2.8 ms time delay and shows the three spatially separated components of ultracold atoms with different spin states: m_F = 2, m_F = 1 and m_F = 0. During the deformation, the BEC prepared initially in the m_F = 2 state underwent a fast change in the magnetic field and was spin-flipped by Majorana transition [24, 25]. After the transition, the spin-flipped m_F = 0 component freely fell by gravity while the m_F = 2 and the m_F = 1 state components oscillated in the deformed trap with different spring constants (Fig. 4(b)). The oscillation frequencies of the two components have a ratio of which is highly consistent with the expectation . Note that there were no detectable m_F = -2 and m_F = -1 state atoms because they experienced outward forces from the deformed trap and rapidly dissipated. In addition, we investigated the population ratio of the m_F = 1 atoms to the sum of the m_F = 1 and the m_F = 2 atoms as a function of the final frequency used in the rf evaporation (Fig. 4(c)). Each data point represents 30 measurements. The ratio shows an obvious increasing tendency as the final frequency decreases. For now, we do not have a clear explanation for this. However, from the fact that the population of the m_F = 2 state sharply decreases with the frequency while the population of the m_F = 1 state remains nearly constant, an inhomogeneous trapping field can be the most plausible reason for the tendency. Some other possible reasons need to be studied, such as temperature dependency of the transition.

In summary, we studied the dynamical behaviors of ultracold atoms on an atomchip under a trap deformation. With an adiabatic deformation, a BEC shows collective excitations, m = 0 monopole and dipole mode oscillations in the deformed trap. The width-oscillation frequency difference between the pure condensate and the non-condensed atomic cloud was clear evidence for the fact that the trap deformation was able to induce collective excitation on the BEC. The measured breathing mode frequencies in the range of the measurements were consistent with the prediction of the mean-field theory in the hydrodynamic limit. Under a nonadiabatic trap deformation that induced a Majorana transition, ultracold atoms were able to be separated spatially due to their trap frequency difference in the deformed trap.

Although collective excitation is not a new topic, the collective behaviors of the BEC on an atomchip is an interesting subject, for example, nonlinear dynamics [26, 27], because the trap geometry can be changed with a high aspect ratio, wide range of time, and high anharmonicity, etc. We believe this data, along with further theoretical study, will help in dynamical control of ultracold atoms on an atomchip.