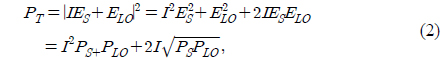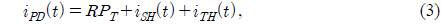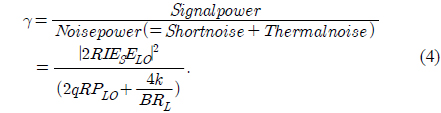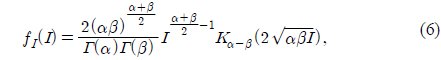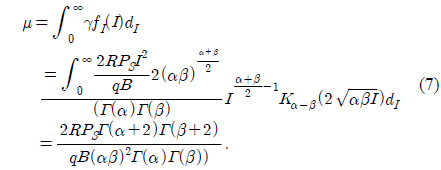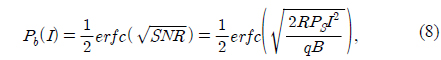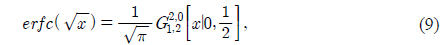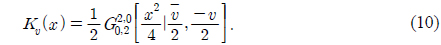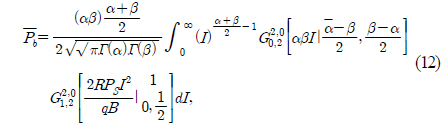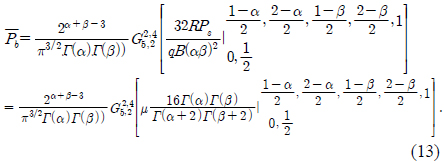Free-space optical (FSO) communication systems [1-5] are commonly used to provide an attractive and cost-effective link for high-data-rate wireless transmission. FSO systems support diverse applications ranging from highly directive point-to-point links for terrestrial last-mile and long-haul intersatellite solutions to quick and efficient deployment in densely populated urban areas or in unstructured environments such as disaster-prone areas.

FSO systems utilize a free-space medium for transmission, but they are inherently affected by atmospheric conditions, among which turbulence has the most significant effect, especially for high-data-rate point-to-point links. As such, it is an interesting problem to analyze the degradation of signal strength due to scintillation of the optical signal as well as link performance against atmospheric turbulence channels. In atmospheric turbulence channels, the coherence time of the channels is on the order of milliseconds, which is typically much larger than the one-bit time interval of gigabit-per-second (Gbps) FSO signals [6-11]. Hence, for a one-bit time interval, the FSO channels are modeled as a constant and random variable that is governed by a log-normal, K, or gamma-gamma distribution. The gamma-gamma distribution is a tractable mathematical model with a multiplication of two parameters of small-scale and large-scale irradiance fluctuations, the probability density functions (PDFs) of which are independent gamma distributions, and it provides excellent agreement between theoretical and simulation results [6-8].

Many authors have intensively researched and analyzed several implementation techniques for FSO systems under turbulence. In Ref. [8], a performance analysis for intensity modulation-direct detection (IM-DD) FSO systems over gamma-gamma turbulence channels was presented. For coherent FSO systems, Refs. [12] and [13] proposed alternative implementations enabling a higher receiver sensitivity than that of IM-DD, especially when the power of the local oscillator laser is sufficiently high; Refs. [6] and [14] presented analyses of coherent heterodyne DPSK systems over K and gamma-gamma turbulence channels, respectively, considering thermal noise caused by the high operating temperature of FSO systems. Coherent PSK requires the proper control of laser coherence, which is challenging in FSO systems because of difficulties associated with the phase-locking of the local oscillators. However, coherent PSK is expected to provide performance benefits over DPSK. Furthermore, there are known results indicating that the performance of coherent FSO systems is limited by the shot noise of the receiver, which heterodynes with a local oscillator laser having sufficiently high power; this needs to be analyzed further under turbulence channels.

In this study, we derived a generalized closed-form expression for the average BER performance of coherent FSO systems by using binary phase shift keying (BPSK) over atmospheric turbulence channels, in which the turbulence-induced fading of the signal intensity is described by a gamma-gamma distribution. Moreover, theoretical results are provided to understand the degradation of performance as a function of scintillation depth. Analytical results are further confirmed through Monte Carlo simulations and VPI transmission Maker results.

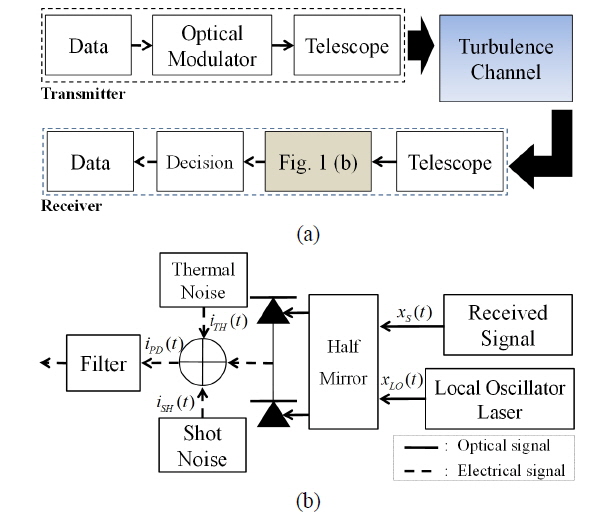
The overall architecture of coherent FSO systems is shown in Fig. 1 (a). The optical modulator processes data by using a laser at a transmitter. The output signal of the optical modulator is transmitted via atmospheric turbulence channels between telescopes. In Fig. 1 (b), the received signal is combined with a local oscillator laser through a half-mirror at a receiver. Then, a photodetector detects the compound optical signals to generate the photocurrent. Finally, a decision module extracts data. In this section, we explain the coherent PSK receiver in detail because it is the basic model for coherent receivers and can be adapted to other modulation receivers. In Fig. 1 (b), the received optical signal and the local oscillator laser in scalar form can be expressed, respectively, as [12, 13]

where E_S is the electrical field of the received signal, I is the intensity-fading coefficient, a = ± 1 is the information, f_c is the optical carrier frequency, and E_LO is the electric field of the local oscillator laser. The total power of the received signal and local oscillator laser is

where P_S is the power of the received signal and P_LO is the power of the local oscillator laser. Additionally, the output current of the photodetector is expressed as

where R is the responsivity of the receiver; the short noise (i_SH(t)) and thermal noise (i_TH(t)) have power spectral densities (PSDs) of G_SH = RP_LOq and , respectively; q is the electron charge; k is the Boltzmann constant; B is the noise-equivalent bandwidth of the filter; and R_L is the load resistance. When i_PD(t) is low-pass filtered to limit the noise power, the instantaneous signal-to-noise ratio (SNR) is given as

In coherent FSO systems, if the power of the local oscillator laser were sufficiently high, the second term in the denominator of Eq. (4) would vanish. Thus, Eq. (4) is reduced to [5]

As in [7] and [8], the PDF of a gamma-gamma distribution is represented by the product of small-scale and large-scale irradiance fluctuations, both of which have gamma distributions. The gamma-gamma distribution is

where I >0, is the average irradiance of the channel, α and β are the scintillation parameters, K_s(ㆍ) is the modified Bessel function of the second kind of order ε , and Γ(ㆍ) is the Gamma function. Here, α and β are defined based on the atmospheric conditions, as in [8].

In this section, we derive the average BER of coherent FSO systems according to BPSK modulation. We first calculate the average SNR (µ) using [15, Eq. 07.34.21.0009.01] as follows:

The conditional BER, P_b(I), for coherent systems is represented as

where erfc is the complementary error function. To obtain a closed-form expression, we used the following Meijer G functions that were reported in [15, Eq. 07.34.03.0619.01 and Eq. 07.34.03.0605.01], which are, respectively, expressed as

and

Thus, the conditional BER (Eq. 8) and gamma-gamma distribution (Eq. 6) can be represented by the Meijier G function using Eqs. 9 and 10. Thus, the average BER ( ) can be obtained using the following integral:

By substituting Eqs. (6) and (8) into Eq. (11), we can obtain the following equation:

Finally, by using the classic Meijer integral of the two G functions [15, Eq. 07.34.21.0011.01], Eq. 12 is simplified as follows:

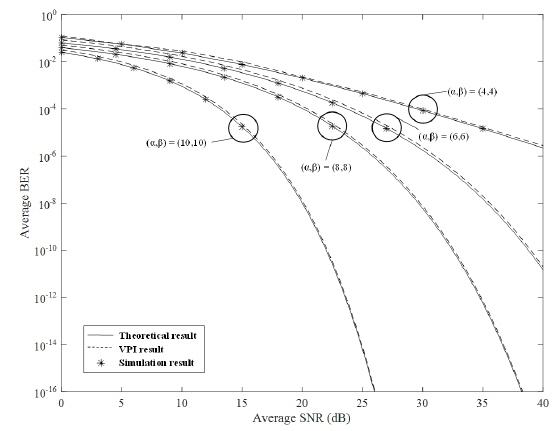
Figure 2 represents the results for a closed-form expression of the average BER, , as a function of the average SNR at different turbulence strengths. For instance, we considered the following turbulence strengths: (α :β )∈ {(4,4),(6,6),(8,8),(10,10)}. Monte Carlo simulation results are included as a reference to validate our theoretical analysis. For creating gamma-gamma turbulence channels in the simulation, we used the multiplication of two random variables with a gamma distribution [3]. Then, we confirm that the PDF from a gamma-gamma random variable using the histogram method in MATLAB is the same as Eq. (6). Owing to the long simulation time, only simulation results up to BER = 10⁻⁵ are included. The simulation results demonstrate an excellent agreement with the results of theoretical analysis. Considering that BER = 10⁻⁹ is a practical performance target for an FSO system, our analytical results can serve as a simple and reliable method to estimate BER performance without resorting to lengthy simulations. In addition, to clarify our analysis further, we confirm its accuracy through system-level simulations using VPI transmission Maker. Because the validity of the FSO toolboxes of VPI transmission Maker has been established by verified FSO experimental data, we consider the results from VPI transmission Maker as an alternative experimental approach. The outputs of VPI transmission Maker are completely consistent with that of our analysis, as well as that of our MATLAB simulation.

Figure 2 plots the average BER as a function of the average SNR for different turbulence channel strengths. Recall that the channel strength depends on the scintillation parameters, α and β, such that the turbulence effects become stronger as α and β decrease. We observe that the BER of the coherent FSO system under a strong turbulence effect of (α,β) = (4,4) is significantly higher than that under a weak turbulence effect of (α,β) = (10,10). More specifically, in the weak turbulence case, the average BER with an SNR of 20 dB is less than 10⁻⁸. In the strong turbulence case, the average BER severely increases to 10⁻³ at 20-dB SNR.

We obtained a closed-form expression for the average BER of coherent FSO systems over atmospheric turbulence channels with a gamma-gamma distribution by using special integrals and transformations of the Meijer G function. Furthermore, we simulated the average BER performance using the Monte Carlo method to confirm the theoretical results. Simulation results show an excellent agreement with the analytical results. Therefore, we can more easily predict BER performance by using a simple closed-form expression without any complicated calculation. In practical terms, when we establish coherent FSO systems, we can create an engineering table by using the derived BER.