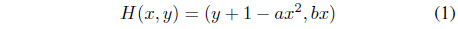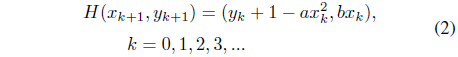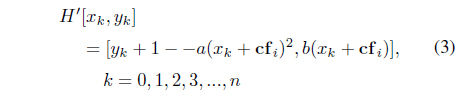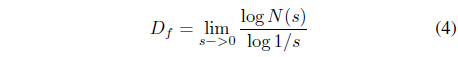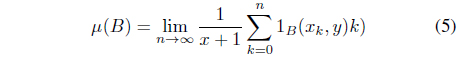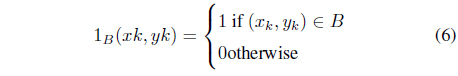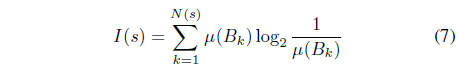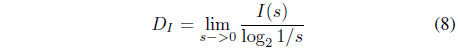Chaos theory is the study of the irregular, unpredictable behavior of deterministic and nonlinear dynamical systems. Using a chaos interpretation allows us to evaluate the characteristics existing in a system’s status space, using a time-series, to extract the chaos characteristic understanding, these characteristics enable us to conduct a high-precision interpretation [1-4].
Therefore, this paper proposes a new method that extracts character features and recognizes characters using the fractal dimension of chaos theory; it precisely recognizes minute differences with a strange attractor created from the Henon system. This paper presents a high-precision character recognition system.
The same kind of difficulties are found in recognizing Hangul (Korean) characters, as are found in English word recognition because Hangul characters have a similar hierarchy graphemes are combined to form characters [5-7]. In order to solve the variability and ambiguity problems, statistical and structural methods have been mainly used in previous studies.
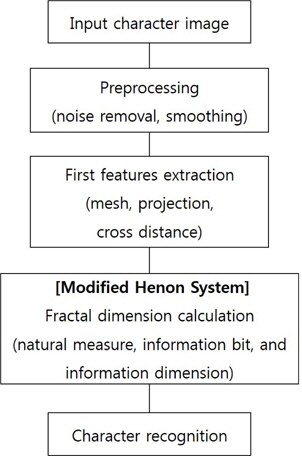
2. Proposed Character Recognition System
The proposed system first obtains the mesh, projection and cross-distance features from the character images. The features are converted into time-series data. Then, using the modified Henon system suggested in this paper, each character’s attractor for a standard Korean character set, KSC 5601, is reconstructed (Figure 1).
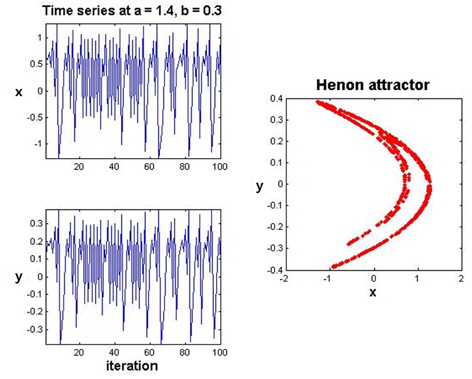
Henon’s Attractor is a discrete dynamical system in two dimensions. It was suggested by the French astronomer Michel Henon in 1976 as a simplified model for the dynamics of the Lorenz system [8]. Because of its simplicity, it lends itself to computer studies and numerous other investigations. Moreover, the gently swirling, boomerang-like shape of the attractor that arises through the dynamics is aesthetically very appealing. This object is now known as the Henon attractor (Figure 2).
In a manner which we will specify, the Henon system leads from the one-dimensional dynamics of the quadratic transformation to multi-dimensional strange attractors.
The stretch-and-fold action of the Henon system occurs in two dimensions, with coordinates denoted by
where
Similar to the logistic equation, these dynamics depend dramat ically on the choice of the constants
2.3 Creation of a Character Attractor
The system extracts the first feature from the input character images, and the feature is converted into time-series data. Then, using the modified Henon system suggested in this paper, the character attractors are reconstructed; i.e.,
where cf
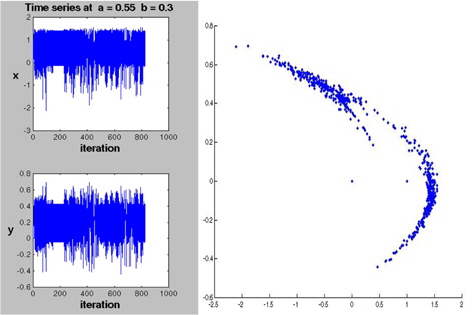
a = 0.55 and b = 0.3
The best character attracters are reconstructed in this case (Figure 3).
3. Analysis of a Fractal Dimension
The concept of a fractal dimension has inspired scientists to produce a host of interesting new work and fascinating speculations. Indeed, for a while, it seemed as if the fractal dimension would allow us to discover a new order in the world of complex phenomena and structures.
In this paper, in order to analyze the chaotic degree of each character’s attractor, the system obtains the last features of the character image after calculating the box-counting dimension, the natural measure, the information bit, information (fractal) dimension [8-10].
The box-counting dimension is related to the self-similarity dimension and is the most used measurement in all the sciences. The reason for its dominance lies in its easy and automatic computability by machine. It is straightforward to count boxes and to maintain statistics allowing dimensional calculation.
We place the structure on a regular mesh, with mesh, size
where, scaling factor
To compute the box-counting dimension, we first find a rectangular region that contains the complete attractor. To overcome this shortcoming of the fractal dimension, boxes should be weighted according to how many times an orbit visits them. Consider an open subset
We can count the number of times an orbit
Formally,
where 1
and is the number of points from the orbit
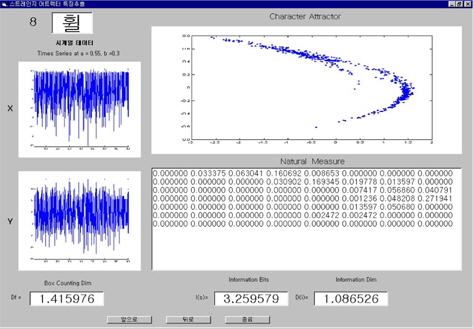
The natural measure can be understood as a means of quantifying the mass of a portion of the attractor. The calculated result of the natural measure is shown in Figure 4.
3.3 Information Bit and Dimension
The theoretical foundation was given by Claude Shannon in 1948. The logical approach would be to replace the simple box-count by a counting procedure in which each box is weighted according to its natural measure. Thus, places which the orbit passes through very frequently have a stronger impact on the calculation than boxes which the orbit rarely visits. In terms of a formula, we replace
Here, the sum ranges over all
4. Implementation and Experimental
First, using modified the Henon system suggested in this paper, each character’s attractor for the standard Korean character set, KSC 5601, is reconstructed. Next, in order to analyze the chaotic degree of each character’s attractor, the system finds the last features of the character image after calculating the box-counting dimension, natural measure, information bit, information (fractal) dimension.
Even though calculating of the box-counting dimension for a character attractor in character recognition is very simple, it only determines whether the attractor exists in a fixed box size.
Thus, is very sensitive to noise and does not well reflect the characteristic information of the character. Therefore, after using the information dimension and information bit computed based on the natural measure, which shows the characteristic information of character, we do global and detailed classifications by means of a statistical method using the minimum distance value of the characteristic vector.
In the experiment, we adopted Henon system parameters (
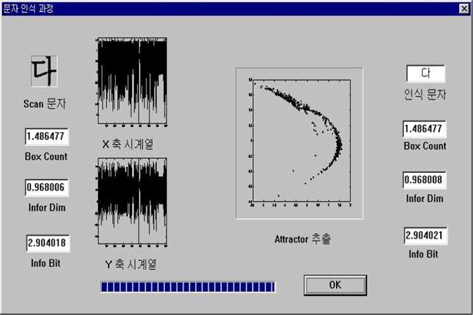
The calculated result of the fractal dimension is shown in Figure 6 and the character recognition process for the proposed system is shown in Figure 7.
This paper proposed a new method which extracts character features and recognizes characters using the fractal dimension of chaos theory which accurately recognizes minute differences with a strange attractor created with the Modified Henon system. This paper implements a high-precision character recognition system.
Conflict of Interest
No potential conflict of interest relevant to this article was reported.