악천후 시 항해하는 선박은 높은 파고로 인한 큰 진폭의 운동이 발생되며 이에 따라 선수 플레어, 선저 및 선미에서 자유 수면과의 충돌로 인한 슬래밍(Slamming) 현상이 발생한다. 또한 액체 화물을 운반하는 선박의 경우 파랑과 선박의 상대 운동에 의해 화물창 내에 슬로싱(Sloshing) 현상이 발생하며, 액체 유동에 따른 화물창 내벽에 슬래밍 현상이 발생한다. 이때 발생하는 큰 값의 슬래밍 충격 압력은 선체 구조에 대한 주요 손상 요인이 될 수 있다.
슬래밍 충격 압력에 대한 실험적 연구에 있어서 충격 압력의 크기에 영향을 주는 주요 변수는 경사각(Deadrise angle)과 입수 속도이다. 따라서 충격 압력과 입수 속도 및 경사각의 관계를 연구하는 것은 선체의 구조적 손상을 파악 및 예측을 위해 필수적이다.
과거부터 슬래밍 충격 압력에 대한 실험적, 이론적 연구를 진행하는데 있어 선체 단면과 유사하며 수학적으로 해석 가능한 쐐기 형상 모델이 많이 사용되어 왔다. 쐐기 형상은 쐐기 모서리의 각도 크기를 조절함으로서 다양한 단면의 선수 플레어 형상을 만들 수 있어 실제 선박의 근사 모델로 적합하고, 사상(Mapping) 기법을 통한 이론적 표현이 가능한 장점이 있다.
본 분야의 이론적 선행 연구로는 운동량 이론을 이용, 자유표면의 상승을 고려하지 않은 모델이 있다(Von Karrman, 1929). 이후 쐐기 형상을 평판으로 근사하고 퍼텐셜 이론을 적용한 연구가 진행되었다(Wagner, 1932). 또한 퍼텐셜 사상기법을 점근 해석(Asymtotic analysis)을 통한 접근 연구도 진행되었다(Logvinovich, 1969). 한편 선행연구에서 쐐기형상의 평판근사 단점을 개선하여, 퍼텐셜 이론을 평판으로 근사하지 않고 실제 쐐기 형상으로 근사(Schwarz-Christoffel mapping)하여 적용한 연구가 진행되었다(Zhao et al, 1996).
해당 내용과 관련된 실험적 선행 연구로는 강체로 간주된(탄성을 고려하지 않은) 평판(Chuang, 1966)과 쐐기(Chuang, 1967)에 대한 실험적 연구가 진행되었다. 자유 낙하한 수평 평판의 입수 시 발생하는 현상을 이론 및 실험적으로 연구하였다(Verhagen, 1967). 또한 공압 실린더(Pneumatic cylinder)를 이용하여강제 입수 현상을 재현한 강체의 슬래밍에 대한 연구가 진행되었다(Nahm, 2007). 또한 유탄성 효과를 고려하여 여러 가지 다른 두께의 평판의 거동에 대한 연구 또한 진행되었다(Shin, 2013). 탄성 금속 평판의 실험 수행을 통하여 유탄성 효과가 구조물의 거동에 미치는 영향에 대한 연구가 진행되었다(Park, 2012).
또한 다양한 각도의 쐐기 형상에 대한 실험을 진행하고, 입자 완화 유체동력학(Smoothed Particle Hydrodynamics)를 이용하여 수치해석과 비교한 연구 또한 진행되었다(Panciroli, 2012).
본 논문에서는 유탄성 효과가 고려된 쐐기 입수문제에 대해 입수 속도, 평판의 두께 변화에 대한 압력, 변형률을 계측하여 실험적 평가를 수행하였다.
자유낙하가 가능한 수송체(Transporter)에 부착된 시험체, 낙하 높이 및 경사각의 정의를 Fig. 1과 같다. 위의 노란색 부분은 수송체이고 밑의 회색 부분은 시험체이다. 낙하 높이는 시험체의 제일 낮은 점부터 수면까지의 높이로 정의하였다. 경사각은 시험체 밑면과 수평면으로 간주된 입수면 사이의 두 면이 이루는 각도로 정의하였다.
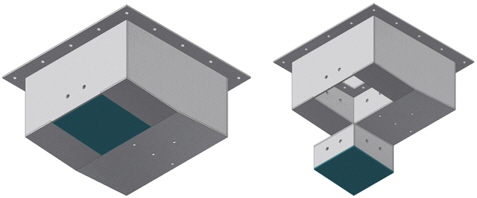
실험은 부산대학교 조선해양플랜트 글로벌핵심연구센터의 자유낙하 실험 장치를 통하여 수행되었다. 시험 장치의 제원은 1060mm × 630mm × 5445mm(L×B×H)이고, 최대 낙하 높이는 3.5m이다. 전자석을 이용하여 수송체를 들어 올렸다. 시험체의 치수는 600mm × 600mm × 200mm(L×B×H) 이다. 선형 운동 가이드 레일(Linear motion guide rail)을 통하여 수직 방향의 운동만 존재하도록 구속하여 자유낙하운동을 재현하였다. 시험체의 형상과 내부를 Fig. 2에 나타내었다.
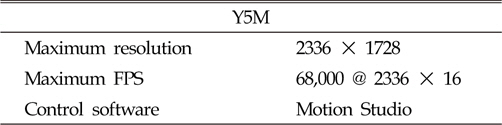
낙하 속도를 계측하기 위해 고속카메라를 사용하였다. 고속카메라로 촬영한 영상 중, 입수 직후의 사진을 Fig. 3에 나타내었다. 고속카메라의 제원은 Table 1에 나타내었다. 압력 및 변형률 데이터 취득은 각각 Kistler 701A, KYOWA KFEM-5-120 게이지를 사용하였으며, 주요 제원은 Table 2과 Table 3과 같다. 압력 신호와 변형률 신호는 모두 20kHz로 획득하였다.
[Table 1] Specification of high speed camera
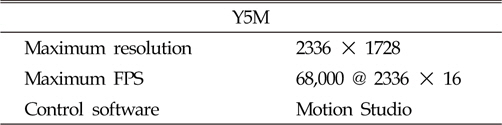
Specification of high speed camera
[Table 2] Specification of pressure gauge

Specification of pressure gauge
[Table 3] Specification of strain gauge

Specification of strain gauge
시험체는 Fig. 4와 같이 강체부분과 탄성체부분으로 나누어 구성되었다. 탄성체의 두께 변화에 따른 변형률 계측을 위해 교체 가능한 구조로 제작하였다. 파란색부분은 2mm 및 3mm 두께의 스테인리스강(SUS-304)으로 만들어진 탄성체이고, 회색 부분은 5mm 두께의 강철로 만들어져 강체로 가정하였다. 각각의 탄성체와 강체는 4면에 2개의 볼트를 사용하여 고정하였다.
실험 조건은 Table 4와 같고, 경사각은 4°, 탄성체의 두께는 2mm와 3mm이다.

Test matrix
낙하 높이는 0.25m부터 1.0m까지 0.25m 간격으로 실험을 수행하였다.
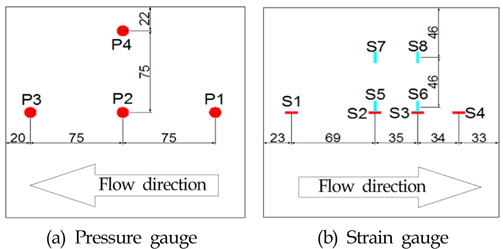
Fig. 5는 압력게이지와 스트레인게이지가 설치된 위치와 함께 유동 방향을 나타낸다. 압력게이지는 강체 부분에 부착하였고 스트레인게이지는 탄성체 부분에 부착하였다.
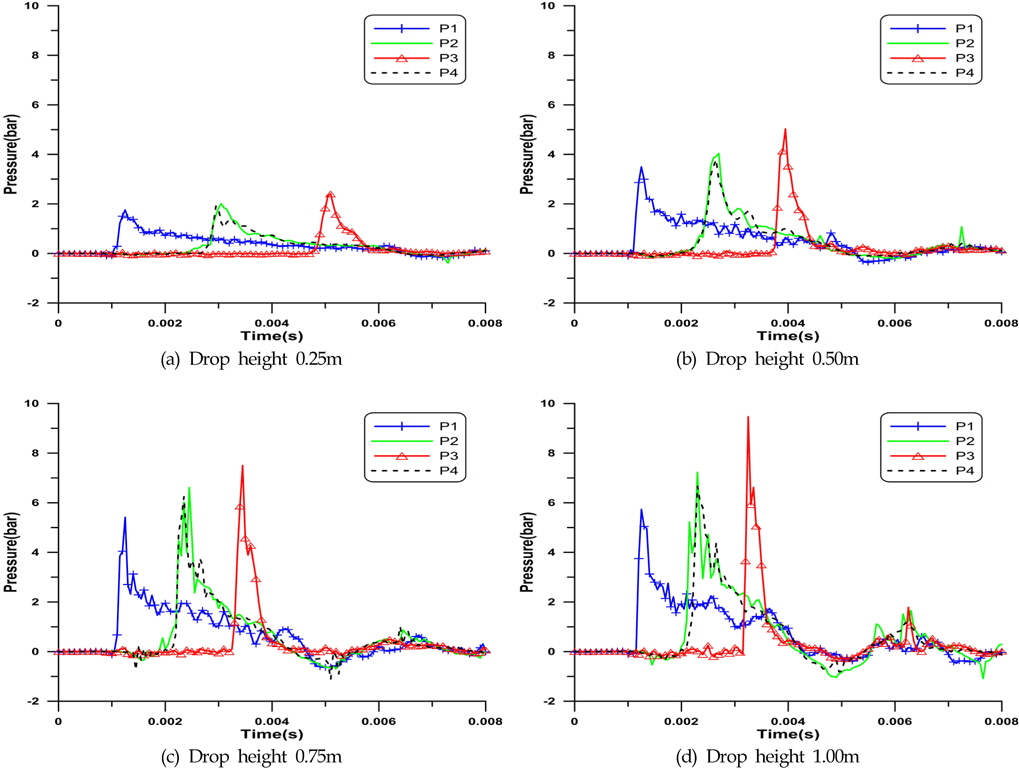
낙하 높이가 0.25m일 때의 측정된 압력의 크기를 Fig. 6(a)에 나타내었다. 최대 압력의 크기가 약 2.5bar이며 입수 직후 빠른 증가와 완만한 감소를 보이는 전형적인 충격 압력의 패턴을 보인다. 입수 직후 시험체의 표면에서 발생하는 유동이 시험체에 영향을 미치는 시간이 매우 짧고, 시험체가 입수할 때 부력을 충분히 받지 못하여 속도 변화가 거의 없었다. 따라서 자유낙하에도 불구하고 판 중심에서 유동 방향에 따라 압력 게이지의 순서와 동일하게 최대 압력값이 증가하여, 강제 낙하와 같은 경향을 보인다.
P4는 평판에서 유동 방향과 평행한 P1~P3의 계측선(Measuring line)과 수직한 방향에서 P2와 동일한 지점에 대한 압력값 변동 유무를 확인하기 위하여 설치한 참조 압력 게이지이다. 실제 실험 결과, P2와 P4는 압력 시계열의 경향이 유사한 사실을 확인하였다. 따라서 압력 분포가 2차원으로 간주 할 수 있다.
낙하 높이 0.5m, 0.75m, 1.0m에서의 압력 측정 결과를 Fig. 6 (b), (c), (d)에 각각 나타내었다. 낙하 높이가 0.25m일 때와 비교하여 압력의 크기가 커졌을 뿐, 전체적인 경향은 동일하게 측정되었다.
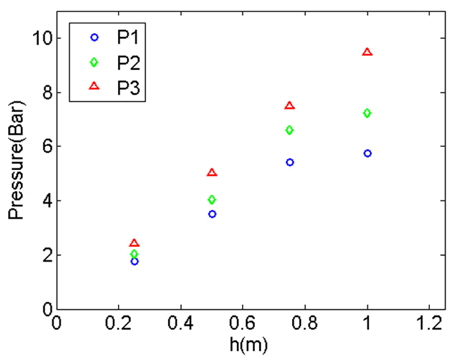
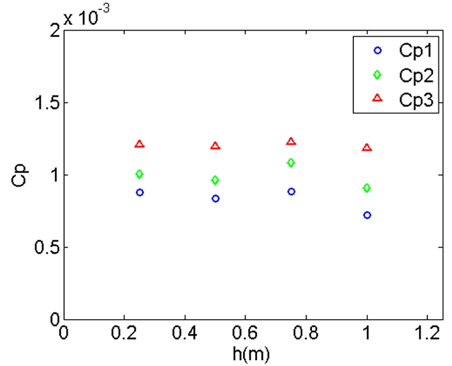
Fig. 7와 Fig. 8에 최대 압력과 압력 계수의 결과를 종합하여 나타내었다.
시험체 낙하 높이의 상승은 충격 압력 크기의 증가와 비례한다. Fig. 8에서 P3에서의 압력계수 표준편자는 1.7292✕e-5로 P1에서의 압력계수의 표준편차 7.6781✕e-5나 P2의 7.4400✕e-5보다 안정된 값을 보인다.
압력 계수 산정 시 사용 된 쐐기 모델의 낙하 속도는 고속카메라로 계측하였으며, 고속카메라는 2203 fps로 촬영하였다.
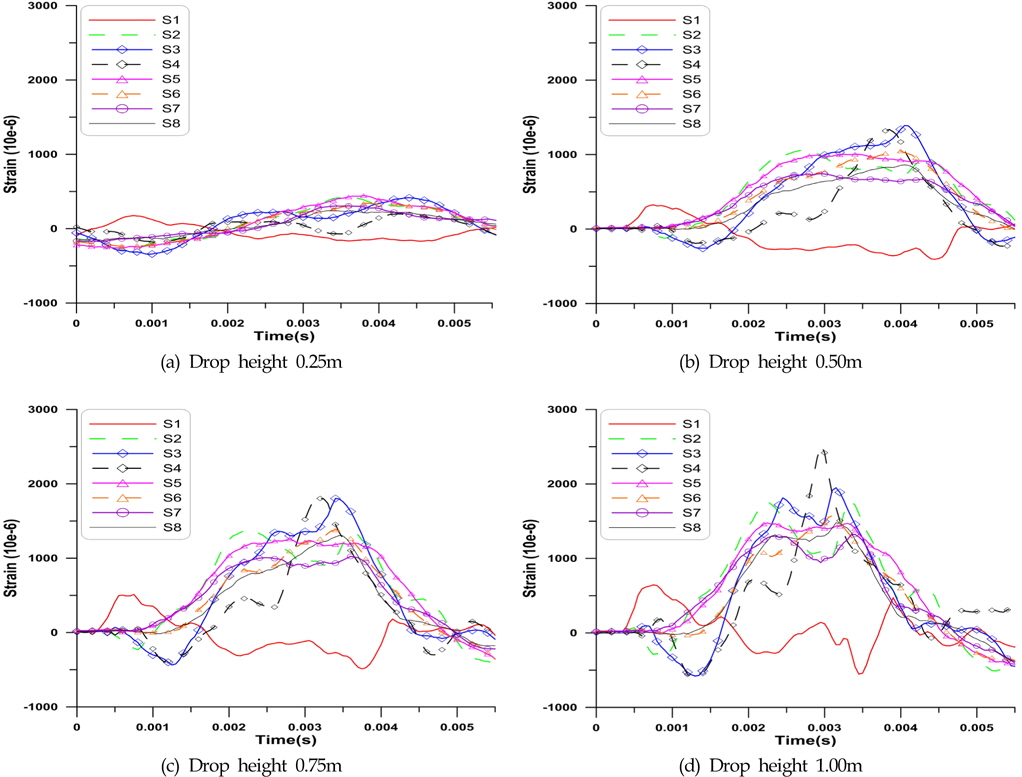
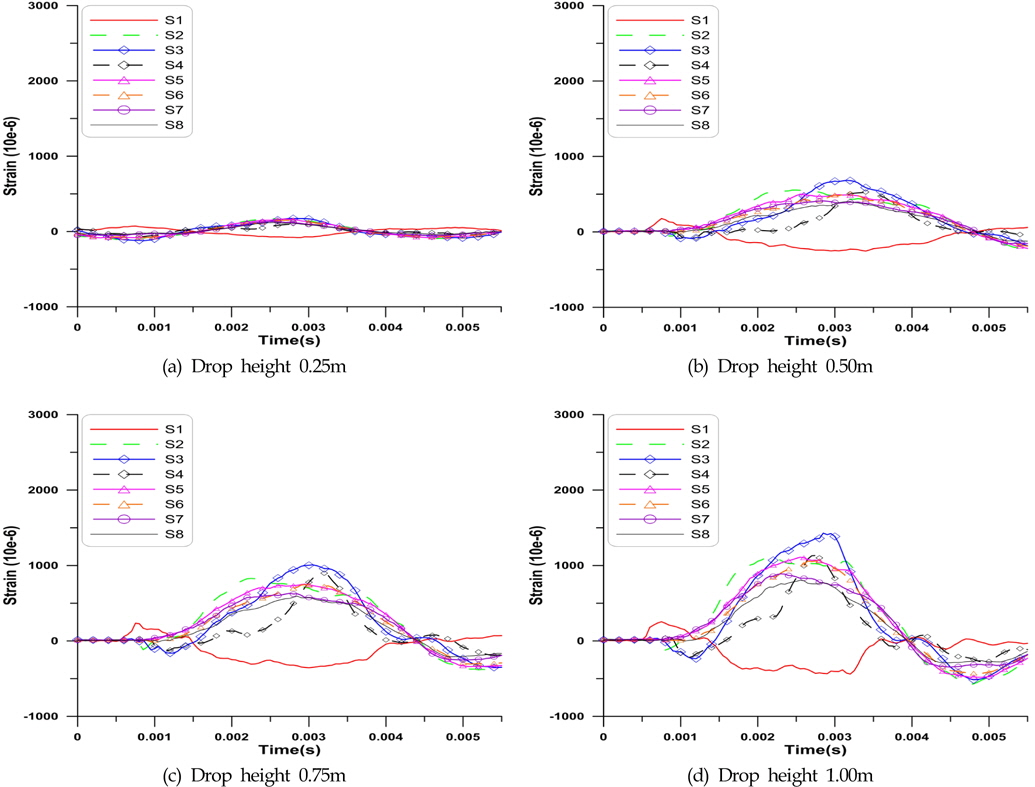
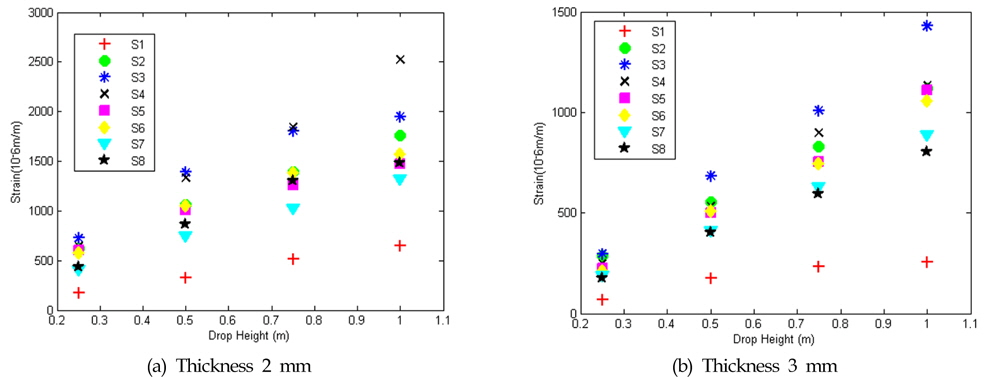
Fig. 9과 Fig. 10에는 각각 탄성체의 평판 두께 2mm, 3mm에 대해, 높이변화에 따른 변형률의 시계열 곡선을 나타내었다.
또한 Fig. 6 및 Fig. 7의 결과에 따라 최대 압력값이 유동 방향에 따라서 증가하기 때문에 최대 처짐값 또한 유동 방향에 따라서 증가한다.
Fig. 9 및 Fig. 10과 같이 최대 처짐이 S1 지점에서 발생할 때 S1에서의 변형률이 양수로 계측되었다. 측정된 최대 처짐이 S2, S3지점에서 발생하면 고정 경계조건에 의하여 경계와 23mm떨어진 가까운 위치의 S1은 변형률이 음수로 계측된다. 즉 S1 지점에서는 다른 스트레인 게이지에서 측정한 값과 반대의 경향을 보인다.
S4의 경우 고정 경계로부터 33mm 떨어진 지점에 위치하기 떄문에 S2, S3에 비해 변형률이 작아야 하지만, 시험체 제작 시 용접 품질에 의해 경계조건이 약해져 S2, S3 보다도 큰 값을 보인다. 같은 높이의 두께 2mm 결과에서 변형률의 최댓값이 두께 3mm 결과보다 지연되어 발생하는 현상을 확인할 수 있다. 최대 변형률을 종합하여 Fig. 11에 나타내었다. S1에 작용하는 압력의 최댓값이 가장 작기 때문에 S1의 변형률의 크기가 가장 작다.
스트레인 게이지 부착 위치에서 경계와의 거리 때문에 S7값은 S5값보다 작고, S8값은 S6값보다 작은 것을 확인 할 수 있다.
본 논문은 쐐기 입수 문제에서 유탄성 효과를 고려하기 위하여 낙하높이와 판 두께의 변화에 대한 유체 충격 압력과 판의 변형률을 실험적으로 계측하여 연구를 수행하였다.
(1) 낙하 높이가 높아지면 충격 압력의 크기가 증가한다.
(2) 유동방향과 수직한 방향의 변형률은 판의 중앙(S5 지점)에서 가장 크다.
(3) 유동방향과 평행한 방향의 변형률은 위쪽 반판(S3 근처)에서 가장 크다.
(4) 같은 높이일 때 최대 변형률의 지연 현상은 3mm 결과보다 처짐이 더 많이 발생하는 2mm 결과에서 나타난다.