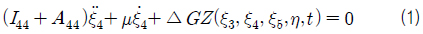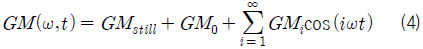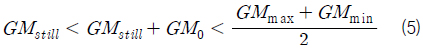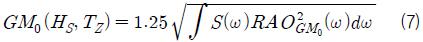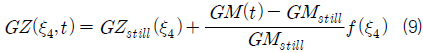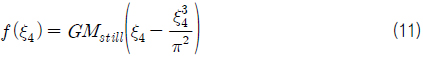선박의 운항 중 횡동요의 발생 및 크기는 선박의 안정성과 선원 및 승객의 승선감을 판별하는 중요한 지표이다. 특히 파라메트릭 횡동요(parametric roll)의 경우 선수파 또는 선미파에서 빠른 시간 안에 큰 횡동요 운동이 발생하므로 선체의 손상 또는 전복의 위험성을 야기할 수 있다. 실제로 1998년 발생한 Post-Panamax, C11급 APL CHINA 컨테이너선의 해양선박사고에서는 30° 이상의 횡동요로 인하여 적재 컨테이너의 2/3 이상이 파괴 및 유실되었다. 이 사건 이후 파라메트릭 횡동요 중선박의 동적 안정성을 분석하기 위한 연구와 이를 반영한 설계 및 운항 지침에 대한 규제 구축이 활발히 이루어져 왔다.

파라메트릭 횡동요의 기작(mechanism)은 파랑에 의한 수선면적의 변화, 즉 복원력의 변화가 횡동요를 가진시키는 과정으로 설명될 수 있다. 이에 대하여 Paulling and Rosenberg (1959)는 횡동요와 상하동요 또는 종동요 간에 연성된 비선형 복원력 성분을 도입하여 규칙파 중 파라메트릭 횡동요 발생을 수학적으로 분석하고 이를 실험을 통해 검증하였다. 유도된 횡동요 운동 방정식은 Mathieu equation 형태를 가지며, 해당방정식의 특성에 따라 횡동요 고유주기의 1/2배에 해당하는 입사파에서 파라메트릭 횡동요가 발생하는 것이 밝혀졌다. Roberts (1982)는 불규칙파 중 메타센터높이, GM 의 변화가 고려된 횡동요 운동 방정식의 안전성 판별 방법을 제시하여 파라메트릭 횡동요 발생을 분석하였다. 또한, Bulian, et al. (2004)는 파랑 중 복원력 변화의 비선형성을 실험에 근거하여 모델링함으로써 규칙파 또는 불규칙파에서 파라메트릭 횡해석시감범위동요의 발생뿐 아니라 크기를 예측하는 해석적 접근 (analytical model)을 도입하였다. 최근에도 국제해사기구 (International Maritime Organization, IMO)의 주도 아래 파라 메트릭 횡동요에 대한 규제를 구축하기 위해 복원력의 비선형성을 고려한 다양한 해석적 방법의 모델링이 수행 및 검증되고 있다 (IMO, 2010a; 2010b).

반면 파라메트릭 횡동요에 대한 수치해석의 적용으로서, Shin, et al. (2004)의 컨테이너선에 대한 랜킨패널법(rankine panel method) 도입과 Spanos and Papanikolaou (2007)의 어선에 대한 충격응답함수(impulse response function, IRF) 도입을 예로 들 수 있다. 또한 Park, et al. (2013) 역시 충격응답함수를 적용하여, 파라메트릭 횡동요에 대한 수치해석의 다양한 계산 인자들에 의한 불확실성 및 민감도를 파악하였으며, Kim and Kim (2011)은 GM 변분을 통한 모델링, 충격응답함수, 랜킨패널법을 단계적으로 적용하여 각 해석 방법의 특징을 비교, 분석한 바 있다.

파라메트릭 횡동요에 대하여 패널법 등과 같은 직접적 수치해석은 복원력의 비선형성을 엄밀히 고려할 수 있다는 장점이 있다. 하지만 파라메트릭 횡동요 현상의 비선형성으로 인하여 불규칙파 중 해석에는 결정적(deterministic) 접근인 아닌 확률적(stochastic) 접근이 요구된다. 즉, 다양한 해상 조건에 대해서 확률적 접근을 통해 통계적 특성을 판별하기 위해서는 긴 시간영역에 대한 계산이 수행되어야 하는데, 복잡한 수치적 접근의 적용은 계산시간의 비효율성을 야기한다. 특히, 이러한 직접 수치기법들의 적용에서는 파라메트릭 횡동요의 비선형 특성으로 인하여 시간영역에서의 해석이 불가피하다. 결국 여러 해양상태에 대한 파라메트릭 횡동요의 확률적 해석은 엄청나게 많은 수치해석의 비용과 노력을 요구하는 해석이 될 수 밖에는 없다. 본 연구는 이러한 수치해석의 노력을 줄이기 위하여, 비선형 복원력의 모델링을 통한 해석적 접근 기반의 효율적인 해석기법을 개발하고자 수행되었다.

본 연구에서는 종파(longitudinal wave) 중에서 대형 컨테이너선의 파라메트릭 횡동요 현상을 준해석적 방법을 통해 분석하였다. 이를 위하여 파랑 중 파면과 선박의 상하동요, 종동요에 따른 선박의 복원력 변화를 고려한 1.5 자유도 모델이 적용되었다. 횡동요의 진폭을 예측하기 위해 복원암(restoring arm), GZ 근사가 적용되었으며, 모델의 고도화를 위하여 파랑 중 GM 과 GZ 간의 관계를 분석하였다. 또한 GM 의 평균값 및 1차 조화성분에 대한 응답함수의 선형성을 이용하여 불규칙파 중에서의 파라메트릭 횡동요 해석이 수행되었다. 아울러, 본 연구를 통하여 개발된 해석기법의 결과들을 충격응답함수 기반의 약한 비선형(weakly nonlinear) 시간영역 해석 결과들과 비교함으로서, 해당 모델의 정확도와 효율성, 그리고 불규칙파 중 해석에서의 민감도 및 불확실성을 검증하였다.

종파 중의 1.5 자유도의 횡동요 운동방정식은 횡동요와 다른 운동간의 유체동역학적 연성은 대단히 약하다는 가정 하에 다음과 같이 표현할 수 있다.

여기서 I₄₄, A₄₄, Δ 는 각각 선박의 횡방향 관성모멘트, 부가관성모멘트, 그리고 배수량을 의미한다. ξ_i 는 i 번째 운동변위를 의미하는데, i가 3, 4, 5인 경우가 수직동요(heave), 횡동요(roll), 종동요(pitch)이다. 그리고, η 는 해양파의 변위이다. 즉, 식 (1)은 횡동요가 수직동요, 종동요, 자유표면의 변위에 영향을 받는다는 것을 의미한다. μ 는 횡동요에 작용하는 점성의 영향을 고려한 선형 감쇠계수로서 임계 감쇠의 γ의 비율을 가지는 값을 적용하였다.

여기서 A_44,∞ 와 C₄₄는 각각 무한주파수 부가관성모멘트와 복원력 계수를 의미한다. 일반적인 모형선 실험이나 실선의 경우 γ 는 3~10%의 값의 범위를 가진다고 볼 수 있다. 사실 점성으로 인한 횡동요 감쇠는 횡동요 각속도의 제곱에 비례하지만, 선박의 운동으로 인한 방사조파감쇠(radiation wave damping)는 통상 선형적으로 정의되고, 또한 식 (1)의 해석을 용이하게 하기 위하여 선형감쇠를 정의하는 것이 일반적인 방법 중 하나이다.

GZ 의 크기는 횡격사각의 크기뿐만 아니라 수선면적과 밀접한 관련이 있기 때문에 상하동요, 횡동요, 종동요 운동 및 해양파로 인한 수선면에 의해 결정된다. GZ 를 엄밀히 계산하기 위해서는 시간영역에서 선박과 η 간의 상대적인 위치를 반영하여 실제 침수면적에 작용하는 압력을 직접 적분해야 한다. 하지만 이러한 적분 과정은 큰 계산시간을 요구하기 때문에 파랑 중 GZ 변화에 대한 모델링을 통한 효율적인 준해석적 접근이 요구된다.

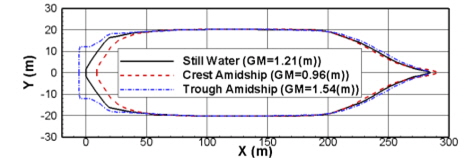
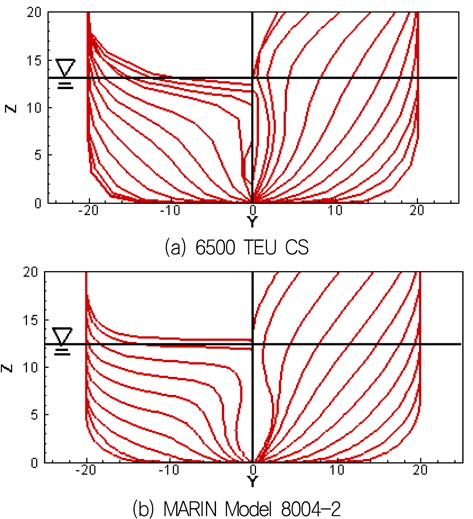
큰 선수 플레어(bow flare) 각과 트랜섬(transom) 선미를 가지는 컨테이너선의 경우 흘수에 따라 선수, 선미에서 수선면적이 급격하게 변화한다. Fig. 1의 예에서 알 수 있듯이 파정이 선체중앙부에 위치한 경우 작은 수선면적으로 인하여 작은 GM 을 가지게 되며, 반대로 파랑골이 선체중앙부에 위치한 경우에는 큰 수선면적으로 인하여 큰 GM 을 가지게 된다. 이는 파랑 중에서 선박의 횡방향 복원성능이 주기적으로 변함을 의미한다.

파랑 중 GM 의 변화를 근사하기 위해서는 파면에 대한 선박의 상대위치를 반영해야 하므로 충격응답함수 방법을 통해 계산된 종파 중의 상하동요, 종동요 운동을 대입하여 매 순간마다 실제 수선면적에 대한 GM 의 시계열을 식 (3)에 따라 계산한다.

여기서 IT 는 수선면적의 횡방향 이차모멘트, KG, KB 는 각각 선체바닥 기준 무게중심, 부력중심의 위치이다. 식 (3)에 따라 매시간 계산된 GM 의 시계열을 푸리에 변환(fourier transform) 하여 다음과 같이 GM 을 근사할 수 있다.

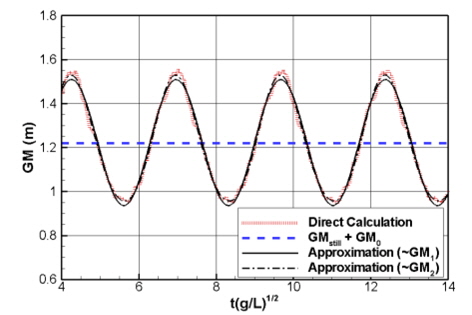
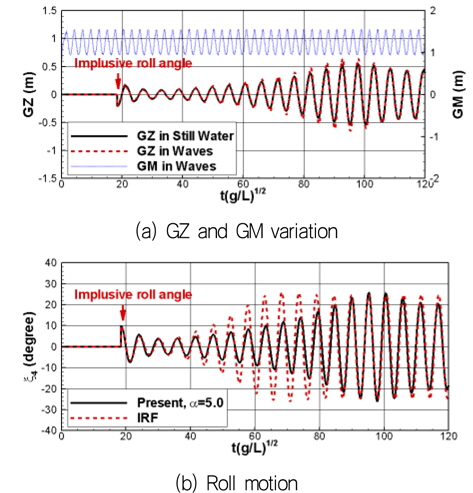
여기서 GM_still 은 정수 중에서의 GM이며, GM_i 는 i 차 조화성분을 의미한다. Fig. 2는 6,500TEU 컨테이너선에 대하여 파랑 중 직접 계산된 GM 의 시계열과 이를 근사한 결과의 예를 보여준다. 이 결과가 보여 주듯이 식 (4)의 조화성분들 중 1차 성분이 거의 대부분의 경우에서 가장 결정적 역할을 한다.

일반적으로 선박의 길이와 입사파의 파장이 유사할 때 (ω(L/g)^1/2≈2.5), 선체형상으로부터 파생되는 비선형성으로 인해 GM 은 최대값을 가지는 부근에서 가파르게 증가하였다 감소하는 경향을, 최소값을 가지는 부근에서는 완만하게 감소하다 증가하는 경향을 보인다. 따라서 파랑 중 GM 의 평균값을 결정하는 GM₀ 는 식 (5)의 관계를 가지며, 상대적으로 작은 값임에도 불구하고 파랑 중 선박의 정적 복원성능 (GM_still+GM₀)을 결정한다. 파라메트릭 횡동요 운동은 정적 복원성능에 대한 민감도가 강하기 때문에 (Park, et al., 2013), GM₀ 는 파라메트릭 횡동요의 발생 및 크기를 결정하는 중요한 인자이다.

GM₁ 은 파랑 중 복원성능의 변화량을 나타내는 인자로 파라메트릭 횡동요 발생 및 크기 결정에 가장 중요한 인자이다. 통상 입사파의 파장이 식 (6)에서 정의된 선박의 유효길이, L_EF 와 같을 때 파랑 중에 수선면적이 가장 크게 변화하고, 이때 GM₁ 은 최대값을 가진다.

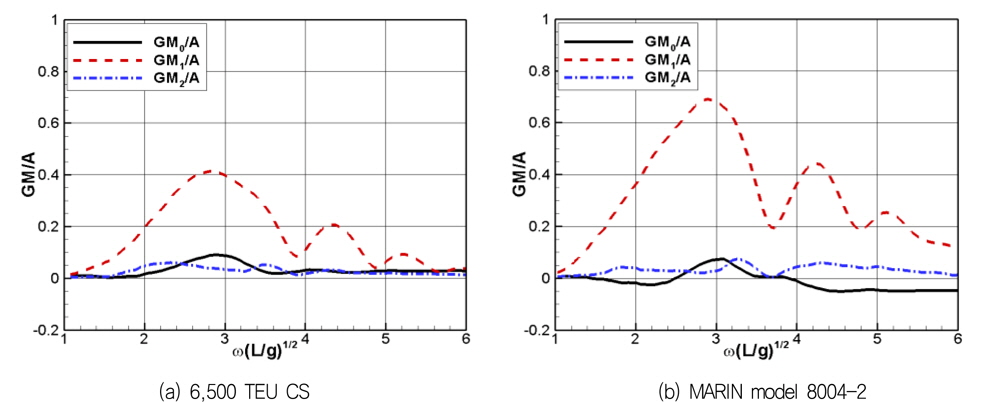
여기서 S_WL 은 수선면적, C_W 는 수선면적계수를 의미한다. 또한 입사파의 파장이 이 길이의 1/2n 배일 때 국부적 최소값을, 1/(2n+1) 배 일 때 국부적인 최대값을 가진다. 장파 영역에서는 선박의 운동에 복원력이 지배적으로 작용하여 파면과 선박의 상대 위치가 일정하게 유지되므로 GM₁ 은 0으로 수렴하며, 반대로 단파영역에서는 선박의 운동은 물론 파면에 의한 수선면적의 변화가 작기 때문에 마찬가지로 0으로 수렴한다. 이러한 GM₁ 의 특성은 Fig. 3의 GM 응답함수에서 확인할 수 있다.

GM₂ 이상의 고차 조화성분은 GM 의 시계열에 나타나는 비선형성을 나타내는 인자이지만 (Fig. 2), 그 값이 상대적으로 작고 파라메트릭 횡동요 발생의 기작에는 큰 영향이 없다. 따라서 파랑 중 GM 변화를 근사할 때에는 1차 조화성분까지만을 고려한다.

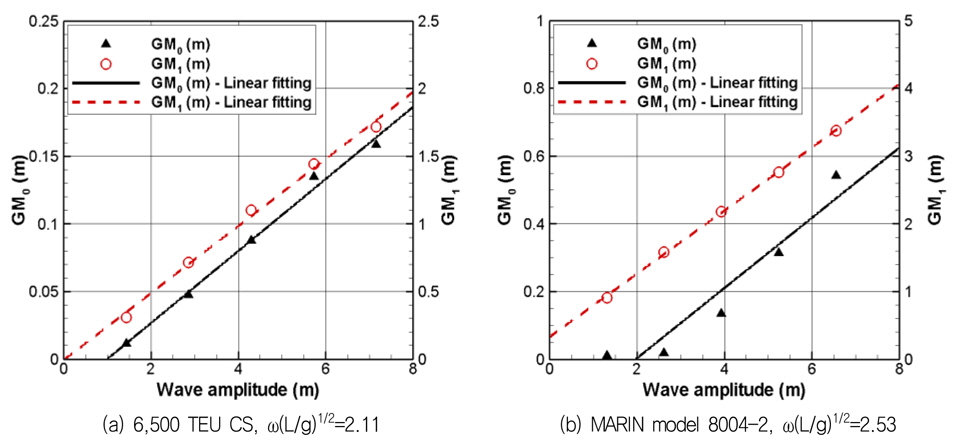
GM 응답함수의 선형성은 Dunwoody (1989a; 1989b)에 의해 제시되었다. Fig. 4는 앞서 적용된 6,500 TEU 컨테이너선에 대하여 GM₀ 와 GM₁ 응답함수의 선형성을 검증한 결과로, GM₁ 의 경우 해당 입사파의 조건 하에, 즉 선박의 길이와 입사파의 파장이 유사할 때 (ω(L/g)^1/2≈2.5), 파고에 대한 선형성이 확인되었지만 GM₀의 경우 약간의 비선형성이 확인되었다. GM 응답함수의 선형성은 불규칙파에서의 준해석적 방법 적용의 핵심이며, 각 응답함수의 선형성 및 GM₀ 가 Rayleigh 분포를 따른다는 가정 아래 불규칙파에서 파랑 중 GM 변화는 다음과 같이 근사할 수 있다.

횡동요 운동에 작용하는 비선형성 중 큰 횡격사각에서 복원력이 나타내는 비선형성은 파라메트릭 횡동요 운동의 크기 결정한다. 작은 횡경사각에서 GZ 의 크기는 GM 과 횡격사각에 비례하지만, 큰 횡격사각에서는 선체형상의 비선형성으로 인해 비선형 복원력이 작용하게 된다. 특히 컨테이너선의 경우 약 30° 이상에서는 갑판 침수로 인하여 복원력이 감소하게 된다. 이러한 GZ 곡선의 특징은 파랑 중에서도 유지되며, 따라서 파랑 중 GZ 를 식 (9)와 같이 근사할 수 있다.

여기서 GZ_still 은 정수 중의 GZ 의 크기, f(ξ₄)는 파랑 중 GM 의 변분과 GZ 의 변화간의 관계를 나타내는 함수(GZ factor function)이다. 즉 파랑 중 GZ 는 정수 중 GZ, 그리고 파랑 중 GM 의 변분과 정수 중 GM 간의 비를 통해 근사되었다.

대변위 운동인 파라메트릭 횡동요의 크기를 예측하기 위해서는 복원력의 비선형성을 반영할 수 있도록 f(ξ₄)를 어떻게 모델링 하느냐가 중요하다. Belenky와 Umeda에 의해 제시된 f(ξ₄)의 모델링은 각각 식 (10), (11)과 같다 (IMO, 2010a; 2010b).

여러 선박에 대한 계산 경험을 바탕으로 본 연구에서는 아래 식과 같이 f(ξ₄)에 대한 식을 제시한다.

여기서 α 는 고차항의 차수를 결정하는 값이며, ξ_4,max 는 정수 중 GZ 곡선에서 복원력의 크기가 0이 되는 횡경사각을 의미한다. 특히 α 는 큰 횡경사각에서의 f(ξ₄)의 크기를 결정하는 값이며, 이에 따라 파랑 중 GZ 변화의 크기를 조절할 수 있다. Song의 방법 (Song, et al., 2013)에서는 α 를 3.0으로 고정하였지만, 본 방법에서는 변수로 설정하고 각각의 선형에 대한 검증을 통해 이 값을 결정하였다.

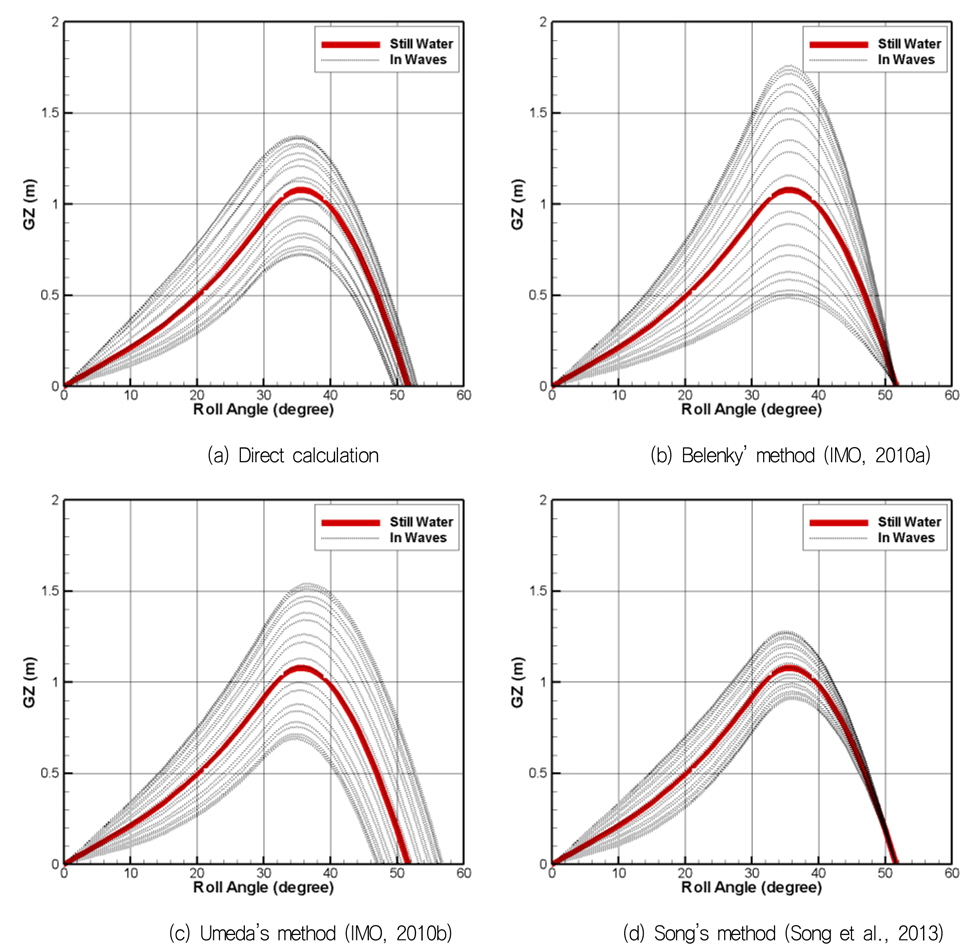
Fig. 5는 파면에 대한 정적 평형을 가정하고, 실제 침수면적에 대한 압력 적분을 수행하여 파랑 중 GZ 곡선을 직접 계산한 결과와 각각의 근사 방법을 통해 계산한 결과를 나타낸 것이다. 직접 계산된 결과와 비교하였을 때 파랑 중 GZ 의 변화를 Belenky의 방법 (IMO, 2010a)은 다소 크게, Song의 방법 (Song et al., 2013)은 다소 작게 예측하는 것을 알 수 있다. Umeda의 방법 (IMO, 2010b)의 경우, 횡경사각이 작은 경우에는 GZ 의 변분이 직접 계산된 결과와 비교적 잘 일치하지만, 30° 이상의 큰 횡격사각에서 횡격사각이 증가함에 따라 GZ 의 변분이 감소하는 경향을 나타내지 못하는 것을 알 수 있다. 실제로 직접 계산된 결과에 따르면 큰 횡경사각에서는 파랑에 의한 수선면적의 변화가 감소하여 GZ의 변분이 복원력의 크기와 함께 감소하는 것을 확인할 수 있다.

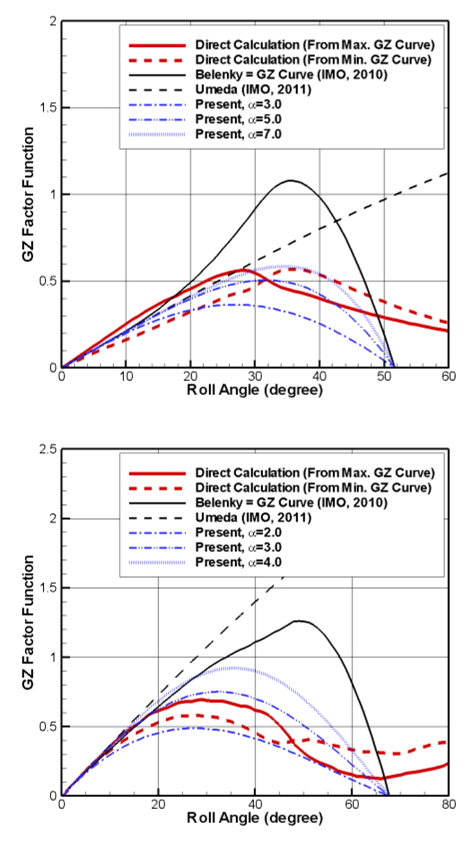
근사 방법의 정확도를 엄밀히 관찰하기 위하여 직접 계산된 파랑 중 최대, 최소 GZ 곡선을 통해서 를 역으로 계산한 후, 이를 각 모델링 방법과 비교하였다 (Fig. 6). 직접 계산된 는 횡경사각이 증가함에 따라 선체형상으로부터 파생되는 비선형성을 나타내며 단순한 모델링을 통해 이를 완벽하게 고려하기에는 한계가 존재한다. 하지만 파라메트릭 횡동요의 범위 (0°~40°)에 대해서 식 (12)에 적절한 α를 대입하였을 때 (6500 TEU 컨테이너선: α=5.0, MARIN model 8004-2: α=2.0~3.0), 가 직접 계산된 결과와 유사하였다. 두 선형에서 α 값이 다른 이유는 선수, 선미 형상의 차이로 인하여 파랑 중 수선 면적 변화의 크기, 즉 GM₁ 의 크기가 다르기 때문이다 (Fig. 3). 따라서 α 는 각각의 선형에 대하여 직접 계산된 결과와의 비교를 통해 적절한 값이 선택되어야 한다.

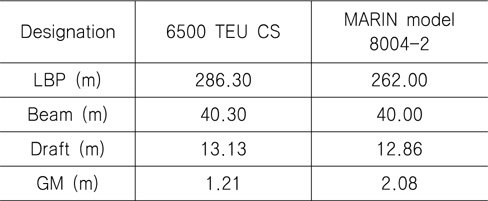
준해석적 방법의 적용 및 수치계산을 위한 해석 모델로 파라메트릭 횡동요에 민감한 컨테이너선인 6500 TEU 컨테이너선과 MARIN model 8004-2 선종을 선택하였다. Table 1은 해당 선형들의 주요 치수를, Fig. 7은 선도를 나타낸 것이다. 두 선박은 크기가 유사하지만 GM 및 선수, 선미 형상에서 약간 차이가 있다.

앞서 설명한 준해석적 방법에 대한 검증을 위하여 충격응답함수 (IRF) 기반의 수치해석을 파라메트릭 횡동요 해석에 같이 적용하여 그 결과를 비교하였다. 준해석적 방법에서는 식 (1)의 1.5 자유도 횡동요 운동방정식에 4차의 Runge-Kutta 방법을 적용하였으며, 반면 IRF 기반의 수치해석의 경우 Cummins (1962)에 의해 제시된 기법에 대하여 스트립 이론인 STF 기법 (Salvensen, et al., 1970)을 통해 계산된 유체동역학 계수를 도입하였다. 특히, IRF 기반의 수치해석에서는 실제 접수면 (wetted area)에서의 비선형 Froude-Krylov 힘과 비선형 복원력이 고려된 약한 비선형(weakly nonlinear) 선박운동해석을 수행하였다. 충격응답함수의 파라메트릭 횡동요에 대한 해석기법 및 검증은 Kim and Kim (2011)에서 확인할 수 있다.

부가적인 사항으로, 식 (2)의 횡동요에 대한 점성 감쇠계수는 두 방법 모두에서 동일하게 적용되었다. 또한 선수파 중에 운항하는 선박에서 발생하는 풍하중, 조류 등에 의한 일시적인 횡경사각을 시뮬레이션에서는 특정 시간에 특정 값을 선박 운동에 부여하는 방식으로 모델링하였으며 (Fig. 8), 전진 속도는 두 선박 모두에 대하여 5 (knots)로 선정하였다. 해당 조건하에 준해석적으로 계산된 파라메트릭 횡동요 운동의 특성을 충격응답함수법 결과와 비교하여 본 연구에서 제시된 모델링 방법을 검증하였다.

규칙파 중에서 파라메트릭 횡동요는 일반적으로 입사파의 주기가 횡동요 고유주기의 1/2배 부근일 때 발생한다. 이런 조건에서는 횡동요 발생 시기와 수선면적의 증가 시기가 일치하여 복원력이 정수 중보다 파랑 중에서 증가하기 때문에 횡동요 운동이 점차 가진되어 파라메트릭 횡동요가 발생한다. 그리고 파라메트릭 횡동요가 발생한 이후에는 수선면적 변화에 따른 유체력의 변화와 횡경사각 증가에 따른 감쇠력 등이 횡동요 가진력과 균형을 맞추면서 횡동요 운동이 발산하지 않고 일반적으로 준정상상태(quasi-steady state)를 유지한다.

이러한 파라메트릭 횡동요의 기작은 식 (12)의 준해석적 방법을 적용한 결과인 Fig. 8에서 확인할 수 있다. 계산된 횡동요 운동을 충격응답함수법의 결과와 비교해보면, 초기 횡경 사각으로부터 횡동요가 가진되는 구간에서는 오차가 발생하지만 준정상상태에서는 횡동요 운동의 주기 및 크기가 비교적 잘 일치하는 것을 확인할 수 있다.

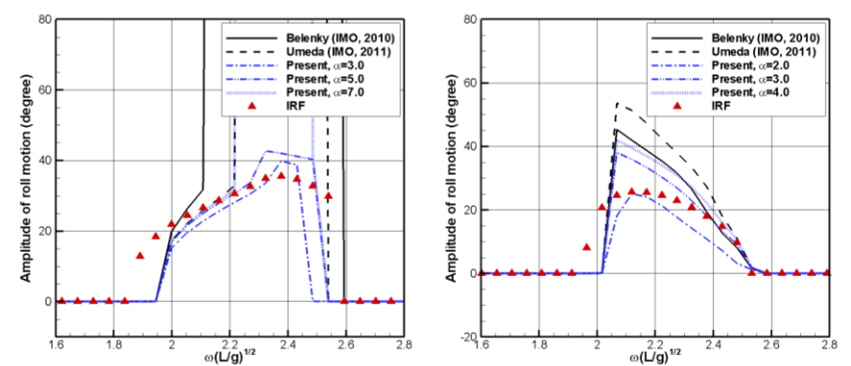
Fig. 9는 식 (10)~(12)의 준해석적 방법과 충격응답함수를 통해 계산한 규칙파 중 파라메트릭 횡동요 운동을 나타낸 것이다. 파라메트릭 횡동요가 발생하는 입사파 주파수의 영역과 준정상상태에서 횡동요 응답의 크기는 두 방법간에 약간 차이를 보인다. 이러한 차이의 원인은 부가질량, Froude-Krylov 힘 등 유체동역학적 힘과 파랑 중 비선형 복원력에 대한 계산 방법의 차이에서 찾을 수 있다. Belenky의 방법 (IMO, 2010a)의 경우 파랑 중 복원력의 변화를 과도하게 예측하여 일정 이상의 횡경사각 이후에서 횡동요 운동이 발산하였다. Umeda의 방법 (IMO, 2010b) 역시 횡경사각이 증가함에 따라 파랑 중 복원력의 변화가 감소하는 경향을 고려하지 못하므로 횡동요 운동을 과도하게 예측하였다. 반면 식 (12)의 α 값에 2절에서 검증된 값을(6500 TEU 컨테이너선: 5.0, MARIN model 8004-2:2.0~3.0) 대입하여 계산한 결과에서는 충격응답함수법의 결과와 같이 횡동요 운동이 모든 주파수 영역에서 발산하지 않고 준정상상태를 가지는 것을 확인할 수 있다. 또한 40°에 가까운 큰 횡동요 응답이 발생하는 경우를 제외하였을 때, 모든 주파수 영역에서 파라메트릭 횡동요의 발생 및 크기의 경향이 충격 응답함수법의 결과와 유사함을 알 수 있다. 따라서 수치해석 수준의 준정상상태의 응답 예측을 위해서는 큰 횡경사각에서의 비선형 복원력에 대한 모델링의 고도화가 요구된다.

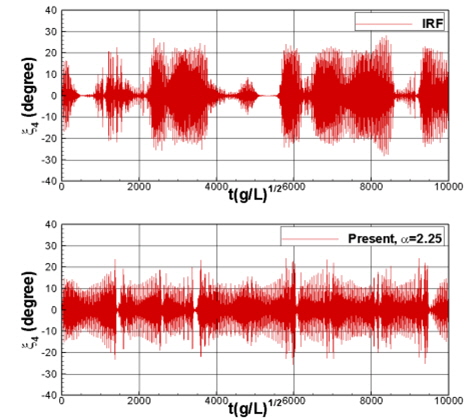
실제 해상 상태에 대하여 파라메트릭 횡동요를 예측하기 위해서는 불규파에서의 실험 및 수치해석이 수행되어야 한다. Fig. 10은 충격응답함수법과 준해석적 방법을 통해 계산된 불규칙파 중 파라메트릭 횡동요의 예를 보여준다. 특정 시간 구간에서는 횡동요가 거의 발생하지 않으나, 또 다른 시간 구간에서는 20°가 넘는 횡동요가 발생하는 것을 알 수 있다. 또한, 충격응답함수법과 준해석적 방법이 각 시간 구간에서 명확하게 다른 방식으로 횡동요의 발생 및 크기를 예측하는 것을 확인할 수 있다. 이러하듯 불규칙파 중 파라메트릭 횡동요는 강한 비선형성을 동반한 대변위 운동이기 때문에 서로 다른 방법을 통해 계산된 횡동요 시계열간의 직접적 비교에는 한계가 있다. 따라서 비선형 시스템인 파라메트릭 횡동요의 불규칙파중 통계적 특성을 파악하기 위해서는 결정론적인 과정이 아닌 반복계산을 통한 확률론적 접근을 필요로 한다.

준해석적 방법을 통한 불규칙파 중 파라메트릭 횡동요 예측을 검증하기 위해 국제수조회의(ITTC)의 Special Committee on Stability in Waves에 의해 수행된 파라메트릭 횡동요에 대한 비교 연구 (Reed, 2011)의 계산 조건을 도입하였다. 해당 연구에서는 MARIN model 8004-2 선형에 대해서 불규칙파 중 파라메트릭 횡동요 실험을 수행하고, 얻어진 횡동요의 통계적 특성을 각 기관의 계산 결과와 비교하였다. 본 연구에서 적용된 계산 조건은 유의파고(Hs)가 5.25 m, modal period(Tp)가 14.4초인 선수파이며, 해당 스펙트럼은 80개의 성분파로 이산화되었다. 또한 각 성분파의 위상을 다르게 하여 20번의 계산을 수행함으로써, 파라메트릭 횡동요의 통계적 특성을 파악하고자 하였다.

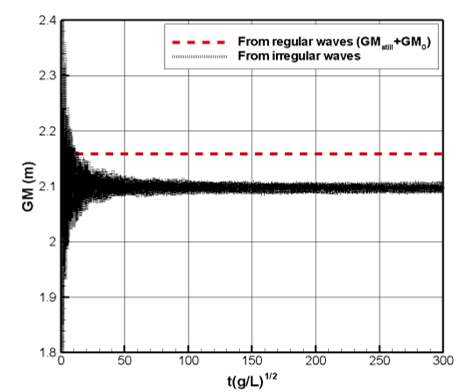
파라메트릭 횡동요 시뮬레이션에 앞서 GM 응답함수의 선형성에 대한 가정으로부터 도출된 식 (7), (8)을, 충격응답함 수법을 이용하여 계산한 불규칙파 중 GM 의 변화를 분석하여 우선 검증하였다. Fig. 11에 따르면 불규칙파 중 GM의 평균 값은 30분 이내의 시뮬레이션에서 일정 값으로 수렴하는 것을 확인할 수 있다. 하지만 수렴된 평균값은 GM₀ 응답함수를 식 (7)에 대입하여 계산한 GM₀ 에 정수 중 GM 값을 더한 값과는 약 3%의 차이를 보인다. 이는 선박의 길이와 입사파의 파장이 비슷하지 않은 경우에 대해서 GM₀의 선형성에 대한 가정에 한계가 있음을 나타낸다. 불규칙파 중 파라메트릭 횡동요의 발생은 정적 복원성능 (GM_still+GM₀)에 대한 민감도가 매우 강하기 때문에 식 (7)에 의한 준해석적 방법의 적용은 파라메트릭 횡동요 예측에서 오차를 야기할 수 있다.

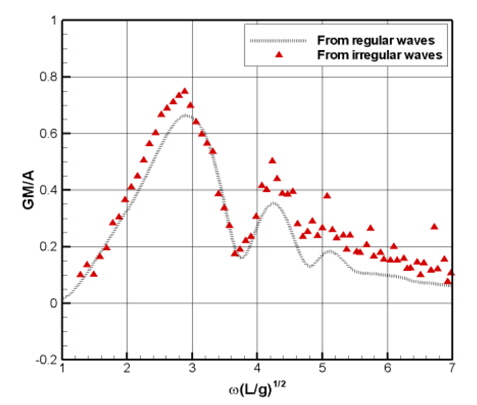
Fig. 12는 불규칙파 중 GM 의 시계열을 푸리에 변환하여 얻은 GM₁ 응답함수와 규칙파 조건하에 계산된 GM₁ 응답함수 (Fig. 3)를 나타낸 것이다. 두 응답함수와 그 크기와 경향이 유사한 것을 확인할 수 있으며, 이는 GM₁ 응답함수의 선형성에 대한 가정을 뒷받침한다. 하지만 파라메트릭 횡동요의 발생과 크기에 큰 영향을 끼치는 주파수 영역에서 (ω(L/g)^1/2≈2.0~3.0)에서 불규칙파로부터 계산한 GM₁ 의 응답이 약간 큰 것을 확인할 수 있으며, 이는 저주파수 영역의 입사파 성분에 의해 발생한 고차 조화성분의 기여로 판단된다. 이러한 GM₁ 응답의 차이는 파라메트릭 횡동요 크기 예측에서 준해석적 방법과 충격응답함수법간에 차이를 발생시킬 수 있다.

준해석적 방법과 충격응답함수법을 적용하여 위에서 설명한 불규칙파 조건에 대한 파라메트릭 횡동요 시뮬레이션을 수행한 후, 횡동요의 분산 및 95% 신뢰도 구간을 계산하였다. 준해석적 방법의 적용 시 식 (12)의 α 에는 앞서 MARIN model 8004-2 선형에 대하여 검증된 값 (α≈2.0~3.0) 중에서 2.25를 대입하였다. 또한 식 (2)의 횡동요에 작용하는 선형 감쇠계수는 비교 연구 (Reed, 2011)에서 수행된 free roll decay test와의 비교를 통해 γ 를 결정하여 준해석적 방법과 충격응답함수법 모두에서 동일하게 도입하였다.

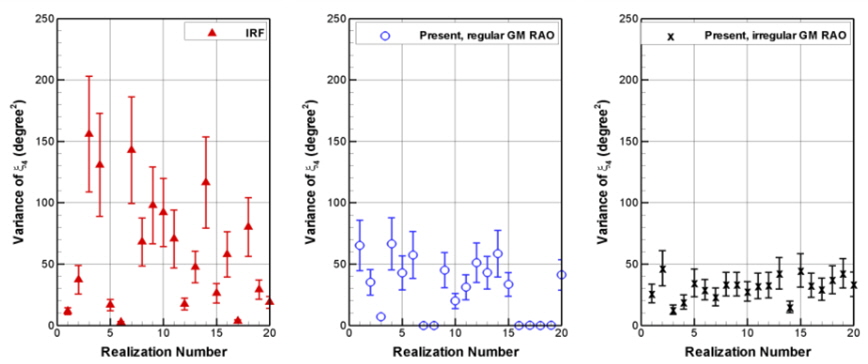
Fig. 13에 따르면 각기 다른 위상을 가지는 20개의 불규칙파에 대해서 2,500초의 시뮬레이션을 수행하였을 때 충격응답 함수법은 준해석적 방법과 비교하여 성분파의 위상에 대한 강한 민감도를 보이며, 강한 불확실성에 따라 넓은 신뢰도 구간이 나타나는 것을 알 수 있다. 반면 규칙파 계산으로부터 얻어진 GM 응답함수를 도입하여 준해석적 방법을 적용하였을 때에는 일부 계산에서 파라메트릭 횡동요가 발생하지 않는 것을 확인할 수 있었으며, 이는 식 (7)에 의해 계산된 GM₀ 의 오차로 인하여 변화된 선박의 정적 복원성능이 파라메트릭 횡동요 발생을 저하시킨 것으로 판단할 수 있다. 불규칙파 시뮬레이션을 통해 계산된 GM 응답함수를 적용하였을 때에는 모든 경우에 대해서 충격응답함수법과 마찬가지로 파라메트릭 횡동요가 발생하였으며, 분산 및 신뢰도 구간이 각 시뮬레이션마다 유사한 값을 보였다. 준해석적 방법에서 파성분에 대한 민감도가 낮은 이유는 약한 비선형 선박운동해석과는 달리 파랑 중 GM 변화를 평균값과 1차 조화성분만을 이용하여 근사하였기 때문이다.

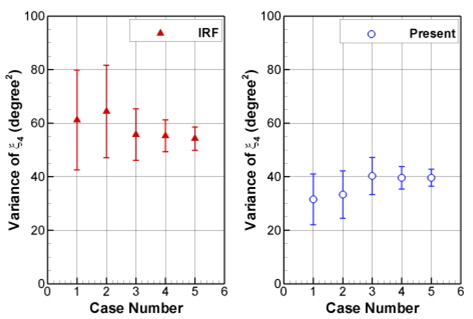
Fig. 14는 불규칙파 시뮬레이션으로부터 얻은 GM 응답함수를 적용한 준해석적 방법과 충격응답함수법의 해석시간범위 (time-window)에 대한 민감도를 나타낸 것이다. 두 방법 모두 해석시간범위가 길어짐에 따라 횡동요의 분산이 일정 값으로 수렴하는 동시에 신뢰도 구간이 점차 좁아지는 것을 확인할 수 있다. 충격응답함수법의 경우 짧은 해석시간범위에서는 넓은 신뢰도 구간, 즉 큰 불확실성을 보이기 때문에 긴 시간의 시뮬레이션을 요구하는 반면, 준해석적 방법은 짧은 해석시간 범위에 대해서도 낮은 불확실성을 보이는 것을 확인할 수 있다. Fig. 15는 ITTC 비교 연구 (Reed, 2011)에서 수행된 실험 및 계산 결과와의 비교를 나타낸 것으로, 각각의 방법으로 계산된 횡동요의 분산간에는 차이가 존재한다. 이는 유체동역학적 힘과 비선형 복원력에 대한 계산 방법의 차이에서 그 원인을 찾을 수 있다. 본 연구의 준해석적 방법을 통해 계산된 분산은 실험 결과와 유사하며, 다른 계산 방식들에 비하여 신뢰도 구간이 좁아 불확실성이 낮은 것을 확인할 수 있다.

준해석적 방법의 파성분과 해석시간범위에 대한 낮은 민감도는 공학적 적용 관점에서 주어진 해상 조건에 대한 파라메트릭 횡동요의 특성을 큰 불확실성 없이 제시할 수 있다는 측면에서 유용하다. 그럼에도 불구하고 비선형 시스템의 특성상 발생하는 계산인자에 대한 강한 민감도 및 불확실성에 의해 불규칙파 시뮬레이션은 반복계산이 요구되며, 이에 따라 계산시간 측면의 효율성은 중요한 문제로 대두된다. 80개의 성분파를 이용한 24시간의 해석시간범위에 대하여 충격응답함수법은 Intel i5-750/2.66 @GHz CPU에서 약 4시간의 계산시간을 요구하는 반면, 준해석적 방법을 통한 계산은 약 2분의 계산시간을 필요로 한다. 따라서 준해석적 방법을 통한 효율적인 시뮬레이션은 계산인자로부터 파생된 불확실성을 고려하여 파라메트릭 횡동요의 통계적 특성을 파악하는 데 용이하다. 또한 다양한 해상조건 중 심각한 파라메트릭 횡동요가 발생하는 조건을 선별하여 수치해석 적용의 기준을 마련할 수 있다는 점에서 준해석적 방법의 효용성이 존재한다.

본 연구에서는 종파 중 컨테이너선의 파라메트릭 횡동요 해석에 준해석적 방법을 적용하여 그의 정확도 및 효율성을 충격응답함수법 결과와 비교하여 검증하였다. 해석 결과로부터 다음의 결론을 제시하고자 한다.

· 모델링된 준해석적 방법의 정확도는 파랑 중 GZ 변화에 대한 근사에 크게 의존한다는 것을 확인하였으며, 존재하는 몇 가지의 준해석적 해석기법들과 비교하여 본 연구에서 제시된 방법이 충격응답함수법과 비교하여 그 결과가 유사하였다. · 큰 횡경사각에서의 비선형 복원력에 대한 정확한 근사에는 한계가 존재하며, 이는 규칙파 또는 불규칙파에서 파라메트릭 횡동요의 발생 및 크기 예측의 오차로 귀결되었다. · GM 응답함수의 선형성 가정에 일부 한계가 있음을 확인하였으며, 이는 불규칙파 중 파라메트릭 횡동요 예측에서 오차를 발생시킬 요인이 될 수도 있음이 관찰되었다. 특히, 불규칙파 중 GM0 예측은 선형성 가정이 아닌, 불규칙파 중 시뮬레이션 등 다른 방법이 요구되었다. · 불규칙파 중 파라메트릭 횡동요 예측에서 준해석적 방법은 충격응답함수법과 비교하여 해석시간범위와 스펙트럼의 성분파에 대한 민감도가 비교적 약하게 나타났으며, 이는 공학적 적용 관점에서 주어진 해상 조건에 대한 파라메트릭 횡동요의 특성을 큰 불확실성 없이 제시할 수 있다는 것을 의미한다. · 파라메트릭 횡동요 예측에 있어 준해석적 방법의 적용은 계산시간측면에서 효용성이 있으며, 향후 횡동요 크기 예측에 대한 정도를 높이기 위해서 큰 횡경사각에서의 비선형 복원력 모델링의 고도화에 대한 연구가 필요하다.