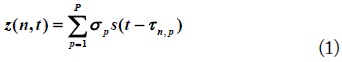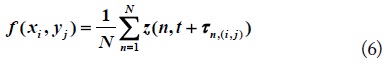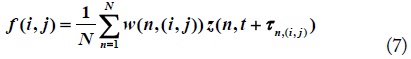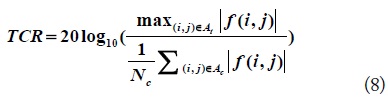Through-the-wall radar imaging (TWRI) is an emerging area of research and development dealing with ‘seeing’ the target behind the wall. There have been many studies on TWRI. Some have focused on TWRI system architecture [1], while others have investigated signal processing issues related to TWRI [2–4]. To make the system more complete, however, suitable reconstruction of the radar scene is indispensable. Various reconstruction algorithms have been developed to process TWR measurement data. Several of these are based on beamforming or beam-space multiple signal classification (MUSIC) [5], while others cast the TWRI problem as an inverse scattering problem [6,7]. Among the reconstruction algorithms, a delayed-sum (DS) algorithm is widely used because of its algorithmic simplicity and robustness [8]. The conventional DS algorithm uses only the range information of measured data, although the TWR antenna has its own radiation pattern.

In this paper, the synthetic and experimental results of TWRI are presented using a radiation pattern-based DS algorithm. We assume that wall clutter is adequately removed using the subspace projection method. Images are evaluated using the target-to-clutter ratio (TCR), which is widely used in synthetic aperture radar (SAR). This paper shows that a radiation pattern-based DS algorithm shows higher TCR compared to the conventional DS algorithm.

This paper is organized as follows: in Section II, we present the basic theory of TWRI. Then, Sections III and IV deal with the simulation and experiment results. Finally, a conclusion is presented in Section V.

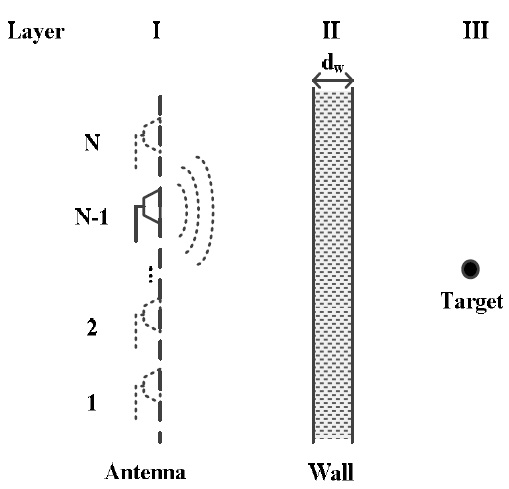
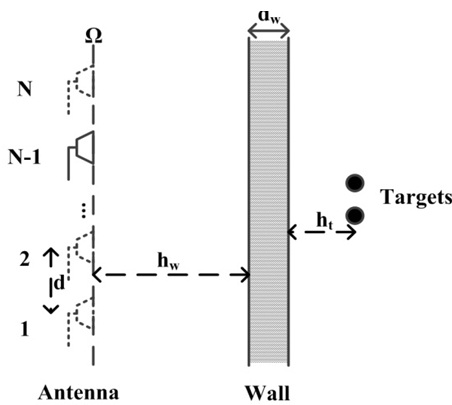
We apply SAR signal modeling for TWRI, as depicted in Fig. 1. The second layer is a wall with thickness represented by d_w and permittivity by ԑ_w. The first and third layers are free space. We assume a monostatic radar case, and N antennas are uniformly spaced parallel to the wall. For P point targets, due to the targets only, the signal received at the nth antenna is given by [8],

where s(t) is the transmitted signal convolved with the two-way transfer function of the wall, σ_p is the reflection coefficient of the pth target, and τ_n,p is the two-way traveling time between the nth antenna and the pth target.

In TWRI, strong reflections from the wall often cause the target signal to become obscured. There are various methods of mitigating such wall clutter [2–4]. In this paper, we adopt the subspace projection method. This is based on the fact that the most significant terms of signal spectrum are dominated by the wall clutter. A received signal matrix, Z, can be factorized using singular value decomposition (SVD) as:

U = [u₀, u₁, ... , u_N-1] and V = [v₀, v₁, ... , v_M-1 ] are unitary matrices containing the left and right singular vectors, and Λ is an [M, N] diagonal matrix containing singular values in decreasing order. H denotes Hermitian. If wall clutter is spanned by the first p singular vectors, the clutter can be removed by projecting the signal matrix on the remaining singular vectors, i.e.,

with

where e_target and I is the wall clutter removed from the data matrix and identity matrix, respectively [2].

A DS algorithm is a simple and robust image reconstruction algorithm for TWRI. The ijth pixel value in the DS image is [8]:

where τ_n,(i,j) is the two-way traveling time, through the air and the wall, between the nth antenna and the ijth pixel location.

The conventional DS algorithm considers only a range of targets. This makes the radar scene contaminated. In order to obtain a clean radar scene and cross-range resolution that is independent of slant-range, the aperture segment length has to be directly proportional to the slant-range [9]. This is equivalent to keeping the integration angle at a fixed value. By using a radiation pattern window, a similar effect can be achieved simply. The DS algorithm can be rewritten as follows:

where w(n,(i,j)) is the radiation pattern window. The window matches the antenna's location and the ijth pixel to the radiation pattern. This formula makes the algorithm more close to real experimental scenario.

TCR is commonly used to evaluate the quality of a SAR image. TCR is calculated as [8]:

where A_t is the target area, A_c is the clutter area, and N_c is the number of pixels in the clutter area.

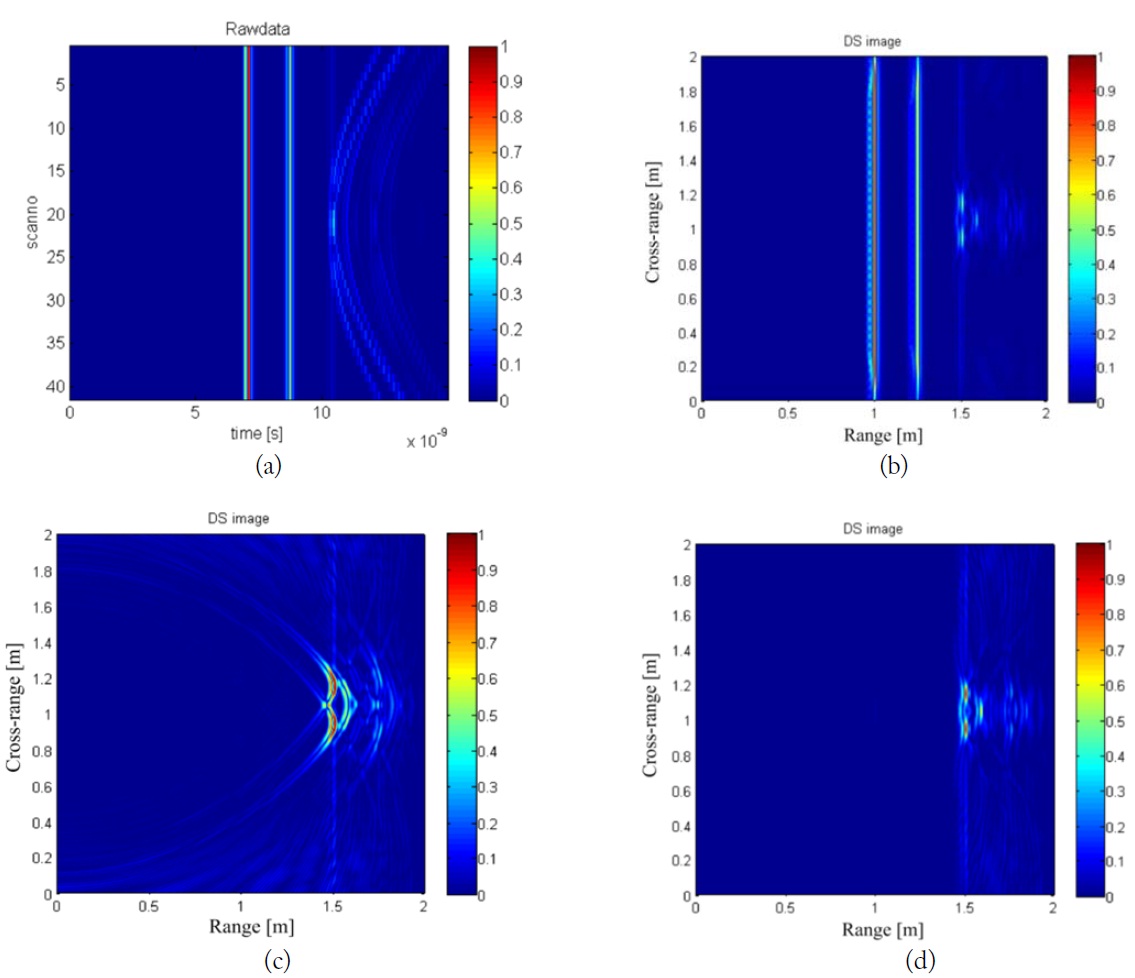
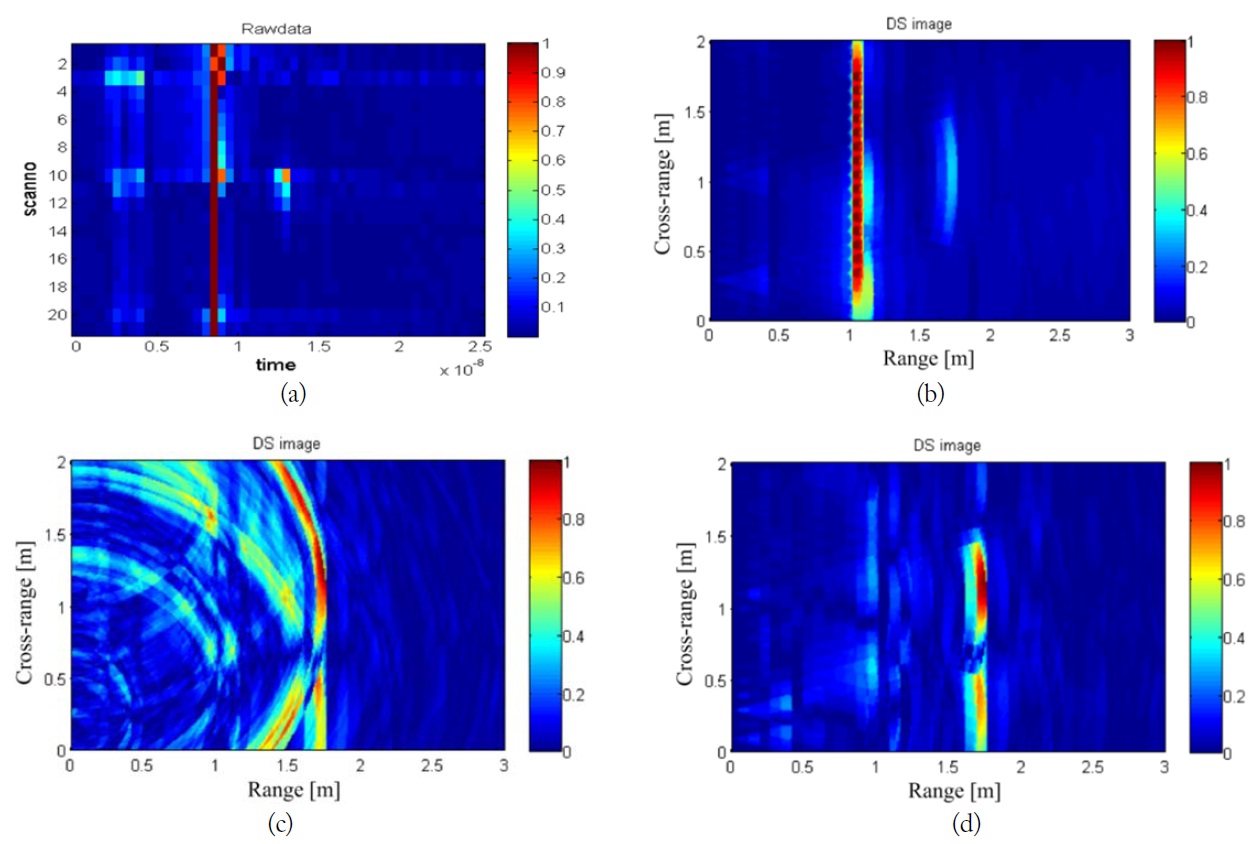
In order to verify the theory, we first consider the simulated data obtained through a finite-difference time-domain (FDTD) forward solver [10]. Elementary current sources located at a standoff distance of h_w = 1.25 m from the front face of the wall are employed and the field data are collected at N = 41 positions uniformly taken over the measurement line Ω = [0 2] m. The wall consists of a homogeneous dielectric layer of thickness d_w = 0.1 m, relative dielectric permittivity ԑ_w = 6.0, and conductivity σ = 0.02 (S/m) for the modeling of the concrete wall. A Ricker waveform with a center frequency f₀ = 2.5 GHz is used. As a simulation example, two circular metallic scatterers with a radius equal to 0.05 m are considered. The two circular scatterers’ centers are located at h_t = 0.3 m from the wall and separated with 0.2 m from the center of the Ω (See Fig. 2). Fig. 3 shows DS images of the scene reconstructed by two different DS algorithms. We assumed that the radiation pattern has cos¹⁰θ variation. The DS image is normalized to the maximum value of the image. The target-like signature and curvatures being shown along the horizontal line is the effect of interaction (multiple reflection) between the two targets. To remove them, additional signal processing techniques are needed. For quantitative evaluation of the quality of the images, Table 1 shows the TCR results of each DS algorithm.

Basically, the elementary current source has an isotropic radiation pattern so the pattern-based DS algorithm is not practical. However, using a directional radiation pattern window, we can reconstruct a more focused target image. In addition, assuming a directional pattern can make the wall clutter area cleaner. This makes the TCR superior to the conventional DS algorithm.

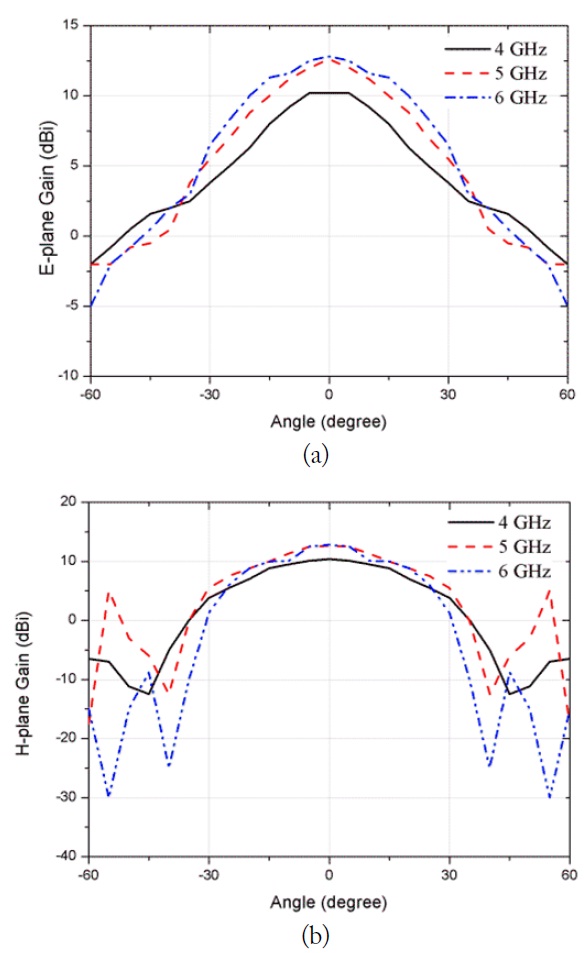
To validate the theory, an experiment is carried out. The experimental setup is implemented with dual-ridged horn antennas (DRH-020-180) [11] having radiation pattern of Fig. 4 and a vector network analyzer (VNA; Agilent E5071B). A linear array of 2.0 m and 0.1 m spacing between antenna locations is synthesized. The VNA generates a 2-GHz bandwidth stepped-frequency signal covering 4–6 GHz with a 40 MHz frequency step. Using an inverse Fourier transform (IFT), S₂₁ can be transformed from frequency domain data to time domain data [12]. The wall is placed at 1.0 m from the antenna and consists of a homogeneous plywood layer of thickness 0.02 m. The target is placed at 0.7 m from the wall and 0.1 m from the center of the measurement line (see Fig. 5).

Fig. 6 and Table 2 show the DS images and TCR results, respectively. To describe the radiation pattern more simply, we assumed that the radiation pattern has a cos¹⁰θ variation. This assumption fits well in a certain angle in which most of the energy exists. The TCR of the image reconstructed by the radiation pattern-based DS algorithm is improved 6.7 dB compared to the conventional DS algorithm. Some remaining clutter near the target in Fig. 6(c) is presumed to be the non-ideal  measurement effect. To mitigate that kind of error, more precise experiments are needed.

In this paper, the performance of the conventional and radiation pattern-based DS algorithms was presented. Synthetic and experimental data were used to evaluate the TCR. As a result, the TCR of the radiation pattern-based DS algorithm showed a remarkable improvement over the conventional DS algorithm.

There are two main reasons for this improvement. First, the radiation pattern-based DS algorithm prevents contamination of the radar scene with the same distance from the antenna to the target. Second, it concentrates the target signal more closely. In the simulation result, the target is imaged at a slightly longer distance from the antenna because we did not consider the wave delay in the dielectric medium. Future work could be directed toward the study of the effect of wall parameters in TWRI, wall clutter mitigation, TWRI in inhomogeneous wall cases, and so on.