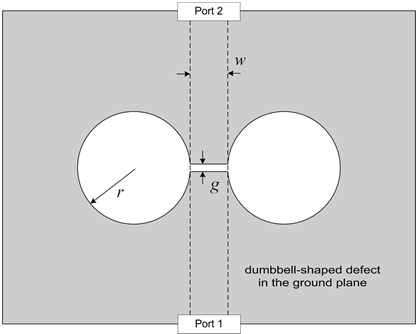
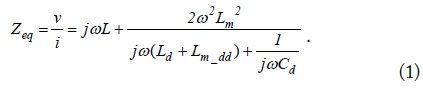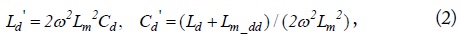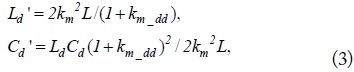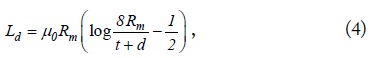A planar transmission line with a dumbbell-shaped defected ground structure (DGS) provides low-pass transmission characteristics with a wide rejection frequency band. Due to the wideband rejection property, DGSs with a dumbbell shape are popularly used in the suppression of undesired harmonics for microwave and millimeter wave circuits and in the design of low-pass filters [1,2]. To date, the analysis of the dumbbellshaped DGS loaded planar transmission lines has almost always involved utilizing commercial electromagnetic full-wave solvers. The simulated S-parameters are converted into the transmission (ABCD) and the impedance (Z) matrices and an equivalent LC resonator circuit model is derived from the matrices [1]. However, in those approaches, there is no direct correlation between the physical dimensions of the structure and the equivalent LC parameters. Furthermore, time-consuming iterative design procedures are required to accomplish the design goal.

In this paper, we propose a new equivalent circuit model for a dumbbell-shaped DGS coupled to a transmission line, especially a microstirp line, to provide design rule and physical insight. Also, simple approximate expressions are presented to determine the main circuit parameters for this model.

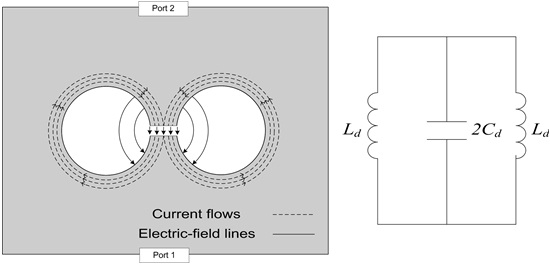
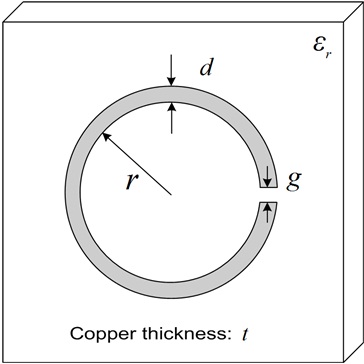
Fig. 1 illustrates the geometry of the microstrip line with a dumbbell-shaped DGS where two circular etched areas are connected by a narrow etched gap. In the DGS, the electric field is concentrated around the narrow etched gap while the current is confined to the metallic ground plane surrounding the circular etched pattern at resonance.

Hence the DGS in the ground plane can be represented by an LC resonant circuit model as shown in Fig. 2. Since there are two circular etched areas, two L_d are connected parallel to the capacitance of 2C_d in the resonant circuit for the DGS.

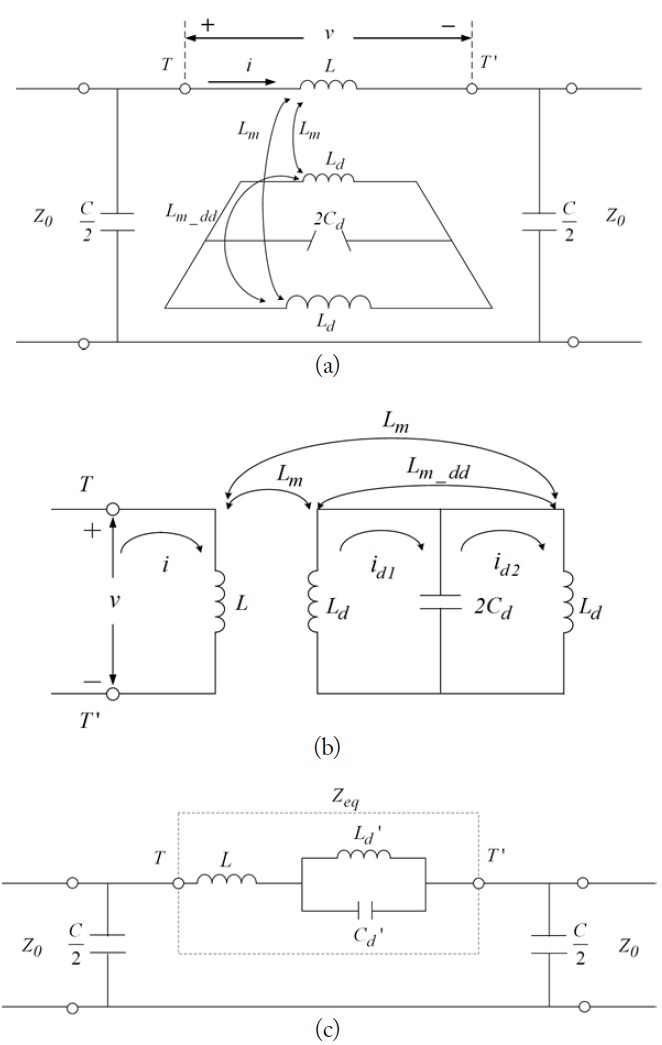
For the dumbbell-shaped DGS loaded microstrip line, the equivalent circuit model can be proposed as illustrated in Fig. 3(a). The magnetic flux from the current on the host transmitssion line passes through the wide etched circular area on the ground plane and it causes a magnetic coupling of the DGS to the host line. The L_m represents the mutual inductances coupling the DGS to the host line, and the L_{m_dd} is the mutual inductance between two L_d for etched circular areas. The L and  C are the inductance and capacitance of the microstrip transmission line corresponding to the length occupied by a unit cell of DGS, respectively.

To obtain a simplified equivalent circuit of the DGS, the equivalent impedance of the branch between T and T’ is analyzed by defining mesh currents as shown in Fig. 3(b), in which the mesh currents in the resonant circuit are the same (i_d1 = i_d2) due to the symmetry. Applying the voltage law around the meshes and solving for i and v, the equivalent impedance between T and T’, Z_eq is given by

From (1), the complex circuit between T and T’ can be replaced by a simplified equivalent circuit model as shown in Fig. 3(c). The expressions for the inductance and capacitance of the simplified equivalent circuit are given by

with the resonance angular frequency of At resonance, L_d’ and C_d’ are obtained in the simplified form

since L_m=k_m(LL_d)^1/2 and L_{m_dd}=k_{m_dd}L_d, where k_m is the magnetic coupling coefficient between the host transmission line and the resonator and k_{m_dd} is the magnetic coupling coefficient between two etched circular areas.

One of the aims in this paper is to find values of parameters of the equivalent circuit model for the dumbbell-shaped DGS coupled to the microstrip line. In the patterned ground plane, the current distribution is confined within the metallic periphery of the circular etched pattern, as shown in Fig. 2. Hence the inductance L_d for the left half of the dumbbell-shaped DGS can be calculated from the metallic split ring model seen in Fig. 4. As the etched gap is very narrow, the inductance of the split ring may be obtained from the formula for a ring as [3]

where R_m = r + d / 2 , t is the conductor thickness, and μ₀ is the free-space permeability.

In Fig. 2, the capacitance of the DGS on the ground plane consists of the gap capacitance and the surface capacitance. The gap capacitance is calculated by the expression for the parallelplate capacitor of the gap with the correction due to the fringing fields. The surface capacitance is calculated by the analytical expression for the surface capacitance of a metallic split ring [4].

By replacing the air and substrate regions of the microstrip by a homogeneous medium with an effective permittivity ε_e, the capacitance of the split ring for the narrow gap is

In (5) the first two terms are the expressions for the gap capacitance that accounts for the fringing effect [5], the third term is an analytical expression for the surface capacitance, and ε_e is the effective permittivity of the homogeneous medium with ε_e = ε₀ (ε_r +1) / 2 , where ε_r is the dielectric constant of the substrate.

In the DGS cell, since the inductance of the signal line is strongly coupled with the inductance of the split ring surrounding the etched area, the coupling coefficient k_m is assumed  to be a unity. It is also assumed that the k_{m_dd} is zero because the magnetic coupling between two split rings on the ground plane is negligible.

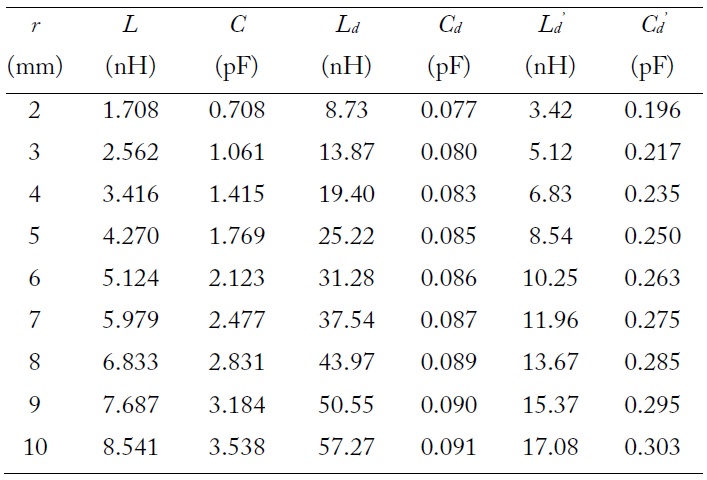
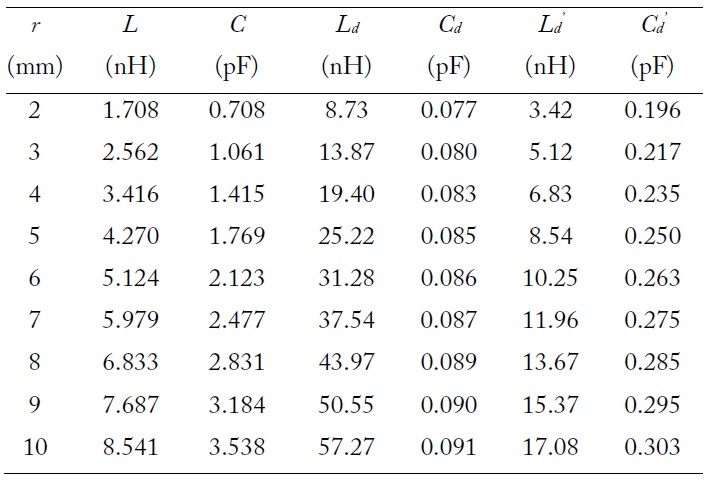
Having extracted circuit parameters using the analytic expressions in the previous section, L_d’ and C_d’ of the simplified equivalent circuit are calculated from (3). The circuit parameters are calculated for various radii of the etched circular pattern and the results are summarized in Table 1. In the design, a circuit board RO3010 with a dielectric constant of 10.2, copper thickness of 0.016 mm and substrate thickness of 1.27 mm is used. The characteristic impedance of the transmission line was designed to be 50 Ω (w = 1.2 mm) and the gap width of DGS was g = 0.4 mm. The width of the ring (d) is chosen here to be 0.6 mm. The width of 0.6 mm was chosen as this is the width that corresponds to the maximum concentration of the current distribution [6]. This optimum width changes slightly with an abrupt increase or decrease of the etched circular pattern radii, but 0.6 mm is a good approximation for which the computed results match with the simulated or measured ones.

The numerical calculations are performed for the simplified equivalent circuit model (Fig. 3(c)) with the extracted parameters in Table 1 by using the ADS, and the results are compared with the results from the electromagnetic (EM) simulation using the CST Microwave Studio.

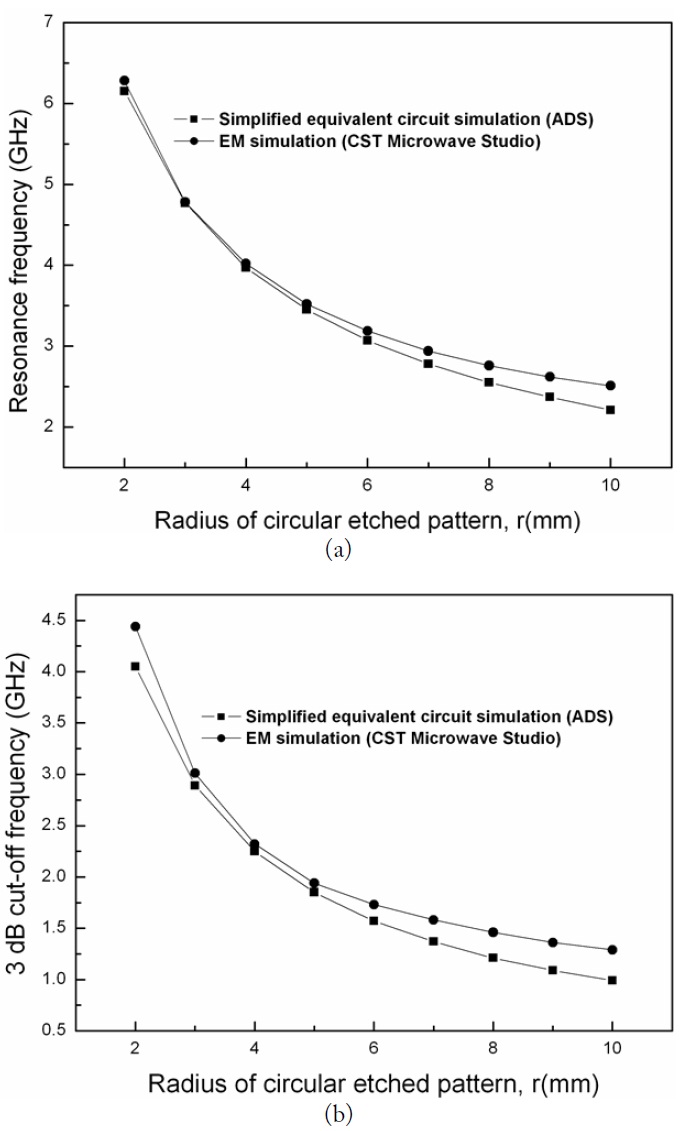
In Fig. 5, the resonance frequencies and 3dB cut-off frequencies calculated by the simplified circuit simulation and the EM simulation are plotted as functions of the radius of the etched circular pattern in the dumbbell-shaped DGS. The comparison between the results from the circuit modeling and the EM simulation shows that the proposed circuit model predicts the resonance frequencies and 3 dB cut-off frequencies with reasonable accuracy for a wide variation of radii from 2 to 10.

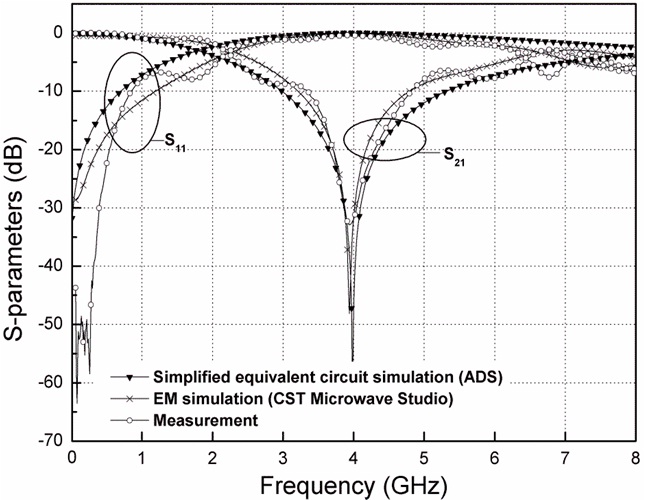
Fig. 6 illustrates the comparative transfer characteristics from the simulations and the measurement for a fabricated DGS with r = 4 mm. The resonance frequency and the stop bandwidth obtained from the measurements agree well with those from the circuit simulation and the EM simulation.

This paper has presented a new equivalent circuit model of a dumbbell-shaped DGS and simple approximate expressions to extract equivalent circuit parameters. The proposed equivalent circuit model provides an improved design method and physical insight into the electromagnetic behavior of the dumbbellshaped DGS.