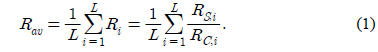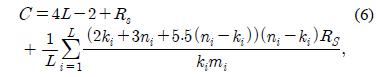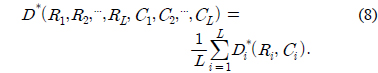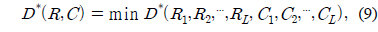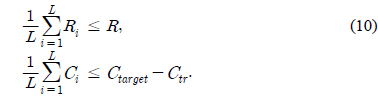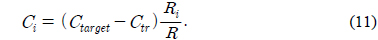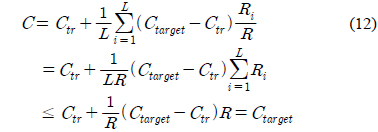일반적으로 Shannon의 소스-채널 코딩 분리 정리(source-channel coding separation theorem)[1]의 의거해서 통신시스템은 소스 코딩과 채널 코딩을 분리하여 각각 독립적으로 설계되어져 왔다[1-3]. 하지만, 이 정리는 무한한 길이의 블록 길이와 스테이션너리 소스에 한하여 적용된다. 따라서, 시스템의 복잡도와 지연에 제한이 있는 실제적인 시스템에 대해서 소스 코딩과 채널 코딩을 독립적으로 설계하여 순차적으로 연결한 탠덤 소스-채널 코딩(tandem source-channel coding) 시스템이 최적의 시스템이라 볼 수 없다.

실제적으로 시스템의 복잡도와 지연 제한이 있는 경우 탠덤 소스-채널 코딩 시스템보다 시스템 최종단의 왜곡을 줄이는 보다 효율적인 시스템을 얻고자 결합 소스-채널 코딩(joint source-channel coding) 시스템에 대한 많은 연구가 진행되어 왔다[3-12]. 이러한 결합 소스-채널 코딩의 우수성은 오류 지수(error exponent)에 대한 고찰에 의해 재차 확인되었다[9]. 결합 소스-채널 코딩의 한 예로 시스템의 복잡도가 낮은 상황에서 BPSK(binary phase shift keying) 변조 시스템에 대해 MAP(maximum a posterior) 경판정 복조에 바탕을 둔 COVQ(channel optimized vector quantization)의 설계를 들 수 있다[8]. 특별히 [10]에서는 시스템 복잡도와 지연의 제한 하에서 탠덤 소스-채널 코딩 시스템과 결합 소스-채널 코딩 시스템의 성능을 수치적으로 분석하여 제시하였다.

[10]에 의하면 주어진 시스템의 복잡도의 제한 하에서 탠덤 소스-채널 코딩 시스템과 결합 소스-채널 코딩 시스템 사이에 복잡도 문턱치가 존재한다는 것이다. 즉 주어진 시스템의 복잡도가 이 문턱치보다 클 때에는 탠덤 소스-채널 코딩 시스템의 성능이 우수하며, 주어진 시스템의 복잡도가 이 문턱치보다 작을 때에는 결합 소스-채널 코딩 시스템의 성능이 낫다는 것이다[10]. 본 논문에서는 균등 오류 보호 기법을 사용한 시스템에 대한 [10]의 분석을 보다 확장하여 비균등 오류 보호 기법을 사용한 탠덤 소소-채널 코딩 시스템의 복잡도에 따른 성능을 분석하고자 한다. 즉, 실제적으로 시스템 복잡도의 제한이 있는 시스템에서 비균등 오류 보호 기법을 적용한 탠덤 소스-채널 코딩 시스템과 결합 소스-채널 코딩 시스템의 성능을 수치적으로 제시하여 두 시스템의 복잡도에 따른 성능을 비교하고자 한다. 아울러 시스템 복잡도의 제한이 있는 상황에서 균등 오류 보호기법과 비균등 오류 부호 기법을 사용한 탠덤 소스-채널 코딩 시스템의 성능도 수치적으로 비교하고자 한다.

비균등 오류 보호 기법은 전달하고자 하는 정보, 일반적으로 소스 부호화된 비트의 중요도에 따라 채널 부호화를 달리 적용하는 기법을 말한다[13]. 특히 변환 부호화기가 사용된 시스템에서 각각의 변환 계수는 그 중요도가 달라 중요한 변환 계수는 보다 낮은 채널율의 채널 부호화를 사용하고 덜 중요한 변환 계수는 높은 채널율의 채널 부호화를 사용하여 잡음 채널을 통한 전송시 시스템 최종단의 왜곡을 최소화하자는 기법이다. 하지만, [13]에서는 Plyanskiy의 획득 범위를 만족하는 상당한 길이의 코드 길이가 사용된다면 비균등 오류 보호 기법이 균등 오류 보호 기법에 비해 얻는 성능 향상이 그리 크지 않음을 보였다. 코드 길이는 복잡도에 영향을 미치는 요소이므로 충분한 복잡도가 주어진 상황에서는 비균등 오류 보호 기법의 성능 이득이 낮다는 것이다. 본 논문에서는 이러한 문제에 수치적으로 접근하여 시스템의 복잡도에 따른 비균일 오류 보호 기법의 성능 향상에 대해서도 살펴 보고자 한다.

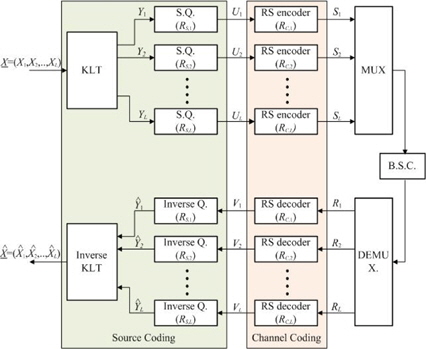
논문에서는 [10]에서 사용한 대표적인 탠덤 소스-채널 코딩 시스템과 결합 소스-채널 코딩 시스템을 사용하여 각각의 시스템에 대한 MSE(mean squared error)를 주어진 복잡도 하에서 최소화한다. 구체적으로 탠덤 소스-채널 코딩 시스템은 잡음이 없는 채널에 최적화된 전형적인 변환 부호화기와 RS(Reed-Solomon) 채널 부호화기로 구성되어 있으며, 결합 소스-채널 코딩 시스템은 Vaishampayan과 Farvardin[14]의 시스템을 사용한다. [10]에서와 마찬가지로 시스템의 복잡도를 부호화와 복호화에 필요한 산술 연산의 수로 표현하여 각 시스템에 대한 MSE를 Guass-Markov 소스에 대해 BSC(Binary Symmetric Channel)하에서 계산함으로써 복잡도에 따른 성능을 평가한다. 그 결과, 비균등 오류 보호의 탠덤 소스-채널 코딩 시스템의 복잡도 문턱값은 균등 오류보호의 탠덤 소스-채널 코딩 시스템의 문턱값보다 작아지며, 균등 오류 보호 시스템에 대한 비균등 오류 정정 기법의 시스템의 성능 향상은 시스템 복잡도가 높아질수록 작아짐을 확인하였다. 즉, [13]이 주장하는 바와 같이 시스템의 복잡도가 충분하게 주어진다면 비균등 소스-채널 부호 시스템의 성능 향상이 균등 소스-채널 부호 시스템에 비해 미약하다는 것을 수치적으로 확인할 수 있었다.

이 후 본 논문의 구성은 다음과 같다. 제 2장에서는 비교 분석하고자하는 시스템에 대해 설명하고 제 3장에서는 시스템의 왜곡과 복잡도를 분석한다. 이어 제 4장에서 최적화 및 결과에 대해 논하고 제 5장에서 결론을 맺는다.

본 논문에서 다루는 대표적인 시스템은 세 개의 시스템인데, 결합 소스-채널 코딩 시스템, 균등 오류 보호의 탠덤 소스-채널 코딩 시스템이외에 비균등 오류 보호의 탠덤 소스-채널 코딩 시스템이다. 이 중 균등 오류 보호의 탠덤 소스-채널 코딩 시스템과 결합 소스-채널 코딩 시스템은 [10]에서 분석한 시스템을 그대로 사용하였다. 여기서는, 비균등 오류 보호의 탠덤 소스-채널 코딩 시스템에 대해서 자세히 기술한다. 소스는 평균이 0이고 분산이 1이며 스테이션너리 Gauss-Markov 확률 변수를 사용하고 {X_i}로 표기한다. 그림 1은 L차원 변환소스 부호화기와 각각의 변환 계수를 다른 채널 코드율로 채널 코딩을 하는 L개의 RS(Reed-Solomon) 채널 코드로 구성된 비균등 오류 보호의 탠덤 소스-채널 코딩 시스템을 보여준다.

L개의 소스 샘플 X₁, X₂, ..., X_L은 L차원 KLT(Karhunen-Loeve Transform)에 의해 변환되고 각각의 변환계수 Y_i는 L개의 스칼라 양자화기에 의해 양자화된다. U_i는 양자화된 비트를 가리키며, 이는 i번째 RS 채널 부호화기로 입력되어 채널 코드워드 S_i가 된다. i번째 변환 계수의 소스 부호화율을 R_S,i, i번째 변환 계수에 대한 RS 채널 부호의 채널 부호화율을 R_C,i, i번째 변환계수에 할당된 비트수를 R_i,라 하면, 주어진 비트 할당, 즉 R₁, R₂, ..., R_L에서 평균 전송율 R_av는 다음과 같이 주어진다.

소스와 채널 부호화기를 거쳐 생성된 LR_av 개의 비트는 오류 확률이 p인 이진대칭채널(Binary Symmetry Channel; BSC)을 통해 전송된다. 전송된 비트는 RS 역부호화기, 역양자화기, 역변환 부호화기를 통해 복원되고 최종 복원된 데이터는 로 표기한다.

이 절에서는 비균등 오류 보호의 탠덤 소스-채널 코딩 시스템의 성능을 평가하기 위한 시스템 왜곡에 대해 기술한다. 본 논문에서는 시스템의 왜곡 평가 지표로 MSE(Mean Squared Error)를 사용하기로 한다. i번째 변환 계수 Y_i가 역양자화기 Q_i에 의해 복원되어 가 되므로 i번째 변환 계수에 대한 MSE는 아래의 식으로 주어진다.

전체 시스템에 대한 MSE는 다음의 식으로 표현된다.

여기서, D_i는 결합 소스-채널 코딩에서 널리 알려져 있듯이 소스 왜곡과 채널 왜곡의 합으로 표현된다[15].

여기서, D_S,i는 E[U_i − Q_i(U_i)]로 채널 오류가 없는 상황에서의 양자화에 의한 왜곡이고, D_C,i는 채널 왜곡으로써 채널 왜곡에 대한 자세한 표현은 [10]에 나타나 있다.

결합 소소 - 채널 코딩 시스템은 Vaishampayan과 Farvardin[14]의 채널 최적화 변환 부호화 시스템(Channel-Optimized Transform Coding System)을 사용하며 이에 대한 시스템 왜곡은 [14]의 방법을 사용하여 계산한다.

본 논문에서는 시스템의 복잡도의 측정 도구로 소스 샘플당 부호화와 복호화에 필요한 덧셈과 곱셈의 연산의 합을 사용한다. 탠덤 소스-채널 코딩 시스템과 결합소스-채널 코딩 시스템의 복잡도에 대한 분석은 [10]의 결과를 이용하는데, 채널 최적화 변환 부호화 시스템의 복잡도는 다음의 식으로 표현된다.

여기서, 로 평균 소스 부호화율이다. 비균일 오류 보호의 탠덤 소스-채널 코딩 시스템의 복잡도는 [10]의 균일 오류 보호 시스템의 결과를 이용하여, 소스 부호화인 식 (5)로 주어지는 변환 부호화기의 복잡도와 채널 부호화에 필요한 복잡도의 합으로 다음과 같이 주어진다.

여기서, i번째 RS 채널 코드는 (n_i,k_i,m_i)의 채널 코드이며, n_i는 채널 코드워드 길이, k_i는 정보 비트 길이, n_i = 2^m−1이며 R_C,i = k_i/n_i로 표현된다.

앞에서 기술된 시스템에 대해서 우리가 해야 할 과제는 주어진 제한 조건, 즉 전송률 R과 복잡도 C_target의 제한 하에서 식 (2)로 주어지는 MSE를 최소화하는 것이다. 제한 조건은 아래의 두 식으로 정리된다.

C_i를 i번째 양자화기와 RS 부호화기의 복잡도라고 하면, i번째 변환 계수의 왜곡 D_i는 R_i = R_S,i/R_C,i와 C_i의 함수가 된다. 식 (7)의 제한 조건을 만족하는 모든 스칼라 양자화기와 RS 채널 부호화기의 중에서 가장 작은 i번째 변환 계수의 왜곡값을 주는 스칼라 양자화기와 RS 채널 부호화기의 의한 왜곡값을 라 하자. 시스템은 L개의 부호화기로 이루어져 있으므로 각각의 변환 계수에 할당된 R₁, R₂, ..., R_L과 복잡도 C₁, C₂, ..., C_L의 조건 하에서 최소 전체 왜곡은 다음과 같이 주어진다.

이제, 전체 시스템의 왜곡을 최소화하기 위해서는 식 (7)의 제한 조건 하에서 최적의 비트 할당과 복잡도 할당을 해야 한다. 최적의 비트 할당과 복잡도 할당을 통해 얻어지는 전체 시스템의 최소 왜곡은 다음 식으로 표현된다.

여기서, 최소화하는 제약 조건은 아래와 같다.

변환 부호화기의 차원인 L 또한 정해져야 하는 파라 미터이다. 따라서, 우리의 최적화 문제는 전송률 R과 복잡도 C_target의 제한 하에서 전체 시스템의 왜곡을 최소하는 L, R₁, R₂, ..., R_L, 그리고 C₁, C₂, ..., C_L의 값을 찾는 문제로 귀결된다. 최적화는 먼저 L을 설정하고 설정된 L 에 대해 전송률 R과 복잡도 C_target을 L개의 변환 부호화기에 할당하는 과정으로 이루어진다. 즉, 변환부호화기 차원 L, 전송률 R, 복잡도 C_target 하에서 LR 전송 비트와 LC_target 연산을 L개의 자원으로 할당한다. 이러한 최적 할당을 선정된 여러 개의 L값에 대해 수행하고, 얻어진 각각의 최적치중에서 최소 왜곡을 주는 L, R₁, R₂, ..., R_L, C₁, C₂, ..., C_L 를 최종 최적값으로 선정한다.

최적의 할당을 찾는 문제는 매우 복잡한 문제가 되기 때문에, 본 논문에서는 전역 최적화 접근보다는 지역 최적화 방법을 사용하고자 한다. 즉, 다음의 식과 같이 복잡도를 전송률의 분배와 같은 분배율로 분배하기로 한다.

식 (11)의 복잡도 분배를 사용하면 식 (10)의 복잡도 제한 조건을 만족함을 쉽게 알 수 있다. 즉,

의 관계가 성립한다. 이렇게 전송률에 비례하는 복잡도 분배를 통해 최소의 왜곡을 얻을 수는 없겠지만, 전역 최적 성능을 보장하는 알고리즘이 현재까지 존재하지 않으며 개발하기가 쉽지 않기 때문에, 식 (11)과 같은 간단한 분배 방법을 사용하여 지역 최적 성능을 얻고자 한다. 최적의 전송률 배분은 전형적인 비트 할당 알고리즘을 통해 얻을 수 있다[16]. 우리가 수행한 최적화 과정에서 L값은 {1, 2, 4, 8, 16, 32, 64, 128}의 집합에서 선택하도록 하였다.

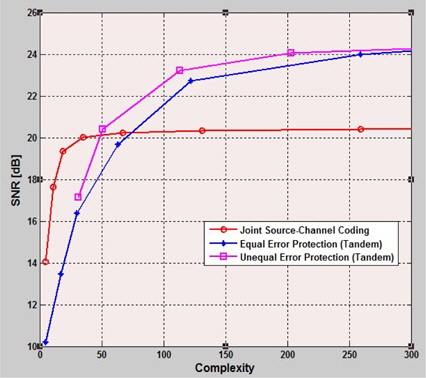
그림 2는 위와 같은 최적화 방법을 사용하여 얻은 시스템의 대표적인 성능을 보여 주고 있다. 여기서, R=5, p=0.01이며 복잡도 C_target에 따른 최적화된 균일 오류 보호의 탠덤 소스-채널 부호화 시스템, 채널 최적화된 변환 부호화 시스템, 그리고 비균일 오류 보호의 탠덤 소스-채널 부호화 시스템의 성능을 나타내었다. 그림에 보듯이, 성능은 SNR(Signal-to-noise ratio)로 측정하였는데, SNR은 10log₁₀(σ²/MSE)dB이다.

균일 오류 보호 시스템의 경우 결합 소스-채널 부호 시스템과의 복잡도 문턱값이 약 80이었으나, 비균일 오류 보호 시스템을 사용할 경우 그 복잡도 문턱값은 50의 낮아졌다. 즉 비균일 오류 보호 시스템은 탠덤 소스-채널 부호 시스템과 결합 소스-채널 부호 시스템 사이의 복잡도 문턱값을 낮춘다.

또한 균일 오류 보호 시스템에 대한 비균일 보호 시스템의 성능 향상은 모든 복잡도 제한에서 나타나는데, 복잡도 제한이 50에서 100사이에서 약 2 dB의 높은 성능 향상이 관찰되었다. 하지만, 복잡도의 제한값이 커지게 되면 될수록 그 성능 향상은 두드러지 않음을 볼 수 있다. 즉 충분한 정도의 복잡도의 제안 하에서는 비균일 오류 보호 시스템의 성능 향상은 매우 낮다고 볼 수 있다. 다시 말하면, 비균일 오류 보호 시스템은 복잡도의 제한이 심한 경우에 매우 효과적인 시스템이라고 볼 수 있다.

본 논문에서 복잡도의 제한이 있은 상황에서 탠덤 소스-채널 부호 시스템과 결합 소스-채널 부호 시스템의 성능을 비교 분석하였다. 특별히 탠덤 소소-채널 부호 시스템의 경우 기존의 연구에서 다루어졌던 균일 오류 보호 시스템을 확장하여 비균일 오류 보호 시스템을 주어진 복잡도의 제한 하에서 최적의 성능을 얻는 최적화를 수행하였다.

비균일 오류 보호 시스템을 사용하면, 기존에 알려진 탠덤과 결합 소스-채널 부호 시스템사이의 복잡도 문턱값을 낮추게 되며, 복잡도의 제한이 심한 상황에서 균일 오류 보호 시스템에 대한 성능 향상을 꾀할 수 있음을 알았다. 또한 충분한 복잡도가 주어진 경우에는 비균일 오류 보호 시스템의 균일 오류 보호 시스템에 대한 성능 향상이 거의 없음을 확인할 수 있었다. 따라서, 비균일 오류 보호의 탠덤 소스-채널 부호 시스템은 주어진 시스템의 복잡도 제한값이 낮은 경우에 효과적인 시스템이라고 할 수 있다.