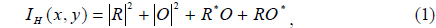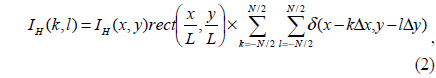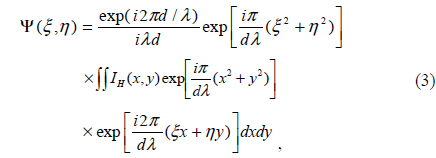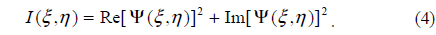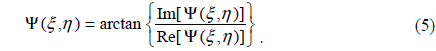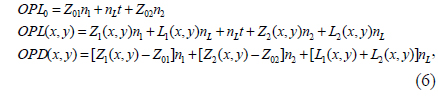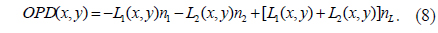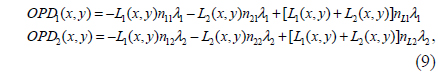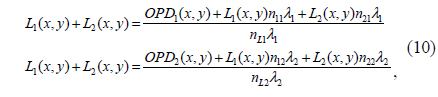Holography is a technique for recording phase modulation using interference patterns formed when light is reflected or transmitted by an object onto a photoplate. The recording requires object and reference beams, the combination of which generates the interference pattern. In the past, holographic interference patterns were recorded on film plates; presently, however, charge-coupled devices (CCDs) or complementary metal oxide semiconductor (CMOS) cameras are commonly used, and a computer reconstructs the hologram. Yaroslavskii et al. proposed a method for numerical hologram reconstruction in the 1970s, and Ounral and Scott used numerical reconstruction to measure the size of a particle, after improving on the reconstruction algorithm [1-6]. This method of digitally recording and reconstructing a numerical hologram is known as digital holography [7-10].

There are two types of digital holographic microscopes (DHMs): reflection and transmission. Typical optical components have two surfaces, front and back. However, transmission interferometers or DHMs cannot measure both three-dimensional (3D) surface profiles simultaneously, because the output from the optical components includes integrated surface information. In reflection interferometry, the phase information of each surface is measured separately and then numerically reconstructed to provide 3D information about the sample. Thus reflection interferometry is used to measure both 3D surface profiles. However, these approaches rely on movable mechanisms and accurate position determination to obtain all of the phase information. Low-coherence interferometry (LCI) could measure the surfaces by controlling the reference optical length as in optical coherence tomography, but LCI requires many images to obtain all of the phase information [11, 12].

In this paper we propose a method for simultaneously measuring the front and back surface profiles of transparent micro-optical components, using a dual-wavelength DHM [13-17] and liquids. We also propose a theoretical model for determining the surface information, and experimentally demonstrate the use of this model for an achromatic lens.

In the hologram recording process, a plane reference wave R and an object wave O interfere at the CCD. The hologram intensity is given by

where R* and O* denote the complex conjugates of the reference and object waves respectively [1, 2]. A digital holographic image can be recorded using a monochromatic CCD camera. The digital hologram I_H (k,l) is an N × N array resulting from two-dimensional sampling of IH (x,y) by the CCD camera, expressed as follows:

where k and l are integers, L × L denotes the area of the CCD chip, and Δx and Δy indicate the horizontal and vertical pixel sizes of the CCD.

If a screen is placed at a distance d behind the hologram, a real image is formed on the screen. Mathematically the amplitude and phase distributions in the plane of the real image can be calculated using the Fresnel-Kirchhoff integral [1, 2]. If a plane wave illuminates the hologram with an amplitude transmittance I_H (x,y), the Fresnel-Kirchhoff integral yields a complex amplitude Ψ(ξ,η) in the real image plane as

where λ is the wavelength and d is the reconstruction distance. From Eq. (3), the Fresnel-Kirchhoff integral can be considered as the Fourier transformation of the function I_H(x,y)exp[iπ(x² + y²)/λd] at the spatial frequencies ξ and η. Because Ψ(ξ,η) is an array of complex numbers, one can obtain an amplitude-contrast image using the intensity:

The quantitative phase image is obtained by calculating the argument [18-21]

The real 3D information is acquired by phase-unwrapping the quantitative phase image.

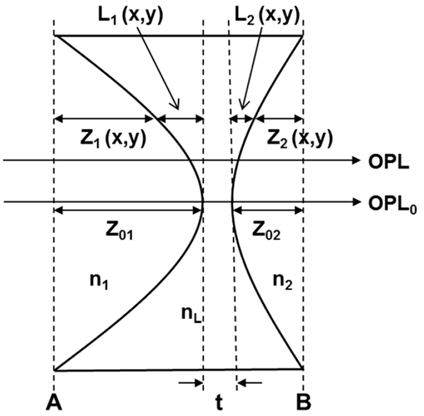
Consider the optical-path difference of a beam traveling through a transparent sample of refractive index n_L that is immersed in liquids with refractive indices n₁ and n₂ (see Fig. 1). The optical path length between planes A and B of the test surface can be described as [22]:

where Z_0i and Z_i (x,y) represent the vertex and surface height, respectively, and L_i (x,y) is the distance traveled from the surface to the vertex (i = 1, 2). OPD(x,y) is the path difference between OPL and OPL₀. The planes A and B are parallel, so the distance between them is constant. This determines the relationship between Z and L:

Substituting Eq. (7) into Eq. (6) gives

Equation (8) includes the integrated surface information [L₁(x,y) + L₂(x,y)] of the sample, not information about the individual surface profiles. Equation (8), therefore, represents the coupled information of the surface profiles and can be modified to include the effect of different wavelengths as follows:

OPD_i(x,y) (i = 1, 2) is the optical path difference at wavelength λ_i, while n_1i , n_2i and n_Li represent the refractive index of liquid and sample at wavelength λ_i, respectively. From Eq. (9) we find that the sets of information for individual surfaces, L₁(x,y) and L₂(x,y), are decoupled. The surface profile information in L₁(x,y) and L₂(x,y) can also be expressed as in Eq. (10):

The result above is obtained from the expression for the optical-path difference with two wavelengths and two different liquids. Equation (10) presents the decoupled surface profile information, and shows that both surface profiles of a transmission optical component can be measured simultaneously using a dual-wavelength DHM and two different liquids.

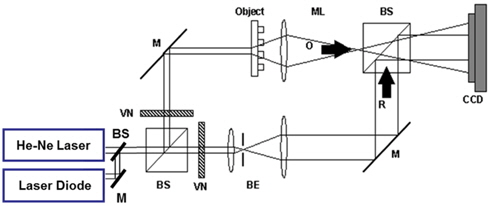
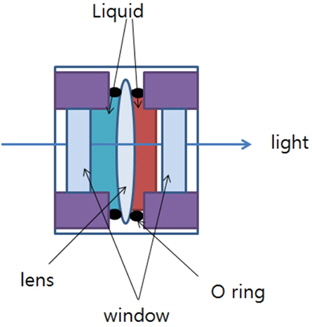
Figure 2 shows a schematic diagram of the experimental setup for a dual-wavelength transmission holographic microscope with liquids, for measuring both surfaces simultaneously. The basic experimental setup is similar to that of a Mach- Zehnder type interferometer. A 10-mW He-Ne laser (633 nm) and laser diode (532 nm) were used as the light sources. Water and a refractive index liquid (Cargille Laboratories) were used. The refractive index of the liquid was 1.6171 and 1.6317 at 633 and 532 nm, respectively, while that of water was 1.33168 and 1.33372 at 633 and 532 nm, respectively. Different liquids are filled as in Fig. 3.

We used a CCD camera (Imperx) to record the holograms. The pixel size and the number of pixels were 7.4 × 7.4 μm and 1024 × 1024, respectively. Achromatic lenses (Edmund Optics) were used as the samples, each with a different radius of curvature (ROC) 26.82 and 61.38 mm; and refractive indices of 1.51508 and 1.51947 at 633 and 532 nm, respectively.

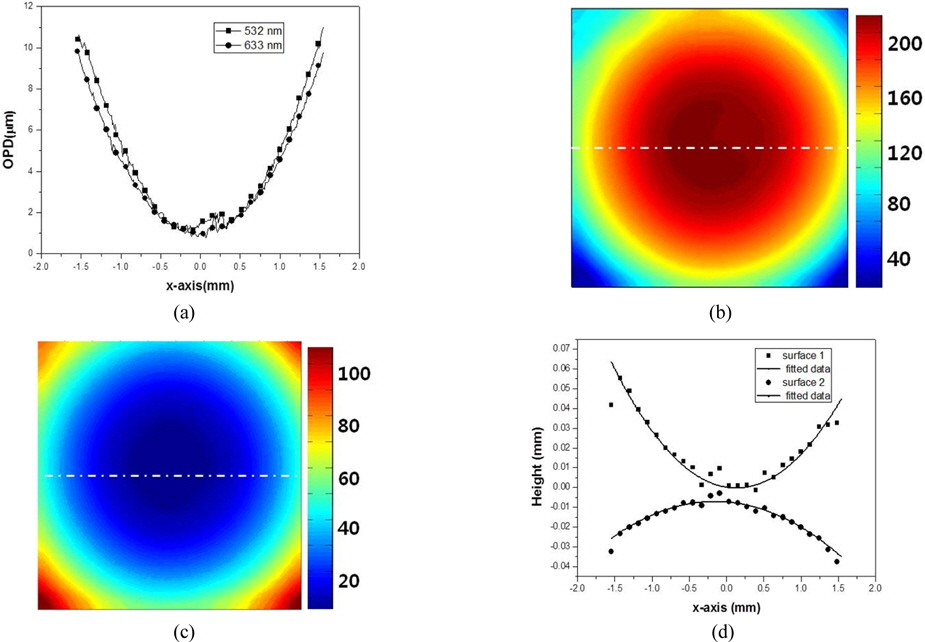
Figure 4 shows the experimental results for the achromatic lens from dual-wavelength DHM with liquids. Figures 4(a) and (b) show the holograms at 532 and 633 nm respectively. Figures 4(c) and (d) show respectively the reconstructed quantitative phase image of each hologram with 3D gray-level surface profiles of the samples shown in Figs. 4(e) and (f) for 532 and 633 nm. To acquire the 3D gray-level images, we used Flynn’s unwrapping method [23].

Figure 5(a) illustrates the gray levels measured along the dashed lines in Fig. 4(e) and Fig. 4(f). The squares and circles correspond to the results for wavelengths of 532 and 633 nm, respectively. The difference between the profiles for each wavelength was very small, as predicted by Eq. (9). The OPD includes information about the lens shape and refractive index; however, the OPD in Fig. 5(a) is not the actual height. The OPD difference between 532 and 633 nm is caused by the difference in the refractive indices. We calculated the front and back profiles using Eq. (10) and data from Figs. 4(e) and (f). The calculated results for the 3D color image from each surface are shown in Figs. 5(b) and (c). Note that the optical-path difference between the wavelengths, as well as noise, affected the calculated image. In Fig. 5(d) we show the spatial profiles indicated by the dashed lines in Figs. 5(b) and (c); the squares and circles correspond to the raw data, while the lines represent the fitted data. The fitted data show that the profile of each surface is different, and the surface information is decoupled. Next, we calculated the ROC from the calculated profiles. The ROC can be found from the completely reconstructed surface by fitting to a best-fit sphere using singular-value decomposition (SVD). Any spherical surface along the z-axis can be expressed as

where a and b are the coefficients of the curve. The ROC is given by . The calculated ROC values for the surfaces were 28.47 ± 1.22 and 60.54 ± 1.46 mm. These values were reasonably close to the design values, indicating that the proposed dual-wavelength DHM with liquids can be used for simultaneous measurement of the front and back profiles of a sample. Thus, unlike the many techniques available for measuring the surface profiles separately, the method described in this research provides the means to measure these profiles simultaneously. In this study we assume that the refractive indices of the studied materials are known; in future work we will investigate the case in which the refractive index of the sample is not known, or has a distribution.

Digital holographic microscopy can be used to measure optical-path differences with a high degree of accuracy. The optical-path difference depends on the refractive index and morphology of the samples. Normally optical components have a two-sided morphology, with front and back surfaces. We cannot determine the individual surface profiles with normal transmission DHM, because the output wave from the object presents integrated information. This study proposed a new experimental method and models for determining the individual surface profiles simultaneously using transmission DHM and liquids. We integrated dual-wavelength DHM with liquids and demonstrated a new method for determining the individual surface profiles of an achromatic lens, which has different ROC surfaces. The proposed method involves recording holograms at different wavelengths and then numerically reconstructing the phase information of the front and back 3D information of the sample. The proposed method can be applied to normal transmission interferometry for determining the 3D surface profiles of transmitted optical components.