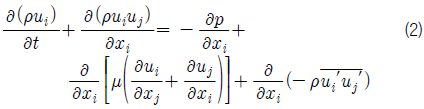The present study numerically investigated the effect of the advance ratio on the wake characteristics of the marine propeller in the propeller open water test. Therefore, a wide range of the advance ratio(0.2<J<0.8) and the region ranging from the trailing edge to one propeller diameter downstream location are considered to analyze the effect of advance ratio on the evolution of wake in terms of the tip vortices, slip stream and pressure. In order to simulate the incompressible viscous turbulent flow around the propeller, the Reynolds averaged Navier-Stokes (RANS) equations with the turbulence closure model of
‘선박제조연비지수(EEDI, energy efficiency design index)' 채택의 의무화는 그동안 지속적으로 연구되어져 왔던 친환경 고효율 추진기의 개발을 더욱 가속화 시키고 있다. 이러한 추진기 개발과 관련된 연구는 아래와 같이 크게 세 분야로 분류될 수 있다.
첫 번째, 프로펠러 단독 연구 (Lee, et al., 2004; Di Felice, et al., 2004; Felli, et al., 2006; Paik, et al., 2007; Felli, et al., 2011a), 두 번째로는 방향타 단독 연구 (Paik, et al., 2008a; Paik, et al., 2008b; Paik, et al., 2010; Wu & Liu 2011; Paik, et al., 2012)와 마지막으로 프로펠러와 방향타의 연계 연구(Van, et al., 2006; Felli, et al., 2011b)가 있다.
위에서 언급한 추진기에 관련된 다양한 연구들 중에서, 본 연구와 밀접한 관련이 있다고 판단되는 프로펠러 단독 연구들 은 다음과 같다. 먼저, 실험적 연구로서, Di Felice, et al. (2004)는 2차원 particle image velocimetry (PIV)를 사용하여 하중조건이 추진기 후류에 미치는 영향에 대한 연구를 수행하였다. 이를 위해, 서로 다른 세 가지 전진비(0.748, 0.88, 1.012)를 고려하였으며, 각 전진비에 대해 프로펠러 후류를 분석하였다. 이의 결과로서, 낮은 전진비에서 슬립스트림(slip stream)의 수축이 크게 나타나는 것을 보였으며, 또한, 전진비가 팁 및 허브 보텍스들의 거동에 영향을 미치는 것을 확인하였다.
Lee, et al. (2004)는 3차원 stereoscopic PIV(SPIV)를 사용하여 추진기 후류의 특성을 연구하였다. 따라서, 선행연구인 Di Felice, et al. (2004)의 2차원 PIV를 활용한 실험에서는 계측되어 질 수 없었던 프로펠러 회전방향 속도성분인 out-of-plane 속도를 포함한 추진기 후류의 3차원 유동장 특성을 보다 구체적으로 분석하였다. 이들도 Di Felice, et al. (2004)과 마찬가지로 하중조건이 추진기 후류에 미치는 영향에 분석하기 위하여 세가지 서로 다른 하중조건들(J=0.59, 0.72, 0.88)을 고려하였다. 이들은 하중조건이 증가할수록, 팁 보텍스의 강도와 스큐(skew)는 증가하며, 또한 out-of-plane 속도는 슬립스트림 내부에서 자유동속도 대비 8~13%정도 크기를 가지고 증가하는 것을 보였다.
Felli, et al. (2006)는 PIV와 slotting을 연동하여 프로펠러 후류의 속도장뿐만 아니라 이전 논문들에서 연구되어지지 않았던 속도장과 압력의 연관성에 관한 연구를 수행하였다. 팁 보텍스가 압력장 변화에 가장 지배적인 요소임을 제시하였다. 이러한 팁 보텍스가 유기하는 압력은 축(shaft)의 진동에 결과적으로 큰 영향을 미침을 확인하였다. 또한, 이 팁 보텍스는 먼 후류(far wake)에서 와의 분해(vortex breakdown) 과정동안 허브 보텍스의 변형을 강하게 유발함을 보였다.
위에서 언급한 PIV기반 실험적 연구들이 프로펠러 후류의 속도장 및 압력에 대해 연구를 주로 수행한 반면에, Paik, et al. (2007)은 PIV를 이용하여 프로펠러 팁 보텍스의 거동에 초점을 맞추었다. 이를 위해 보텍스 탐지법과 Galilean 분해법을 활용하여 보텍스의 가시화를 수행하였다. 두가지 방법 모두 팁 보텍스의 존재를 잘 증명하였으며, 보텍스 탐지법을 통해 도출한 팁 보텍스의 중심은 팁 보텍스의 궤적에 관한 자세한 정보를 제공하였다. 이러한 궤적을 통해, 보텍스가 일정 후류까지는 축을 향해 다가가다가, 이후, 더 이상 수축(contraction)되지 않고, 반경방향으로 진동하며 하류로 나아가는 것을 확인하였다.
Felli, et al. (2011a)은 LDV를 통하여 프로펠러 날개 수가 프로펠러 팁 보텍스에 미치는 영향을 연구하였다. 실험을 통해, 날개가 두 개인 프로펠러의 경우, 날개 끝에서 발생한 두 개의 보텍스가 하류로 나아가며 한 쌍의 보텍스로 합쳐지는 것을 확인하였다. 세 개인 경우는 한 쌍의 보텍스와 단일 보텍스로, 그리고 네개인 경우는 두 쌍의 보텍스가 하류로 나감을 보였다. 더 먼 영역(far wake)에서는 날개 수에 관계없이, 모든 팁 보텍스가 하나로 합쳐져 하류로 나아가는 것을 확인하였다. 팁 보텍스와 허브 보텍스는 프로펠러 후류의 불안정성에 지배적인 역할을 한다. 특히, 이중 팁 보텍스가, 전진비나 날개 수에 관계없이, 먼저 프로펠러 후류의 불안정성을 야기함을 발표하였다.
컴퓨터 기술이 발달함에 따라, CFD를 이용한 추진기 연구가 급격히 증가하고 있다. 하지만 현재까지 대부분 CFD를 이용한 프로펠러 단독 연구는, 유동의 특성보다는 프로펠러 해석에 도입된 수치해석 기법의 검증이나, 격자 및 난류모델의 의존성에 대한 연구(Morgut & Nobile, 2012; Peng, et al., 2013; Jang & Mahesh, 2013)가 주를 이루고 있다.
최근, Park, et al. (2011)은 CFD기반 추진기 후류 유동 특성에 관한 연구의 일환으로 전진비에 따른 프로펠러 후류의 총와도 수식모델링에 대한 연구를 수행하였다. 이를 위해, 폭 넓은 전진비(0.1~1)를 고려하였으며, 전진비가 클수록 총와도의 크기는 급격하게 감소하여 일정한 값으로 수렴함을 확인하였다. 이러한 전진비에 따른 프로펠러 후류에서의 총와도의 특성을 수치적으로 모델링하였다.
위에서 언급한 다양한 실험기반 연구들은 제한된 전진비에서 프로펠러의 후류가 포함하고 있는 다양한 유체역학적 특성들 중 주로 한가지 특성(와구조의 가시화, 압력, 팁 보텍스의 궤적 등)에 초점을 맞추어 연구를 수행하였다. 또한, 추진기 후류유동특성을 자세히 분석한 CFD기반 선행연구도 매우 드문 실정이다.
따라서, 본 연구는 폭 넓은 전진비(0.2~0.8)를 고려하여 전진비가 추진기 후류에 미치는 영향을 분석하였다. 특히, 선행연구에서 개별적으로 분석되어졌던 압력, 속도, 와도 등을 동시에 상세히 분석함으로써 추진기 후류의 유체역학적 특성을 보다 포괄적으로 제시하고자 하였다.
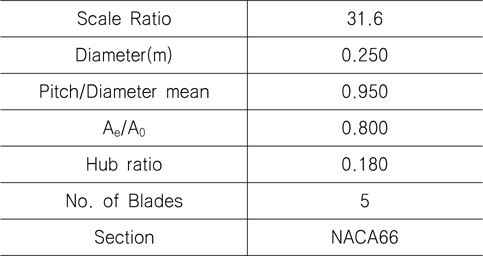
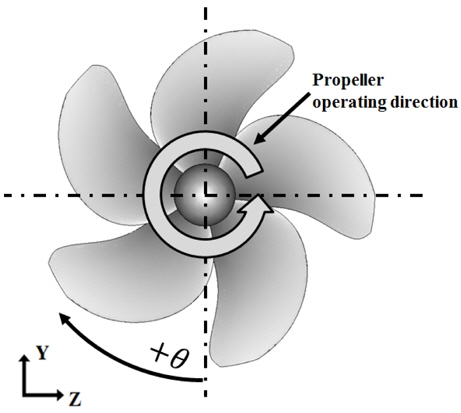
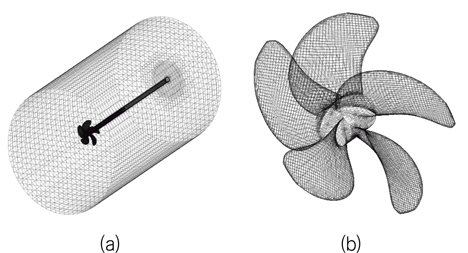
전진비가 추진기 후류에 미치는 영향을 연구하기 위해 본 연구에서 고려한 프로펠러는 한국해양과학기술원(KIOST)에서 설계한 3,600TEU컨테이너선(KRISO container ship, KCS)의 전용 프로펠러인 KP505이며, 그 제원은 Table1과 같다. 본 수치해석을 위해 도입된 좌표계는 Fig. 1과 같으며, 유속방향을 X축, 유속과 수직한 Y축과 Z축을 반경방향으로 선정하였다.
[Table 1] Principal particulars of KP505
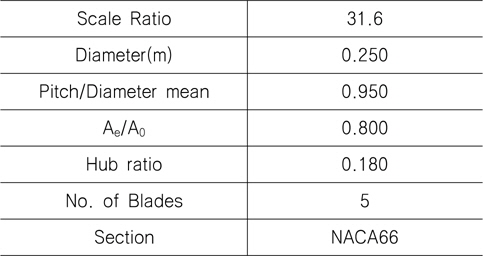
Principal particulars of KP505
본 연구에서는 범용 프로그램인 STAR CCM+를 사용하여 프로펠러 단독 시험 시험을 수치적으로 수행하였다. 비정상 비압축성 난류유동을 지배하는 방정식들로 아래의 연속방정식과 RANS(reynolds averaged navier-stokes) 방정식들이 고려되어졌으며, 아래의 식 (1)과 (2)에 각각 기술하였다.
여기서
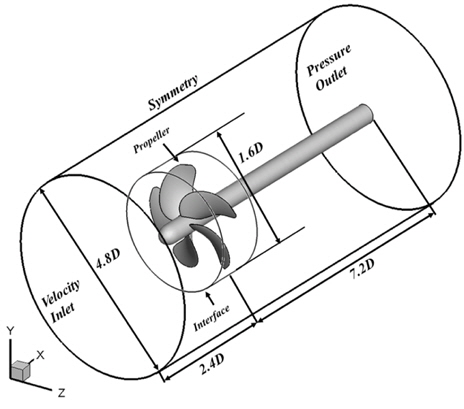
본 연구에서 고려한 계산영역과 경계조건을 Fig. 2에 도시하였다. 추진기 후류 유동을 모사하기 위하여 고려된 격자수는 약 250만개이며, 격자생성의 효율을 높이기 위해 도입한 다중블록(multi block)격자계를 사용하여 생성한 계산 전체영역에서 격자계 및 프로펠러 표면격자계를 Fig. 3에 나타내었다.
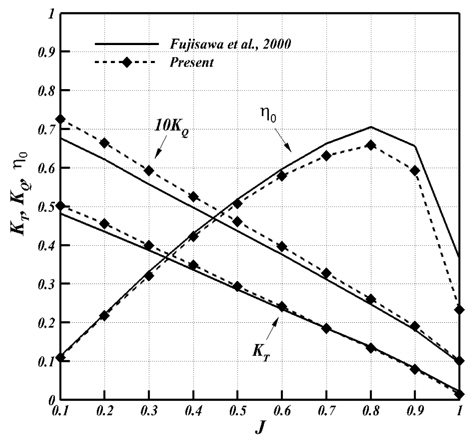
도입된 수치해석 기법의 검증을 위하여, 프로펠러 회전수는 12rps로 고정하였고, 입구유속을 변화시켜 전진비 0.1∼1.0 구간에서 0.1간격으로 총 10가지 경우를 고려하여 계산을 수행하였다.
추력계수(
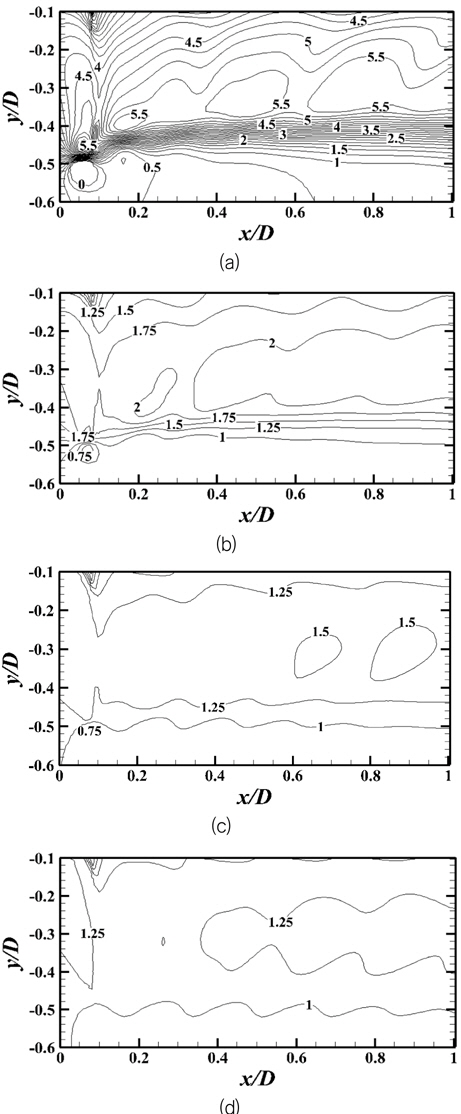
Fig. 5 는 위상각
프로펠러 후방에서 속도구배를 가지는 반류면은 슬립스트림 영역 안에 전진비에 관계없이 형성되어 임의의 간격을 가지며 하류로 나아가는 것을 Fig. 5에서 확인할 수 있다. 이는 프로펠러 후연과 날개끝에서 발생한 반류면이 연속적으로 발생했기 때문으로 보인다. 이러한 현상은 Lee, et al. (2004)이 실험으로 밝힌 현상과 유사한 형태를 갖는다
속도 구배는 전진계수가 작아질수록(하중이 증가될수록) 커지는 것을 확인 할 수 있다. Fig. 5에서는 각 영역의 속도 성분을 입구 유속으로 나누어 무차원화 된 속도(
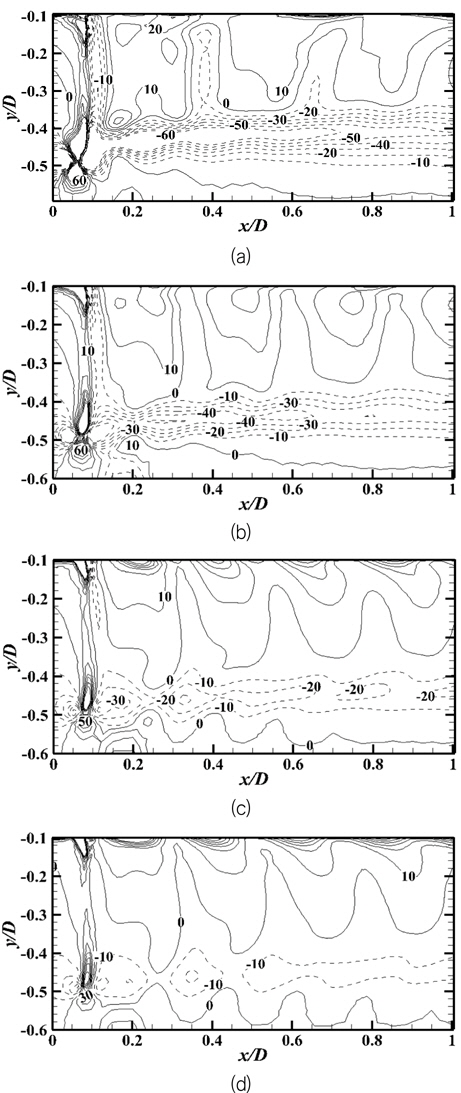
Fig. 6은 위상각
이러한 와의 상호작용은 이전 날개에서 발생한 팁 보텍스의 영향을 받아 후류에 나타나는 것으로 보인다. 이러한 영향으로 슬립스트림은 프로펠러축을 향해 수축/팽창이 반복되고, 하류로 나아감에 따라 슬립스트림의 수축/팽창은 점차 사라지는 것을 확인 할 수 있다.
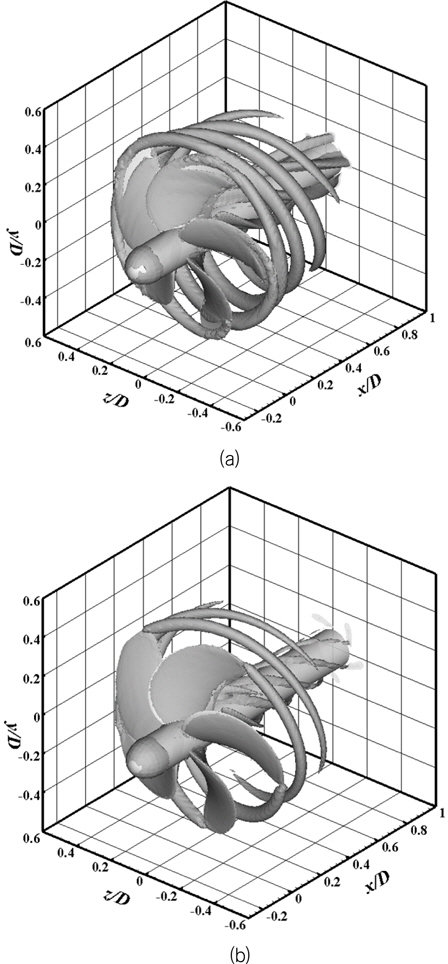
팁 보텍스의 궤적에 대한 정보는 프로펠러 설계에 있어서 매우 유용한 정보이다. 하지만 프로펠러 후류에 대한 와도장을 이용하여 보텍스의 중심을 찾아내는 작업은 소용돌이 운동이 없는 와도 지역을 포함하기에 적합한 방법이 아니다. 따라서, 본 연구에서는 후류 내에 존재하는 보텍스들의 정확한 위치를 탐지하기 위해 Zhou, et al. (1996)이 제안한 vortex identification method를 이용하였다. 이는 허수 고유치로부터 얻은 보텍스의 소용돌이 강도에 근거한 탐지 법으로, 소용돌이 운동이 전혀 없는 높은 와도 지역을 배제시켜 보텍스의 중심을 탐지하는 방법이다. Fig. 7은 두 전진비에서의 와 구조를 보여주는데 전진비가 낮을수록 크고 선명한 와가 생성되어 후류로 나아가는 것을 확인할 수 있으며, 높은 전진비에서는 이와 같은 현상이 현저히 줄어드는 것을 확인할 수 있다.
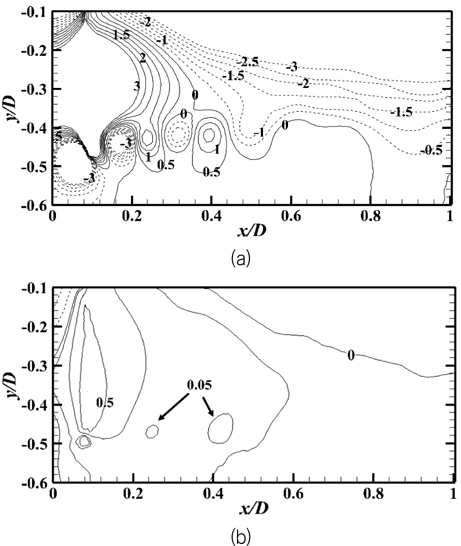
Fig. 8은 두 전진비에서의 압력장을 보여준다. 높은 하중 조건에서는 압력 면과 흡입 면을 따라 발생한 양/음의 압력이 서로 상호 작용을 하며 하류로 나아감과 동시에 축 부근에서는 높은 음 압력이 나타나는 것을 확인 할 수 있다. 하중 조건이 감소함에 따라 압력구배가 줄어들며 설계 전진비와 근접한 J=0.7에서는 높은 하중조건인 J=0.2와 비교하여 상대적으로 낮은 크기의 압력장이 나타난다.
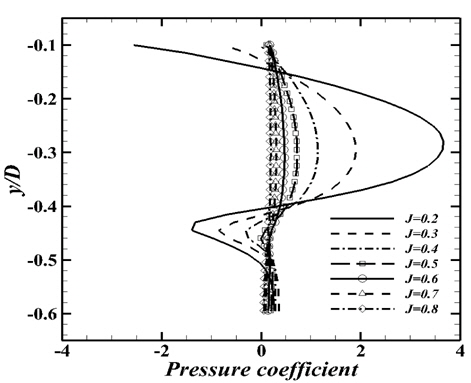
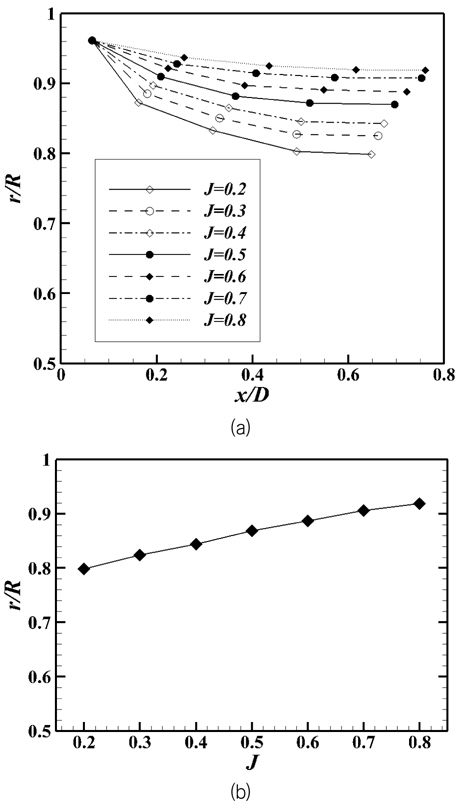
높은 하중조건에서 발생한 뚜렷한 압력구배는 하류로 나아가며 점점 약해지고, x/D=0.8을 지나면서 날개끝에서 발생한 압력 구배는 거의 사라지는 것을 확인할 수 있는데, 이는 Fig. 7에서 나타낸 와구조와 흡사한 경향을 갖는다. 또한 프로펠러 후연에서 발생한 양의 압력은 하류로 나아가며 그 성질이 줄어드는 것을 확인할 수 있다. 이러한 압력 구배는 프로펠러 근처(x/D=0.2)의 값을 나타낸 Fig. 9에서 명확히 확인 할 수 있다. 또한, 프로펠러 근방에서 발생한 양의 압력은 하중 증가에 따라 슬립스트림 내(−0.4 Fig. 10(a)는 모든 전진비에 대해 이전 날개에서 발생한 팁 보텍스의 중심점들을 연결하여 얻은 위치이다. 높은 하중조건에서는 슬립스트림의 강한 수축으로 인해 이전 날개에서 발생한 팁 보텍스의 수축 량이 더 큰 것을 확인 할 수 있으며, 이는 Fig. 10(b)를 통하여 좀 더 명확하게 확인 할 수 있다. 대표적으로 높은 하중조건 J=0.2와 낮은 하중조건인 J=0.8에서는 r/R이 약 0.8과 0.92에 해당하는 값으로 수축되는 것을 확인 할 수 있다. 이러한 현상은 앞서 분석한 속도와 압력을 포함한 여러 현상들의 상호작용에 의한 것으로 보인다.
본 연구는 CFD를 활용하여 전진비가 추진기 후류에 미치는 영향을 분석하였다. 도입된 수치해석기법들은 선행연구와 비교 및 검증을 통해 신뢰성을 확보하였다. 폭 넓은 전진비(0.2~0.8)를 고려하여, 전진비에 따른 후류의 특성들로서, 팁 보텍스의 거동, 슬립스트림 영역의 변형, 압력장과 팁 보텍스의 연계성 등을 자세히 분석하였다.
프로펠러 후연과 날개끝에서 연속적으로 발생하는 반류면은 전진비에 관계없이 형성되어지며 임의의 간격을 가지고 하류로 나아가는 선행 실험연구의 결과를 본 수치해석연구에서도 검증하였다. 전진비가 증가함에 따라 슬립스트림 영역 내의 상대속도가 감소함으로, 전단층이 약해지고 파형의 슬립스트림의 경계면이 형성됨을 확인하였다. 팁 보텍스와 압력은 낮은 전진비에서 보다 밀접한 상관관계를 보였다.