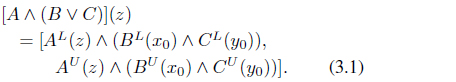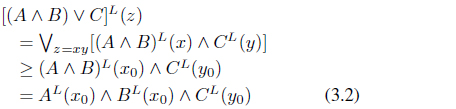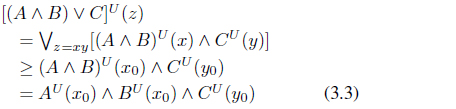In 1965, Zadeh [1] introduced the concept of a fuzzy set, and later generalized this to the notion of an interval-valued fuzzy set [2]. Since then, there has been tremendous interest in this subject because of the diverse range of applications, from engineering and computer science to social behavior studies. In particular, Gorzalczany [3] developed an inference method using interval-valued fuzzy sets.

In 1995, Biswas [4] studied interval-valued fuzzy subgroups. Subsequently, a number of researchers applied interval-valued fuzzy sets to algebra [5-11], and Lee et al. [12] furthered the investigation of interval-valued fuzzy subgroups in the sense of a lattice.

Later, in 1999, Mondal and Samanta [13] applied interval-valued fuzzy sets to topology, and Jun et al. [14] studied interval-valued fuzzy strong semi-openness and interval-valued fuzzy strong semicontinuity. Furthermore, Min [15-17] investigated interval-valued fuzzy almost M-continuity, the characterization of interval-valued fuzzy m-semicontinuity and intervalvalued fuzzy mβ-continuity, and then Min and Yoo [18] researched interval-valued fuzzy mα-continuity. In particular, Choi et al. [19] introduced the concept of an interval-valued smooth topology, and described some relevant properties.

In this paper, we discuss some interesting sublattices of the lattice of interval-valued fuzzy subgroups of a group.

In the main result of our paper, we consider the set of all interval-valued fuzzy normal subgroups with finite range that attain the same value at the identity element of the group. We prove that this set forms a modular sublattice of the lattice of interval-valued fuzzy subgroups. In fact, this is an interval-valued fuzzy version of a well-known result from classical lattice theory. Finally, we use a lattice diagram to exhibit the interrelationship among these sublattices.

In this section, we list some basic concepts and well-known results which are needed in the later sections. Throughout this paper, we will denote the unit interval [0, 1] as I. For any ordinary subset A on a set X, we will denote the characteristic function of A as χ_A.

Let D(I) be the set of all closed subintervals of the unit interval [0, 1]. The elements of D(I) are generally denoted by capital letters M,N, ···, and note that M = [M ^L,M ^U], where M ^L and M ^U are the lower and the upper end points respectively. Especially, we denote 0 = [0, 0], 1 = [1, 1], and a = [a, a] for every a (0, 1). We also note that (i) (∀M,N D(I)) (M = N M L= N L,M U = N U), (ii) (∀M,N D(I)) (M = N M L N L,M U N U). For every M D(I), the complement of M, denoted by M ^C, is defined by M ^C = 1 − M = [1 − M ^U, 1 − M ^L](See [13]).

Definition 2.1 [2,3]. A mapping A : X → D(I) is called an interval-valued fuzzy set (IVFS) in X, denoted by A = [A ^L,A ^U], if A ^L,A ^L I ^X such that A ^L A ^U, i.e., A ^L(x) A ^U(x) for each x X, where A ^L(x)[resp A ^U(x)] is called the lower[resp upper] end point of x to A. For any [a, b] D(I), the interval-valued fuzzy A in X defined by A(x) = [A ^L(x),A ^U(x)] = [a, b] for each x X is denoted by and if a = b, then the IVFS is denoted by simply . In particular, and denote the interval-valued fuzzy empty set and the interval-valued fuzzy whole set in X, respectively.

We will denote the set of all IVFSs in X as D(I) ^X. It is clear that set A = [A,A] ∈ D(I) ^X for each A ∈ I ^X.

Definition 2.2 [13]. Let A,B ∈ D(I) ^X and let {A_α}_α∈Γ ⊂ D(I) ^X. Then

(i) A ⊂ B iff A L ≤ B L and A U ≤ B U. (ii) A = B iff A ⊂ B and B ⊂ A. (iii) A C = [1 − A U, 1 − A L]. (iv) A ∪ B = [A L ∨ B L , A U ∨ B U].(iv)' Aα = [ ,]. (v) A ∩ B = [A L ∧ B L, A U ∧ B U]. (v)' Aα = [,].

Result 2.A[13, Theorem 1]. Let A, B, C ∈ D(I) ^X and let {A_α}_α∈Γ ⊂D(I) ^X. Then

(a) ⊂ A ⊂ . (b) A ∪ B = B ∪ A , A ∩ B = B ∩ A. (c) A∪(B∪C) = (A∪B)∪C , A∩(B∩C) = (A∩B)∩C. (d) A, B ⊂ A ∪ B , A ∩ B ⊂ A, B. (e) A ∩ ( Aα) = ( A ∩ Aα). (f) A ∪ ( Aα ) = (A ∪ Aα). (g) () c = , () c = . (h) (A c) c = A. (i) (Aα) c = A cα , ( Aα) c = Acα.

Definition 2.3 [8]. Let (X, ·) be a groupoid and let A D(I) ^X. Then A is called an interval-valued fuzzy subgroupoid (IVGP) in X if A L(xy) ≥ A L(x) ∧ A L(y) and A U(xy) ≥ A U(x) ∧ A U(y), ∀x, y X. It is clear that , IVGP(X).

Definition 2.4 [4]. Let A be an IVFs in a group G. Then A is called an interval-valued fuzzy subgroup (IVG) in G if it satisfies the conditions : For any x, y ∈G, (i) A L(xy) ≥ A L(x) ∧ A L(y) and A U(xy) ≥ A U(x) ∧ A U(y). (ii) A L(x −1) ≥ A L(x) and A U(x −1) ≥ A U(x). We will denote the set of all IVGs of G as IVG(G).

Result 2.A[8, Proposition 4.3]. Let G be a group and let {A_α} _α∈Γ ⊂ IVG(G). Then A_α ∈ IVG(G).

Result 2.B [4, Proposition 3.1]. Let A be an IVG in a group G. Then (a) A(x −1) = A(x), ∀x ∈ G. (b) A L(e) ≥ A L(x) and A U(e) ≥ A U(x), ∀x ∈G, where e is the identity of G.

Result 2.C [8, Proposition 4.2]. Let G be a group and let A ⊂ G. Then A is a subgroup of G if and only if [χ ^A, χ ^A] ∈ IVG(G).

Definition 2.5 [8]. Let A be an IVFS in a set X and let λ, μ ∈ I with λ ≤ μ. Then the set A ^[λ,μ] = {x ∈ X : A ^L(x) ≥ λ and A ^U(x) ≥ μ} is called a [λ, μ]-level subset of A.

In this section, we study the lattice structure of the set of intervalvalued fuzzy subgroups of a given group. From Definitions 2.1 and 2.2, we can see that for a set X, D(I)^X forms a complete lattice under the usual ordering of interval-valued fuzzy inclusion ⊂, where the inf and the sup are the intersection and the union of interval-valued fuzzy sets, respectively. To construct the lattice of interval-valued fuzzy subgroups, we define the inf of a family A_α of interval-valued fuzzy subgroups to be the intersection ⋂A_α. However, the sup is defined as the interval-valued fuzzy subgroup generated by the union ⋃ A_α and denoted by ( ⋃ A_α). Thus we have the following result.

Proposition 3.1. Let G be a group. Then IVG(G) forms a complete lattice under the usual ordering of interval-valued fuzzy set inclusion ⊂.

Proof. Let {A_α}_α be any subset of IVG(G). Then, by Result 2.A, ∈ IVG(G). Moreover, it is clear that A_α is the largest interval-valued fuzzy subgroup contained in A_α for each . So A_α = A_α. On the other hand, we can easily see that ( A_α) is the least intervalvalued fuzzy subgroup containing A_α for each . So A_α = ( A_α). Hence IVG(G) is a complete lattice.

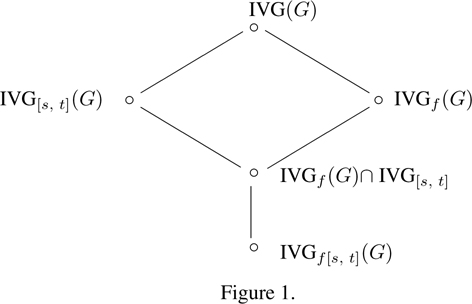
Next we construct certain sublattice of the lattice IVG(G). In fact, these sublattices reflect certain peculiarities of the intervalvalued fuzzy setting. For a group G, let IVG_f (G) = {A ∈ IVG(G) : Im A is finite } and let IVG_{[s, t]}(G) = {A ∈ IVG(G) : A(e) = [s, t]}, where e is the identity of G. Then it is clear that IVG_f (G)[resp. IVG_{[s, t]}(G)] is a sublattice of IVG(G). Moreover, IVG_f (G)∩ IVG_{[s, t]}(G) is also a sublattice of IVG(G).

Definition 3.2[11]. Let (X, ·) be a groupoid and let A,B ∈ D(I) ^X. Then the interval-valued fuzzy product of A and B, denoted by A B, is an IVFS in X defined as follows : For each x ∈ X, Now to obtain our main results, we start with following two lemmas.

Lemma 3.3. Let G be a group and let A,B ∈ IVG(G). Then for each [λ, μ] ∈ D(I), A ^{[λ, μ]} · B ^{[λ, μ]} ⊂ (A B) ^{[λ, μ]}.

Proof. Let z ∈ A^{[λ, μ]} · B^{[λ, μ]}. Then there exist x₀, y₀ ∈ G such that z = x₀y₀. Thus A^L(x₀) ≥ λ, A^U(x₀) ≥ μ and A^L(y₀) ≥ λ, A^U(y₀) ≥ μ. So and Thus . Hence

The following is the converse of Lemma 3.2.

Lemma 3.4. Let G be a group and let A, B ∈ IVG(G). If Im A and Im B are finite, then for each ,

Proof. Let Then and Since Im A and Im B are finite, there exist x₀, y₀ ∈ G with z = x₀y₀ such that and Thus A ^L(x₀) ≥ λ, A ^U(x₀) ≥ μ and B ^L(y₀) ≥ λ, B ^L(y₀) ≥ μ. So x₀ ∈ A ^{[λ, μ]} and y₀ ∈ B ^{[λ, μ]}, i.e., z = x₀y₀ ∈ A ^{[λ, μ]} · B ^{[λ, μ]}. Hence (A B) ^{[λ, μ]} ⊂ A ^{[λ, μ]} · B ^{[λ, μ]}. This completes the proof.

The following is the immediate result of Lemmas 3.3 and 3.4.

Proposition 3.5. Let G be a group and let A,B ∈ IVG(G). If Im A and Im B are finite, then for each [λ, μ] ∈ D(I), (A B) [λ, μ] = A [λ, μ] · B [λ, μ].

Definition 3.6 [8]. Let G be a group and let A ∈ IVG(G). Then A is called interval-valued fuzzy normal subgroup (IVNG) of G if A(xy) = A(yx) for any x, y ∈ G.

We will denote the set of all IVNGs of G as IFNG(G). It is clear that if G is abelian, then every IVG of G is an IVNG of G.

Result 3.A [6, Proposition 2.13]. Let G be a group, let A ∈ IFNG(G) and let such that λ ≤ A ^L(e) and μ ≤ A ^U(e). Then A ^{[λ, μ]} ◁ G, where A ^{[λ, μ]} ◁ G means that A ^{[λ, μ]} is a normal subgroup of G.

Result 3.B [6, Proposition 2.17]. Let G be a group and let A ∈ IVG(G). If A ^{[λ, μ]} ◁G for each [λ, μ] ∈ Im A, Then A ∈ IVNG(G).

The following is the immediate result of Results 3.A and 3.B.

Theorem 3.7. Let G be a group and let A ∈ IVG(G). Then A ∈ IVNG(G) if and only if for each [λ, μ] ∈ Im A, A ^{[λ, μ]} ◁ G.

Result 3.C[8, Proposition 5.3]. Let G be a group and let A ∈ IVNG(G). If B ∈ IVG(G), then B A ∈IVG(G).

The following is the immediate result of Result 2.A and Definition 3.6.

Proposition 3.8. Let G be a group and let A, B ∈ IVNG(G). Then A ∩ B ∈ IVNG(G).

It is well-known that the set of all normal subgroups of a group forms a sublattice of the lattice of its subgroups. As an interval-valued fuzzy analog of this classical result we obtain the following result.

Theorem 3.9. Let G be a group and let IVN_{f[s, t]}(G) = {A ∈ IVNG(G) : Im A is finite and A(e) = [s, t]}. Then IVN_{f[s, t]}(G) is a sublattice of IVG_f (G)∩ IVG_{[s, t]}(G). Hence IVN_{f[s, t]}(G) is a sublattice of IVG(G).

Proof. Let A, B ∈ IVN_{f[s, t]}(G). Then, by Result 3.C, AB ∈ IVG(G). Let z ∈ G. Then [Since A(e) = (s, t) = B(e)] = A L(z). [By Result 2.B] Similarly, we have (A B) ^U(z) ≥ A ^U(z). Thus A ⊂ A B. By the similar arguments, we have B ⊂ A B.

Let C ∈ IVG(G) such that A ⊂ C and B⊂ C. Let z ∈ G. Then Similarly, we haveThus A B ⊂ C. So A B = A ∨ B.

Now let [λ, μ] ∈ D(I). Since A,B ∈ IVNG(G), A ^{[λ, μ]}◁G and B ^{[λ, μ]}◁G. Then A ^(λ,μ) B ^{[λ, μ]}◁G. By Proposition 3.5, (A B) ^{[λ, μ]} ◁ G. Thus, by Theorem 3.7, A B ∈ IVNG(G). So A ∨ B ∈ IVN_{f[s, t]}(G). From Proposition 3.8, it is clear that A ∧ B ∈ IVNG(G). Thus A ∧ B ∈ IVN_f[s,t](G). Hence IVN_f[s,t](G) is a sublattice of IVG_f∩ IVG_[s,t](G), and therefore of IVG(G). This complete the proof.

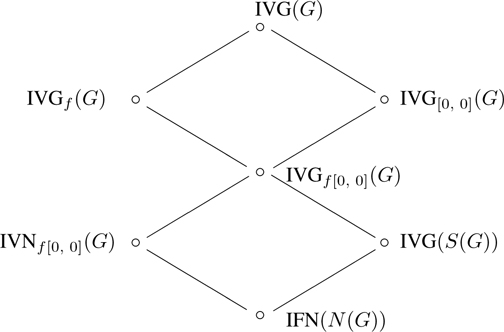
The relationship of different sublattice of the lattice of interval-valued fuzzy subgroup discussed herein can be visualized by the lattice diagram in Figure 1.

It is also well-known[20, Theorem I.11] that the sublattice of normal subgroups of a group is modular. As an interval-valued fuzzy version to the classical theoretic result, we prove that IVN(_{[s, t]}(G) forms a modular lattice.

Result 3.D [11, Lemma 3.2]. Let G be a group and let A ∈ IVG(G). If for any x, y ∈ G, A ^L(x) < A ^L(y) and A ^U(x) < A ^U(y), then A(xy) = A(x) = A(yx).

Definition 3.10 [20,21]. A lattice (L,∧,∨) is said to be modular if for any x, y, z ∈ L with x ≤ z[resp. x ≥ z], x∨(y∧z) = (x ∨ y) ∧ z[resp. x ∧ (y ∨ z) = (x ∧ y) ∨ z].

In any lattice L, it is well-known [21, Lemma I.4.9] that for any x, y, z ∈ L if x ≤ z[resp. x ≥ z], then x ∨ (y ∧ z) ≤ (x ∨ y) ∧ z[resp. x ∧ (y ∨ z) ≥ (x ∧ y) ∨ z]. The inequality is called the modular inequality.

Theorem 3.11. The lattice IVN _{f[s, t]}(G) is modular.

Proof. Let A,B,C ∈ IVN_{f[s, t]}(G) such that A ⊃ C. Then, by the modular inequality, (A∧B)∨C ⊂ A∧(B∨C). Assume that A ∧ (B ∨ C) ⊄ (A ∧ B) ∨ C, i.e., there exists z ∈ G such that [A ∧ (B ∨ C)] L(z) > [(A ∧ B) ∨ C] L(z) and [A ∧ (B ∨ C)] U(z) > [(A ∧ B) ∨ C] U(z). Since Im B and Im C are finite, there exist x₀, y₀ ∈ G with z = x₀y₀ such that (B ∨ C)(z) = (B C)(z) (By the process of the proof of Theorem 3.9) Thus

On the other hand,

and

By (3.1), (3.2) and (3.3),

A ^L(z) ∧ B ^L(x₀) ∧ C ^L(y₀) > A ^L(x₀) ∧ B ^L(x₀) ∧ C ^L(y₀)

and

A ^U(z)∧B ^U(x₀)∧C ^U(y₀) > A ^U(x₀)∧B ^U(x₀)∧C ^U(y₀).

Then

A ^L(z),B ^L(x₀),C ^L(y₀) > A ^L(x₀) ∧ B ^L(x₀) ∧ C ^L(y₀)

and

A ^U(z),B ^U(x₀),C ^U(y₀) > A ^U(x₀) ∧ B ^U(x₀) ∧ C^U(y₀).

Thus

A ^L(x₀) ∧ B ^L(x₀))∧ C ^L(y₀) = A ^L(x₀)

and

A ^U(x₀) ∧ B ^U(x₀) ∧ C ^U(y₀) = A ^U(x₀).

So

A ^L(z) > A ^L(x₀), A ^U(z) > A ^U(x₀)

and

C ^L(y₀) > A ^L(x₀), C ^U(y₀) > A ^U(x₀).

By Result 2.B,

A ^L(x₀ ⁻¹) = A ^L(x₀) < A ^L(x₀y₀)

and

A ^U(x₀ ⁻¹) = A ^U(x₀) < A ^U(x₀y₀).

By Result 3.D, A(x₀) = A(x₀ ⁻¹x₀y₀) = A(y₀).

Thus

C ^L(y₀) > A ^L(y₀) and C ^U(y₀) > A ^U(y₀).

This contradicts the fact that A ⊃ C. So A ∧ (B ∨ C) ⊂ (A ∧ B) ∨ C. Hence A ∧ (B ∨ C) = (A ∧ B) ∨ C. Therefore IVN_f[s,t](G) is modular. This completes the proof.

We discuss some interesting facts concerning a special class of interval-valued fuzzy subgroups that attain the value [1, 1] at the identity element of G.

Lemma 3.12. Let A be a subset of a group G. Then where < A > is the subgroup generated by A.

Proof. Let 𝐵 = {B ∈ IVG(G) : [χ_A, χ_A] ⊂ B}, let B ∈ 𝐵 and let x ∈ A. Then χA(x) = 1 ≤ BL(x) and χA(x) = 1 ≤ BU(x). Thus B(x) = [1, 1]. Since B ∈ IVG(G), B = for any composite of elements of A. So [χ, χ] ⊂ B. Hence [χ, χ>] ⊂ ⋂ 𝐵. By Result 2.C, [χ, χ] ∈ IVG(G). Moreover, [χ, χ] ∈ 𝐵. Therefore [χ, χ] = ⋂ 𝐵 =< [χ, χ] >.

The following can be easily seen.

Lemma 3.13. Let A and B subgroups of a group G. Then (a) A ◁ G if and only if [χA, χA] ∈IVN(G). (b) [χA,χA] [χB, χB] = [χA·B, χA·B].

Proposition 3.14. Let S(G) be the set of all subgroup of a group G and let IVG(S(G)) = {[χ_A, χ_A] : A ∈ S(G)}. Then IVG(S(G)) forms a sublattice of IVG_f (G) ∩ IVG_[1,1](G) and hence of IVG(G).

Proof. Let A,B ∈ S(G). Then it is clear that [χ_A, χ_A] ∩ [χ_B, χ_B] = [χ_A∩B, χ_A∩B] ∈ IVG(S(G)). By Lemma 3.12,

< [χ_A, χ_A] ∪ [χ_B, χ_B] > = < [χ_A∪B, χ_A∪B] > = [χ_<A∪B>, χ_<A∪B>].

Thus

[χ_A, χ_A]∨[χ_B, χ_B] =< [χ_A, χ_A]∪[χ_B, χ_B] >∈ IVG(S(G)).

Moreover, IVG(S(G)) ⊂ IVG_f (G)∩ IVG_[1,1](G).

Hence IVG(S(G)) is a sublattice of IVG_f (G)∩IVG_[1,1](G).

Proposition 3.14 allows us to consider the lattice of subgroups S(G) of G a group G as a sublattice of the lattice of all intervalvalued fuzzy subgroups IVG(G) of G.

Now, in view of Theorems 3.9 and 3.11, for each fixed [s, t] ∈ D(I) , IVN_{f[s, t]}(G) forms a modular sublattice of IVG_f(G)∩ IVG_{[s, t]}(G). Therefore, for [s, t] = [1, 1], the sublattice IVN_{f[1, 1]}(G) is also modular. It is clear that IVNf[1, 1](G) ∩ IVG(S(G)) = IVN(N(G)); where N(G) denotes the set of all normal subgroups of G and IVN(N(G)) = {[χ_N, χ_N] : N ∈ N(G)}. Moreover, IVG(N(G)) is also modular.

The lattice structure of these sublattices can be visualized by the diagram in Figure 2,

By using Lemmas 3.12 and 3.13, we obtain a well-known classical result.

Corollary 3.15. Let G be a group. Then N(G) forms a modular sublattice of S(G).

Lee et al. [11] studied interval-valued fuzzy subgroup in the sense of a lattice. Cheong and Hur [5], Lee et al. [10], Jang et al. [6], Kang and Hur [8] investigated interval-valued fuzzy ideals/(generalized) bi-ideals, subgroup and ring, respectively.

In this paper, we mainly study sublattices of the lattice of interval-valued fuzzy subgroups of a group. In particular, we prove that the lattice IVN_{f[s, t]}(G) is modular lattice (See Theorem 3.11). Finally, for subgroup S(G) of a group G, IVG(S(G)) forms a sublattice of IVG_f (G)∩ IVG_[1,1](G) and hence of IVG(G) (See Proposition 3.14).

In the future, we will investigate sublattices of the lattice of interval-valued fuzzy subrings of a ring.