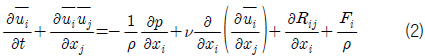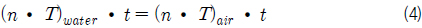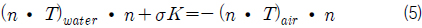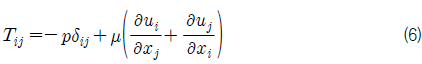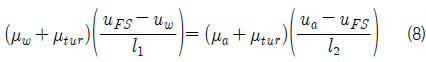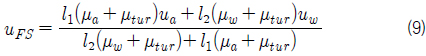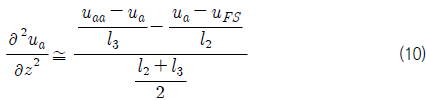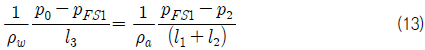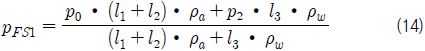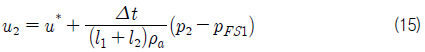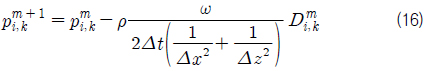Numerical simulations for the flows containing free surface remain difficult problems because the drastic differences of physical properties of water and air, The difference of densities makes the solution instable in particular. For the stabilities of the solutions, the most typical methods to simulate free surface flows, such as Volume Of Fluid(VOF) and Level-Set(LS) methods, impose transient zones where the physical prosperities are continuously distributed. The thickness of the transient zone is the source of the numerical errors. The other side, marker-density method does not use such a transient zone. In the traditional marker-density method, however, the air velocities of free surface cells are extrapolated from the water velocity, and the pressures on the free surface are extrapolated from the air pressures for the stability of the solution. In this study, the marker-density method is modified for the decrease of such numerical errors. That is, the pressure on the free surface is determined to coincide with the pressure gradient terms of the governing equations, and the velocity of free surface cells are calculated with the governing equations. Two-dimensional steady spilling breakers behind of a submersed hydrofoil and three-dimensional spilling breaker near a wedge shaped ship model are simulated using INHAWAVE-II including the modified marker-density(MMD) method. The results are compared with the results of Fluent V6.3 including VOF method and several published research results.
선박 및 해양구조물의 유체역학적 성능을 평가하거나, 그것들을 설계하기 위해서는 자유수면을 포함하는 유동을 해석하는 것이 필수적이다. 그러나 물과 공기의 큰 밀도와 점성계수의 차이로 인하여 자유수면을 수치적으로 해석하는 것은 아직까지 그리 쉽지 않은 문제로 남아있다. 이러한 유체영역 사이에 물리적 값들의 차이(공간적 불연속성)로 인하여 발생하는 해의 불안정성을 해결 또는 회피하기 위한 가장 일반적인 방법이 유체의 성질이 연속적으로 변하는 가상의 천이영역을 설정하는 방법이다. 현재 공학적으로 가장 널리 사용되고 있는 Volume of Fluids(VOF)법 (Hirt & Nichols, 1981)은 체적함수의 수송방정식을 계산하여 얻은 체적함수를 이용하여 자유수면의 위치를 결정하고 체적함수를 이용하여 물과 공기의 밀도와 점성계수를 가중평균 하여 지배방정식의 밀도와 점성계수로 사용하는 방법이다. VOF법은 많은 공학적 문제에 유용한 결과를 주지만 격렬한 유동이 지속되면, 체적함수가 넓게 퍼지게 되어 천이영역이 너무 넓어져 해의 정도가 떨어지는 문제를 가지고 있다. 체적함수가 넓게 퍼지는 것은 수송방정식이 대류방정식으로서 수치적으로 확산되기 때문이다. 그렇기 때문에 VOF법의 정도를 향상시키기 위한 연구들은 이러한 수치확산을 감소시키기 위한 방법이 주로 연구되어 왔다 (Zhao & Hu, 2011; Hu & Kashiwagi, 2004; Yu & Chen, 2009; Lopez, et al., 2005).
VOF법 이외에 공학적으로 많이 활용되는 또 다른 방법으로 Level-Set(LS)법 (Osher & Sethian, 1988)이 있다. LS법은 VOF법에서 체적함수가 넓게 퍼지는 문제를 없애기 위해서 고안된 방법으로 격자점과 자유수면 사이의 거리(거리함수, level-set function)를 이용하여 지배방정식의 밀도와 점성계수를 결정하는 방법이다. 거리함수도 대류방정식으로서 수치적인 확산이 발생하게 되고, 이러한 문제를 해결하기 위하여 정해진 시간단계마다 거리함수를 재초기화 한다. 이러한 재초기화 과정에서 물과 공기의 질량비율(또는 체적비율)이 계산 과정상의 상태와 달라지는 문제가 발생하게 되므로 LS법에서 재초기화 방법이 해에 영향을 주게 된다 (Scardovelli & Zaleski, 1999).
본 연구에서 수치 시뮬레이션의 대상으로 하고 있는 Spilling breaker는 해변이나 고속선의 선수주위에서 발생하는 쇄파현상으로, 파정에서 공기와 물 사이의 강한 운동량 교환이 일어나고 난류가 생성되어 파도 에너지가 소산된다. 표면장력이 약한 경우에는 공기가 물에 포획되거나 물방울이 공기 중에 튀어 오르는 현상이 발생하게 된다 (Duncan, 2001). 고속선의 선수주위에서 발생하는 spilling breaker는 선박저항의 최대 15%에 해당하는 에너지를 소산시키기도 한다 (Baba, 1969). Spilling breaker를 수치적으로 시뮬레이션하기 위해서는 자유수면주위에서 발생하는 급격한 속도 또는 압력의 구배를 구현할 수 있어야 한다. 이러한 문제에 VOF법과 LS법을 적용함에 있어서는, 가상의 천이영역을 얇게 유지하기 위하여 자유수면주위에 작은 격자를 사용하여 격자의 수가 과도하게 많아지거나 격자의 종횡비가 과도하게 커지는 문제가 발생하게 된다. Muscari and Di Mascio (2002a, 2002b)는 단상 LS법에서 spilling breaker를 시뮬레이션하기 위해 Tulin and Cointe (1986)의 가정을 이용하여 자유수면에 추가적인 압력과 전단응력을 부과하였다. 즉, Tulin and Cointe (1986)의 모델은 파고와, 수면경사 각, 프루드 수(froude number)를 이용하여 자유수면의 압력과 전단응력을 계산하는 것이다. Muscari and Di Mascio (2003)는 개발된 모델을 이용하여 실제 선박형상 주위의 spilling breaker를 시뮬레이션 하였다.
한편, Park, et al. (1999)이 제안한 밀도함수법에서는 자유수면을 물영역의 압력과 공기영역의 속도를 구속하는 경계면으로 정의하기 때문에 VOF법과 LS법에서 사용하는 가상의 천이영역을 갖지 않는다. 자유수면의 압력은 공기로부터 등가외삽으로 결정하고 자유수면 격자의 공기속도는 물의 속도로부터 라그랑지식으로 외삽하여 결정하게 된다. 밀도함수법은 물과 공기의 밀도와 점성계수로 각각의 유체영역에서 지배방정식의 해를 수치적으로 구해가지만, 자유수면의 압력과 속도를 상대 유체로부터 외삽하는 과정에서 오차가 발생하게 된다.
본 연구에서는 밀도함수법으로 자유수면에서 가상의 천이영역을 적용하지 않고, 자유수면 격자의 속도와 압력을 지배방정식으로부터 직접계산 하는 방법을 연구하였다. 해의 안정성을 위하여 자유수면에서 압력의 구배와 점성응력이 연속이 되도록 자유수면의 속도와 압력을 계산하였으며, 계산된 자유수면의 속도와 압력, 그리고 자유수면과의 거리를 사용하여 지배방정식을 계산하였다. 이렇게 수정된 밀도함수(modified marker-density, MMD)법을, 본 연구실이 보유하고 있는 INHAWAVE-II에 적용하여 2차원 수중익과 쐐기모양의 실험모델 주위에서 발생하는 spilling breaker 를 시뮬레이션 하였으며, 시뮬레이션 결과를 실험결과 및 Fluent V6.3의 결과들과 비교하였다.
지배방정식으로는 연속방정식(식 (1))과 Navier-Stokes방정식 (식 (2))이 사용되었다. 격자크기 이하의 유동의 난류특성을 고려하기 위하여 Subgrid-Scale(SGS) 난류모델을 적용하였다.
위 식의
지배방정식의 속도와 압력은 two-step projection기법으로 연성시켰다. 대류항의 공간 이산화에는 Kawamura-Kuwahara법이 사용되었으며, 시간 이산화에는 Adams-Bashforth법을 이용하였다. 나머지 항들은 공간에 대하여는 2차 중심차분법을, 시간에 대하여는 1차 전진차분법을 이용하여 이산화 하였다.
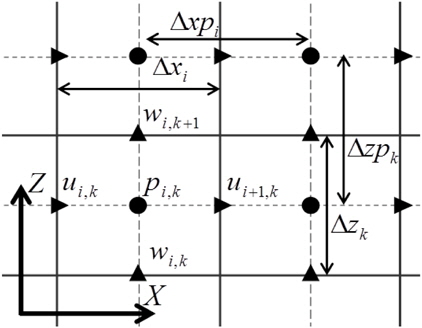
계산에 사용된 격자계는 직사각형 교차격자계로 격자면의 중심에 속도정의점이 있고, 격자의 중심에 압력정의점이 존재한다. 직사각형 격자계는 물체적합격자계(body fitted grid)와 달리 격자선과 물체면이 일치하지 않기 때문에 상대적으로 물체주위에서 계산의 정도가 낮은 단점이 있지만, 격자계 작성이 용이하고 이산화된 지배방정식이 단순하고 좌표계 변환이 필요 없어 계산 속도가 빠른 장점을 가지고 있다. 특히, 자유수면을 포함하는 문제에서 그 처리가 단순해지게 된다. 자유수면경계조건의 처리방법을 제외한 수치 해석 기법과 수치기법의 order of accuracy는 Lee, et al. (2012)와 Lee, et al. (2013)에서 그 자세한 내용을 찾아볼 수 있다.
자유수면의 경계조건을 수식으로 표현하면 식 (3)~(5)와 같다. 식 (3)은 자유수면의 운동학적 경계조건으로 자유수면에 수직한 방향으로 유체입자와 자유수면의 속도가 같다는 것을 의미한다. 식 (3)을 만족시키면 질량보존을 만족시키게 된다. 식 (4)는 자유수면의 접선방향으로 작용하는 힘의 크기와 방향이 물과 공기에서 같음을 의미하며, 식 (5)는 자유수면의 수직방향으로 작용하는 힘의 크기가 같고 방향이 반대임을 의미한다. 식 (4)와 식 (5)는 자유수면의 동역학적 경계조건으로서 만족시키면 운동량 보존을 만족시키게 된다 (Fergizer & Peric, 2002).
위식에서
자유수면의 운동학적 경계조건인 식 (3)을 쉽게 만족시키기 위하여 밀도함수의 수송방정식(식 (7))을 계산하고 자유수면의 위치는 물과 공기의 평균밀도를 갖는 위치로 정의하였다. 수송방정식을 이용하여 자유수면의 운동학적 경계조건을 만족시키는 것은 VOF법이나 LS법과 같다.
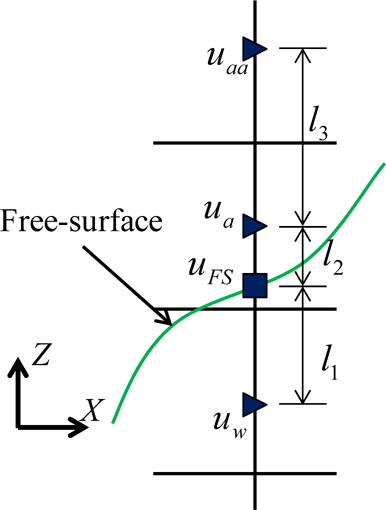
식 (4)를 만족시키기 위해서는 자유수면에서 점성응력이 연속이어야 한다. 물과 공기의 점성계수가 약 100배 차이나기 때문에 속도구배가 약 0.01배 차이가 나야한다. Fig. 2는 물격자와 공기격자 사이에 자유수면이 존재하는 경우를 1차원으로 단순하게 나타낸 그림이다. Fig. 2와 같이 물격자의 속도가
쇄파현상에서 표면장력은 공기의 포획이나 액적의 발생에 큰 영향을 주지만 이러한 현상을 시뮬레이션하기위해서는 1~2mm 이하의 아주 작은 격자를 사용해야만 한다. 이러한 작은 격자를 이용하여 선체주위 유동을 시뮬레이션 하는 것은 현실적으로 불 가능하므로, 본 연구에서는 실제문제에 적용가능성을 고려하여 자유수면의 운동학적 경계조건(식 (5))에서 표면장력의 효과를 무시하였다. 따라서 식 (11)을 만족시키면 식 (5)가 만족된다. 그러나 식 (11)만으로는 자유수면의 압력을 결정할 수 없다. 자유수면의 압력을 결정하기 위하여, 유동장의 속도분포가 시간과 공간에 연속이라고 가정하였다. 자유수면이 속도정의점을 통과하여도 그 속도정의점에서 속도가 연속이 되기 위해서는 지배방정식의 압력항과 확산항의 합이 연속적으로 변해야 한다. 그러나 압력항과 확산항의 합을 연속으로 만드는 것은 매우 복잡하기 때문에 절대값이 상대적으로 큰 압력구배항이 연속이 되도록 하여 식 (12)와 같은 경계조건을 추가적으로 적용하여 자유수면의 압력을 결정하였다.
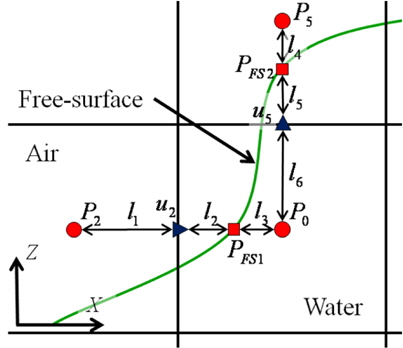
식 (12)는 Fig. 3과 같은 경우, 자유수면에서 공기와 물의 압력이 같은 식 (11)의 조건을 만족시키도록 자유수면의 압력을 이용하여 이산화하게 되면 식 (13)과 같이 표현 될 수 있으며, 식(13)을 정리하면 자유수면에서의 압력을 식 (14)와 같이 나타낼수 있다.
자유수면격자의 속도와 압력은 속도-압력 동시반복법을 이용하여 계산하였다. 자유수면의 속도는 속도정의점과 자유수면간의 거리와 자유수면의 압력을 이용하여 식 (15)와 같은 방법으로 계산하였으며, 자유수면격자의 압력은 발산을 이용하여 식 (16)과 같이 계산하였다.
위 식의
식 (9)의 자유수면 속도를 이용하여 자유수면에 이웃한 속도정의점의 확산항을 식 (10)과 같이 계산하고, 식 (11)과 식 (12)로 계산된 자유수면의 압력을 식 (15)에 대입함으로써, 실제 공기와 물의 밀도와 점성계수를 사용하면서 자유수면의 동역학적 경계조건을 만족시켰다.
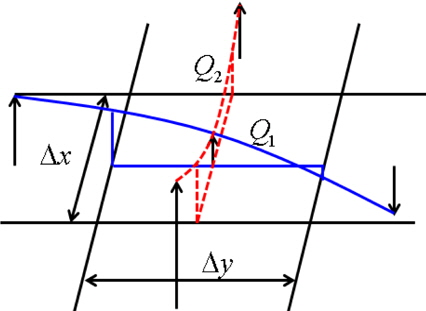
2차원 계산에서 식 (16)의 발산을 계산하기 위하여, 자유수면 주위 속도성분들의 분포가 2차 방정식을 따른다고 가정하였다. 2차 방정식은 이웃한 속도정의점을 이용하여 유도하고 적분하여, 각 격자면을 통과하는 유량을 계산하고 각 면의 유량을 더하여 발산을 계산하였다. 3차원의 경우 각 격자면의 유량 계산은 Fig. 4와 같이 격자면을 두 방향으로 계산한 유량을 산술평균하여 계산하였다.
식 (16)을 통하여 계산된 압력을 식 (15)에 대입하여 자유수면 주위의 속도를 재계산한다. 발산이 ‘0’에 가까운 값으로 수렴 할 때까지 반복하여 자유수면 격자의 압력을 계산하였다
3.1 수중익 뒤에서 발생하는 2차원 spilling breaker
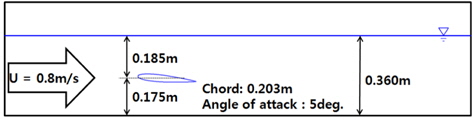
수치계산의 조건은 Duncan(1983)의 실험조건과 동일하게 설정되었다. 2차원 수중익의 단면형상은 NACA-0012이고, 받음각 은 5도, 유속은 0.8m/s이다. 수심은 0.360m이고 수중익의 중심은 수면으로부터 0.185m 잠겨있으며 수중익의 중심에서 바닥까지의 거리는 0.175m이다. 격자계의 종류가 달라 격자를 일치시키지는 못하였지만, 정수 중 자유수면에서 높이에서 격자의 크기가 0.002m로 일치시켰으며, 자유수면 주변격자의 크기는 4%씩 증가시켰다.
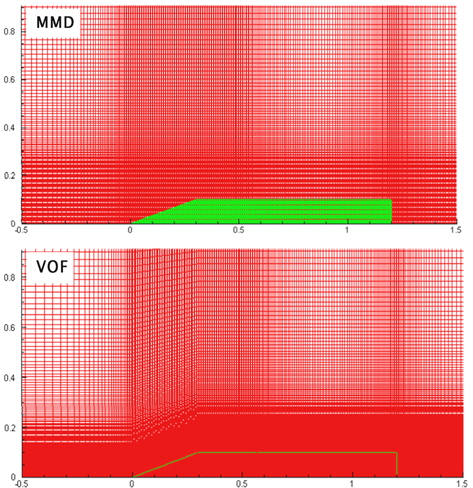
실험을 통한 Duncan (1983)의 연구결과에 따르면, Fig. 5와 같은 조건하의 첫 번째 파정에서 spilling breaker가 발생하였다. 한편, spilling breaker를 시뮬레이션 하기 위하여 Fig. 6과 같이 격자를 작성하여 MMD법을 적용한 INHAWAVE-II와 VOF법이 적용된 Fluent를 이용하여 수치시뮬레이션을 각각 수행하였다. 격자계의 영향을 최소화하기 위하여 각각의 계산에서 자유수면 주위 격자의 크기가 비슷하도록 작성하였으나, 격자의 종류가 서로 달라 완전히 일치시키지는 못하였다. Fluent의 계산에서는 Semi Implicity Method for Pressure Linked Equations(SIMPLE)을 이용하여 속도와 압력을 연성한 것과, K-ε 난류모델을 적용하였으며, 대류항은 Quadratic Upwind Interpolation for Convective Kinematics(QUICK)를 이용하여 이산화 하였다. 대류항의 이산화방법과 속도와 압력의 연성방법, 난류모델에 본 연구와 Fluent의 계산방법에 차이가 있다. 난류모델의 차이는 물체주위 국부적인 쇄파현상에 차이를 만들겠지만, 물체와 멀리 떨어진 자유수면에 미치는 영향은 작을 것으로 예상된다. QUICK법과 Kawamura- Kuwahara법은 모두 삼차상류차분법으로 대류항이 지배적인 문제에 충분한 정도를 갖는 것으로 알려져 있다. SIMPLE은 질량보존이 상대적으로 우수하고, two-step projection법은 운동량의 확산이 상대적으로 적은 것으로 알려져 있지만, 두 가지 방법은 자유수면 문제에 일반적으로 사용되는 방법으로 정상(steady) 문제에 만족할 만한 결과를 주는 것으로 알려져 있다 (Fergizer & Peric, 2002).
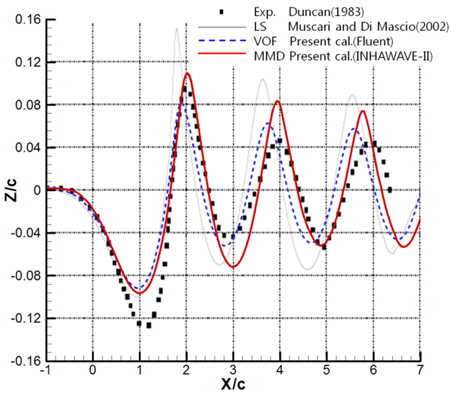
Fig. 7은 수치시뮬레이션을 통하여 얻은 자유수면의 2차원 형상을 비교한 것이다. Muscari and Di Mascio (2002a, 2002b)는 단상 LS법을 이용한 결과이고, Fluent는 VOF를 이용한 결과이다. LS, VOF, MMD법 모두 첫 번째 파저가 실험에 비하여 높게 나타나는 것을 볼 수 있으며, LS법과 VOF법의 결과는 파장이 실험에 비하여 조금 짧게 나타나는 것을 볼 수 있다. 이들에 비하여 MMD법은 실험에 근접한 파장을 보여주는 것을 볼 수 있다. 파고는 Fluent의 결과가 가장 실험에 근접하다. LS와 MMD의 파고가 높게 나타나는 것은 격자가 충분히 작지 않기 때문에, spilling breaker에 의한 공기의 포획이나 액적 등에 의한 에너지의 소산이 시뮬레이션 되지 않기 때문인 것으로 보인다.
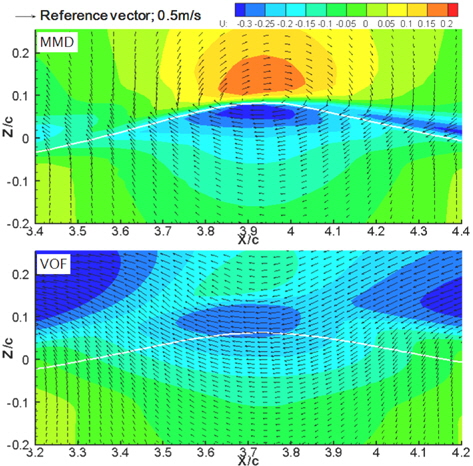
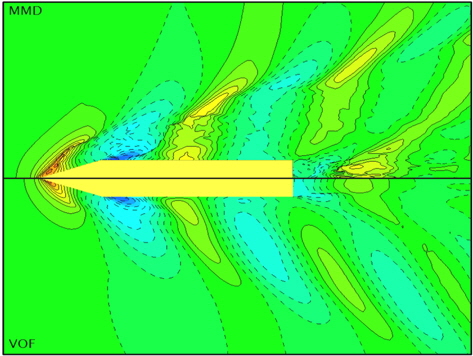
Fig. 8은 계산상의 두 번째 파고에서 X-방향의 속도분포와 속도벡터를 나타낸 그림이다. 파장이 서로 약간 달라 파정의 위치가 다르기 때문에 그림에서 X-방향이 위치에는 다소 차이가 있다. 그림에 나타난 속도는 유체의 속도에서 수중익의 전진속도를 빼서 표현한 것으로, 물의 유동이 우측에서 좌측으로 진행하는 것을 볼 수 있다. MMD법의 경우 파정에서 공기의 속도와 물의 속도가 서로 반대방향으로 나타나는 것을 볼 수 있지만, VOF법의 경우 물과 공기의 속도가 같은 방향으로 이동하는 것을 볼 수 있다. VOF법의 이러한 속도 분포는 공기와 물의 실제 밀도를 사용하지 않기 때문에, 자유수면을 기준으로 급격한 속도구배가 발생하지 않는 것으로 생각된다.
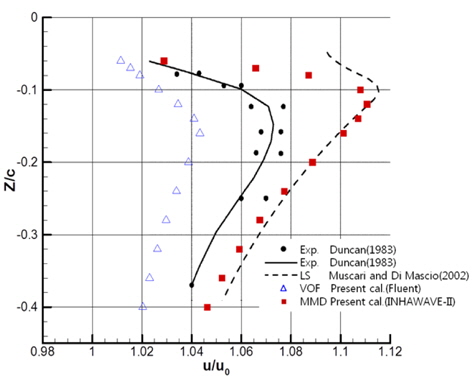
Fig. 9는 X/c가 5인 위치에서 수심에 따른 x 방향의 속도들의 분포를 나타낸 그림이다. VOF법을 사용한 Fluent의 경우에 속도가 가장 낮게 나타나고 있으며, 단상 LS법을 사용하는 Muscari and Di Mascio (2002a, 2002b)의 경우는 전체적으로 속도가 높게 나타나는 것을 볼 수 있다. MMD법의 결과는 Z/c가 -0.2이하인 경우 실험과 근접하고 있지만 그 이상에서는 실험보다 속도가 다소 크게 나타난다. 이러한 차이는 실제 실험에서 발생하는 공기방울과 스프레이에 의한 물과 공기 간 운동량의 교환과 운동량의 소산이 수치시뮬레이션에서는 나타나지 않기 때문인 것으로 생각된다. 본 연구에서 사용된 MMD법은 다른 수치기법에 비하여 파장을 잘 예측하므로 선수벌브와 같이 파도의 간섭이 중요한 문제에 활용하면 VOF나 LS법을 사용하는 것보다 좋은 결과를 줄것으로 생각된다.
3.2 쐐기형 모형선 주위에서 발생하는 3차원 spilling breaker
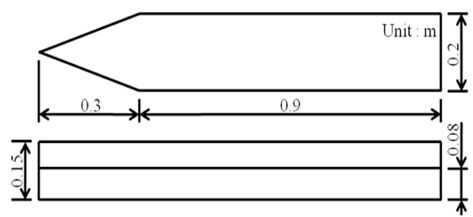
쐐기형 모형선의 선수와 선수부 어깨주위에서 발생하는 3차원 spilling breaker를 수정된 밀도함수법을 이용하여 시뮬레이션 하고, 실험결과 (Lee, et al., 2012) 그리고 VOF법의 계산결과와 비교하였다. 모형선의 형상과 주요제원은 Fig. 10과 같다. 수정된 밀도함수법과 VOF법을 이용하여 쐐기형의 모형선을 시뮬레이션하기 위하여 Fig. 11과 같이 격자계의 영향을 최소화 할 목적으로 격자의 크기를 서로 비슷하게 작성하였다. 모형의 전진속도는 1.0 m/s로 프루드 수는 0.319이다. 연직방향의 최소격자 크기는 0.004m로 일치시켰지만 다른 방향의 격자크기는 일치시키지 못하였다. MMD법에서 폭방향 격자의 0.004m이고, 길이방향은 0.005m이다.
Fig. 12는 수치계산을 통하여 얻은 등파고선도들이다. 선수와 어깨에서 발생하는 파도의 곡률이 두 가지의 계산 모두에서 급격하게 변화하고 있는 것을 볼 수 있다. 또한, MMD법을 사용하는 INHAWAVE-II의 수치계산 결과가 VOF법을 사용하는 Fluent의 결과에 비하여 파정이 높게 나타나는 것을 볼 수 있으며, 발산파의 각도가 더 큰 것을 볼 수 있다. 발산파의 각도에는 차이가 크지만 파장에는 큰 차이가 없는 것을 볼 수 있다.
Fig. 13은 실험에서 촬영한 선체 주위 파형과 MMD법 그리고 VOF법의 수치계산 결과를 비교한 것이다. 실험에서 선수와 선수 어깨 주위에서 spilling 형태의 쇄파가 발생하는 것을 볼 수 있다. MMD법의 수치계산 결과에서는 선수와 선수 어깨에서 발생하는 spilling 형태의 쇄파가 실험과 같이 파면의 경사가 크게 나타나는데 비하여 VOF법의 결과에서는 완만하게 나타나는 것을 볼 수있다. 선수어깨에서 발생하는 파도의 경우도 VOF법이 MMD법에 비하여 수면이 완만하게 나타나는 것을 볼 수 있다. Fig. 12에서 MMD법의 수치계산결과에서 Kelvin pattern의 파계가 선체에서 멀리 떨어진 곳에서부터 발생하게 되는데 이것은 Fig. 13에 보이는 것과 같이 선체주위에서 강한 비선형 파도가 발생하기 때문인것으로 생각된다.
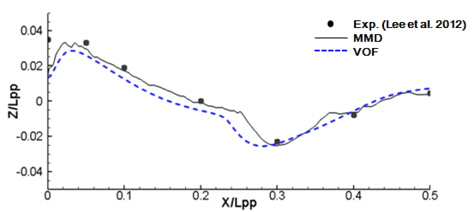
Fig. 14는 MMD법과 VOF법으로 얻은 선측파형을 실험결과와 비교한 것이다. 선수에서 VOF법의 결과가 MMD법에 비하여 약간 낮게 나타나며, 선수 끝단에서 두 가지 방법 모두 실험에 비하여 작게 나타나게 되는데 이것은 얇은 스프레이가 선측을 타고 오르는 현상을 수치적으로 구현하지 못하기 때문이다.
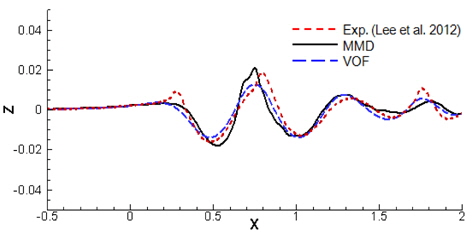
Fig. 15는 선체 중심면으로부터 우현으로 0.3m 떨어진 곳의 파형을 비교한 것이다. MMD와 VOF 모두 첫 번째 파정의 높이가 실험에 비하여 낮게 나타나는 것을 볼 수 있다. 두 번째 파정의 경우 파고와 파형은 실험과 MMD법이 서로 근접하지만 실험에 비하여 앞쪽에 있는 것을 볼 수 있다. VOF법의 경우는 파고가 다소 낮고 파형은 완만하게 나타나고 있다. MMD법은 전체적으로 파고를 높게 예측하게 되는데 이것은 2차원 수중익 계산에서와 같이 격자크기 이하의 액적이나 기포 그리고 표면장력의 효과 등을 시뮬레이션하지 못하기 때문인 것으로 생각된다. VOF법은 실험에 비하여 파고를 낮게 예측하게 되는데, 이것은 물과 공기의 실제 밀도와 점성계수를 사용하지 않기 때문인 것으로 여겨진다.
기존의 VOF법 또는 LS법은 유체의 성질을 공간적으로 변화시켜 자유수면의 동역학적 경계조건을 만족시켰으나, 본 연구에서는 밀도함수법을 수정하여 압력구배와 점성응력이 연속이 되도록 자유수면의 속도와 압력을 계산하였으며, 지배방정식 계산에 자유수면의 속도와 압력을 적용함으로써 가상의 천이영역 없이 자유수면을 모델링하였다.
MMD법을 이용하여 2차원 수중익 뒤에서 발생하는 spilling breaker를 수치 시뮬레이션 한 결과, 기존의 방법들에 비하여 실 험에 근접한 결과를 보임을 확인하였다. 또한, 쐐기형의 모형선 주위에서 발생하는 3차원 spilling breaker를 MMD법과 VOF법으 로 시뮬레이션 하여 기존의 실험결과와 비교하였다. 파형을 실험 사진과 정성적으로 비교하면, MMD법이 VOF법보다 정성적으로 실험에 근접한 결과를 보이는 것을 알 수 있다. 선체주위의 비선형 쇄파로 인하여 MMD법에서는 Kelvin pattern의 파계가 선체에서 떨어진 곳에서 발생하게 되지만 VOF법에서는 쇄파현상이 약하게 시뮬레이션 되어 선체주위에서부터 발생하게 된다. 같은 이유로 선체표면에서의 파고도 MMD법이 실험에 더 근접하게 나타나고 있다. 그러나 선체 중심에서 0.3m 떨어진 곳에서 측정한 파형은 서로 비슷한 오차를 보이고 있다. 이러한 이유는 MMD법의 경우 액적이나 기포, 표면장력 등에 의한 파 에너지의 감쇠현상이 약하게 나타나고, VOF법은 실제밀도를 사용하지 않아 파고가 낮게 나타나기 때문인 것으로 여겨진다.
본 연구에서 개발된 수치기법은 해양구조물이나 선체주위의 쇄파현상을 연구하는데 기존의 계산기법 보다는 보다 더 유용하게 활용이 가능할 것으로 생각된다. 특히, 고속선의 구상선수와 같이 쇄파가 예상되고 파 간섭이 중요한 문제에는 그 활용도가 높을 것이다.