To raise the industrial competitiveness in the field of ship-building, it is crucially important that the yard should use production facilities and working space effectively. Among the related works, the management of tremendous blocks’ number, the limited area of assembly shops and inefficient personnel and facility management still need to be improved in terms of being exposed to a lot of problems. To settle down these conundrums, the various strategies of block arrangement on the assembly floors have been recently presented and in the results, have increasingly began to be utilized in practice. However, it is a wonder that the sampled or approximated block shapes which usually are standardized projections or the geometrically convex contour only have been prevailed until now. In this study, all parts including the panel, stiffeners, outer shells, and all kinds of outfitting equipment are first extracted using the Volume Primitive plug-in module from the ship customized CAD system and then, the presented system constructs a simpler and more compact ship data structure and finally generates the novel projected contours for the block arrangement system using the adaptive concave hull algorithm.
선박은 순수 형상적인 측면에서 외판, 내판, 그리고 의장품으로 구분할 수 있다. 이들의 형상적 조합은 조선 생산과정에서 다양한 용도로 활용될 수 있으며, 본 연구에서는 정반블록 배치를 위한 블록 투영 형상 추출과 증강현실(augmented reality, AR)을 이용한 선체 검사용 프로그램 개발에 초점을 두고 시작되었다. 다시 말해, 선체를 세밀하게 혹은 정밀하게 표현하기 보다는 모바일 기기를 통한 전송시간과 계산시간을 줄여서 신속한 대응이 가능하도록 하는 것이 목표이다. 본 연구에서는 정반 배치용 블록 투영 형상을 획득함에 있어서 모바일 기기로의 전송 시간을 절약하기 위해 추출 모델링 정보를 간략화하려고 노력하였으며, 계산시간을 줄이기 위해서 실시간 투영 형상 획득이 가능한 알고리즘을 제시한다.
Hur (2012)는 그의 석사 논문에서 생산성 향상을 위해 정반조립공정을 통합된 하나의 시스템으로 제공하였다. 이를 위한 과정에는 정반 배치 시, 기초 정보로 활용하기 위해 블록의 3D형상을 2D화해서 표현해야하는데 이를 자동화하기 위해서, Tribon M3 (Tribon M3, 2014)의 Plug-In 모듈의 하나인 Robot Interface(ATX format)을 활용하였다. 본 모듈은 추가 라이선스를 통해서만 구입할 수 있으며, 결정적인 단점은 외판 및 의장 추출을 지원하지 않는다는 점이다.
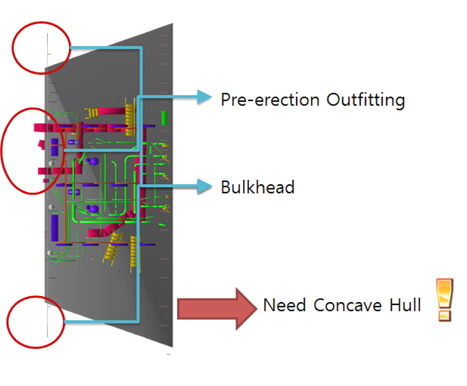
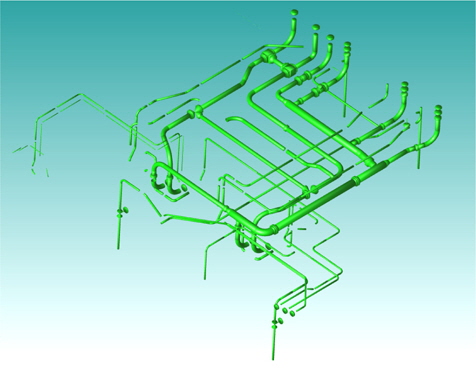
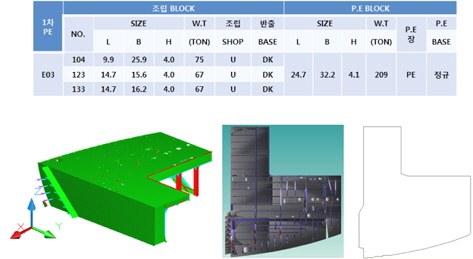
도크, 안벽 관련 생산 공정에서 의장 관련 작업부하를 분산시키기 위해서 특히 엔진 블록의 배관(Heating coil, F.O Line 등)들은 외판이 덮이면 작업이 어렵기 때문에 의장 설치와 블록 조립 작업을 병행하게 된다. Fig. 1과 같이 보통 선행의장의 精度가 탑재공기 절약에 큰 영향을 미치기 때문에 최대한 많은 양의 작업을 미리하려는 것이 요즘 추세이다. 본 논문에서는 대조립 공장의 정반 배치에 사용되는 블록 투영 형상에는 당연히 외판과 선행의장이 포함되어서, 볼록 형상으로 근사하기 보다는 배치의 정밀도를 보장하는 오목형상으로 나타내어야 한다고 생각하였다. Fig. 2에서는 예제로 엔진룸 데크를 위에서 조망하였을 때, 볼록 형상으로는 해결하기 난감한 의장품과 기타 횡단부재들을 보여준다.
정반배치용 블록 형상의 볼록화는 해당 투영 형상을 얻기는 쉬우나 정반이나 PE 장에서의 정밀한 배치를 방해하며 낭비되는 공간을 증가시킬 우려가 있다. Koh, et al. (1999)은 그의 논문에서 정반 배치 시 작업공간의 확보에 관해서 언급하고 있는데 블록의 근사 볼록 다각화 형상에만 집중하였다.
Park (2013)의 석사학위 논문에서는 위에서 언급된 ATX 모듈로 추출이 안 되는 외판의 형상과 의장품의 정보를 위해 3D DXF 형식으로 완성된 블록의 형상을 획득할 수 있었다. 하지만 DXF 타입의 추출방법은 추출 결과의 용량이 일반 상선의 경우 3 GByte를 쉽게 넘어설 정도로 현 컴퓨터 환경에서도 무리가 따른 다. 또한 다양한 추출 모듈(ATX, DXF, SX700)을 사용하여 시스템의 복잡도가 증가되고 그에 따른 오류의 가능성도 무시할 수 없다. 물론 3차원 형상을 일정한 요소로 세분화하는 Tessellation의 형태로 데이터를 제공하므로 구조해석 혹은 다양한 물체 정보 획득에 활용할 수 있는 이점은 분명 존재한다 (Jo, et al., 2011). 하지만 모바일 환경에서의 선체 형상 정보의 원활한 전송에는 큰 무리가 예상된다. 추출된 선체정보에 큰 부담은 평판보다는 주로 곡판이나 곡형부재들인데 그들이 대부분 외판과 의장품들이 연관되어 있다. 평 블록과 달리 곡 블록은 기준 판(base plate)의 정보로 배치 방향이 정해지지 않고 그 형태의 특수성으로 인해 Pin Jig가 설정된 고정된 위치로 확정 된다 (Koh, et al., 1998). 결국 평블록 및 곡블록의 정반 배치용 블록 투영 형상을 확보하기 위해서는 해당 블록의 조립방법을 설명하는 DAP(detailed assembly procedure) 도면과 Pin Jig 도면에서 정보를 확보해야 한다. 정반 배치 자체에 관한 연구는 Lozano-Perez (1983), O’Rourke, et al.(1982), Lee, et al. (1996), Um (2008) 등이 있는데 모든 블록 형상은 볼록 형상에 머물러 있다.
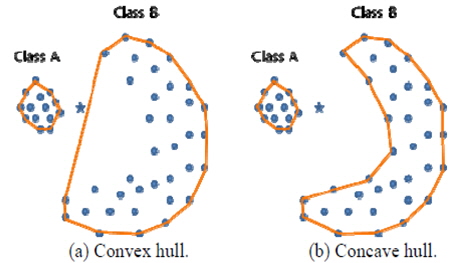
기존에 주로 사용되었던 볼록 형상(convex hull)이란 평면상에 놓인 유한한 점들의 집합을 모두 포함하는 최소한의 볼록한 형상을 유지하는 경계선들의 집합이라고 정의할 수 있다. 이는 패턴 인식, 이미지 프로세싱, 통계, 조선분야에서는 네스팅 알고리즘 등을 포함한 많은 응용 분야에서 사용되고 있다. O’Rourke(1994)의 저서에도 설명되어 있듯이 잘 알려진 볼록 형상의 구현은 “Graham’s Scan”과 “Jarvis’ March” 정도 이다.
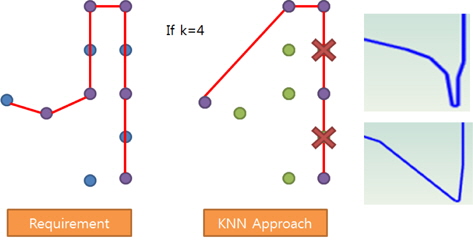
Fig. 3에서도 확인할 수 있듯이 볼록형상(Fig. 3(a))은 해당 형상의 특징을 정확하게 반영하고 있지 못하며 우측에 있는 오목형상(Fig. 3(b))이 정확한 분류 기준을 마련하고 있음을 알 수 있다. 최근에 오목 형상 추출에 관해서는 ‘Swing Arm’ (Galton & Duckham, 2006), ‘
정리해보면, 본 논문에서는 조선전용 CAD 프로그램 중 하나인 Tribon M3의 Plug-In 모듈을 활용하여 Volume Primitive Data(3차원 형상을 위치, 크기, 방향 정보만을 이용하여 최대한 간단하게 표시하는 방법)를 확보하고, 데이터의 용량을 극도로 경량화하기 위해 외판을 Hull Curve의 일부만 이용하여 NURBS(Roger, 2001) Surface 형태로 생성하였으며 의장품에 LOD(Luebke, et al., 2003)를 적용하였다. 또한 GIS 연구분야에서 발전된 kNN기반 오목형상 추출법을 발전시켜 정반배치용 블록 투영 형상을 확보할 수 있는 알고리즘으로 개선하였다. 이에 관한 활용 예로 외판, 내판, 의장품을 모두 포함하는 블록 형상의 투영 오목 다각형(concave hull)을 생성하였다.
본 논문은 다음과 같은 순서로 전개된다. 2절에서는 조선 전용 CAD 시스템에서의 간략 형상 정보 추출과 경량화에 관해서 3절에서는 정반 배치 블록 투영 형상을 위해 개선된 Concave Hull의 알고리즘을 구체적으로 설명하고, 4절에서는 블록의 2차원 정반 배치용 투영형상 추출 사례에 관해서 설명한다. 마지막으로 본 연구의 결론과 개선점들이 기술된다.
2.1 Volume Primitive를 이용한 정보 추출
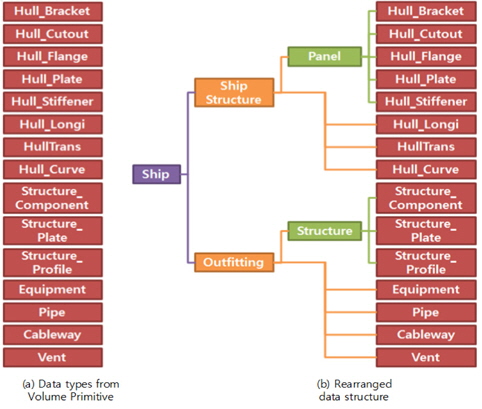
조선 전용 CAD에서 확보한 Volume Primitive Data 내에서 정의되는 데이터의 형식은 Fig. 4(a)과 같다. 이를 개발하고자 하는 본 프로그램에 표현하기 위해, 크게 Ship_Structure 라고 하는 선체부와 Outfitting이라고 하는 의장부로 분류하고, 이를 세부적으로 분류하여 Ship_Structure의 경우에는 Panel, Hull_Longi, Hull_Trans, Hull_Curve로, Outfitting의 경우에는 Structure, Equipment, Pipe, Cableway, Vent로 나누었으며, Ship_Structure 와 Outfitting 모듈의 모임이 선박 한척을 표현하도록 하였다 (Fig. 4(b)).
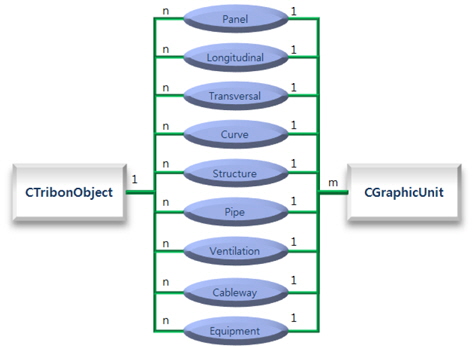
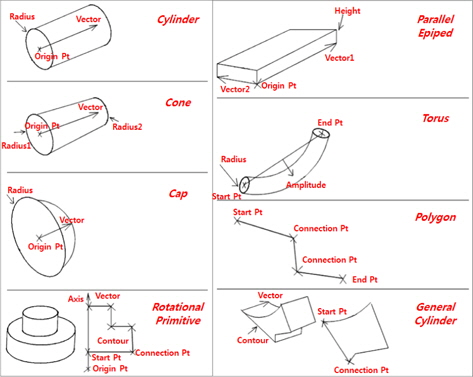
Fig. 4(b)의 계층구조에서, Fig. 5의 Tribon_Object Class와 같이 최하단 단위들은 조선용 부재로써의 생산정보를 가지는 마지막 단계이며 이에 속하는 이후 모듈은 Fig. 5의 Graphic_Unit Class처럼 형상정보들만을 가지게 된다. 형상정보만을 가지는 최소 단위는 Volume Primitive가 가지는 원형을 Fig. 6와 같이 그대로 유지했다. Volume Primitive는 모든 형상들을 Fig. 6의 반시계 방향 순으로 cylinder, cone, cap, rotational cylinder, general cylinder, polygon, torus, parallelepiped 로 표현하고 내부재와 의장품을 간결하게 정의할 수 있게 한다. 자료구조 측면에서 볼 때, 나열된 형상들은 Graphic_Unit이라 명명된 가상 선조 클래스를 통해 상속받아 쓰인다. 가상 선조 클래스는 객체지향 언어의 개념으로, 관련된 클래스들을 하나의 선조로 묶어주는 역할만 하고 자체로는 구현이 안 되는 클래스를 의미한다.
추출된 Volume Data는 n개의 Tribon_Object로 구성되며, Tribon_Object의 종류로는 실제로 다루고자 하는 Panel, Longi., Trans., Curve, Structure, Pipe, Vent, Cableway, Equipment 등의 유형이며, 각각의 Tribon_Object는 Fig. 5과 같이 m개의 Graphic_Unit으로 구성 된다. 외판을 생성하기 위한 Hull_Curve의 경우에는 DB에 Tribon_Object로 존재하지만, 시각화 시에 Surface로 전환되어서 외판을 구성하는 방식을 따른다.
다시 언급되는 것이지만 조선전용 CAD에서 선체모델의 경량화 추출은 정반 배치용 블록 투영형상 생성과 모바일 기기를 통한 선체 검사 목적으로 개발되었다. 블록이 가지는 3차원 형상의 정밀도보다는 전송속도 그리고 계산시간 절감에 그 초점이 있음을 다시 한 번 밝힌다.
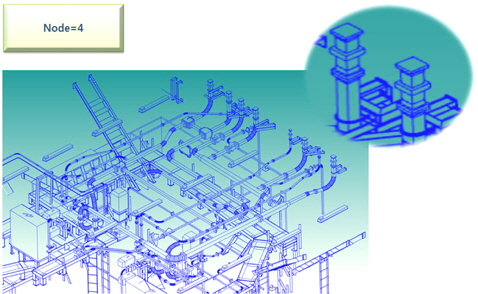
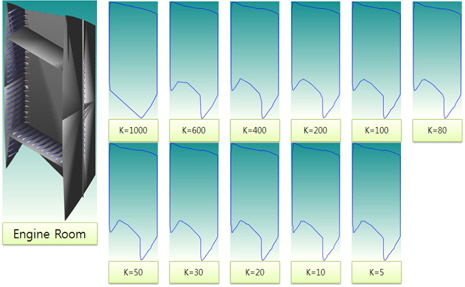
Primitive Volume이 표현하는 형상적인 측면에서의 그 용량은 더 이상 경량화 할 수 없을 정도로 간결하다. 다만 평판이 아닌 곡면 형상을 가지는 부재를 표현할 때 주어진 호(Arc)에 따른 형상 변화를 어떤 정밀도로 표현하는 가에 따라서 가시화되는 정밀도와 크기 사이에 적절한 조절이 필요하고 이는 LOD의 영역이다. 시작점과 끝점 그리고 고정된 호의 크기(amplitude)를 가지는 곡형은 노드(N개)의 점들로 Polygon을 구성하게 된다. 본 연구에서 는 Fig. 7과 같이 엔진 블록의 일부 파이프 모듈을 선택하여 다양한 추출방법과 N의 값을 달리해 가면서 파일 크기의 차이를 검토했다. 또한 Fig. 8에서는 N의 값이 최소값으로 설정된 4일 때의 의장 모듈이 어떻게 표현되는지 나타내고 있다.
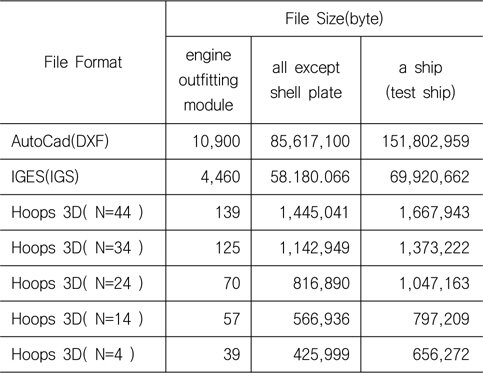
Table 1은 Tribon M3가 지원하는 AutoCad(DXF), IGES(IGS), 그리고 추출된 형상의 노드 수를 변경하면서 생성된 Hoop 3D(HSF) (HOOPS Exchange, 2014)파일 크기를 각각 비교하고 있다. 총 3경우에 관한 것을 비교하고 있는데, 엔진룸 부근의 파이프 모듈, 외판을 제외한 모든 내부재와 의장품, 마지막으로 외판까지 포함하는 한 호선에 관한 비교이다. Tribon M3에 담겨있는 테스트 호선임에도 불구하고 한 호선 전체의 DXF의 출력량은 150Mb정도임을 확인할 수 있었다. 그에 비해 외판, 내판, 의장품을 모두 포함해서 한 호선을 가시화하여 HSF (HOOPS Exchange, 2014)파일 포맷으로 저장하였을 때 1Mb 근처 정도였다. 모바일기기가 선체 가시화의 대상으로 확장되는 추세에 맞춰서 본다면 본 연구방식의 접근법이 상당히 적절한 것으로 판단된다.
[Table 1] File size and LOD comparison for a test ship
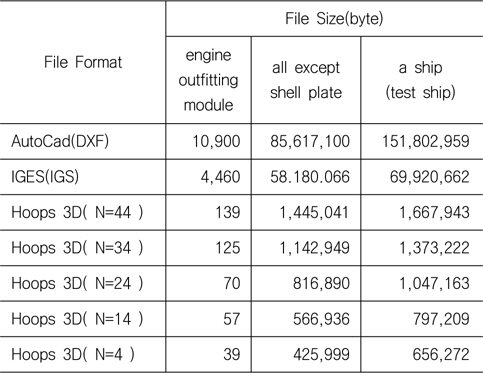
File size and LOD comparison for a test ship
선체 형상을 간략하게 표현하기 위해서 가장 큰 문제가 되는 것이 외판이다. 여기서 외판을 간략화를 시키는 목적은 구조해석, 선체 거동 등의 해석영역을 해결하려는 것이 아니고 전송 속도 및 계산 속도를 고려한 형상 파악이다. 이를 위해서는 정밀도를 약간 희생하더라도 추출된 파일 크기를 최소화한다. 일반적으로 모델링된 Hull Curve를 살펴보면 Knuckles, Tangents, Sections, Water lines, Buttocks, Boundary curves, Diagonals, Deck Frames로 구성된다. Fig. 9를 보면 선박의 선형정보 외에도 참조선을 추가하여 이후 상세 설계의 경계정보로 활용되기도 하며 이외 설계자가 임시적로 정의한 라인이 많이 존재하여 추출하기에 많은 애로점이 존재한다.
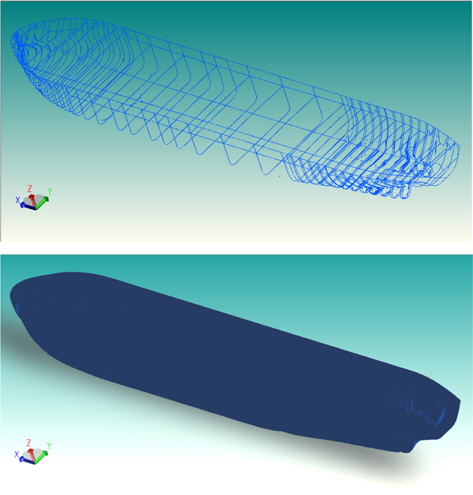
본 연구에서는 Fig. 10과 같이 간략한 외판 정보를 획득하기 위해서 과감하게 Section에 관련된 Hull Curve만을 대상으로 한다. 이를 대상으로 Port/Starboard 방향과 開곡선인지 閉곡선인지 선수/선미 방향인지 구분하고 정렬하여 NURBS Surface의 입력 데이터로 활용한다. 주어진 Hull Curve로 NURBS를 만들기 위해서는 Tensor Product 방법으로 접근하였을 때, u 방향 혹은 v 방향 중 한 방향으로 각각의 Curve들이 균일한 점의 수를 가져야 하는데, Volume Primitive으로 주어진 Hull Curve들은 주어진 구간에서 주변의 Curve들과 일반적으로 동일한 노드수를 가지지 않는다.
연속된 Curve들의 수를 M 개라 하자. 이는 사용자가 지정할 수 있는 파라미터에 해당하고 Surface를 이루려고 하는 Curve들은 같이 노드수를 가져야 하므로, M중에 최대 노드수를 가지는 Curve의 노드수와 일치시키기 위해서 나머지 Curve들의 Node 수를 해당 Curve를 따라 균일하게 새롭게 배치하였다. NURBS를 구성하기 위한 가중치는 모두 1로 통일하고 차수는 3차 이하로 그리고 ‘Open Uniform Knot Vector’ ( 0, 0, 0, 1, 2, 3, ... , n, n, n )를 활용하여 선택된 모든 점들이 구축된 Surface에서 C2 레벨의 연속성을 가지도록 설정하였다. Fig. 11는 Surface를 구성하기 위한 연속된 Curves의 개수(M)를 5로 설정하고 Volume Primitive를 통해 추출된 Hull Curves를 통해 NURBS Surface(Fig. 11의 하단)와 그에 해당하는 Wire-frame(상단)을 표현하고 있다. Fig. 12는 같은 조건으로 선수미 부근을 확대해 본 그림이다. DXF를 통한 추출 결과와 정밀도를 비교하면 곡이 심한 선수미 부근에서 정밀도 측면에서 약간 부족한 면이 있지만, Table 1에서 확인할 수 있듯이 계산 시간과 파일 크기 면에서는 비교할 수 없을 정도로 추출 시간(DXF:11분 소비, Volume Primitive: 1.2초 소비)과 크기가 축소됨을 확인할 수 있었다. Fig. 11과 12을 통해서 본 논문에서 제안하는 선체외판이 선수미 블록의 투영 형상을 얻어 내기에 무리가 없다고 판단하였다.
정반배치용 투영형상의 획득은 전체 선형을 참조로 하는 것이 아니고, 예제로 설명될 각 블록별 외판 형상이 참여되는데 이를 위해서는 선택된 블록의 X, Y, Z방향의 박스 경계 값을 입력받아서 박스에 소속된 Hull Curve의 노드들만 필터링하여 새롭게 Hull Surface를 구성하였다. 이에 관한 설명은 4장에서 구체화된다.
3.1 The Adaptive Concave Hull Algorithm
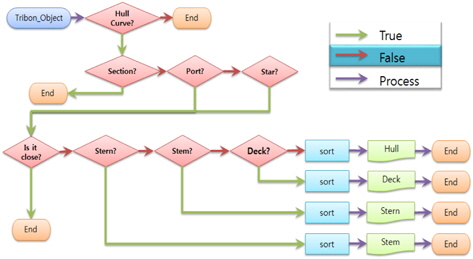
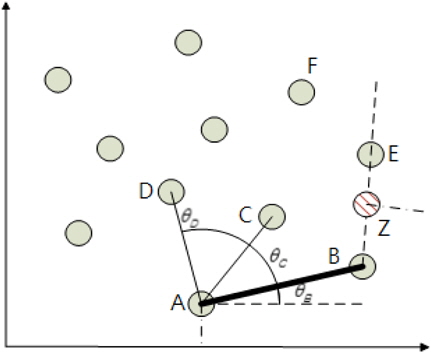
우선 Convex Hull 알고리즘 중에 Jarvis’ March(일명 Gift wapping algorithm)방법은 Fig. 13와 같이 최하단 최좌측점을 시작점으로 삼고, 무한히 긴 회전 가능한 팔(swing arm)을 돌려서 가장 먼저 닿는 점들을 잇는 방법이다. 여기에 kNN 즉 현재 점을 중심으로 가장 가까운 이웃 k개만을 대상으로 Javis’ March 방법을 응용하면 국부적인 특징이 살아나면서 Concave Hull을 추출할 수 있다는 것이 Moreira and Santos (2007)의 아이디어였다. 이는 GIS(geographic information system) 분야에서 종사하는 이들이 분포하는 점들의 경계를 획득하려는 시도로 이루어졌다. 예를 들자면, 범죄자의 휴대폰 이력을 조사하여 활동범위를 한정하려는 목적이 대표적인 예이다. 우선 kNN에서 k값이 전체 점의 수와 같다면 Convex Hull을 구하는 Jarvis’ March의 접근방법과 일치한다. 최소값이 3인 k값이 전체 점의 수보다 적으면 적을수록 정밀해지며 다시 말해 오목해 진다. Fig. 14에는 여러 점이 있는데 Solid 점만 고려하고 일단 차후에 설명될 빗금 점은 무시하자. 우선적으로 y값이 가장 적은 점을 선택한다. 만일 y 최소값을 갖는 점이 여러 개이면 그 중에서 가장 작은 x 값을 가지는 점(Point A)을 선택하고 이를 Concave stack에 보관한다. k를 3으로 가정한다면 가장 가까운 3개의 점(B, C, D)을 찾을 수 있다. 후보 점들을 평가하기 위해서 점선 기준선을 이용하여 오른손 법칙으로 각도들(𝜃
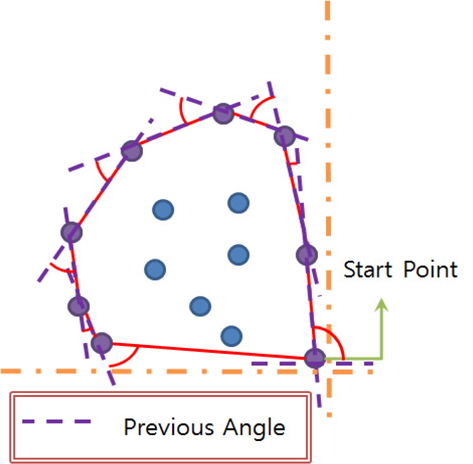
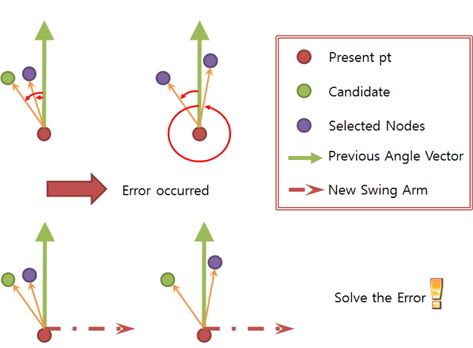
우선 위의 접근방식에는 가정이 필요한데, 어떠한 연속된 3점도 일직선이 되어서는 안 된다. 하지만 본 연구 대상인 블록 Concave Hull의 많은 부분은 연속된 점들이 일직선 관계를 유지한다. Fig. 14의 빗금으로 채워진 원이 이에 해당한다. B가 기준점일 때 Z 보다는 E를 선택 하면 결과적인 Concave Hull이 간략화 될 것이 분명하다. 그러므로 같은 각도를 가지는 Z점은 무시되고 기준점(B)에서 같은 각도를 가지는 많은 후보점들 중에서 가장 먼 점(E)을 선택 한다. B점은 다음 후보점군에서 제거 되지만 Z점은 Concave Stack에 선택되지 않았지만 제거하면 안 된다. 만일 제거하게 된다면 의장품과 같이 세장비가 긴 형상을 유지하지 못하는 경향이 발생된다. Fig. 15에서는 제거했을 때 발생할 수 있는 문제점과 안했을 때의 개선점을 설명하고 있다. GIS 분야에서는 의미 없었던 문제점이 조선분야 응용에는 빈번하게 발생되는데 특히 세장비가 긴 형상을 가지는 의장품을 포함하는 블록의 형상을 얻어내는데 큰 기여를 하였다.
기존 방법의 또 하나의 문제점은 각도 평가에 사용되는 기준선을 마지막 선택 점에서 현재 점으로 이어진 vector로 사용하면, 일직선상에 많은 점이 놓여 있는 경우, 원하는 방향으로 가지 못하고 엉뚱한 결과물을 얻어 내는 경우가 빈번하였다. 이는 Fig. 16의 상단처럼 기준선의 방향이 일직선 방향의 부근점을 평가할 때 최소값을 주지 못하고 오히려 최대값을 주는 현상 때문이었다. 그래서 본 연구에서는 Fig. 16의 하단 과 같이 간단한 외적 연산을 이용, 일점쇄선과 같이 기준선을 바꿔서 항상 올바른 평가가 이루어질 수 있게 하였다.
그 외 주목해야 할 점은 k의 값의 선택이다. k값이 주어진 문제에서 결과를 얻어내기에 어려운 경우, 기준 점 근처에서 선택된 후보군들 중에서 선택할 가치가 없어서 더 이상 Concave Hull를 구성할 수 없는 경우에는 Algorithm이 이를 자동으로 증가시키게 하였다. 다음 장에서 설명될 정반 배치용 투영형상을 얻기 위해서는 사용자는 해당 블록과 선행의장품을 추출하고 이를 기반으로 형상을 얻게 된다. 하지만 사용자의 의도와 달리 해당 블록과 관련 없는 의장품이 추출되는 경우, 즉 블록을 이루는 영역 외에 다른 부재 혹은 점들이 존재한다면 원하지 않는 해가 될 것이며, 이는 패턴인식 분류(Clustering, Shared Nearest Network 등)를 이용하여 영역을 분리하는 과정이 필요하며 본 논문에서는 언급하지 않는다. 한편, 본 알고리즘의 종료조건은 처음 선택된 점(A)이 진행하면서 다시 선택되었을 때 프로그램은 마무리된다. 이를 위해서는 첫 점(A)만은 예외적으로 후보군에서 제거하지 않는다.
블록 대조립 공장의 정반회전율은 도크회전율과 더불어 조선소 생산성 향상을 위한 주요 요소 중 하나이다. 기존에는 경험이 많은 현장 작업자가 블록의 2D도면 또는 표준형상을 이용하여 수작업으로 배치 작업을 수행하였지만 최근 자동배치 알고리즘에 관한 다양한 연구가 진행되고 있다 (Jo, et al., 2011; Koh, et al., 1999). 하지만 지금까지의 연구는 획득한 투영 형상이 선행 의장품들을 포함하지 못하고 그 형태가 획일적으로 모두 볼록(Convex)형상이다. 본 연구에서는 블록 투영형상을 얻기 위해서 kNN(k nearest neighborhood, Beyer, et al., 1999)기법을 이용하여 블록형상(convex hull, Devroye & Toussaint, 1981) 알고리즘을 오목형상(concave hull)으로 전환시키는 방법을 개선하여 더욱 정밀한 블록 투영 형상을 확보하려 한다.
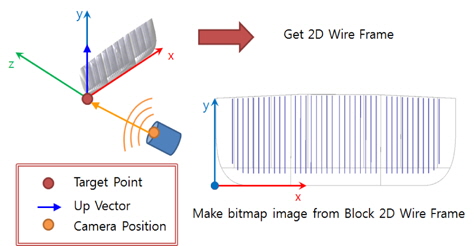
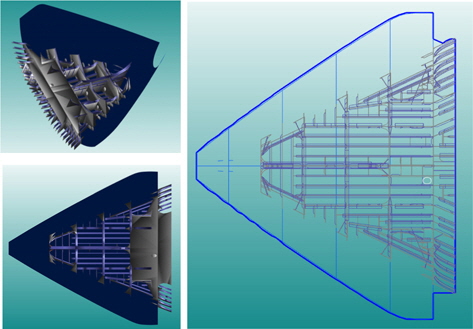
기존에 투영형상을 얻어내기 위한 방법은 추출된 모든 부재별로 기준면에 투영좌표를 확보하고 기준점을 중심으로 회전하면서 가장 멀리 떨어진 점을 확보하는 방식이라면 3장에서 설명한 알고리즘을 적용하기 위해서는 Concave Hull을 추출하기 위한 해당 블록 영역을 표시하는 Point set만을 확보하면 충분하다. Fig. 17에서와 같이 up-vector와 타겟 및 카메라 포인트를 지정으로 base plate의 방향을 지정하면 블록의 정사 투영 형상(orthographic projection)이 확보되는데, 계산에 기초가 되는 후보점들을 줄이기 위해서 Solid한 투영형상을 이용하지 않고 이를 Hoop3D 라이브러리를 이용하여 Wire-frame 으로 전환시킨다. 변경된 Wire-frame을 화면 캡처해서 비트맵이미지를 만들어 이에 scale을 적절하게 지정하면 입력을 위한 Point set이 준비된다. 상술하면, Fig. 18의 우측에 표현된 Block을 이루는 모든 점(외판선, 내부재, 의장품을 이루는 모든 선을 구성하는 모든 점을 뜻한다.)들은 후보점으로 변환되며, 외곽의 굵은 선으로 표현된 점들이 최종 결과물에 해당한다. Fig. 18의 좌측에는 선수 블록의 임의 각도의 View와 Deck View가 표시되어 외판까지 포함하는 해당 블록의 형상을 파악하는데 도움을 주려하였고, 우측에는 위에서 설명한 바와 같이 모든 부재를 포함하는 투영 다각형 형상이 굵은 색으로 산출되었다.
마지막으로 실무에서 사용되는 다양한 블록들을 대상으로 계산시간을 체크해 보았다. 그 중 Fig. 20에서 보인 바와 같은 Bulk carrier deck block 예제를 포함하여 테스트한 모든 블록이 0.1초 내로 투영형상을 얻어낼 수 있음을 확인하였다.
본 논문에서는 실시간 정반 배치용 투영 형상을 얻어내기 위한 방안에 관해서 논하고 있다. 모바일 기기로의 선체 형상 정보를 송출하기 위해 정보를 간략화할 필요가 있는데, 조선 전용 CAD 시스템으로 모델링된 선체의 내판, 외판, 의장품의 간략 형상을 추출하고 DB 형태로 자료 구조화하는 방안에 관해서 설명하고 있다. 추출 형상 데이터를 최소화하기 위해서 Volume Primitive의 활용과 곡형 표현을 다각화하였고, NURBS Surface를 활용하여 외판 표현을 간략화 하였다. 이를 바탕으로 기존 연구와 달리 의장관련 부재들을 포함할 수 있었다. 또한 블록 투영형상 계산 시간의 절감을 위해 오목형상화를 정반 배치용 투영형상으로 특화하여 기존에 사용되었던 정형화 샘플이나 볼록 블록 형상과 비교하여 정밀한 형상과 면적을 산출할 수 있는 다각형을 확보할 수 있었다. 이를 위해서 kNN과 Convex Hull algorithm을 조합한 기존의 알고리즘을 개선하였고, k값의 조절로 작업자가 원하는 정밀도의 오목다각형을 최대한 간결한 형태로 추출할 수 있는 새로운 방안을 제시하였다. 사용자는 원하는 블록 혹은 블록의 조합에 관하여 놓일 각도만 입력하면 간편하게 자동으로 정반 배치용 형상을 추출할 수 있다. 지속적인 연구 발전을 위해서는 사용자의 개입이 없어도 도면 혹은 설계 DB 및 ERP시스템과 연계하여 Base Plate 혹은 Pin-Jig 관련 정보를 자동으로 확보하게 하고, 같은 LOD를 유지하면서 보다 정밀한 외판을 확보할 수 있는 개선 작업을 수행할 예정이다.