자연계에서 군집(formation) 생활을 하는 생물들은 먹이 찾기, 적에 대한 방어, 보금자리 짓기 등 군집 행동을 통해 복잡한 문제를 해결할 수 있다. 이러한 생물의 군집 행동을 응용해 여러 가지 문제를 해결하기 위한 연구가 진행되었다. 최근에는 군집 제어로 하는 미로 탐색, 협력 운반, 전투기 자율 비행 등, 군집제어는 다양한 분야에서 널리 연구되어 왔다[1].

이동 로봇의 군집 제어에 대한 연구는 크게 가상 구조 방식, 행동 기반 방식, 선도 로봇 추종 방식으로 나눌 수 있다. 이 중 선로 로봇 추종 방식은 선도 로봇은 주어진 경로를 이동한다고 가정하고 추종 로봇이 선도 로봇을 추종하도록 하는 것으로 확장성이 용이하여 많은 연구가 이루어 졌다[2,3]. 이러한 연구는 기구학적인 모델만을 고려함으로써 실제 이동 로봇의 질량 및 관성 등의 동적 특성의 변화에 의해 추종 성능에 한계가 있다. 따라서 실제 이동 로봇의 동역학적 모델을 고려한 연구가 진행되었다[4-8]. 일반적인 PID 제어기는 산업 현장에서 많이 사용되고 있으나, 동특성의 변화가 있는 경우 고정된 PID 제어기 이득 값으로는 제어 성능에 한계가 있다.

본 논문에서는 로봇 동역학을 포함한 추종 로봇의 질량이 변화하는 경우의 군집제어(formation control)에 대한 연구로 확장하고자 한다. 추종 로봇의 기구학 제어기를 상위제어기로 구현하고 동역학이 포함된 동적 제어기를 하위제어기로 설정하였다. 하위 제어기에서 추종 로봇의 질량이 변화할 경우, 추종 로봇의 동역학에 의해 적절한 PID 제어기를 선정하기 어렵다. 그러므로 추종 로봇의 고정된 대표적 질량에 대하여 적절한 PID 제어기 이득 값을 전역 탐색 기능이 우수한 유전 알고리즘을 통하여 학습하였다. 이렇게 구한 이득 값과 질량 데이터로 일반화 기능이 뛰어나 불완전한 데이터에 대하여 보간 할 수 있는 신경회로망으로 학습하여 추종 로봇의 질량 변화에 대처하는 제어기를 구현하고자 한다.

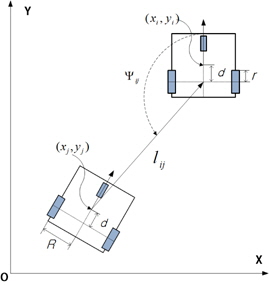
본 논문에서는 그림 1과 같은 선도 로봇(leader robot)과 추종 로봇(follower robot)의 군집제어 모델링을 구성하고 있다.

선도 로봇과 추종 로봇의 위치 관계는 식(1)과 같이 표현된다. 여기서 선도 로봇 자세 (x_i,y_i,θ_i), 추종 로봇 자세 (x_i,y_i,θ_i), 두 로봇 사이의 각도 𝜓_ij, 거리 l_ij이다.

선도 로봇의 선속도 υ_i와 각속도 ω_i가 주어지면 아래의 미분방정식을 통해 선도 로봇의 자세 (x_i,y_i,θ_i)를 구할 수 있다.

이동 로봇의 선속도 υ, 회전 각속도 ω에 대한 관계는 식(3)이 된다.

왼쪽, 오른쪽 바퀴 각각의 각속도(ω_l,ω_r)는 아래 식 (4)과 같다.

여기서 R은 바퀴와 바퀴간의 중심과의 거리이다.

그림 1에 있는 추종 로봇에 대한 비 홀로노믹 (nonholonomic) 이동 로봇의 동역학 방정식은 다음과 같다[7].

여기서 M(q)는 관성행렬, V_m(q,)는 원심력과 코리올리스 행렬, F()는 마찰력, G(q)는 중력, τ_d는 미지의 외란(disturbance)이다. 마찰력, 중력, 외란은 무시 할 수 있는 작은 값이라고 가정한다.

제어기를 설계하기 위한 오차는 식(6)과 같다.

여기서 , 는 목표 거리와 목표 각도이다.

기구학 방정식은 식(7)과 같다[2].

여기서 γ_ij = β_ij + 𝜓_ij = ( θ_i - θ_j ) + 𝜓_ij이다.

위 식(7)을 벡터-행렬 형태로 바꾸면

여기서, , , ,

, .

Input-output feedback linearization을 사용해서 제어량 u_j를 구하면 다음과 같다[2].

로 정의하고 는 목표 값이며 시간 t와 무관한 상수벡터이므로 closed-loop equation은 아래와 같이 쓸 수 있다.

따라서 k₁, k₂가 양의 상수이면 안정함을 알 수 있다.

본 논문에서는 선도 로봇과 추종 로봇의 군집제어로 일정 거리 l_ij와 일정 각도 ψ_ij를 유지하는 것을 목적으로 하고 있다. 군집제어와 관련하여 3.1절의 선도 로봇과 추종 로봇의 기구학적 관계만을 가지고 제어기를 설계할 경우, 실제 군집제어 시 정밀한 제어 성능을 보장 할 수 없다. 이는 추종 로봇이 기구학제어기에 의해 만들어진 식(9)의 선속도와 각속도 u_j = [u_j, w_j]^T를 로봇의 동역학으로 인해 완벽히 추종할 수 없기 때문이다. 따라서 추종 로봇의 동역학을 고려한 제어 시스템을 구성하여야 한다.

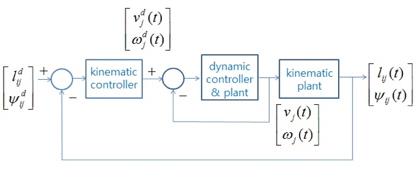
그림 2는 추종 로봇의 동역학을 고려한 전체 제어 시스템의 블록선도를 나타내었다. 제어 시스템은 2개의 제어 시스템을 가지며, 상위 제어기인 기구학제어기와 하위 제어기인 추종 로봇의 동역학을 고려한 동적제어기로 구성하였다[8].

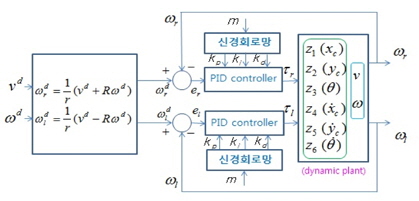
그림 3은 하위 제어기인 추종 로봇의 동역학을 포함한 동역학 제어 시스템을 자세히 나타내었다. 선형 제어기인 PID 제어기는 일정 구간의 동작 범위 내에서 좋은 성능을 보이며, 쉽고 간단하게 동작시킬 수 있으나 부하 및 제어 동작 범위가 변화할 경우, 제어기 이득을 다시 조정하여야 한다.

그러므로 본 연구에서는 추종 로봇의 질량이 임의로 변화할 경우 동적제어기는 신경회로망을 사용하여 PID 제어기의 이득을 조정함으로써 추종 로봇이 선도 로봇을 잘 추종하도록 설계하였다. 신경회로망의 학습을 위해 추종 로봇의 대표적인 질량(10Kg, 20Kg, 30Kg, 40Kg)에 대해 적절한 PID 제어기 이득을 유전알고리즘을 사용하여 학습하였다. 따라서 추종 로봇이 임의의 질량을 갖는 경우, 신경회로망을 통해 보간된 PID 이득을 구해 추종 로봇이 선도 로봇을 효율적으로 추종하도록 하였다. 그림 3에서 상위 제어기에서 나오는 추종 로봇의 목표 선속도 υ_d 와 각속도 ω_d를 추종 로봇의 오른쪽 바퀴의 회전 속도 , 왼쪽 바퀴 회전 속도 로 변환하여 실제 바퀴의 회전 속도 ω_r, ω_l의 오차 값 e_r, e_l을 PID 제어기 입력으로 사용하였다.

이때 추종 로봇의 질량에 따라 신경회로망에서 보간된 K_p, K_i, K_d를 PID 제어기 이득으로 설정한다.

본 논문의 모의실험은 선도 로봇, 추종 로봇 각각 1대씩 구성하였으며 모의실험에 사용한 기구적 변수는 R = 0.5m, r = 0.05m, d = 0.1m이다. 선도 로봇의 초기위치는 (x_i,y_i,θ_i)이고 일정한 선속도 V = 0.5m/s, 각속도 Ω = 0.1rad/s로 하고 추종 로봇은 초기위치 (x_i,y_i,θ_i) = (0, − 1.5,π)로 선정하였다. 선도 로봇과 추종 로봇 사이의 목표 거리 및 각도는 각각 = 0.7m, = 3π/4이다.

추종 로봇의 대표 질량에 따라 적절한 PID 제어기의 이득 값을 구하기 위한 유전알고리즘의 평가함수는 식 (12)과 같이 정의하였다.

여기서, E_L = | - l_ij| 은 상대 거리 오차, E_ψ = | - ψ_ij| 는 상대 각도 오차, t는 시간이며 α, β는 평가 함수의 가중치로 α= 2/3, β = 1/3를 사용하였다. 유전 알고리즘의 학습 조건은 세대수 80, 개체 수 20, 돌연변이 비율 0.2, 교차 비율은 0.6으로 설정하여 PID 제어기의 이득 값을 구하였다.

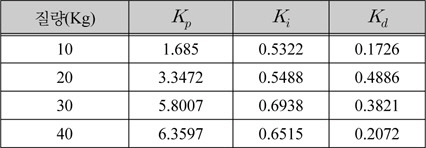
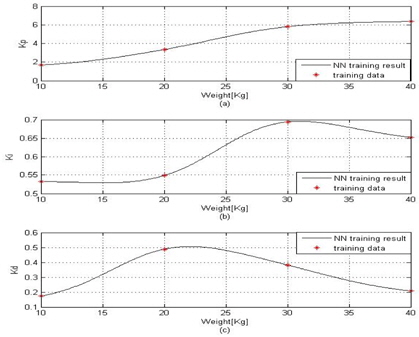
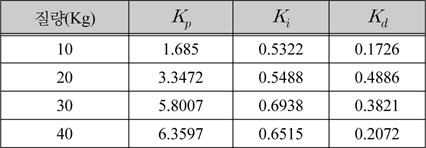
표 1은 추종 로봇의 대표적인 질량에 대해 PID 제어기 이득을 유전 알고리즘으로 구한 값이다. 질량에 따라 PID 제어기의 이득 값이 많이 변화됨을 알 수 있다.

추종 로봇의 질량이 표 1과 같이 유전 알고리즘에 의해 학습되지 않은 임의의 질량에 대해서는 적절한 PID 제어기의 이득을 선정하기 어렵다. 따라서 신경회로망을 통해서 10Kg ~ 40Kg 사이의 모든 질량의 로봇에 대해 적절한 PID 이득 값을 얻고자 한다.

본 논문에서 사용한 신경회로망은 2개의 은닉층(23, 9노드), 1개의 입력과 3개의 출력으로 구성하였다.

그림 4는 표 1의 질량 변화에 따른 PID 제어기의 이득 값을 신경회로망을 사용하여 학습한 결과이다. 추종 로봇의 임의의 질량에 대해서도 적절한 PID 제어기 이득 값을 출력함을 알 수 있다.

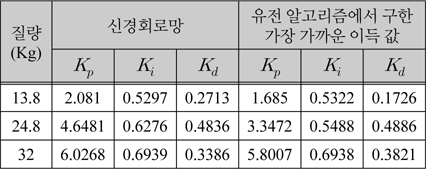
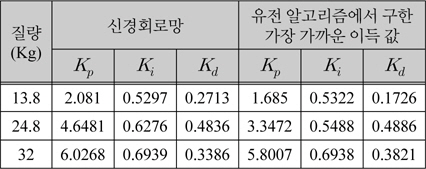
표 2는 추종 로봇의 3가지 임의의 질량에 대해 추종 성능을 비교하기 위하여 학습된 신경 회로망을 사용하여 구한 이득과 유전알고리즘에서 구한 이득 중 가장 가까운 이득 값을 표시하였다. 임의의 질량 13.8Kg, 24.8Kg, 32Kg에서 신경 회로망을 사용한 제어기 이득은 보간된 이득 값을 출력함을 알 수 있다.

비교 실험은 다음의 2가지 경우에 대해 모의실험을 진행하였다. case 1: 신경회로망을 이용한 PID 이득 case 2: 신경회로망을 사용하지 않은 PID 이득

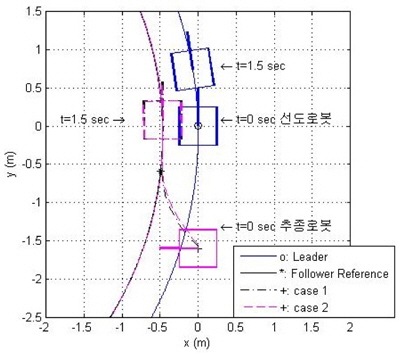
그림 5, 6은 추종 로봇의 질량을 13.8Kg으로 선정하였을 경우, 표 2와 같이 신경 회로망을 이용한 제어기 이득과 유전 알고리즘에서 구한 가장 가까운 이득 값을 사용한 제어 결과이다.

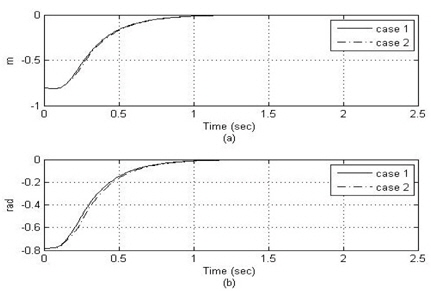
그림 6은 거리 오차와 각도 오차 값으로 신경 회로망을 사용한 제안된 제어방법이 거리 오차와 각도 오차를 감소시키는 것을 확인할 수 있다.

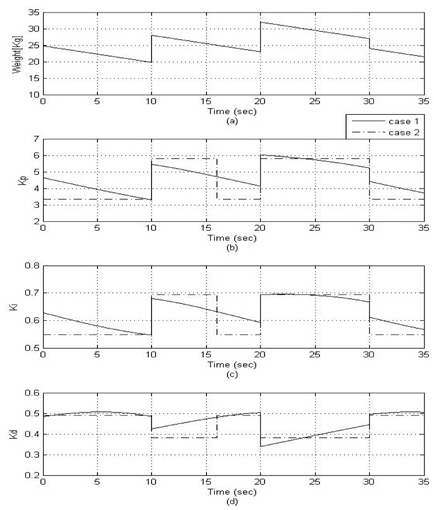
그림 7, 8은 추종 로봇의 질량을 그림 7 (a)와 같이 시간에 따라 1.38kg ~ 32kg으로 변화시킨 경우, 신경 회로망을 사용한 제어기(case 1)와 대표적 질량에 가장 가까운 고정된 이득을 사용한 제어기(case 2)를 비교하였다.

그림 7 (b)~(d)에서 신경회로망을 사용한 제어기는 추종 로봇의 질량 변화에 대하여 매우 능동적으로 PID 이득들이 변화됨을 알 수 있다.

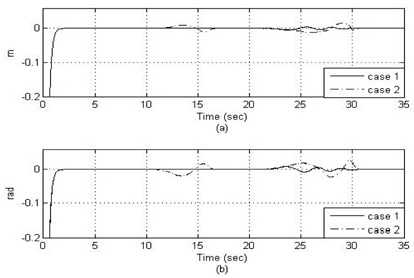
그림 8은 이렇게 변화된 추종 로봇의 질량에 대한 추종 로봇과 선도 로봇 사이의 거리 오차와 각도 오차를 표시하였다. 신경회로망을 사용한 PID 제어 결과가 무게에 따라 고정된 이득을 사용한 PID 제어 결과에 비해 매우 우수한 성능을 나타냄을 알 수 있다. 무게 변화에 대해 PID 이득이 변화되도록 신경회로망을 사용한 제어기가 사용하지 않은 제어기보다 더 안정적으로 주행하며 최종 상태까지 더 빨리 도달하는 것을 알 수 있다.

본 논문은 이동 로봇의 군집제어기에 관한 연구로써 추종 로봇의 질량이 변할 경우, 안정된 제어성능을 갖는 PID제어기를 신경회로망을 이용하여 설계하였다. 추종 로봇의 대표적 질량들에 대해 최적의 PID 이득 값을 유전 알고리즘으로 구하였으며, 대표적 질량들과 최적의 PID 이득 값들을 학습 데이터로 하여 신경회로망 제어기를 학습시켰다. 따라서 추종 로봇의 질량이 임의의 값으로 변화할 경우, 신경회로망을 통해 보간 된 PID 제어 이득 값을 얻도록 하였다. 모의실험 결과를 통해 임의의 질량을 갖는 추종 로봇이 신경회로망을 통해 보간 된 PID 제어기가 그렇지 않은 PID 제어기보다 최종 상태까지 효율적인 움직임을 보이는 것을 알 수 있었으며, 이를 통해 제안된 신경회로망으로 보간 된 이득을 갖는 PID 제어기의 우수성을 검증할 수 있었다.