Currently, with the rapid development of the digital age, multimedia-related image devices become popular. However, images are susceptible to corruption in processing image data due to the impulse noise and active researches have been conducted to restore these images. This paper, in order to restore the damaged images in impulse noise environments, suggested an image restoration algorithm which applies weights depending on spatial distance between directionality and pixel by focusing on damaged pixels. Additionally, this algorithm was compared with existing methods by using the PSNR (peak signal to noise ratio) as the objective standard to judge whether there were improved effects.
최근 산업사회가 고도의 디지털 정보화 시대로 발전함에 따라 영상처리는 여러 분야에 활용되고 있다[1]. 디지털 정보화 시대를 맞이하면서 현대사회는 디지털 장치들의 필요성이 증가되었으며, 영상 관련 기술정보의 공유가 급격히 발전되었다. 그러나 통신기술의 발전에 따라, 영상의 처리, 전송, 저장하는 과정에서 여러 가지 요인에 의해 잡음이 첨가되어 영상이 흐려지게 되어 영상의 질이 저하된다. 이에 따라 영상에 첨가된 잡음의 영향을 완화하기 위해 활발한 연구가 진행되고 있다[2, 3].
영상에 첨가되는 임펄스 잡음을 제거하기 위하여 많은 공간적 기법들이 제안되었으며, 가장 대표적인 잡음제거 기법에는 알파 트림드 평균 필터(A-TMF: alpha-trimmed mean filter)[3], 메디안 필터(SMF: standard median filter)[2,4], 다중 메디안 필터(MMF: multistage median filter)[5], 가중치 필터(WF: weighted filter)[6, 7], 중심 가중치 메디안 필터(CWMF: center weighted median filter)[8], 적응 중심 가중치 메디안 필터(ACWMF: adaptive center weighted median filter) 등이 있다.
본 논문에서는 임펄스 잡음을 효과적으로 제거하기 위하여, 방향성을 고려한 가중치 필터를 제안하였다. 제안한 알고리즘은 임펄스 잡음을 판단한 후, 비 임펄스 잡음일 경우는 원 화소 그대로 보존하고 임펄스 잡음 화소일 경우는 훼손된 화소를 중심으로 방향성과 화소 사이의 공간적 거리에 따라 가중치를 적용하여 처리하였다. 그리고 잡음제거 성능의 우수성을 입증하기 위하여, PSNR을 이용하여 기존의 방법들과 그 성능을 비교하였다.
2.1. SMF(standard median filter)
메디안 필터는 중심 화소와 주변화소를 이용하여, 화소 값을 작은 값부터 큰 값으로 정렬시킨 후, 메디안 값을 선택하여 최종 출렬 화소로 한다[2]. 메디안 필터는 식 (1)과 같이 표현된다.
여기서,
2.2. A-TMF(alpha-trimmed mean filter)
필터링 마스크
여기서
여기서 [·]는 올림 함수를 나타내고,
2.3. CWMF(center weighted median filter)
CWM 필터는 가중치 필터의 한 형태로서 중심 화소에 대해서만 2
여기서,
본 논문에서 제안한 알고리즘은 잡음 판단과 잡음제거 부분으로 나눈다. 임펄스 잡음 판단을 거쳐, 비 잡음 화소일 경우는 원 화소 그대로 출력하고, 잡음 화소일 경우 방향성을 고려하여 각 방향 화소에 가중치를 설정하여 처리한다.
임펄스 잡음에 의하여 훼손된 영상은 다음 식 (5)와 같이 표현된다[7].
여기서
본 논문에서는 임펄스 잡음을 제거하는데 임펄스 잡 음 신호의 화소값은
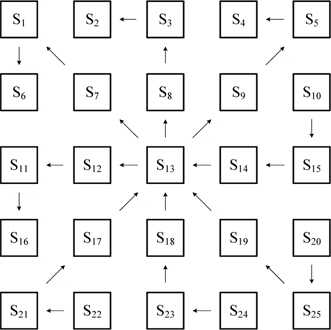
잡음 판단 과정을 거친 후, 잡음 신호에 대해서는 그림 1과 같은 필터링 마스크와 같이 4개의 방향으로 선정하여 처리한다.
Step 1. 화소
Step 2. 잡음화소 검출에 의해 각 방향 벡터를 2진화 형태로 나타낼 경우, 식 (7)과 같이 표현된다.
여기서
Step 3. 각 방향에서 중심 화소와의 공간적 거리에 의하여 각 방향벡터에 가중치
여기서
Step 4. 세분화한 부분 집합 과 2 진화 의 곱에 가중치를
Step 5. 각 방향에서 비 잡음 화소의 개수를
Step 6. 각 방향에서 비 잡음 화소수가 가장 큰 두 방향의 출력값
여기서 가중치
Step 7. 따라서 최종 출력 화소값은 식 (11)과 같이 나타낸다.
여기서
본 논문에서는 임펄스 잡음을 효과적으로 제거하기 위하여, 방향성을 고려한 가중치 필터를 제안하였으며, 8 비트 그레이 영상 Lena와 Camera man(512×512)에 임펄스 잡음 10%~60%를 첨가하여 시뮬레이션하였다. 또한 영상 잡음제거 성능의 우수성을 입증하기 위하여 PSNR을 사용하여 기존의 SMF, A-TMF, CWMF 방법들과 성능을 비교하였으며, 그 기준으로 PSNR을 사용하였다.
그림 2는 Lena 영상과 Camera man 영상에 잡음 밀도가 40%인 임펄스 잡음을 첨가하였을 경우의 영상이고, 그림 3은 제안한 방법과 기존 방법들의 시뮬레이션한 결과이다.
그림 3에서 (a)는 메디안 필터(SMF), (b)는 알파 트림드 평균 필터(A-TMF)(α = 0.1), (c)는 중심 가중치 메디안 필터(CWMF)(5×5), (d)는 제안한 필터 알고리즘(PFA: proposed filter algorithm)으로 처리한 결과이다.
시뮬레이션 결과, 메디안 필터로 처리한 영상은 잡음밀도가 높은 영역에서 잡음제거 특성이 미흡하고,알파트림드 평균 필터로 처리한 영상은 잡음을 제거함에 있어서 블러링 현상이 일어났으며, 중심 가중치 메디안 필터는 메디안 필터의 변형으로서 마스크의 크기를 변화시킴에 있어서 우수한 결과를 나타내었다. 그러나 마스크 내의 메디안 값이 잡음일 경우 특성이 미흡하여 일부 잡음이 제거되지 않았다. 그러나 제안한 알고리즘으로 처리한 결과는 잡음 밀도가 낮은 영역에서도 우수한 특성을 나타내었으며, 높은 영역에서도 우수한 잡음 제거특성을 나타내었다.
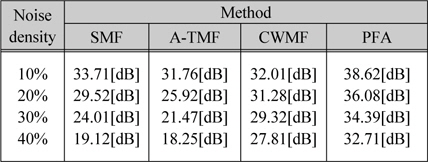
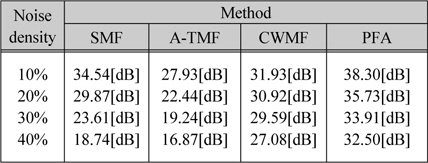
그림 4는 각 필터의 PSNR을 나타낸 것이며, Lena와 Camera man 영상의 PSNR 수치를 표 1과 2에 각각 나타내었다. 표 1의 Lena 영상 결과에서 잡음 밀도가 40%인 경우, 32.71[dB]의 높은 PSNR을 보이고 있고, 기존의 SMF, A-TMF, CWMF에 비해 각각 13.59[dB], 14.46[dB], 4.90[dB] 개선되었으며, 표 2의 Camera man 영상 결과에서 13.76[dB], 15.63 [dB], 5.42[dB] 개선되었다.
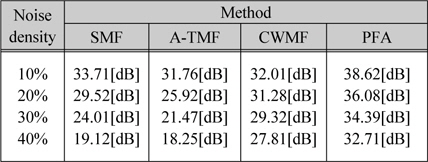
각 방법의 PSNR(Lena 영상)
[표 2.] 각 방법의 PSNR(Camera man 영상)
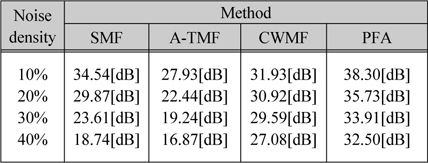
각 방법의 PSNR(Camera man 영상)
본 논문은 임펄스 잡음환경에서 훼손된 영상을 복원하기 위하여, 방향성을 고려한 가중치 필터를 제안하였다. 제안한 알고리즘은 임펄스 잡음을 판단한 후, 비 잡음일 경우는 원 화소 그대로 보존하고 잡음 화소일 경우는 방향성을 고려하여 화소 사이의 공간적 거리에 따라 가중치를 적용하여 처리하였다. 시뮬레이션결과, 기존의 방법들에 비해 제안한 알고리즘은 잡음 밀도가 높은 영역 및 낮은 영역에서도 우수한 PSNR 결과를 나타내었다. 따라서 제안한 알고리즘은 다양한 영상처리 분야에 유용하게 사용되리라 사료된다.