통신채널의 인식문제는 현재 이론적 부분과 실제 관점 부분의 문제점을 가지고 있다. 최근에 이 문제를 해결키 위해 제안된 기법들은 안테나 구조와 시간 오버샘플링에 의해 유도된 다이버시티를 이용하고 있다. 이 방법은 선형 제한조건을 가진 적응필터를 이용하고 있다. 본 논문에서는 값 분할에 근거한 기법이 제안되었다. 수신신호 상관행렬의 최소 단일값에 의한 단일벡터는 채널 임펄스 응답을 포함하며 상기 문제를 해결키 위한 적응 알고리즘을 보인다. 제안된 기법은 기존 기법의 성능보다 우수함을 알 수 있다.
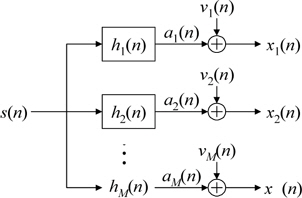
In HOS-based methods, because the performance index as the optimization criterion is nonlinear with respect to estimation parameters and these methods require a large amount of data samples. These methods have the disadvantage that their computational complexity may be large. See, for example, [1] and references therein. Since the seminal work by Tong et al. the problem of estimating the channel response of multiple FIR channel driven by an unknown input symbol has interested many researchers in signal processing and communication fields. This is achieved by exploiting assumed cyclostationary properties, induced by oversampling or antenna array at the receiver part[1,2]. The basic blind channel identification problem involves a channel model where only the observation signal is available for processing in the identification channel. Earlier blind channel identification approaches mostly depend on higher order statistics (HOS), because the second order statistics (SOS) does not contain phase information for stationary signal[3-4]. Most communication channels are time-varying in practice. Therefore, the algorithms should be able to track the change of the channel impulse response. Moreover, in a fast fading channel, the multipath channels in wireless communications vary rapidly, and we only have a few data samples corresponding to the same channel characteristics. Blind channel identification technique has been developed in adaptive algorithm based on vector-correlation method [8,9,11]. But most algorithms neglected the effect of channel noise.
Most notations are standard: vectors and matrices are boldface small and capital letters, respectively; the matrix transpose, the complex conjugate, the Hermitian, and convolution are denoted by (·)T, (·)*, (·)H and ⊗, respectively;
This paper is organized as follows. In section II, we review the basic assumption and identification issues. And the existing adaptive algorithms of the block LS methods are described also. A novel blind channel identification technique based on eigenvlaue decomposition and adaptive implementation are proposed in section III. Simulation results with real measured channel are performed in section IV. Section V concludes our results.
Ⅱ. Basic Assumption and Issues
In this paper, consider a special case, when the channel output is two times oversampled or there are two antennas at the receiver, this is equivalent to two channel representation (
Then
Let 𝒳(
where
where
The blind identification problem can be stated as follows: Given the observation of channel output {
A1) Subchannels do not share common zeros, or in other words, they are coprime.A2) The noise v(n) is zero mean, white with known covariance, no cochannel correlation, and uncorrelated with source signal.A3) The channel has known order L.
The assumption that
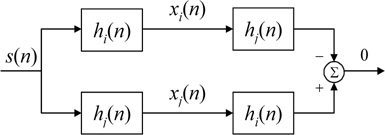
As described in [5], to avoid the trivial solution to minimization problem a proper condition must be selected. In this section, a new approach is proposed that is based on eigenvalue decomposition. Indeed, the eigenvector corresponding to the minimum eigenvalue of the covariance matrix of the received signals contains the channel impulse response. This approach is based on the unit norm constraint that is apart from the linear constraint introduced in the previous section[6].
>
A. Concept of the Proposed Scheme
Number equations consecutively with equation numbers in parentheses flush with the right margin, as in (1). We assume that the channel is linear and time invariant within small time interval; therefore, we have the following relation as described in (4)
where
and the channel impulse response vector of length
The covariance matrix of the two received signals is given by
Consider the 2L´1 vector as follows:
From (5) and (8), it can be seen that Rxh=0, which means that the vector h is the eigenvector of the covariance matrix Rx corresponding to the eigenvalue 0.
Moreover, if the two channel impulse response h1 and h2 have no common zeros and the autocorrelation matrix of the source signal
where x(
If the correlation matrix of the vector x(
We note from (11) that h is the eigenvector of the correlation matrix Rx and is the corresponding eigenvector of Rx. The knowledge of can be obtained as a by product if wanted.
In practice, it is simple to estimate iteratively the eigenvector corresponding to the minimum eigenvalue of Rx, by using an algorithm similar to the Frost algorithm that is a simple constrained LMS algorithm [7].
Minimizing the quantity h
Let us define the error signal
where x(
and we obtain the gradient-descent constrained LMS algorithm:
where
and taking statistical expectation after convergence, we get
which is what is desired: the eigenvector h(∞) corresponding to the smallest eigenvalue
In practice, it is advantageous to use the following adaptation scheme
The algorithm (18) presented above is very general to find the eigenvector corresponding to the smallest eigenvalue of any matrix Rx. If the smallest eigenvalue is equal to zero, which is the case here, the algorithm can be simplified as follows:
and
Computer simulations were conducted to evaluate the performance of the proposed algorithm in comparison with existing algorithms. In all the simulations, two channel SIMO model is assumed. This means two times oversampling or two sensors at the receiver in real situation. The input signal is 4-QAM. For simplicity of comparison, we assumed that the channel order
where
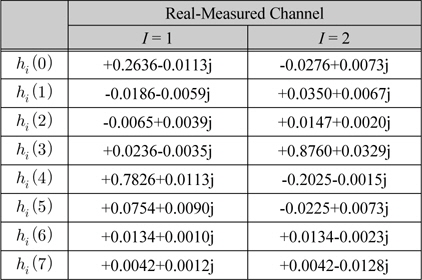
We used real-measured microwave channel. The shortened length-16 version of an empirically measured
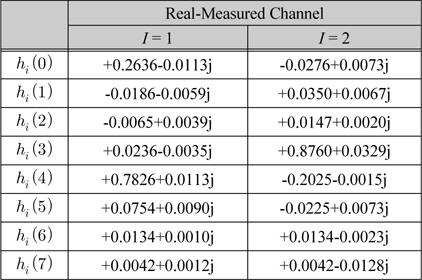
채널 계수
The shortened version is derived by linear decimation of the FFT of the full-length
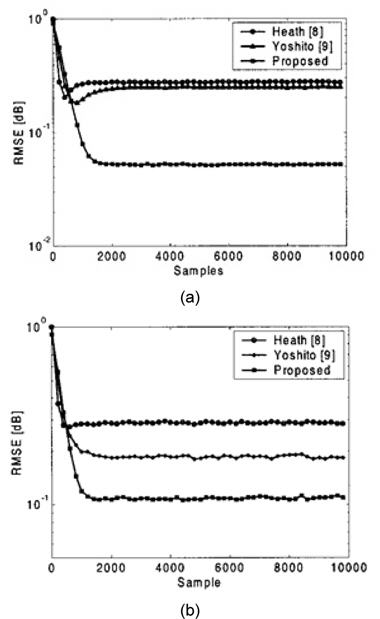
Fig. 3 shows the RMSE of the channel estimates from existing algorithms and the proposed algorithm. From these figures, we can see that the proposed algorithm always performs better than others. By inspection, we can observe that RMSE values of the proposed method are decreased more or less 6-10 dB, and 1-2 dB under 20 dB, and 10 dB, respectively. Clearly, we can observe the significant improvement of the proposed algorithm over existing algorithms.
In this paper, an approach to channel identification has been presented. The method is based on eigenvalue decomposition. The eigenvector corresponding to the minimum eigenvalue of the covariance matrix of the received signals contains the channel impulse response. And we use a simple constrained LMS algorithm to estimate iteratively the eigenvector corresponding to the minimum eigenvalue. In comparison with algorithms, the proposed one seems to be more efficient in a low SNR channel and much more accurate.