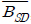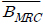The conventional best relay selection based on all the channel information for the first and second hops in dual-hop systems has a large consumption of resources for channel feedback. In this paper, we analyze the average bit error rate for partial relay selection based on the channel information only for the first hop in dual-hop decode-and-forward relaying systems, where we assume independent Rayleigh fading channels. In particular, we provide an exact and closed-form expression for the average bit error rate of
공간 다이버시티(diversity)는 송수신기에 여러 개의 안테나를 설치하여 다중의 통신 경로를 생성하는 기법이다. 이 기법에는 공간의 제약이 있는 모바일노드에 적용하기 힘들다는 단점이 있다. 이에 따라, 소스 노드와 목적지 노드 간 중계 노드가 모바일 노드의 역할을 대신 하는 협력 다이버시티 시스템이 제안되어 왔다 [1-3]. 이 시스템은 중계 노드들의 안테나들과 시간, 주파수 자원을 공유함으로서 가상의 안테나 배열을 생성하여 다이버시티 이득을 얻는다. 협력 다이버시티 시스템의 대표적인 중계 시스템으로는, 증폭 후 전달 중계 시스템(Amplify-and-Forward, AF)과 디코딩 후 전달 중계 시스템(Decode-and-Forward, DF)이 있다[4].
협력 다이버시티 시스템에서 중계 노드 수의 증가는 스펙트럼 효율의 손실을 가져온다[5]. 이것은, 소스 노드와 중계 노드 간 간섭을 줄이기 위하여 항상 수신 신호들의 직교성이 유지되어야 하기 때문이다. 즉, 중계 노드의 개수만큼 자원의 할당이 요구된다. 이와 같은 비효율적인 자원의 소모를 줄이기 위해, 가장 좋은 종단 간 수신 신호 대 잡음비(Signal-to-Noise Ratio, SNR)를 제공하는 하나의 중계 노드를 선택하는 기법(Best Relay Selection, BRS)이 제안되었다[6]. [6]에서는 첫 번째 홉과 두 번째 홉에 대한 채널 정보를 모두 이용하기 때문에 큰 피드백 오버헤드(feedback overhead)를 요구한다. [7]에서는 [6]에서의 단점을 보완하기 위하여 첫 번째 홉의 채널 정보만을 이용하는 부분 중계 노드 선택 기법(Partial Relay Selection, PRS)을 제안하였다. 두 홉의 채널 정보를 모두 필요로 하는 BRS기법에 비하여 한 홉의 채널 정보만을 필요로 하는 PRS기법은 피드백 오버헤드 및 전력 소비의 측면에서 이점을 나타낸다. [8]에서는, 듀얼 홉 AF 중계 시스템에서의 레일레이 페이딩 채널을 가정하여 BRS기법에 대한 점근적인 심볼 오차율 표현식을 유도하였다. 이 때, 기존의 협력적 중계 노드 선택 기법과의 비교를 통해 다이버시티 이득과 성능을 분석하였다. [9]에서는, 듀얼 홉 AF 중계 시스템에서 PRS기법에 대한 성능을 평가하기 위해, 레일 레이 페이딩 채널을 가정하여 비트 오차율과 아웃티지 확률에 대한 정확한 표현식을 유도하였다. [10]에서는, 듀얼 홉 네트워크에서 레일레이 페이딩 채널을 가정하여 PRS기법을 이용하는 DF 중계 시스템에서 높은 SNR에 대한 아웃티지 확률과 심볼 오차율의 근사 표현식을 유도하였다.
지금까지, PRS기법을 이용하는 듀얼 홉 DF 중계 시스템에서 정확한 비트 오차율 성능에 대한 연구는 진행되지 않았다. 특히, [11]에서 처럼 DF 중계 노드에서 디코딩의 성공 여부를 실제와 유사하게 비트 오차를 토대로 판단하여, PRS기법에 대한 비트 오차율 성능을 연구한 사례는 없다.
본 논문에서는, [11]과 같이 중계 노드에서 디코딩의 성공 여부를 비트 오차를 토대로 판단하는 디코딩 후 전달 중계 시스템을 고려하여, 독립적이고 균일한 분포를 따르는 채널에서 PRS기법에 대한 평균 비트 오차율의 정확한 표현식을 유도한다. 이 때, QAM(Quadrature Amplitude Modulation)의 변조방식을 이용한다. 또한, 소스 노드와 목적지 노드 간 직접 경로를 고려하여, 목적지 노드에서 중계되어 수신된 신호와 직접 수신된 신호를 결합하기 위하여 최대 비율 결합(Maximal Ratio Combining, MRC)[12]을 이용한다. 최종적으로, 수치적 결과를 통해 모든 분석적인 표현식을 검증하고, 중계 노드의 수, 그리고 첫 번째 홉과 두 번째 홉의 평균 채널 전력비를 다양하게 가정하여 PRS기법과 BRS기법의 비트 오차율 성능을 비교한다.
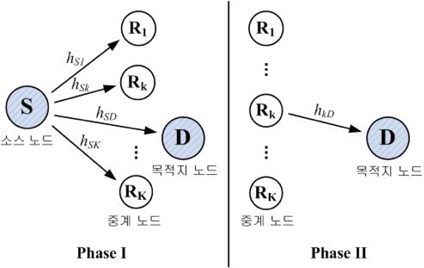
본 논문에서는 하나의 소스 노드(
그림 1에서와 같이, 소스 노드와
Phase I에서, 소스 노드는 하나의 시간슬롯 동안 송신 심볼을 목적지 노드와
이 때, 선택된 중계 노드에서 디코딩이 성공한 경우에만 심볼의 전송이 이뤄지며, 전송되는 심볼은 소스 노드에서와 동일한 변조 방식으로 변조된 것이다. 목적지 노드에서 최종적으로 수신된 신호들은 최대 비율 결합을 이용하여 결합한다.
본 논문에서는 플랫(flat) 레일레이 페이딩 채널을 가정하여, 모든 채널이 독립적이고 균일한 분포를 따른다고 가정한다. 따라서, 모든 중계 노드(
III. M -ary QAM 변조에 대한 비트 오차율 분석
듀얼 홉 DF 중계 시스템에서 레일레이 페이딩 채널을 가정하여 PRS기법을 이용한 종단 간 평균 비트 오차율은 다음과 같이 표현된다.
식 (5)에서, 는 k번째 중계 노드가 K개의 중계 노드 중 가장 큰 수신 SNR을 제공할 때,
여기서, , 는 각각 소스 노드와 목적지 노드 간 직접적인 링크에 의해 수신된 심볼의 비트 에러 확률, 소스 노드와 목적지 노드 간 직접적인 링크와 선택된 중계 노드와 목적지 노드 간 링크에서 수신된 심볼들의 MRC 결합에 대한 비트 에러 확률을 의미한다. , 는 각각 선택된 중계 노드에서의 디코딩 실패 확률과 성공 확률을 의미하고, 다음과 같이 표현된다.
식 (7)에서, 는 선택된 중계 노드에서 수신된 QAM 변조 심볼의 에러 확률을 의미한다. 이것은 선택된 중계 노드에서의 디코딩 실패 확률과 성공 확률을 얻을 때 이용되고, 다음과 같이 표현된다.
식 (8)에서, 는 선택된 중계 노드에서 수신된 심볼의 비트 에러 확률을 의미한다.
[11]의 식 (6)을 이용하여, 레일레이 페이딩 채널을 가정한
여기서,
이고,
여기서,
이다.
최종적으로, [11]의 식 (8)에서
3.1. 직접적인 링크에 의해 수신된 심볼의 비트 에러 확률,
직접적인 링크에 의해 목적지 노드에서 수신된 심볼의 비트 에러 확률은, 식 (9)에서
3.2. 직접적인 링크와 중계 링크에 의해 수신된 심볼의 MRC-출력 비트 에러 확률,
식 (12)을 이용하여, 목적지 노드에서
식 (13)에서, [13]의 식 (5A.58-60)을 이용하여 다음과 같은 표현식을 얻는다.
식 (10)과 동일한 방식으로, 목적지 노드에서의
3.3. 선택된 중계 노드에서 수신된 심볼의 비트 에러 확률 , Bk*
그러나
누적 분포 함수의 미분을 통해,
이제, 식 (16)은 다음과 같이 표현될 수 있다. 전개 시, 이항정리(binomial theorem)를 이용한다.
식 (19)을 이용하여, 선택된 중계 노드에서
식 (20)에서, [13]의 식 (5A.9)를 이용하여 다음과 같은 표현식을 얻는다.
여기서,
이다.
식 (10)과 동일한 방식으로, 선택된 중계 노드에서 수신된
최종적으로, 얻어진 식 (22)을 식 (8)에 대입한다. 그리고 식 (8)을 식 (7)에 대입한다. 식 (7)을 3.1절, 3.2절에서 각각 유도된 식 (11), 식 (15)과 함께 식 (6)에 대입하여 PRS기법 기반의 QAM 변조 심볼에 대한 평균 종단 간 비트 오차율을 구할 수 있다.
본 장에서는 III장에서 유도한 비트 오차율 수식들과 몬테카를로(Monte Carlo) 시뮬레이션 결과를 비교하여 정확한 수식 분석이 이뤄졌는지 확인하고, 그 확인된 식들을 이용하여 듀얼 홉 DF 중계 시스템에서의 PRS기법을 이용한 종단 간 비트 오차율과 BRS기법을 이용한 종단 간 비트 오차율의 성능을 비교한다.
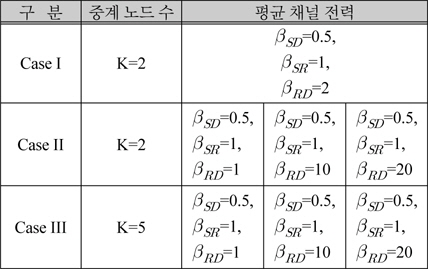
시뮬레이션은 표 1과 같은 세 가지 경우를 고려한다. 표 1의 모든 경우에서 소스 노드와 목적지 노드 간 직접적인 링크의 평균 채널 전력은 0.5로 가정한다. Case I 에서, 중계노드 수
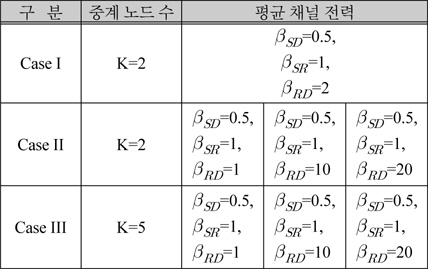
시뮬레이션 시나리오
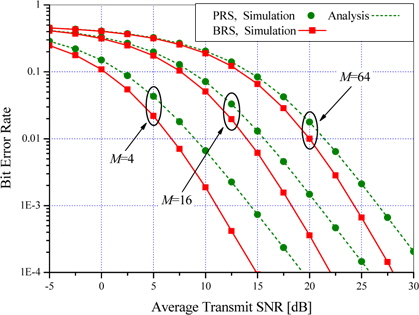
그림 2는 Case I에 대한
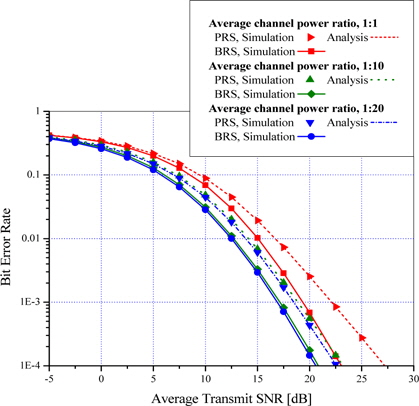
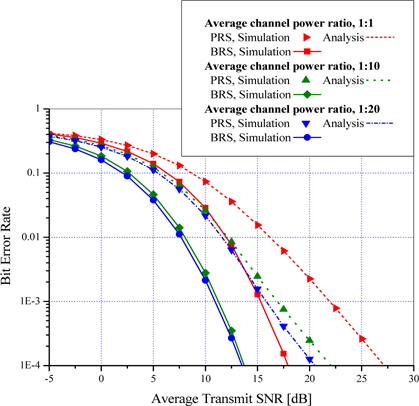
그림 3과 4는 각각 Case II, Case III에 대한 16-ary QAM의 평균 비트 오차율을 나타낸다. 여기서, PRS기법을 이용하여 유도된 수식과 시뮬레이션 결과가 완벽히 일치함을 볼 수 있다. 두 그림에서
그림 3, 4에서 낮은 SNR에서의 PRS기법은, 두 홉 간 평균 채널 전력비에 따라 거의 영향을 받지 않거나
그러나 높은 SNR에서는
본 논문에서는 독립적이고 균일한 분포를 갖는 채널을 가정하여 듀얼 홉 DF 중계 시스템에서 PRS기법을 이용하여 정확한 비트 오차율을 분석하였다. 특히, IV장에서 중계 노드의 수와 첫 번째 홉과 두 번째 홉 간 평균 채널 전력비를 다양하게 가정하여 PRS, BRS기법의 평균 비트 오차율을 분석하였다. 분석 결과를 통해, 높은 SNR 에서 PRS기법은 첫 번째 홉의 평균 채널 전력이 두 번째 홉의 평균 채널 전력보다 작을수록 BRS기법에 근접하여, 큰 이득을 보인다는 것을 알았다. 그리고 첫 번째 홉과 두 번째 홉 간 비율이 1:10이상으로 증가함에 따라 제안된 시스템의 이득이 미미해지는 양상을 나타내어, 일정한 지점에서 이득치의 포화가 발생함을 알 수 있다.
또한, PRS기법은 중계 노드의 수가 증가함에 따라 평균 비트 오차율의 성능 개선이 미미하다는 결론을 얻었다.