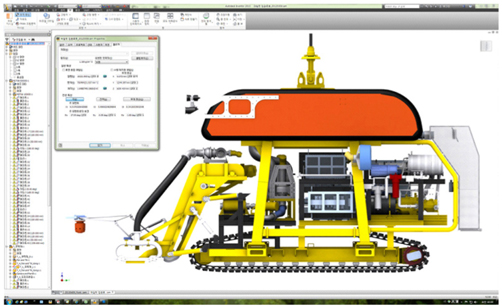
심해저 광물자원 개발을 위하여 선박해양플랜트연구소에서는 자항식 시험집광기를 개발하였고 실해역 실험을 성공적으로 수행하였다(Hong et al., 2008; Hong et al., 2009). 또한 2012년도에는 기존의 2열 무한궤도에서 채집의 효율을 증대하기 위하여 Fig. 1과 같이 4열 무한궤도 형태로 이루어진 “미내로(MineRo)”를 설계 개발하였다(Hong et al., 2013).
개발단계에 있어 접지 길이, 궤도 간격 등 다양한 해석 조건을 바탕으로 미내로의 선회 주행 시뮬레이션을 수행하고, 결과를 설계에 반영하였다.(Kim et al., 2013) 또한 4열 무한궤도 차량이 선회 주행할 때 입력 속도, 선회비 등의 속도프로파일에 따라 어떠한 특성을 보이는지도 해석을 통해 확인한 바 있다.(Lee et al., 2009) 심해저 채광 로봇의 주행 해석에 있어서 가장 중요한 요소는 궤도와 지반과의 상호작용관계이다. 선박해양플랜트연구소에서는 심해저 지반의 모사지형을 만들고 수치해석을 위한 토양모델에 필요한 토양의 전단강도 및 기타 계수를 측정하기 위한 노력을 수행하여왔다(Hong and Choi, 2001). 이러한 실험은 장비가 크기 때문에 필요한 토양 샘플의 양이 많이 필요하다. 하지만, 실제 실험지역의 토양 샘플을 원하는 양만큼 얻기가 쉽지 않고, 또한 작은 양의 샘플을 이용하여 측정할 수 있는 토양모델 계수의 수가 한정되어 있기 때문에 실험을 수행하여 정확한 토양모델 계수를 얻기란 쉽지 않은 일이다. 그렇기에 실제 실험환경에서의 결과를 예측하는데 어려움이 있다.
본 논문에서는 기 설계된 미내로의 입력 속도 및 선회비를 입력하고, 다양한 토양모델 계수에 따른 주행성능을 분석하고자 한다. 이때 고려해야 할 변수의 개수가 많고, 또한 변수의 값의 구간이 많을 경우 해석해야 하는 경우의 수가 많아져 많은 시간이 소요된다. 그렇기 때문에 본 논문에서는 적은 해석을 통해 전체의 경향을 분석할 수 있는 직교 배열표를 활용하고자 한다. 이를 토대로 실제 실험지역에서의 토양모델 계수 값을 예측하고, 실해역에서 미내로의 주행특성을 예측하고자 한다.
수치해석을 위한 미내로의 제원은 Table 1에 나타나 있다. 이러한 값은 Fig. 2에서와 같이 3차원 CAD(Computer aided design) 모델에서부터 측정을 하였으며, 실제 무게측정을 통하여 확인을 하였다.
[Table 1] Specifications of MineRo model

Specifications of MineRo model
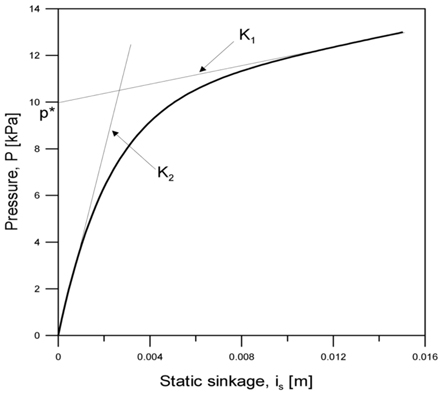
궤도와 지반과의 상호작용에 의한 힘을 나타내는 토양모델은 크게 수직응력과 전단응력으로 나눌 수 있다. 수직응력은 식 (1)과 같이 압력-침하간의 관계식으로 표현된다.
여기서
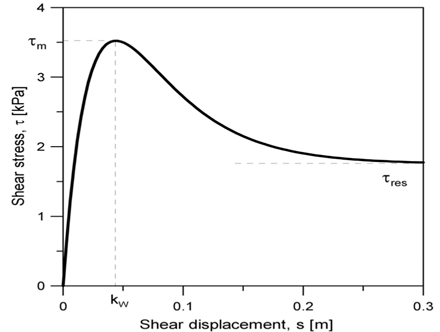
전단응력은 식 (2)와 같이 전단변위-전단응력의 관계식으로 표현된다(Wong, 1993).
여기서,
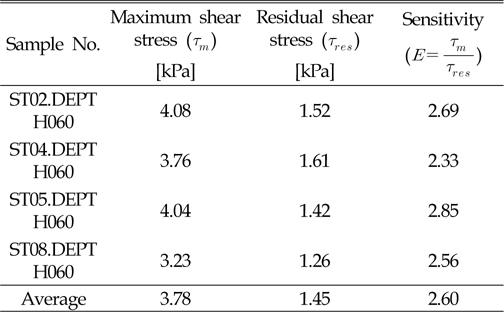
식 (2)의 토양모델의 최대 전단강도 및 민감도를 구하기 위하여 다음의 Fig. 5에서와 같이 전단강도 계측장치를 이용하여 전단응력을 측정하였다. 실험에 사용된 토양은 실해역 실험 지역에서 중력코어를 통해 획득하였다. Fig. 5와 같이 토양샘플 표면으로부터 6 cm 깊이에서 전단강도를 측정 하였으며, 그 결과는 Table 2에 나타내었다.
[Table 2] Shear stress of inshore test site
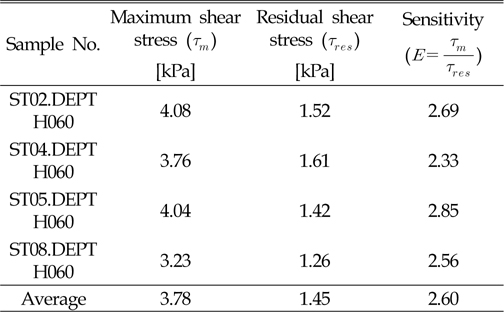
Shear stress of inshore test site
이와 같은 실험을 통하여 토양의 최대 전단응력 및 민감도를 측정할 수 있었다. 하지만 이러한 정보는 토양모델의 일부 값에 지나지 않기 때문에 토양의 수직 응력 및 기울기 등 나머지 변수 값을 변화시켜가면서, 변수에 따른 미내로의 주행성능을 분석하여야 한다.
미내로의 선회 주행을 위하여 다음과 같은 변수 및 값을 선정하였다.
∎ 선회 기준 속도(Vref) [m/s] : 0.2, 0.3, 0.4, 0.5, 0.6 ∎ 선회비 : 1.1, 1.3, 1.5, 1.7, 1.9 ∎ 최대전단응력(τm) [kPa] : 3, 3.5, 4, 4.5, 5 ∎ 민감도(E) : 2, 2.25, 2.5, 2.75, 3 ∎ 최대전단응력 시 전단변위(kw) [m] : 0.04, 0.1, 0.2, 0.4, 0.6 ∎ 토양의 수직 응력(p0) [kPa] : 11, 13, 15, 17, 19 ∎ 토양모델 계수(K1) : 10, 15, 20, 25, 30 ∎ 토양모델 계수(K2) : 370, 420, 470, 520, 570
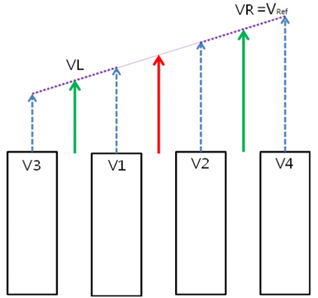
여기서, 최대전단응력 및 민감도는 실해역 실험을 통해 측정된 값을 포함하는 범위로 입력 값을 선정하였다. 선회 기준 속도는 선회 시 바깥쪽 궤도의 평균 속도를 나타내며, 선회비는 좌측 궤도와 우측 궤도의 속도 평균의 비를 나타낸다.
1,000초의 주행 시뮬레이션을 적분간격 10ms로 수행하였을 경우 한 번의 수치해석에 소요되는 시간은 대략 4분 30초이다. 이는 Intel i7 3.5GHz의 성능을 갖는 CPU를 사용하였을 경우의 해석 소요시간이다. 위와 같이 8변수 5수준의 해석을 수행하기 위해서는 총 390,625개의 해석을 수행하여야 한다. 이는 동일 CPU 12개로 나누어 해석을 하여도 대략 100일의 시간이 걸리는 양이다. 그렇기 때문에 본 논문에서는 최적설계기법의 민감도 분석에서 사용되는 직교배열표(Park and Kang, 2007)를 이용하여 총 1840가지의 해석 경우의 수가 도출되었으며, 이를 통해 미내로의 선회 특성을 파악할 수 있도록 하였다.
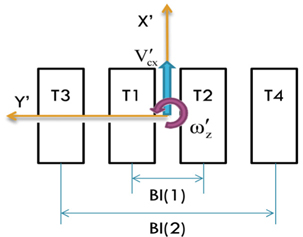
미내로의 선회 주행 특성을 분석하기 위하여, 응답특성으로 선회반경, 침하량, 궤도의 슬립율을 선정하였다. 궤도의 슬립율은 Fig. 7에서와 같이 각 궤도 중심에서의 속도와 각 궤도의 입력속도를 이용하여 다음의 식 (6)에서와 같이 계산하였다.
여기서
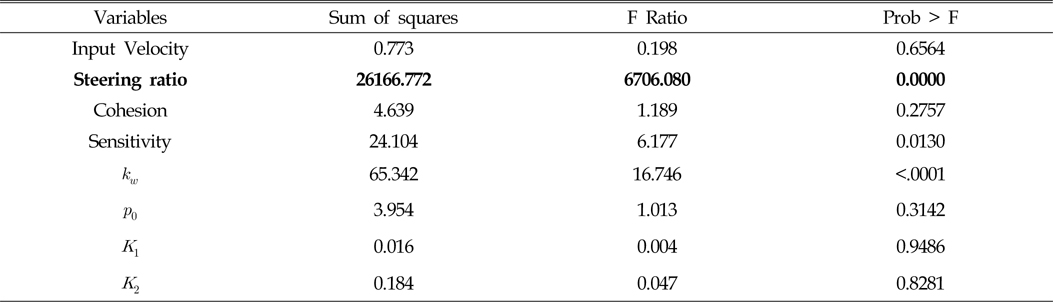
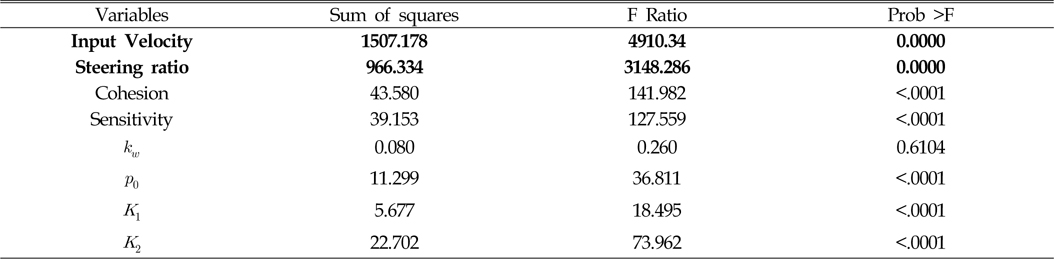
Table 4는 각 요소에 따른 선회반경의 영향도를 분석한 표이다. 이 표에서 보듯이 F ratio가 가장 큰 선회비가 선회반경에 가장 큰 영향을 보임을 확인할 수 있다. 보다 효과적인 분석을 위하여 Fig. 8에 각 요소에 따른 선회반경의 분포도를 나타내었다. 굵은선으로 표시된 선회비 그래프에서 보듯이 선회비가 선회반경에 가장 큰 영향을 보임을 확인할 수 있으며, 선회비가 증가할수록 선회반경이 작아지는 경향을 확인할 수 있다.
[Table 4] Analysis of effect for turning radius of MineRo with respect to input variables
Analysis of effect for turning radius of MineRo with respect to input variables
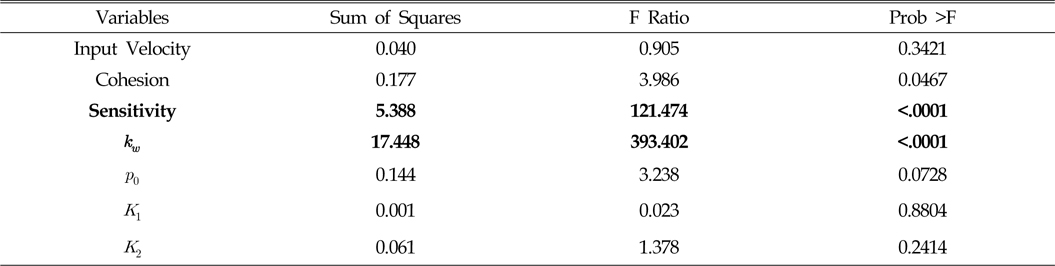
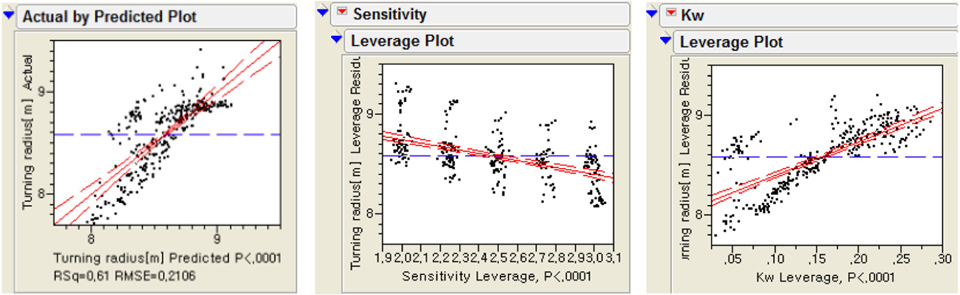
이와 같이 선회반경에는 선회비가 가장 중요함을 확인하였다. 선회비는 사용자가 설정 가능한 변수이며, 사용자가 설정할 수 없는 토양계수의 영향도를 자세히 분석하기 위하여 선회비를 고정하였을 경우에 대한 민감도 분석이 필요하다. 그래서 선회비를 1.4로 고정하였을 경우의 결과만을 추출하여 민감도 분석을 수행하였다. 그 결과 Table 5와 Fig. 9에서와 같이 토양의 민감도와 최대전단강도에서의 전단변위인
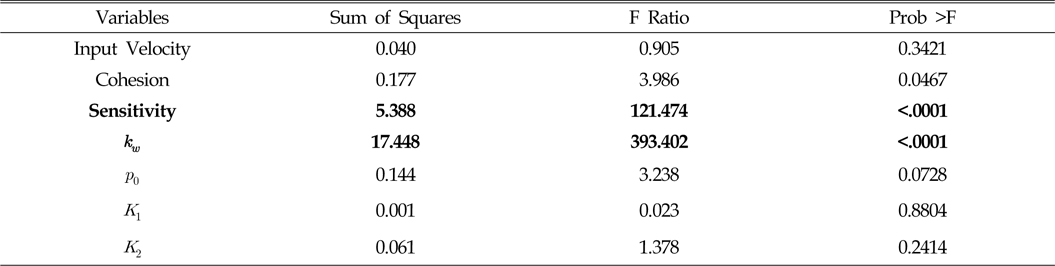
Analysis of effect for turning radius of MineRo with respect to input variables (Steering ratio = 1.4)
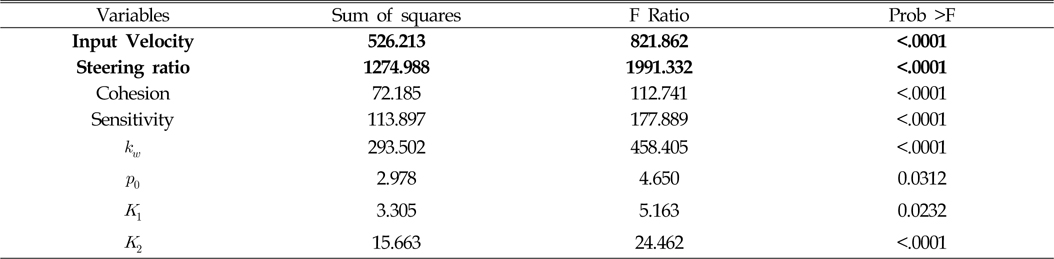
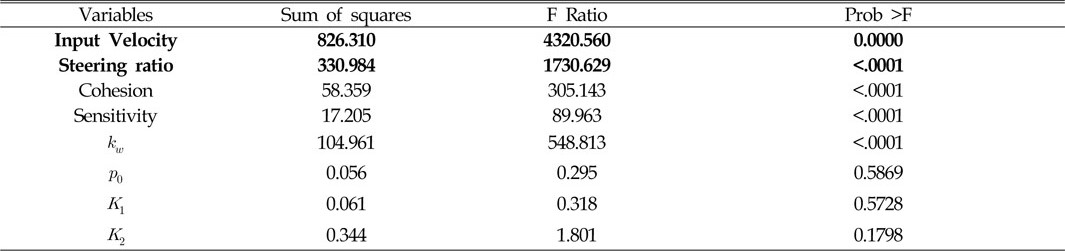
다음의 Table 6과 Fig. 10은 각 요소에 따른 침하량의 영향도 및 그래프를 나타낸 것이다. Fig. 10에서 굵은선 박스는 가장 영향이 큰 것을 표시한 것이며, 점선 박스는 주요한 영향을 미치는 인자에 대한 그래프를 나타낸 것이다. 이 결과에서 보듯이 침하량 역시 선회반경의 영향을 가장 크게 받는 것을 확인할 수 있으며, 선회비가 증가할수록 침하량도 증가하는 경향을 보인다. 또한 침하량의 경우 모든 입력변수의 영향을 받지만 특히 압력-침하에 대한 토양의 입력 값에 영향을 받음을 확인할 수 있다. Fig. 10에서와 같이
[Table 6] Analysis of effect for sinkage of MineRo with respect to input variables
Analysis of effect for sinkage of MineRo with respect to input variables
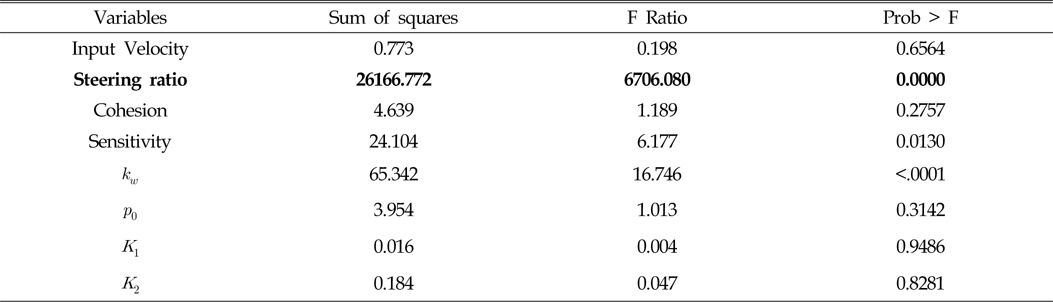
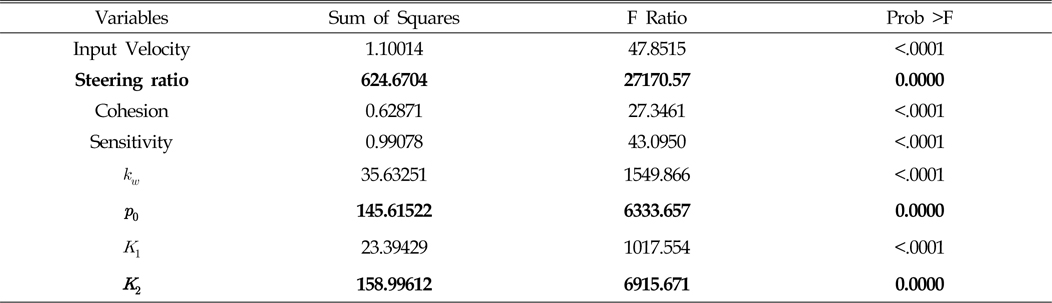
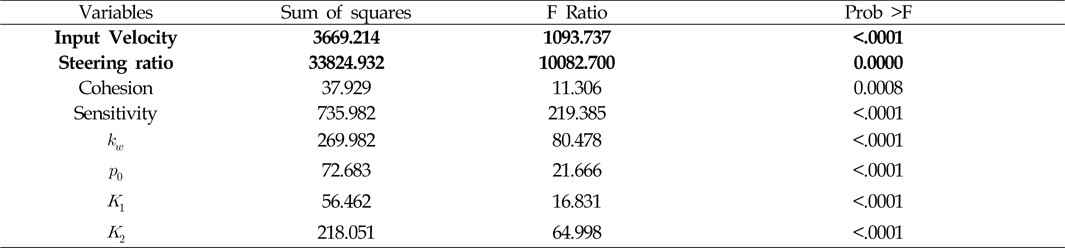
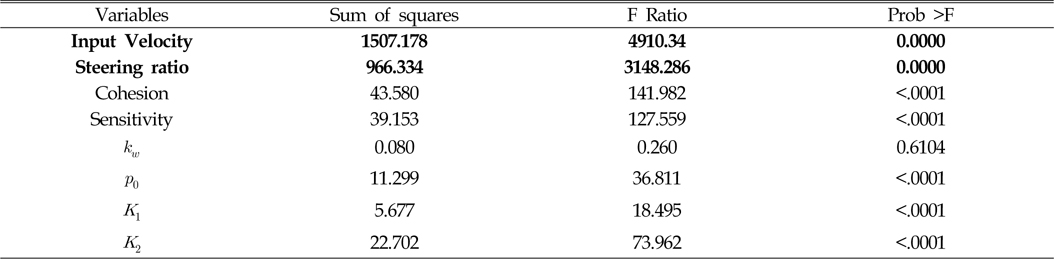
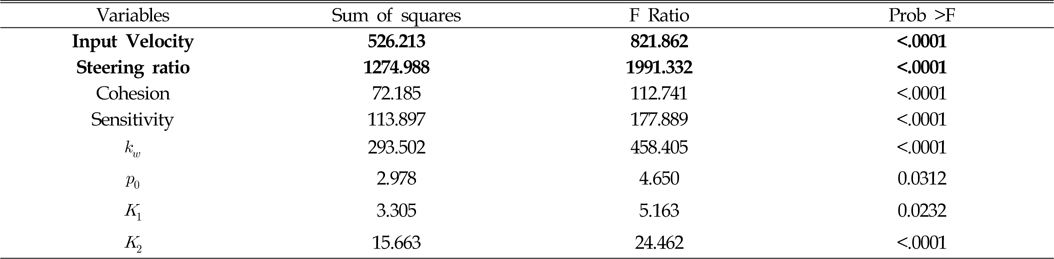
마지막으로 Table 7~10은 각 요소에 따른 슬립율의 영향도를 나타낸 결과이다. 이 결과에서 보듯이 슬립율에 영향을 가장 많이 주는 값은 선회비와 기준 속도임을 알 수 있다. 이때 각 궤도에 따라 영향도가 다르게 나타남을 확인 할 수 있는데, 가장 바깥쪽 두 궤도(Fig. 6에서 T3, T4 궤도)에서는 선회비가 가장 큰 영향을 주며, 안쪽 두 궤도(Fig. 6에서 T1, T2 궤도)의 슬립율에는 입력 속도가 가장 큰 영향을 미침을 확인 할 수 있다. 또한 각 궤도에 따라 영향을 주는 인자가 다름을 확인할 수 있다. 하지만 주로 전단응력-전단변위 관계식의 입력 계수가 압력-침하 관계식의 입력 계수보다 더 큰 영향을 미치고 있음을 알 수 있다.
[Table 7] Analysis of effect for slip ratio of track 3 with respect to input variables
Analysis of effect for slip ratio of track 3 with respect to input variables
[Table 8] Analysis of effect for slip ratio of track 1 with respect to input variables
Analysis of effect for slip ratio of track 1 with respect to input variables
[Table 9] Analysis of effect for slip ratio of track 2 with respect to input variables
Analysis of effect for slip ratio of track 2 with respect to input variables
[Table 10] Analysis of effect for slip ratio of track 4 with respect to input variables
Analysis of effect for slip ratio of track 4 with respect to input variables
4. 결 론
본 논문에서는 파일럿 채광로봇 미내로에 대한 선회 주행 특성을 분석하기 위하여 측정 및 CAD모델을 통하여 실제 모델과 유사한 차량 입력데이터를 얻고, 실제 실험을 통하여 측정하기 어려운 토양모델 계수를 변화시키면서, 다양한 해석 조건에 따른 선회 특성을 분석하였다. 또한 많은 해석조건에 따른 해석 시간을 줄이고자 직교배열표를 사용하였다. 그 결과를 다음과 같이 정리할 수 있다.
(1) 선회 반경의 경우 선회비의 영향을 가장 많이 받으며, 또한 이밖에도 주로 전단응력-전단변위에 해당하는 변수의 영향을 받는다.
(2) 침햐량의 경우도 역시 선회비의 영향을 가장 많이 받으며, 또한 선회반경과는 달리 주로 압력-침하에 해당하는 변수의 영향을 받는다.
(3) 슬립율의 경우 주로 선회 기준 속도 및 선회비의 영향을 크게 받으며, 이밖에 각 궤도의 위치에 따라 결과에 영향을 미치는 인자는 다르다.
향후에는 실해역 실험에서 얻어진 선회주행 결과와의 비교를 통하여 실해역에서의 토양 데이터를 예측하고, 본 논문에서 고려하지 않은 해류 및 경사면 등 다양한 환경조건에 대한 미내로의 주행특성을 분석할 예정이다.