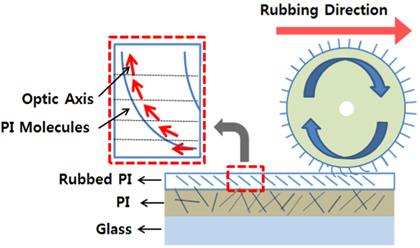
Rubbing is the process to make an alignment layer, which dictates the molecular arrangement of the liquid crystals (LC) of a liquid crystal display (LCD). In the process, cured polyimide (PI) films are rubbed with a velvet cloth and the surface state of this rubbed PI alignment layer governs the molecular arrangement of the LC, and hence directly affects color gamut and response time of the LCD. For these reasons, a lot of research has been carried out to understand the actual alignment mechanism of rubbing. To characterize the rubbed alignment layers, the precise surface sensitive techniques such as AFM (Atomic Force Microscopy), GIXS (Grazing Incidence X-ray Scattering) or NEXAFS (Near-Edge X-ray Absorption Fine Structure) are often engaged. One possible interpretation of the alignment mechanism of rubbing is the induced alignment by microgrooves [1-4] and another concept for the interpretation is alignment through the reordering of the long-chain organic molecules on the rubbed surface[5, 6]. Optical techniques are commonly applied to characterize the rubbing effect. However, most optical techniques are applied after LC injection since the optical anisotropy of the rubbed alignment layer is too small to be detected using conventional optical techniques [7-9]. In order to characterize the optical anisotropy of the rubbed PI surface itself, a polarization sensitive optical technique such as ellipsometry is used [3, 6, 10-17]. The frontier work of ellipsometric characterization was reported by Hirosawa. [10-12] In analyzing the ellipsometry data, Hirosawa adopted the model that the rubbed polyimide film is composed of a molecularly oriented upper layer and a random lower layer. He found that the thickness of the upper layer ranged from 12.0~13.5 nm and the tilt angle of the principle dielectric axis of the molecularly oriented upper layer was about 40 degrees. The tilt angle varies from 39 degrees to 53 degrees as the rubbing strength is varied, and it increased up to 67 degrees as the rubbed polyimide film is annealed [10-12]. Yang et al. used AFM to determine the mean depth (7.0 nm) of the rubbed PI layer. The mean depth was used to get an optical birefringence of that layer and they reported the birefringence as Δn = 0.17 [3]. The successive reports by Hirosawa et al. reveal that the thickness of the anisotropic upper layer is 36.1 nm for the actual panel, which is much greater than the previously reported one and it remains unchanged even when the rubbing strength is increased. When soaked in solvent, it decreases from 35.6~45.0 nm to 27.1~34.4 nm. The optical birefringence of a strongly rubbed polyimide and that of the weakly rubbed polyimide are reported as
Since it is not the bulk anisotropy but the surface anisotropy of the rubbed polyimide that governs the alignment of LC, finding the optical anisotropy distribution of the aligned molecules of the rubbed polyimide from the surface is very important. Hence the Hirosawa’s model, which uses a very simplified assumption that the surface of rubbed PI is a uniform anisotropic layer, needed to be modified. Meanwhile, a method to determine the optical anisotropy distribution has been reported already for a wide view (WV) film. It is reported that the optic axis of discotic liquid crystals in a WV film is distributed in the form of an exponential function, from the direction normal to the film surface to the direction parallel to it [18, 19]. However, since the magnitude of optical anisotropy of the rubbed polyimide is less than 1/100 of that of the WV film, one has to measure the ultra-small optical anisotropy extremely accurately in order to get the anisotropy distribution of the rubbed polyimide. In this work, we report that the same method which is used to determine the optic axis distribution of discotic liquid crystals in a WV film can be applied to determine the anisotropy distribution of the rubbed PI, when the measurement of very small optical anisotropy is made [17].
2.1. Polarization Analysis of a Non-Uniform Optically Anisotropic Film
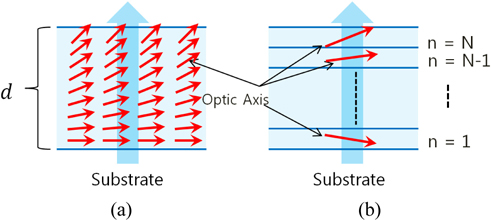
In relation with the rubbing direction of a rotating roller, organic molecules are expected to distribute as shown in Fig. 1 schematically. The optic axis of organic molecules is also expected to have the same distribution.
The change of polarization state of light after transmitting a non-uniform uniaxial film can be described by adopting the method which is used to determine the non-uniform optic axis distribution of discotic liquid crystals in a WV film [18-20]. We first replace the non-uniform uniaxial film in which the optic axis changes continuously, by a stack of
Here, and are Jones vectors representing the polarization state of the transmitting light and that of the incident light, respectively, and is a Jones matrix representing the change of polarization state by
In the above equation, the subscripts
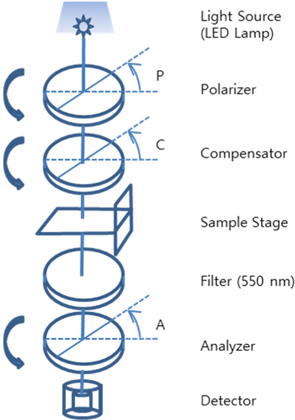
2.2. Rotating Analyzer Ellipsometer and Ellipsometric Constants
In PCSA configuration as shown in Fig. 3, the polarization state of light after passing through polarizing devices and sample can be written as shown in Eq. (3). In Eq. (3), the notation suggested by Azzam and Bashara is adopted [21, 22]:
Here, , is the rotation matrix, and is the Jones matrix representing the polarizing action of the non-uniform, anisotropic sample. The explicit expression of appears in Eq. (2). is the Jones matrix of compensator and A, C, and P represent the azimuth angle of analyzer, that of compensator, and that of polarizer, respectively.
The intensity of light can be obtained by taking the absolute square of . It becomes a sinusoidal function of the analyzer azimuth angle A. For the rotating analyzer type ellipsometer, A=ωt and the intensity of light is expressed as appearing in Eq. (4), where ω is the angular velocity of rotating analyzer [21, 22]. Since Fourier coefficient
For a uniaxially anisotropic sample, the variation of the polarization state of transmitted light versus the azimuth angle of the sample strongly depends on the incident angle. For example, if light is incident normal to the surface of an o-plate, then the ellipsometric coefficients
If the sample surface is inclined, then the light is incident on the sample surface at an oblique angle, and the angle of incidence is the same as the inclined angle of the sample. The periodicity of measured ellipsometric constants is dependent on the tilt angle
III. SAMPLE PREPARATION AND MEASUREMENT
The alignment layer is made on an ITO glass substrate by spin coating. The size of ITO glass is 25×25×0.5 mm3. The solution containing polyamic acid (Nissan 7492k) is coated on the substrates by using a spinning coater. Imidization is performed by curing at 250℃ for 60 min after prebaking at 80℃ for 15 min. Then the films on the ITO glass substrates are rubbed. The diameter of rubbing roller is 30 mm, the rotation speed of the roller is 1000 rpm, the stage speed is 25 mm/s, and the rubbing depth is 0.3 mm. The number of rubbing is two for all samples.
In order to find out the distribution of the ultra-small optical anisotropy whose total retardation is only 0.2~0.4 nm, the precision of the optical anisotropy measurement should be very high. This high precision measurement is achieved utilizing the improved transmission type ellipsometer whose precision to measure a retardation is 3σ < 0.005 nm. The major improvements made to this ellipsometer are, i) the structure of the ellipsometric system is changed from the conventional sample rotation type to the module rotation type, in which the polarizer module rotates while the sample is fixed, ii) the light source is replaced by one which emits a more stabilized light and therefore reduces the background noise level of the system, iii) the rotating polarizer module is synchronized with the rotating analyzer module very accurately, and iv) the tiny background optical anisotropy occurring in connection with the rotating modules is properly compensated [17]. In addition, we installed a dual-rotating sample stage onto this ellipsometer, thus one can set the incline angle of the sample from 0 to 60 degree up to the precision of 0.01 degree, and at the same time one can measure ellipsometric constants as a function of azimuth angle of the rotating sample. We also synchronized the zero point of the rotational sample stage with the rotating polarizer module and the independently rotating analyzer module simultaneously to get ellipsometric data as fast as 15 seconds per sample rotation.
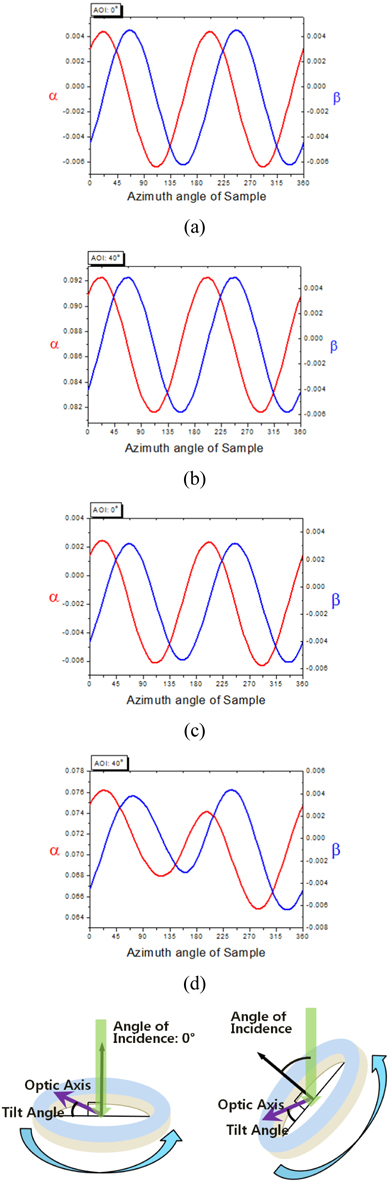
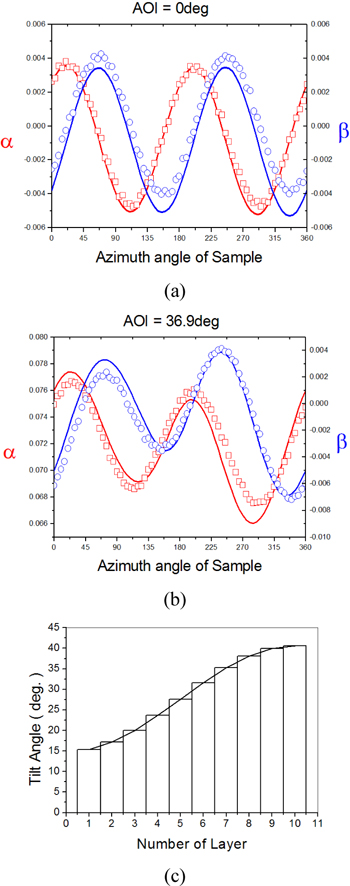
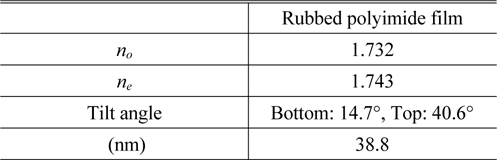
The measured ellipsometric constants of the rubbed PI sample are shown in Fig. 5, as open circles and open squares. The best fit ones obtained after model analysis are presented as solid lines. Figure 5(a) shows the graphs of
[TABLE 1.] The summarized optical anisotropy of the rubbed PI film
The summarized optical anisotropy of the rubbed PI film
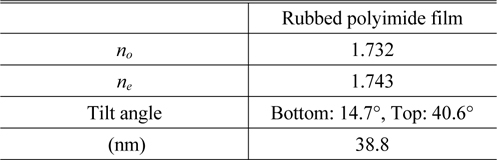
It might be possible that the tilt angle of the optic axis is expressed by a function other than Eq. (5). [18] But exponential ones or trapezoidal ones turned out to fit worse than the sinusoidal one in Eq. (5), only this best-fit tilt angle distribution is presented in Fig. 5(c). The optical birefringence (Δn =0.011) and the thickness of aligned layer (d=38.8 nm) is comparable to the previously reported values. [6-16] The incident angle (36.9 degrees) is a few degrees off from the incident angle set in the measurement system. This deviation is due to the fact that the measured ellipsometric constants are precise but they are not accurate enough and too many strong correlated parameters are used to get the best fit numbers in the model analysis. We expect that the accuracy of our model analysis will be enhanced when we further improve the accuracy of the ellipsometer and when we reduce the number of model parameters by fixing a few parameters(e.g., no and ne) at the numbers determined independently.
The transmission ellipsometric constants of a rubbed polyimide film versus the sample rotation angle are obtained at a normal incidence and at an oblique angle of incidence. The latter ones show a distorted sinusoidal variation. The magnitude of the optical anisotropy of this rubbed polyimide film and the distribution of the optical anisotropy are expressed in terms of the ordinary refractive index (