One of hot issues of solar-terrestrial physics is the prediction of intensity of geomagnetic storms and moments when they are occurring, which is a main problem of a subject now known as space weather forecast. Geomagnetic storms are phenomena that last a few days during which the geomagnetic field experiences rapid variations seriously affecting human activities (e.g., Eroshenko et al. 2010). The magnetic variations are a proxy for disturbances in the plasma populations and electric current systems present in the terrestrial magnetosphere. They are, however, responsible for at most around 1% of the total magnetic field that can be measured at the Earth’s surface. For instance, even in the severe cases they are between 400 and 700 nT against 40000 nT in normal regions. The primary energy source of the geomagnetic storm is the Sun which transfers energy to the Earth’s magnetosphere by means of solar wind. Energy from solar wind is injected into the Earth’s magnetosphere mostly in a case when interplanetary magnetic field (IMF) has a significant southward component (Cane et al. 2000). This magnetic field orientation allows magnetic reconnection and energy transfer from solar wind to the Earth’s magnetosphere. When accumulated energy reaches a certain level, any small disturbance outside or inside Earth’s magnetosphere can result in violent release of this energy as global reorganization of electric current systems of Earth’s magnetosphere and heating/acceleration of plasma. Although the geomagnetic storm has been attributed to solar phenomena for decades, the exact solar sources and their characteristics have not been well defined (e.g., Gonzalez & Tsurutani 1987, Wang et al. 2002, Cane & Richardson 2003, Correia & de Souza 2005, Yermolaev et al. 2007).
Temporal variations of such key parameters have been extensively investigated. Firstly, the 11-year solar cycle and associated variabilities have been studied in the last decades to understand actual mechanisms and processes for the observed geomagnetic storms. Periodicities of ~ 11 years, ~ 5.3 years, ~ 3.5 years, ~ 1.9 years and even shorter ones are found being meaningful using harmonic analysis of IMF parameters and/or geomagnetic activity indices (Kane 1997, Ahluwalia 2000, Clúa de Gonzalez et al. 2001, Kane 2005, de Artigas et al. 2006, Oh & Chang 2012, Cho et al. 2014). The solar cycle dependence of geomagnetic storm occurrence has been further studied. Geomagnetic storms are more likely to arise near the sunspot maximum and in the descending phase of the solar cycle as well (Gonzalez et al. 2007, Echer et al. 2008). Secondly, the annual geomagnetic activity distribution is frequently being reported, which is characterized with maxima around the equinoxes and minima near the solstices. The cause of this seasonal variation may be attributed to one or more of the three models known respectively as the equinoctial hypothesis, the axial hypothesis and Russell-McPherron mechanisms (Russell & McPherron 1973, Clúa de Gonzalez et al. 1993, Clúa de Gonzalez et al. 2002). Thirdly, a correlation between distributions and the corresponding geomagnetic storm intensities has been also found, which is actually regarded as a basis of solar-terrestrial connection. This finding could serve as a probabilistic storm forecasting method (e.g., Crooker & Gringauz 1993).
Yet another useful technique for solving problems in the subject of space weather is the calculation of frequency distributions of events, that is, occurrence rate, based on observations, whose form can be
2. DATA AND METHOD OF ANALYSIS
For the present analysis, firstly, we have used the mean daily speed of solar wind and the number density of protons (np in # cm-3) in solar wind during the period from February in 1999 to January in 2013. They are measured by the Solar Wind Electron, Proton, and Alpha Monitor (SWEPAM) on the Advanced Composition Explorer (ACE) spacecraft. Both data sets can be obtained from the ACE Science Center website
The present analysis is carried out using the superimposed epoch method for 10 parameters in total as listed in the next section (Kim & Chang 2014). To apply the technique for a selected parameter, we first chop the entire data-string of time series into several substrings with an appropriate length. Then we superimpose substrings and in turn average values of the parameter of interest for a given epoch, respectively. We end up with one single shortened data-string after this step of process. For instance, in comparing statistical properties at the solar maximum and minimum periods, we have 365 day long substrings. Or, in examining the dependence of the distribution on the annual variation we have 6 month long substrings because of 2 equinoxes and 2 solstices, respectively. Having done that, in order to construct the distribution function we need to count the number of values of the parameter of interest in each bin, resulting in a histogram. Note that the histogram is normalized such that the total area is equal to the unity. Finally, we fit the Gaussian function to the histogram by independently adjusting 3 parameters (amplitude, mean value, width) assuming a normal distribution of errors. We repeat the whole procedure for sub-samples into which the parent data sample is divided by the predetermined criteria. Details of each step in the procedure are slightly subject to the parameter we study. For instance, we have arbitrarily chosen the bin size depending on the parameter under examination. However, the conclusion we draw is insensitive to the details.
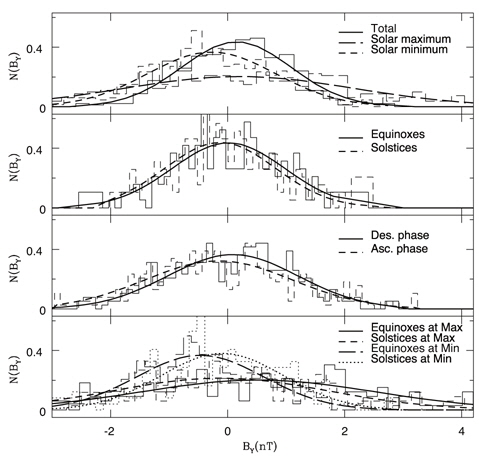
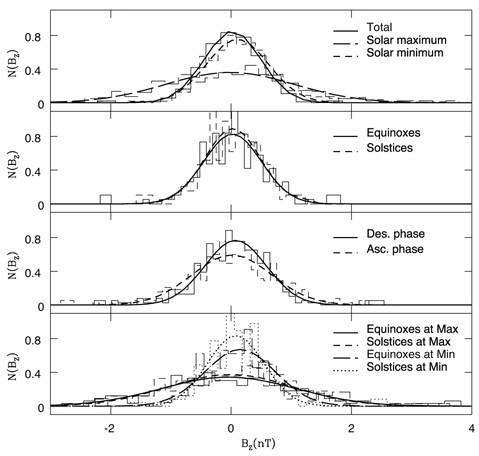
The analysis introduced in the previous section is carried out for the bulk speed of solar wind, he proton density in solar wind, magnitudes of the total IMF |B| and of its three components in the GSM coordinate system,
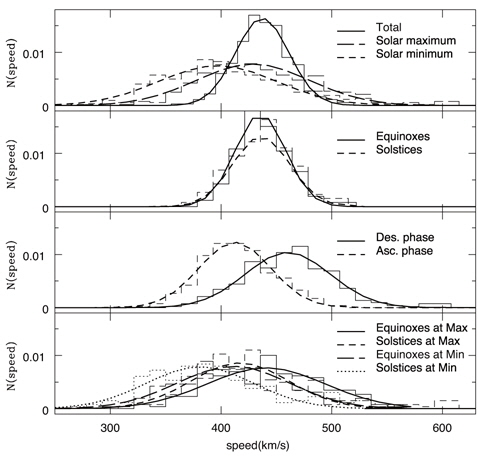
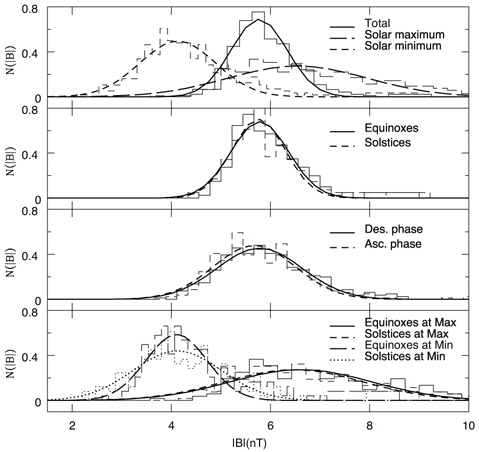
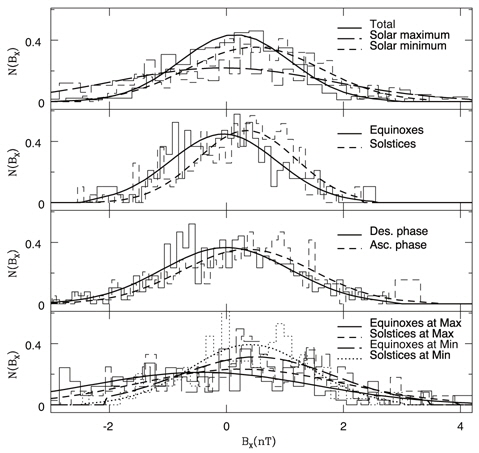
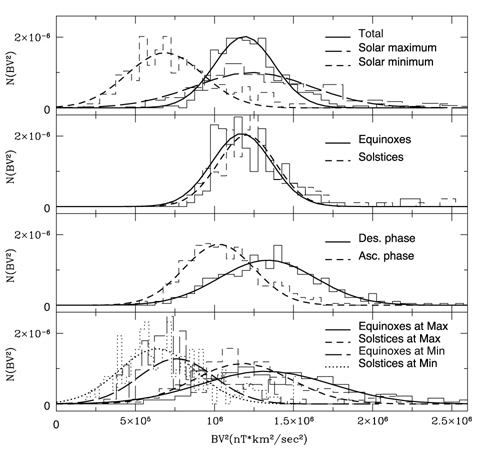
In Fig. 1, we show histograms of the speed of solar wind and their best fits obtained using the Gaussian function. In the top panel, we show histograms resulting from the whole data set of 14 year long duration and two sub-samples corresponding to the durations including the solar maximum (1999.02-2002.01) and the solar minimum (2008.02-2011.01), respectively. Solid, longdashed and short-dashed curves indicate the total data set, the subsets denoting the solar maximum, and the solar minimum, respectively. Thick curves represent the best fits of the Gaussian function to each histogram. Same line types represent same data sets. The Gaussian function is apparently a good approximation of the histograms. It is not a surprising result in the sense that according to the central limit theorem of the probability theory the Gaussian distribution originates as a result of summation of independent random quantities. According to the Gaussian fit, the mean value resulting from the subset of the solar maximum is greater than that of the solar minimum. This is not unexpected, either, since more frequent solar activities are expected in the solar maximum period (Gonzalez et al. 2007, Echer et al. 2008). It should be noted, however, that the full-width-at-half-maximum (FWHM) resulting from the subset of the solar maximum is larger than that of the solar minimum. Hence, we conclude that intense solar wind may be expected due to not only the large mean value but also the nature of the broad distribution. This fact also indicates that during the solar maximum period one may expect much slower solar wind with respect to its mean value somewhat equally with much faster solar wind. Fitting parameters are listed in Table 1.
[Table 1.] Gaussian parameters obtained with fittings to histograms.
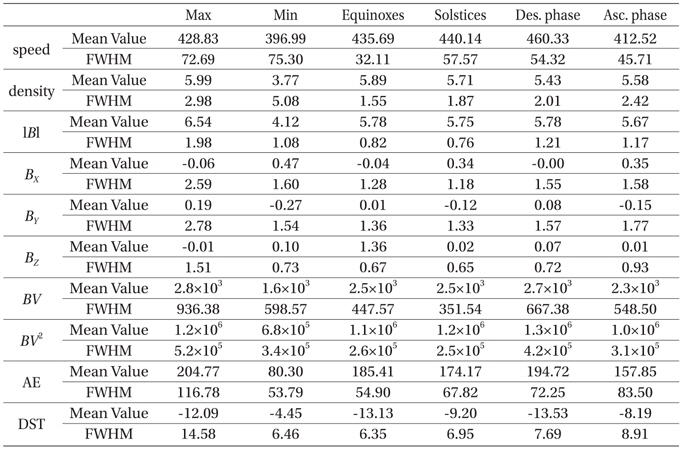
Gaussian parameters obtained with fittings to histograms.
In the second panel, we show histograms resulting from the two sub-samples corresponding to the durations including the two equinoxes (6 months of the year around the vernal and autumnal equinoxes) and the two solstices (6 months of the year around the summer and winter solstices), respectively. Solid and short-dashed curves indicate the subsets denoting the equinoxes and the solstices, respectively. Thick curves represent the best fits of the Gaussian function to each histogram. Same line types represent same data sets. Unlike other criteria in subgrouping the data sets a result here is somewhat different from what one might have expected. In other words, one is likely to expect the larger mean value and the FWHM for the sub-sample of the equinoxes than the solstices, since the annual geomagnetic activity distribution with maxima around the equinoxes has been reported in earlier reports (e.g., Clúa de Gonzalez et al. 2002). As a result of our analysis, as shown in the last panel, this effect is emanated more clearly when the data sets are further divided in terms of the solar maximum/minimum. Fitting parameters are listed in Table 1.
In the third panel, we show histograms resulting from the two sub-samples corresponding to the durations including the ascending phase of the solar cycle (1999.02-2002.01, 2009.02-2013.01) and the descending phase of the solar cycle (2002.02-2009.01), respectively. Solid and shortdashed curves indicate the subsets denoting the descending phase and the ascending phase, respectively. Thick curves represent the best fits of the Gaussian function to each histogram. Same line types represent same data sets. In this case, as seen in the solar maximum and minimum case, we find that the mean value and the FWHM for the sub-sample corresponding to the descending phase of the solar cycle are greater than the ascending phase. This finding appears to agree with earlier studies reporting that a physical condition of IMF is more chaotic in the descending phase than in the ascending phase of the solar cycle (Gonzalez et al. 2007, Echer et al. 2008). Fitting parameters are listed in Table 1.
In the last panel, we show histograms resulting from the four sub-samples corresponding to the durations including the two equinoxes (6 months of the year around the equinoxes) in the solar maximum (1999.02-2002.01) and in the solar minimum (2008.02-2011.01), and the two solstices (6 months of the year around the summer and winter solstices) in the solar maximum (1999.02-2002.01) and in the solar minimum (2008.02-2011.01), respectively. Solid, shortdashed, long-dashed and dotted curves indicate the subsets denoting the equinoxes in the solar maximum, the solstices in the solar maximum, the equinoxes in the solar minimum and the solstices in the solar minimum, respectively. Thick curves represent the best fits of the Gaussian function to each histogram. Same line types represent same data sets. Basically, what we see is what we may expect from plots shown in the first and the second panels. It apparently shows more clearly than the second panel characteristic features expected from the fact that the annual geomagnetic activity distribution has a maximum around the equinoxes. Fitting parameters are listed in Table 1.
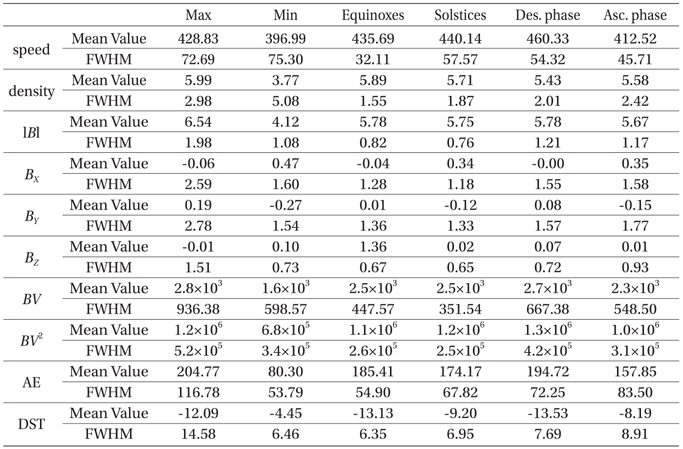
In Fig. 2, we show similar plots resulting from the proton density in solar wind. In this particular example, the distributions of the proton density seem comparable each other both in the descending/ascending phases of the solar cycle and in the equinoxes/solstices. On the other hand, they are distinct in the solar maximum/minimum according to the first panels. Fitting parameters are listed in Table 1. In Fig. 3, we show similar plots resulting from the total magnitude of the IMF |
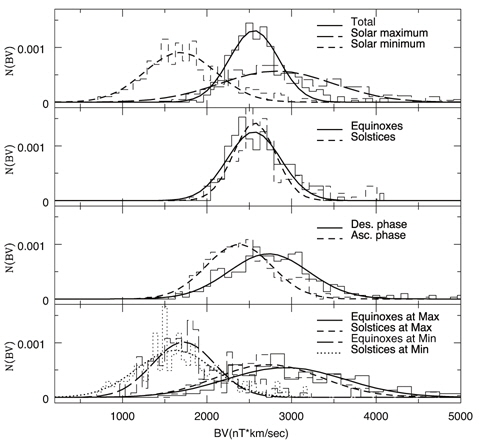
In Figs. 7 and 8, we show similar plots resulting from the approximate Kan-Lee merging electric field
Geomagnetic storms affect human activities in the modern age. Thus, the prediction of geomagnetic storms is becoming a more and more important and practical problem. An effective approach could be dealing with it as a probabilistic geomagnetic storm forecasting problem. To do so, one requires the occurrence probability function of a geomagnetic storm event for a given intensity. As a contribution to this line of efforts, we carry out detailed statistical analysis of solar wind parameters and geomagnetic indices in this study. Hoping to help in presenting a probabilistic model of geomagnetic storms, we have also examined the dependence of the distribution on the solar cycle and annual variations. The distribution of geomagnetic storms throughout the solar cycle and during the calendar year is a very important topic in space weather.
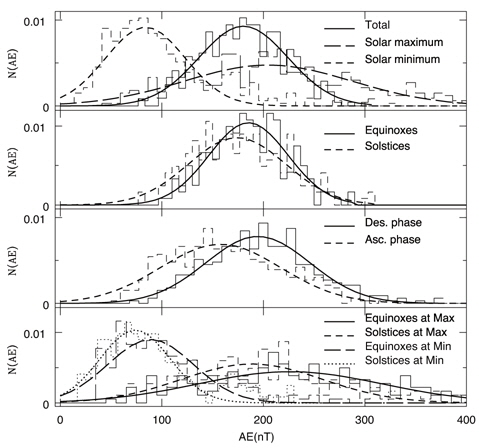
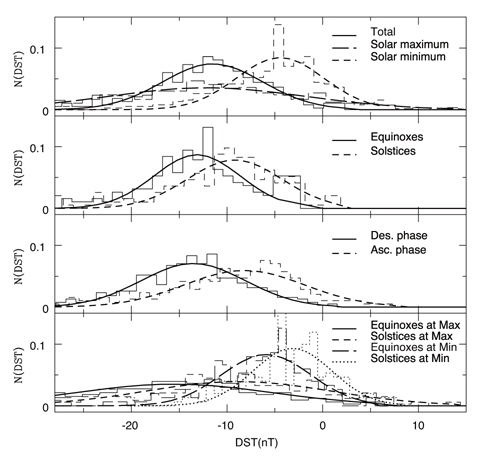
What we have found are as follows: (1) The distribution of parameters obtained via the superimposed epoch method follows the Gaussian distribution. It can be understood according to the central limit theorem of the probability theory. (2) The distribution of all the examined parameters is most sensitively dependent on the level of solar activity. When solar activity is at its maximum the mean value of the distribution is shifted to the direction indicating the intense environment. Furthermore, based on our analysis the width of the distribution becomes wider at its maximum than at its minimum so that more extreme case can be expected. (3) In general, the distribution of heliospheric parameters, such as, solar wind parameters and magnitudes of the IMF, is less sensitive to the phase of the solar cycle and annual variations. That is, the distributions seem comparable regardless of the descending/ascending phases of the solar cycle and in the equinoxes/solstices. (4) The distribution of the eastward component of the interplanetary electric field BV and the solar wind driving function BV2, however, appears to be all dependent on the solar maximum/minimum, the descending/ascending phases of the solar cycle and the equinoxes/solstices. Even in this case, the solar maximum/minimum is the most critical factor. (5) The distribution of the AE index and the Dst index shares statistical features closely with BV and BV2 compared with other heliospheric parameters. They are wider during periods of the solar maximum, the declining phase of the solar cycle and the equinoxes. In this sense, BV and BV2 are more robust proxies of the geomagnetic storm. As a result of our findings we conclude that our new results allow us to step forward in providing the occurrence probability of geomagnetic storms for space weather and physical modeling.