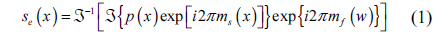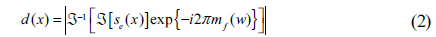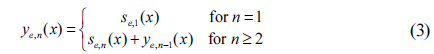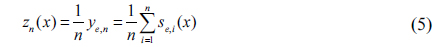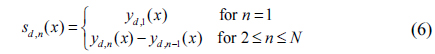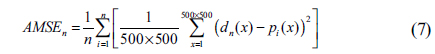Information security is one of the most important issues in data transmission. Optical encryption has been widely investigated for information security because of its high encryption speed [1-23]. As a representative optical encryption technique, double random phase encryption (DRPE) has been well studied [1-21] and improvements have been developed, such as DRPE using the Fresnel domain [2], DRPE using a full-phase processor [3], DRPE using digital holography [4, 5], photon-counting DRPE [6, 7], and DRPE using fractional Fourier transform [8-10].

Since DRPE uses double random phase masks for encryption, a security defect can be introduced [11], so updating the phase masks is required to resolve the security problem. However, such a resolution may lead to a cost problem. Therefore, advanced DRPE techniques without phasemask updating have been introduced [8-10, 18-21]. In particular, DRPE using fractional Fourier transform has been presented [8-10] to enhance the security of DRPE systems, where security is improved by increasing the number of encryption parameters. However, DRPE systems using fractional Fourier transform can be more complicated because of many encryption parameters. Hence, DRPE using orthogonal encoding has been presented as a low-complexity DRPE system in which the orthogonal encoder contains simple linear functions [20, 21].

In this paper we propose a DRPE-based accumulation encoding scheme for multiple-image transmission. It can be considered a low-complexity DRPE scheme because of the simple structure of its accumulation encoder and decoder. In addition, data security can be enhanced by introducing accumulation encoding into DRPE. We provide a detailed method for DRPE-based accumulation encoding and decoding, and show simulation results verifying that decryption of the image encrypted by the DRPE-based accumulation encoding scheme becomes more difficult as the number of accumulated images increases, even when the phase key used in DRPE is known.

The paper is organized as follows. Section II presents the concepts behind DRPE. The DRPE-based accumulation encoding scheme for multiple-image transmission is described in Section III. To verify this optical encryption scheme, simulation results produced by DRPE using accumulation encoding are provided in Section IV. Finally, we conclude the paper in Section V.

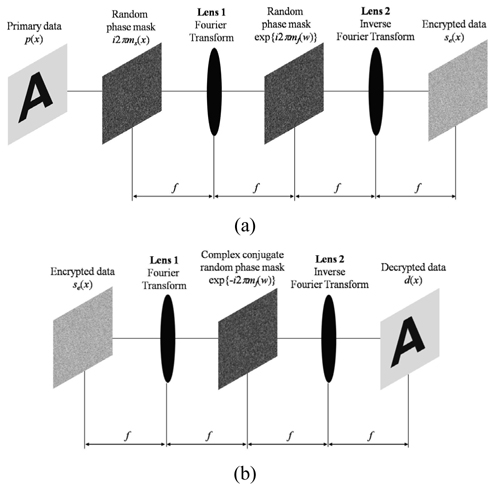
DRPE, an optical encryption technique, uses double random phase masks to encrypt data. Data encrypted by DRPE look like noise. For decryption, the key random phase mask used for encryption is required. For the sake of simplicity, in this paper we consider the encryption of one-dimensional data.

Let p(x) denote the primary data in the spatial domain, and let m_s(x) and m_f(w) represent the random phases in the spatial and spatial frequency domains respectively. m_s(x) and m_f(w) are uniformly distributed over [0, 1]. Figures 1(a) and (b) depict the schematic setup of encryption and decryption for DRPE respectively, where f is the focal length and two lenses are used for Fourier transform and inverse Fourier transform. As shown in Fig. 1(a), for encryption first the primary data is multiplied by the random phase mask exp[i2πm_s(x)] in the spatial domain. After passing the signal through the first lens we obtain ℑ {p(x)exp[i2π m_s(x)]}, where ℑ denotes the Fourier transform. Next it is multiplied by the random phase mask exp[i2πm_f(w)] in the spatial frequency domain. After passing through the second lens, the data encrypted by DRPE, s_e(x), are obtained as follows [6]:

where ℑ⁻¹ represent the inverse Fourier transform. Exploiting the characteristics of a complex-valued function, the encrypted data can be expressed as amplitude and phase parts, i.e. s_e(x) = |s_e(x)|exp[iφ_e(x)].

As shown in Fig. 1(b), for decryption the encrypted data are multiplied by the complex conjugate of the key information, i.e. exp[-i2πm_f(w)]. The decrypted data are then obtained as follows [6]:

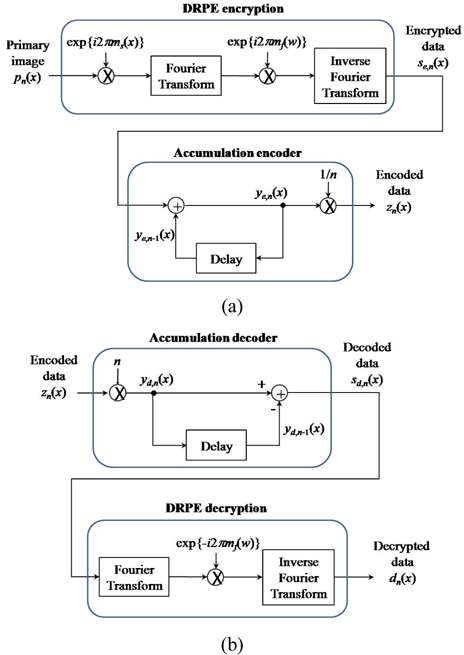
Figures 2(a) and (b) depict the schemes for DRPE-based accumulation encoding and decoding for encryption and decryption, respectively. As shown in Fig. 2(a), the n^th primary image p_n(x) is encrypted and encoded for transmission. It is noted that DRPE with the same random phase mask is used for encryption of all the primary images. The data encrypted by DRPE, s_e,n(x), are encoded with the accumulation encoding scheme as follows:

where y_e,n(x) represents the n^th encoded data. As seen in Eq. (3), for accumulation encoding all the previous encrypted data are added, which can enhance the security of the DRPE-encrypted data. Eq. (3) can be simply rewritten as

After accumulation encoding of the n^th encrypted data, the n^th encoded data are normalized by the factor 1/n, and finally the n^th encoded data z_n(x) are obtained as follows:

For perfect decryption of the accumulation-encoded data, as shown in Fig. 2(b), the encoded data are multiplied by n to scale it. Then the accumulation decoding is performed as follows:

where s_d,n(x) denotes the n^th decoded data and y_d,n(x) = nz_n(x). By inserting Eq. (5) into Eq. (6), we obtain s_d,n(x) = s_e,n(x), which means that the encoded data are perfectly decoded. The n^th decoded data are then decrypted by DRPE using the same random phase mask as for encryption. Finally the n^th decrypted data d_n(x) are obtained as d_n(x) = p_n(x).

The accumulation encoder and decoder require only a simple linear operation and storage to store the data with the size of a single image, as seen in Eqs. (3) and (6). Therefore, the addition of the accumulation encoder and decoder to the DRPE system requires low cost and effort.

To evaluate the performance of DRPE-based accumulation encoding we consider 20 primary images with 500(H)×500(V) pixels, as shown in Fig. 3. Figures 4(a)-(t) show the simulated results of DRPE-based accumulation encoding, meaning z_n(x) in Fig. 2(a). From the figures we can see that the accumulation-encoded images are perfectly encrypted because they look like noise. Figures 5 and 6 show the decrypted images without and with accumulation decoding respectively, where it is assumed that the DRPE key information is perfectly known for decryption. When no decoding is used, the encoded data are not decoded with the accumulation decoder but are directly decrypted by DRPE decryption; thus, s_d,n(x) = z_n(x). From Figs. 5(a)-(t), it is observed that when no decoding is used the image recognition becomes worse as the index of accumulation encoding n increases, even though perfect DRPE key informationis known for decryption. This also, means that accumulation encoding is able to improve the security of DRPE-encrypted data even when the DRPE key information is known. Figures 6(a)-(t) indicate that the encoded images are perfectly decrypted when correct decoding and decryption are performed.

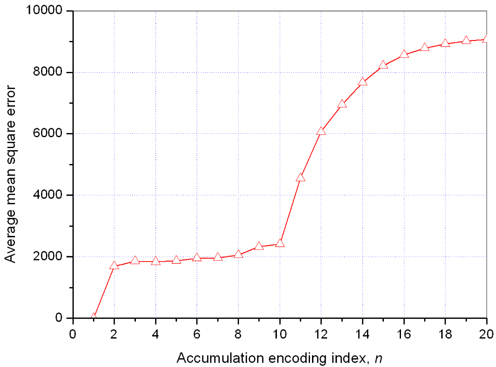
To quantify the differences between the primary images in Figs. 3(a)-(t) and the decrypted images without decoding in Figs. 5(a)-(t) respectively, mean square error (MSE) results are calculated, as shown in Fig. 7, where we assume that the image pixel values are integers ranging from 0 to 255. In Fig. 7 the average MSE for the n^th accumulation encoding is obtained as follows:

When no decoding is used, the n^th decrypted data d_n(x) contain the data for the 1^st through n^th primary images, as described in Eq. (5). Thus we show the average of MSE results between the n^th decrypted image and the 1^st through n^th primary images, as in Eq. (7). Figure 7 demonstrates that the average MSE increases with the accumulation encoding index n. Especially when n ≥ 11 the average MSE increases greatly because the 11^th through 20^th primary images have a different color pattern than the 1^st through 10^th primary images. From these results it can be seen that the encoded data become more secure as the accumulation encoding index rises, even though the DRPE key is known in decryption. However, for the first accumulation encoding the MSE result is zero, as the decrypted data contain only the data for the first primary image.

We propose a DRPE-based accumulation encoding technique for multiple-image transmission. In particular, we present the schemes for encryption and decryption for DRPE-based accumulation encoding and decoding, respectively, and methods for accumulation encoding and decoding. The simulation results verify that DRPE-based accumulation encoding for multiple-image transmission can enhance the security of DRPE-encrypted data when the key information of DRPE is perfectly known in decryption. Furthermore, since the accumulation encoder and decoder require only a simple linear operation and enough storage to hold a dataset of a single image, the DRPE system with accumulation encoding can be implemented with little cost and effort.