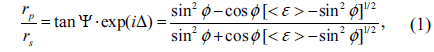Langmuir monolayers provide a unique means to study two-dimensional (2D) materials at asymmetric interfaces. Investigations of Langmuir monolayers have uncovered a rich variety of physical phenomena [1-4]. When a 2D film is compressed to its stability limit, it explores the third dimension by collapse. 2D monolayers of a large number of amphiphiles transform into overgrown 3D structures in a state of metastability and supersaturation [5]. The mode of collapse can be tuned by varying the mechanical properties of the film. Understanding this 2D-to-3D transition is of great importance, as it provides insight into the origin and nature of defects in thin films such as the biological films that protect our eyes [6, 7], ears [8, 9], and the inner surface of our lungs [10-12].

The more common system of fatty-acid Langmuir monolayers forms very rigid films at high pressures, and one can imagine their behavior upon collapse would be different from that of monolayers of lung surfactant [13]. The microscopy and rheology of the collapse phenomenon in a single-component system of fatty acids is a simpler problem, one that has allowed the folding and collapse phenomena to be modeled [14, 15]. The changes in structure of collapsed films of fatty acid molecules having different chain lengths under different compression rates, temperatures, and subphase conditions (pH and salt species) have also been investigated [3, 16-20]. The π-A isotherms and the structure of the collapsed films are strongly affected by these various experimental parameters.

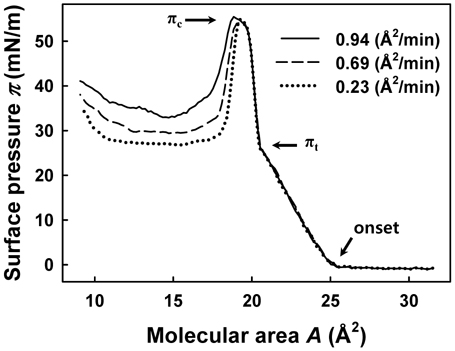
In this work we focus on the effect of compression rate. We use imaging ellipsometry (IE) [21-23] to characterize monolayer collapse physically as a function of the rate of molecular area compression from 0.23 to 0.94 Ų/min per molecule. IE is a noninvasive, in situ technique, unlike electron microscopy or atomic force microscopy. However, in contrast to conventional ellipsometry, which measures the average property of the surface over the size of the probe beam, IE obtains local ellipsometric values of the size of an image with a spatial resolution of a few μm, depending on the optics used. These values can be converted to film thicknesses at the same resolution. Whereas fluorescence microscopy [24] or Brewster-angle microscopy can also provide 2D images of collapsed films, the ellipsometric method that we use in this study adds value by yielding information about the third dimension of the individual domains, specifically their thicknesses.

For numerous insoluble monolayers, π-A isotherms of amphiphiles are in a metastable state above the equilibrium surface pressure. Thus in our studies we used IE to determine the changes in structure of the collapsed films as a function of the rate of molecular area compression. As expected, the surface after collapse was found to be very inhomogeneous, with coexisting regions of monolayer and multilayer films.

Arachidic acid (CH₃(CH₂)₁₈COOH, ≥99%, AA for short) is a saturated fatty acid with a carbon chain of 20 atoms. Our material was purchased from Sigma-Aldrich. AA was suspended and stored in a chloroform/methanol (HLPC grade, Sigma-Aldrich) 3:1 mixture in a freezer (−20℃) until use. It was spread onto organic-free deionized water of high resistivity (18.2 MΩ·cm, pH 5.7) in a custom-built Langmuir trough. Compression was begun about 15 minutes after spreading to ensure complete evaporation of the solvent. The Langmuir trough was put in the sample position of the IE and the surface was imaged in situ as the AA film progressed from a monolayer to multilayers. All IE measurements were carried out at room temperature (20℃). The rate of molecular area compression ranged from 0.23 to 0.94 Ų/min per molecule and was controlled by varying the speed of the barrier motor.

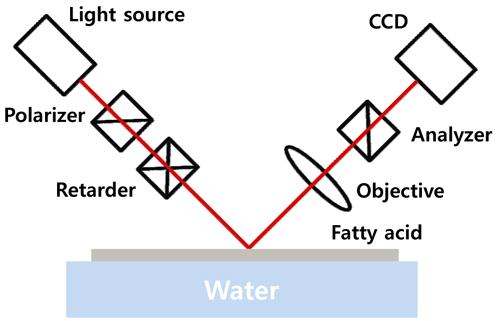
The IE used in this experiment was a rotating retarder type, manufactured by Beaglehole Instruments, Inc., New Zealand. The configuration is shown in Fig. 1. The wavelength was 632.8 nm and the angle of incidence (AOI) was 53.18°, which is the Brewster angle of water. The measured image covered a sample area of 1.8 × 2.7 mm with 200 × 500 pixels. An objective lens with a large numerical aperture (NA) would collect the light from the sample over a wider angular range, but also would increase the uncertainty of the incidence and reflection angles and thus decrease the resolution in the vertical direction (see the IE image of Fig. 5). To compromise between horizontal and vertical resolutions, the numerical aperture was kept at ~0.18. In this configuration each pixel corresponds to ~9 and ~5.4 μm for the vertical and the horizontal lengths respectively, for a wavelength of 632.8 nm. To avoid a large AOI error, we used a test beam a few mm in size in the vertical direction. The error bound of AOI is about ±0.6°. To minimize uncertainty, we averaged 11 chargecoupled device (CCD) images taken at analyzer angles of +45° and −45°. Typical exposure time was 100 ms for each CCD image. It takes 20 seconds to measure one frame of an IE image.

Figure 2 shows π-A isotherms of an AA Langmuir monolayer on water, measured using the Wilhelmy plate method with compression rates from 0.23 to 0.94 Ų/min per molecule. The isotherms are in good agreement with those in previous reports [5, 16-21, 25]. Before collapse, the onset point of an area of about 25 Ų per molecule and tilted-untilted transition pressure (π_t) area of 20.5 Ų per molecule are similar to those in previous reports. After collapse, the isotherms exhibit higher values of surface pressure with increasing compression rate. A transition from a surface pressure “spike” to a “plateau” was induced by faster compression at maximum surface pressure (π_c) [16-19]. IE measurements were performed in-situ after film collapse to obtain images on the monolayer scale of the film undergoing collapse.

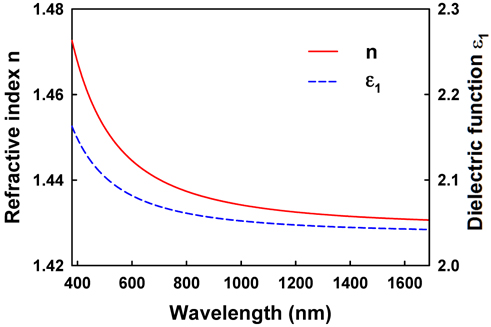
For the analysis of the collapsed monolayers, the dielectric function of AA is required. We obtained this using conventional spectroscopic ellipsometry (SE) [26]. SE measures Ψ and Δ, which are determined from the ratio of the complex reflectances of s- and p-polarized light and can be converted to the pseudodielectric function < ε> = < ε₁> + i< ε₂> given as [27]

where ϕ is the AOI and r_s and r_p indicate the complex reflectances for s- and p-polarized light respectively. Using the Langmuir trough we made an AA monolayer of area 19 Ų/molecule, then acquired in situ SE data using a model RC2 SE instrument (J. A. Woollam Co., USA). The original data bear information about both the complex refractive index (ñ= n + ik) and the film thickness. Here ε = ñ². To obtain ñ and thickness of the AA film, we fitted the data using a multilayer calculation [27] with a three-phase model consisting of air, the AA monolayer, and water. We adjusted the fitting parameters to minimize the mean square error (MSE) which is defined as

where the number of measured Ψ and Δ pairs is N, the total number of real-valued fit parameters is M, and and are the experimental errors of Ψ and Δ respectively. A Cauchy dispersion relation [28] was used to represent the dielectric function of the monolayer. With this procedure we obtained the dielectric function of AA from 380 to 1690 nm. The calculated AA monolayer thickness was 28.0 ± 1.5 Å, in good agreement with previous reports [20, 25, 29]. In previous work [25] data were obtained only at 632.8 nm, where a refractive index n = 1.4461 and extinction coefficient k = 0 were found. We emphasize that we observe not only a similar refractive index at 632.8 nm but also the entire dielectric function of AA over a much wider spectral range. Figure 3 shows the refractive index n and real part of the dielectric function ε₁ of AA that we obtained.

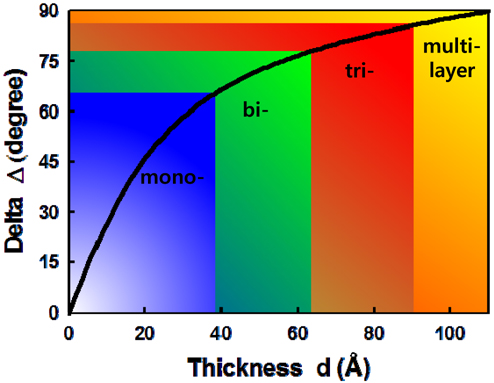
In IE we measured the same parameters introduced for conventional SE above, but a two-dimensional array of the pairs of ellipsometric parameters (Ψ, Δ) are obtained over the sample surface, which assess the properties of the sample at the scale of the resolution of the image. Thus IE is particularly suitable for probing the third dimension of the inhomogeneous layer [30, 31]. For layers appreciably thinner than the wavelength of the probing light, Δ is sensitive to change in layer thickness, while the Ψ value is hardly affected [25, 30]. With n = 1.44 for AA and n = 1.33 for water at 632.8 nm, the connection between Δ and thickness is shown in Fig. 4. To obtain the relationship, we calculated total reflectances of r_s and r_p with a threephase model (air/AA layer/water), varying the AA layer thickness using a multilayer calculation [27], and therefore the Δ values for different thicknesses can be extracted from Eq. (1). Thus all our IE images are those of Δ. To better visualize the thicknesses of the collapsed regions, mono-, bi-, tri-, and multilayer regions are color-coded separately with the boundary values of Δ set at the respective midpoints: Δ = 56, 72, 82, and >82° for mono- (28 Å), bi- (50 Å), tri- (75 Å), and multilayers (>75 Å), as shown in Fig. 4. The monolayer thickness was taken from our conventional SE result, while the thicknesses for bi- and trilayers are obtained from published x-ray and neutron reflectance measurements [20, 29]. The monolayer thickness corresponds to the length of the all-trans AA molecule, while the thicknesses for bi- and trilayers are slightly smaller than twice and three times of the AA monolayer length.

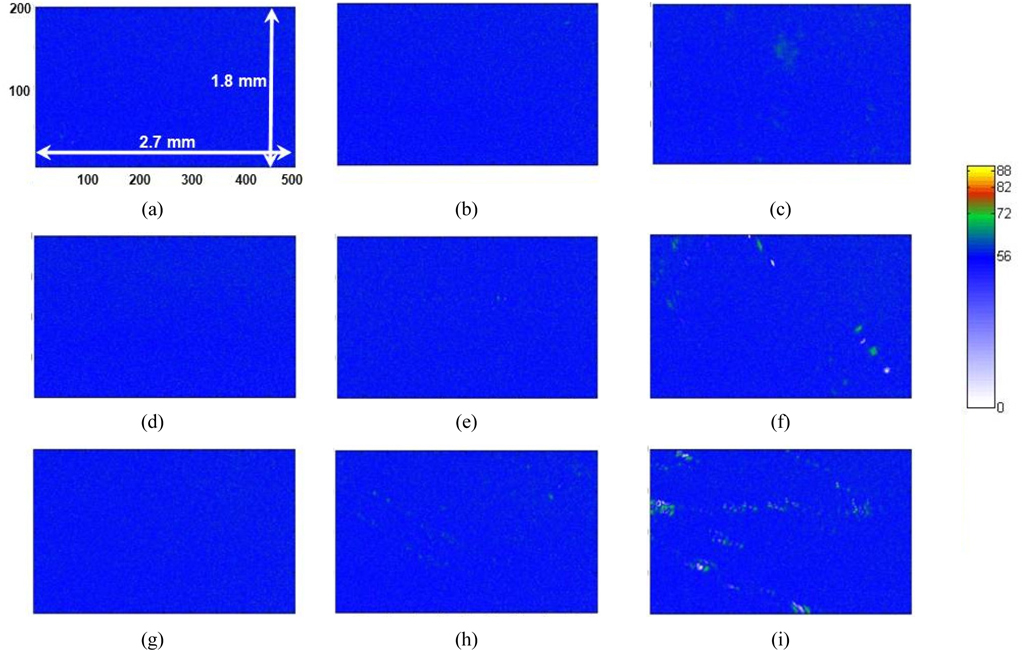
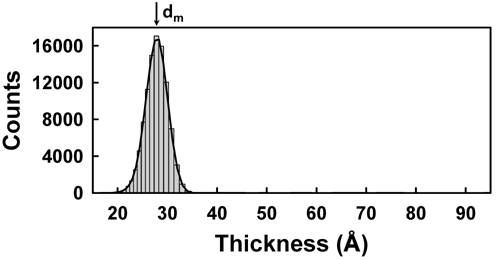
Figure 5 shows Δ images of 200×500 pixels of AA monolayers with several different values of molecular areas in condensed and after-collapse states for areas per molecule of 19.5, 18.6, and 17.5 Å2, respectively. The compression was performed in the vertical direction of the presented IE images. In Figs. 5(a), (d), and (g), the overall blue color of the images indicates that the surface is covered by a monolayer. As the molecular area decreases, a careful examination of Figs. 5(c), (f), and (i) shows that small dots with Δ values appreciably higher than those of the monolayer begin to appear, indicating that the layer thickness is not uniform over our detection area of 1.8 × 2.7 mm. This can be understood as the coexistence of the condensed phase (blue regions) and the collapsed phase (dark green regions). We statistically analyzed the data for the distribution of the AA layer thickness in corresponding areas. Figure 6 shows the pixel histograms of the corresponding image of Fig. 5(a), which consists of 0.1 million CCD pixels. We counted the pixels of equal Δ values with equidistant intervals of 1°, because the Δ is the original experimental data. In Fig. 6 the histogram indicates the distribution of film thicknesses within the probed area. We label the x-axis with thicknesses for clarity, using the relation obtained in Fig. 4. As shown in Fig. 6, the center value of the histogram corresponds to the thickness of the monolayer dm, and the peak widths correspond to the thickness variation over the probed area. The uniform distribution indicates the credibility of the IE data.

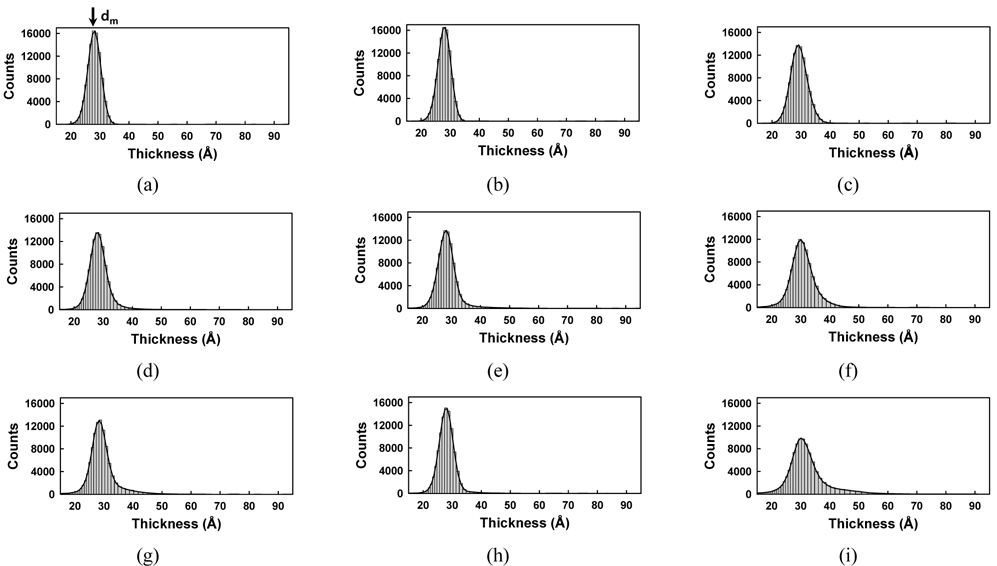
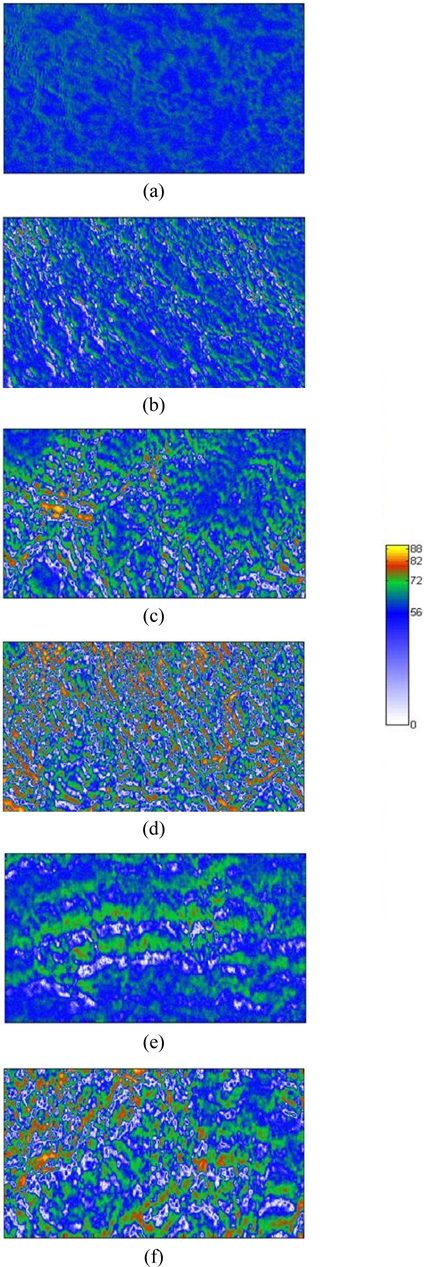
Figure 7 presents a collection of Δ images in the collapsed phase (a-c), (d-f), and (g-i), which correspond to per-molecule compression rates of 0.23, 0.69, and 0.94 Ų/min respectively. The area per molecule in Figs. 7(a), (d), and (g) is 15.6 Ų, that in Figs. 7(b), (e), and (h) is 13.4 Ų, and that in Figs. 7(c), (f), and (i) is 11.5 Ų. Figure 7 shows that some green regions with Δ values appreciably higher than that of the monolayer are present. The image of Fig. 7(a) (0.23 Ų/min per molecule compression rate) shows only a few small, collapsed dark green domains. Increasing the compression rate yields many more collapsed light green domains, appearing particularly in Figs. 7(d) (0.69 Ų/min) and (g) (0.94 Ų/min). Bilayer domains, appearing in green, increase as the film is further compressed. At the compression rate of 0.94 Ų/min some trilayer domains (red) become more numerous, as shown in Figs. 7(h) and (i). Very large Δ values are associated with multilayers. Consequently, the green and red dots in Fig. 7 are assigned to the spontaneous formation of multilayers [5, 19, 32].

The molecular mechanism assumes that over compression leads to bilayer domains merging with monolayer parts, yielding trilayer domains [32, 33]. Consistent with the simulation of Ref. [32] for AA on water, additional AA molecules move onto the AA monolayers, while at the same time head groups of AA molecules combine with each other due to hydrogen bonding. Upon further compression, more AA molecules are present and strong van der Waals forces cluster the hydrogen-bonded AA molecules into trilayers. According to Ref. [33] the combination of AA head groups yields bilayers, which form “towers”, thereby making trilayers on monolayers. Our experimental results correspond more closely to the theoretical simulations in Ref. [32].

It is clear that compression rates strongly affect the formation of multilayers. As expected, molecules that are moved more slowly, i.e., at smaller compression rates, yield more stable multilayers. Moreover, the collapsed regions in Fig. 7 are similar in shape to the light-blue regions associated with water, indicating that molecules in nearby monolayer domains are a reservoir for forming multilayer domains, as shown in a previous report [21].

Figure 8 shows the corresponding histograms for the images of Fig. 7. In Figs. 8(d) and (g) the thicknesses have a wider distribution than in Fig. 8(a), which means that the monolayers have collapsed and been transformed to multilayers. The histograms exhibit increasing widths and larger thicknesses with decreasing surface area.

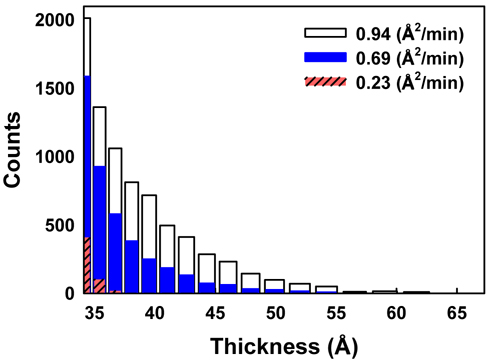
It is interesting to note that the tails of Figs. 8(a), (d), and (g) differ significantly, as shown in Fig. 9, where only the right-hand-side tail parts are compared carefully. In the case of a small compression rate of 0.23 Ų/min (red striped bar) the tail ends quickly, meaning that relatively uniform layers are formed. However, when the compression rate is high (white bar), the tail reaches the maximum thickness value, nearly 60 Å, showing the existence of thick multiple layers. This clearly suggests that AA monolayers spontaneously form multilayer domains more easily at higher compression rate.

Figure 10 shows the fully collapsed morphology of films with surface areas reduced to 10.4 and 9.5 Ų/molecule. This molecular area is approximately half of the area of the intact monolayer and could not be reduced further, due to the limitations of the trough and the beam geometry of our IE configuration. The image shows that the film is indeed very inhomogeneous, being covered by spatially separated multilayer domains. The average collapsed layer thickness is more uniform for films compressed at a slower rate. Clearly the different compression rates affect both the underlying domain structure and the collapsed phase.

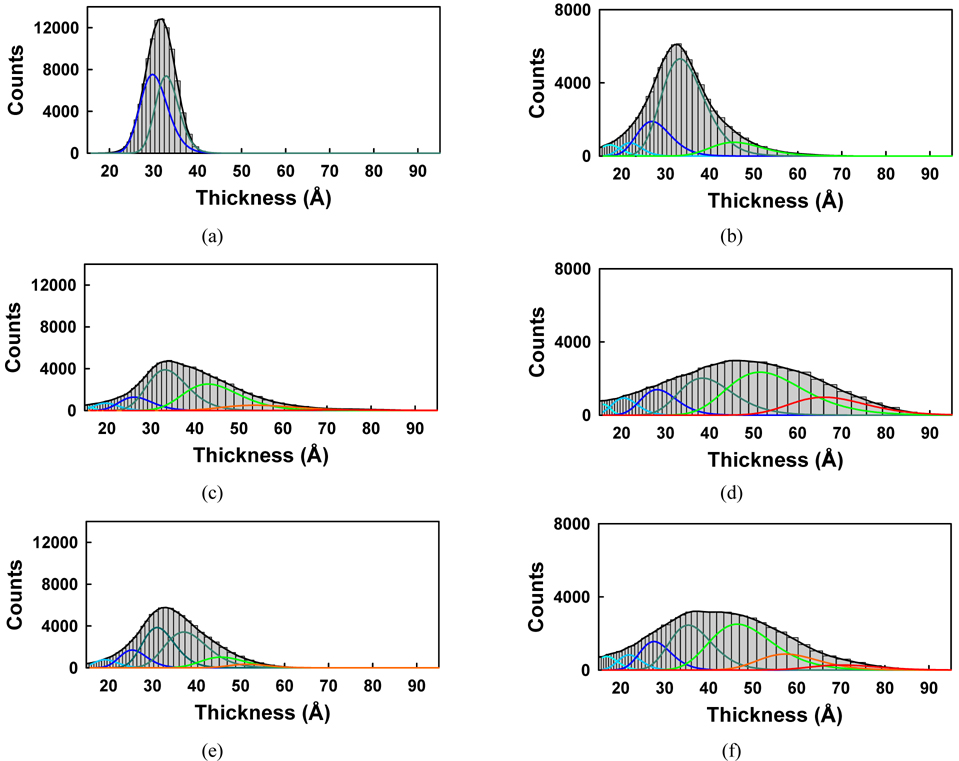
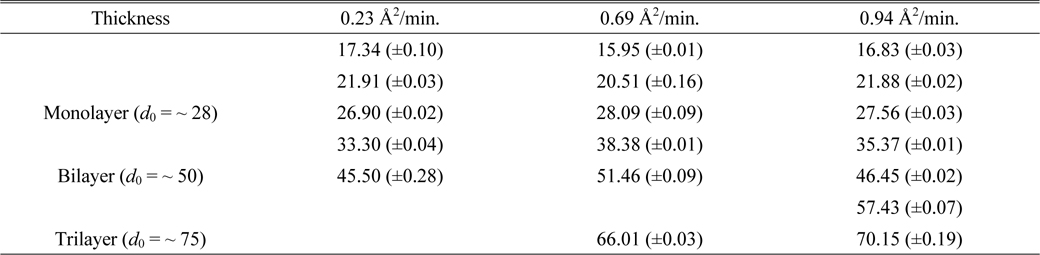
Figure 11 shows the corresponding histograms for the images of Fig. 10. To analyze the thicknesses of these samples more quantitatively, the histograms were fitted with multipeak Gaussian functions. Initially we tried to use only three peaks with d₀ values fixed at those corresponding to the thicknesses of mono-, bi-, and trilayers, but it immediately became clear that additional peaks at lower and higher d₀ values were needed to achieve a reasonable fit, indicating that multilayer formation necessarily involves peaks of thicknesses different from those of collapsed monolayers and bilayers. We then allowed the d₀ values to vary; the results are shown as the solid lines in Fig. 11. The agreement is excellent. The AA layer thicknesses found by fitting are not integer multiples of the monolayer thickness, indicating that the molecules in the multilayers are not oriented parallel to the surface normal [20, 25, 29,34]. 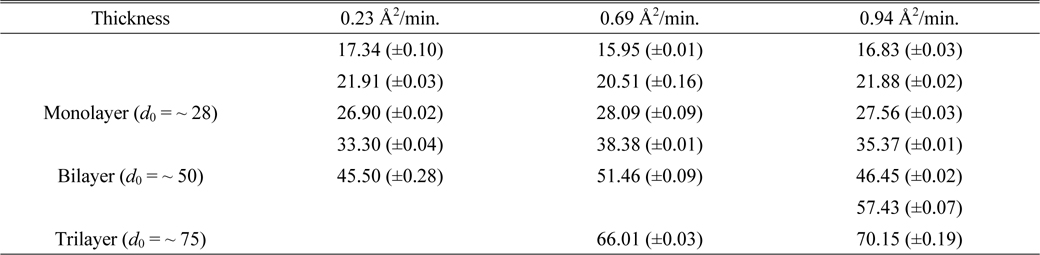The fitting parameters yielding the Gaussian peak positions in Figs. 11(b), (d), and (f) are listed in Table 1. We note that small magnitudes of uncertainty in all the parameter values suggest the uniqueness of the fitting, supporting the current analysis. For the image in Fig. 10(b) the thicknesses for the lower compression rate are relatively uniform, while for the higher compression rates of Figs. 10(d) and (f), the thicknesses are more random. It is clear that collapse is a kinetic process, and the compression history changes the structure of the films substantially.

Using IE, we observed detailed images of the thicknesses of AA molecular films on water after collapse with per-molecule compression rates of 0.23, 0.69, and 0.94 Ų/min. To analyze the thicknesses of the AA Langmuir layers we obtained the refractive index of an AA monolayer by conventional SE. The images show that some regions of the monolayer undergo spontaneous collapse more readily at higher compression rates. As the film is further compressed, multilayer domains form and grow as the surface area available to the film decreases. The analysis of the image at the smallest nominal molecular area of 9.5 Ų/molecule indicates that the thickness of collapsed film is more uniform at slower compression rates. In other words, under faster compression rate the film has no time for relaxation to form multiple layers of high thickness. Therefore, this observation suggests the existence of some relaxation mechanism of the AA film, indicating that a further study of the effect of compression rate using IE is needed, to analyze the relaxation time of the film. We find that its imaging capability makes SE an excellent method for studying inhomogeneities in such a system. We expect that in the future SE will find many applications in examining a wide range of subjects such as nucleation, domain structure, and film collapse.