Fermi Large Area Telescope (LAT) observations have revolutionized the study of rotation-powered pulsars, which are the dominant GeV γ-ray source class in the Galaxy (Abdo et al. 2010a). Since launch in 2008, new γ-ray pulsars have been discovered at an astonishing rate, and the discovery of new pulsars through blind frequency searches of γ-ray data alone has been a huge success (Abdo et al. 2009b). Another new γ-ray source population discovered by Fermi in its first six months of operation are the millisecond pulsars (MSPs) (Abdo et al. 2009c). All of these have been discovered through their radio pulsations, as the fact that 80% of MSPs are in binary systems makes blind period searches in γ-rays very difficult if not impossible. However, many new radio MSPs have been recently discovered in Fermi unidentified sources (Ransom et al. 2010). These new Fermi -assisted searches have so far netted 46 new MSPs, nearly doubling the number of MSPs in the Galactic plane. The majority of these are very nearby (< 1 kpc), at high Galactic latitude, and in binary systems, including 8 new “black-widow” MSPs that are interacting with and ablating their companions. The combined population of γ-ray pulsars presently numbers over 130, a factor of nearly 20 larger than before Fermi (Ray 2013).

With the large increase in new data, the time is ripe for uncovering the secrets of pulsars: the global current circulation in their magnetosphere, where they accelerate particles, how they radiate, the shape of their magnetospheres and their energetics. For more than forty years, the development of a variety of pulsar emission models has progressed slowly, in the absence of enough data to rule any out or distinguish among them. The emission developed along two major paths. Polar cap models (Ruderman & Sutherland 1975, Daugherty & Harding 1982) assume that acceleration takes place near the neutron star surface at the magnetic polar caps, where large electric fields are induced. Acceleration also takes place in a slot gap along the last open field line up to high altitudes. The high-energy radiation occurs within a few stellar radii of the surface since the particles lose their energy rapidly, and also in the slot gap from the neutron star surface up to the light cylinder. Outer gap models (Romani & Yadigaroglu1995, Cheng et al 2000) assume that particle acceleration and high-energy emission take place in vacuum gaps that develop along the last open field lines above the null charge surface to very high altitude. In this review, I will discuss the the polar cap and slot gap model for high-energy radiation, and its predictions in light of the new Fermi data.

Polar cap accelerators are based on the concept of “starvation” electric fields, where the space charge above the polar cap is not sufficient to maintain force-free (E·B=0) conditions. The force-free charge density, ρ_GJ=-Ω·B/2πc, for a dipole field and r？R_lc, where Ω is the pulsar rotation rate and R_lc=c/Ω is the light cylinder radius, was first introduced by Goldreich & Julian (1969). Even for a current density, ρ_GJ of electrons or ions extracted from the neutron star surface, the space charge ρ<ρ_GJ above the surface since a continuous current density falls off faster with r than ρ_GJ in a dipole field due to field line curvature. Therefore, an electric field, E_Ⅱ, develops parallel to the magnetic field,

in the absence of any other sources of charge (Arons & Scharlemann 1979).

The two main types of polar cap accelerator are vacuum gaps (Ruderman & Sutherland 1975, Usov & Melrose 1995) and space-charge limited flow (SCLF) gaps (Arons & Scharlemann1979, Harding & Muslimov1998). Which of these form in a particular pulsar depends on whether the neutron star surface temperature is high enough to overcome the binding (or cohesive) forces on charged particles due to the lattice structure in a strong magnetic field. If the surface temperature is not high enough, vacuum gaps can form above the surface (Usov & Melrose1995). The surface temperatures of most pulsars (those having surface magnetic fields below ~ 10¹⁴ G) are thought to be high enough that charges are “boiled off ” the surface layers (Medin & Lai 2007) and can flow along the open field lines in SCLF. The E_Ⅱ in steady-state SCLF accelerators is computed using Eq. (1) assuming that ρ(R)=ρ_GJ(R) at the neutron star surface. Since ρ_GJ(r) is modified by inertial frame-dragging (Muslimov & Tsygan1992), E_Ⅱ is significantly larger than it is for flat space.

Acceleration will be self-limited by the development of pair cascades, at altitudes where the particles reach high enough Lorentz factors to radiate γ-ray photons. Electron-positron pair production can occur by single photons in the strong magnetic field of the neutron star (Erber 1966, Daugherty & Harding 1983). Since the photons are initially emitted nearly parallel to the magnetic field, photons need very high energies ε>100 MeV to produce pairs. Such high energies require particle acceleration to Lorentz factors of at least γ~10⁵-10⁷. The pair cascades can be initiated either by curvature radiation (CR) (Daugherty & Harding1982) or by resonant or non-resonant inverse- Compton scattering (ICS) of stellar thermal X-rays by primary electrons (Sturner et al. 1995). The polarization of pairs above the pair formation front (PFF) may short out the E_Ⅱ by reversing a small fraction of the positrons, halting any further acceleration at higher altitude. Recent simulations of timedependent polar cap pair cascades (Timokhin & Arons 2013) have found that, unless the current is very close to ρ_GJ there is no steady solution for gap acceleration and pair production will occur in cyclic bursts on very short timescales (of order the light crossing time in the gap). Pulsars older than ~10⁷ yr and most of the millisecond pulsars cannot produce pair cascades through CR since the E_Ⅱ does not grow fast enough to accelerate particles as the dipole field falls. These pulsars are “pair-starved” and since their E_Ⅱ is unscreened, particles continue to accelerate on all open field lines to high altitude.

Radiated spectra from CR-initiated (Daugherty & Harding1982) and ICS-initiated (Sturner et al. 1995) cascades are hard (power laws with indices 1.5 - 2.0) (Harding & Daugherty 1998) with cutoffs due to magnetic pair production attenuation at energies around several GeV. Since the pair production attenuation coefficient is exponential in photon energy, the spectral cutoffs have a very sharp, “superexponential” shape and are therefore a distinguishable prediction of polar cap models.

Due to the geometry of the field lines and the assumed boundary conditions of the accelerator, the altitude of the PFF varies with magnetic colatitude across the polar cap (Arons 1983, Harding & Muslimov 1998). Near the polar cap rim, which is assumed to be a perfectly conducting boundary, the electric field is decreasing and a larger distance is required for the electrons to accelerate to the Lorentz factor needed to radiate photons energetic enough to produce pairs. The PFF thus curves upward as the boundary is approached, forming a narrow slot gap near the last open field line (Muslimov & Harding 2003). Since E_Ⅱ is unscreened in the slot gap, particles continue to accelerate and radiate to high altitude along the last open field lines (Muslimov & Harding 2004).

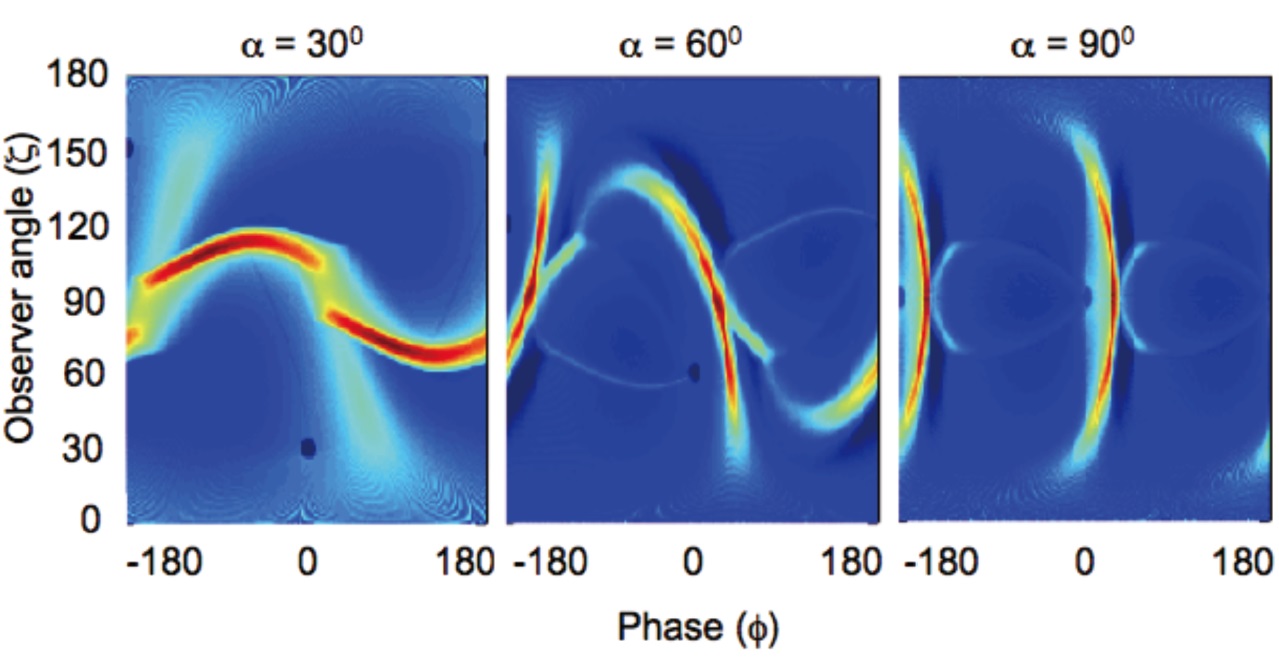
The geometry of emission at high altitude is strongly influenced by special relativistic effects of aberration, timeof- flight and retardation of the magnetic field. Morini (1983) first noted that the combined phase shifts from aberration and time-of-flight, of photons radiated tangent to a magnetic dipole field from the polar cap to the light cylinder, nearly cancel those due to field line curvature on the trailing edge of the open-field region. Radiation along such trailing field lines bunches in phase, forming a sharp emission peak or caustic in the pulse profile (Fig. 1). On the leading side, these phase shifts add up to spread photons emitted at various altitudes over a large range of phases. Most observer angles sweep across caustics from both magnetic poles, resulting in a double-peaked pulse profile where the peaks generally have phase separation less than 180° (Dyks & Rudak 2003). Such profiles are very similar to those of the bright γ-ray pulsars, Crab and Vela. The predicted polarization characteristics of such a “two-pole caustic” (TPC) model in a retarded vacuum dipole (Deutsch 1955) geometry can also explain the observed optical polarization of the Crab pulsar (Dyks et al. 2004). Emission from the slot gap will have a TPC geometry, thus producing similar profiles with caustic peaks. Pair starved polar cap models (PSPC) produce very different emission patterns, with radiation concentrated near the polar caps but extending to high altitude (Venter et al. 2009). The predicted light curves will consist of narrow peaks in phase with the radio pulse if the viewing angle crosses near the magnetic axis, but will consist of a single broad peak leading the radio pulse if the viewing angle to the magnetic axis is large, since the high-altitude emission will be shifted to earlier phase by aberration (Venter et al. 2009).

The electrons that accelerate in the slot gap will radiate curvature, inverse Compton and synchrotron radiation at high altitudes. Initially, their Lorentz factors will be limited

by curvature-radiation reaction (Muslimov & Harding 2004) to γ_CRR=((3/2)E_Ⅱρ_c²/e)^1/4~3×10⁷ and the peak energy of their CR spectrum will be

where

is the electron Compton wavelength and ρ_c is the local field line radius of curvature. As the electrons reach higher altitude, where the local magnetic field has dropped to B~10⁶-10⁸G, they may be able to resonantly absorb radio photons of energy ε_0,GHz that are at the cyclotron resonance in their rest frame (Lyubarski & Petrova 1998). The condition for resonant absorption is γ_R=3×10⁵B₈ε_0,GHz/(1-βμ₀) where B₈≡B/10⁸G and μ₀ is the cosine of the angle between the radio photon and the electron momentum. The electrons are then excited to higher Landau states and radiate synchrotron emission.

With the large and growing populations of γ-ray pulsars, showing a variety of light curve shapes reflecting most likely different viewing geometry, it is now possible to test and constrain emission model geometry. With its increased sensitivity, Fermi has also measured the phase

resolved spectra of bright pulsars with great detail, allowing constraints on the particle acceleration and emission mechanisms.

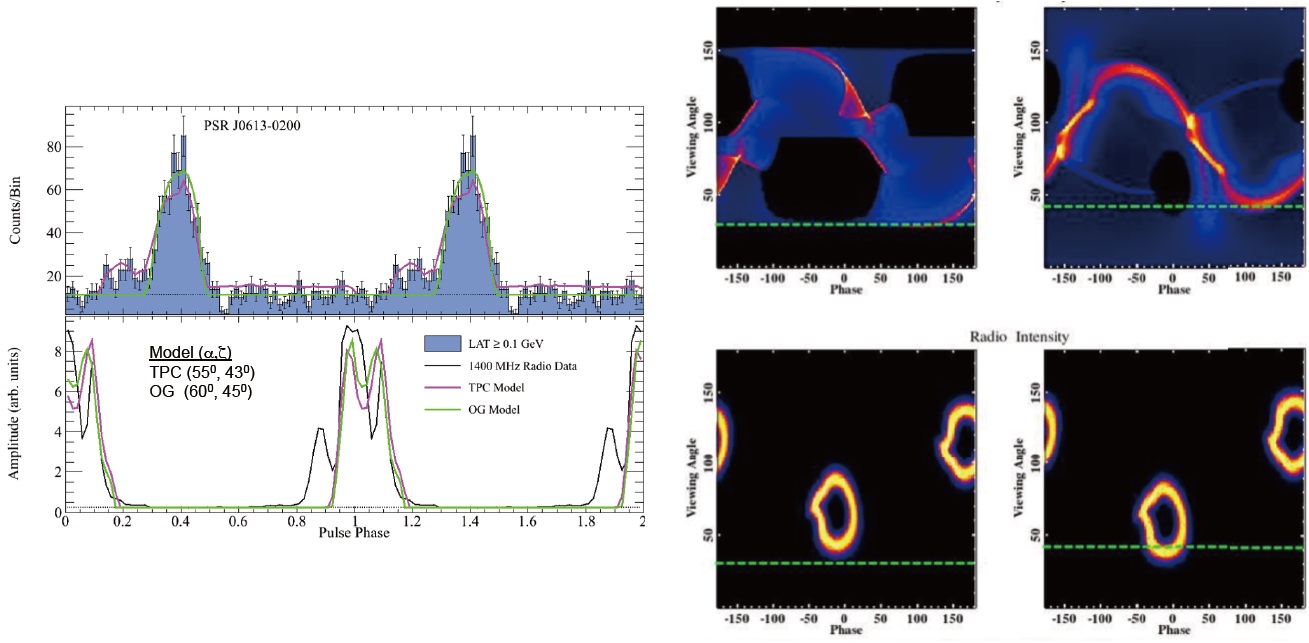
Modeling γ-ray light curves and fitting to Fermi data can provide powerful constraints on acceleration and emission geometry. A method of light curve modeling that has proven very useful is to use geometrical representations of the proposed emission models, such as polar cap (PC), pair-starved polar cap (PSPC), outer gap (OG) and SG (or TPC), parameterized by gap width and maximum emission altitude. Observed pulsar light curves are fit by comparing to model light curve altas' (Watters et al. 2009, Venter et al. 2009) for the full range of magnetic inclination α and observer angle ζ. One then obtains the viewing geometry for each pulsar as well as constraints on gap width and emission altitude and geometry. Fits to the first eight γ-ray MSP light curves detected by Fermi (Abdo et al. 2009c) by Venter et al. (2009) with SG, OG and PSPC geometrical models in a retarded vacuum magnetosphere found that six are well fit by OG or SG and two by PSPC models. Thus, most MSPs must have narrow gaps, similar to those of young pulsars, that require screening by pair cascades. This result was not expected given their very weak fields (Harding et al. 2005), implying perhaps non-dipolar magnetic field structure (Harding & Muslimov 2011a,b).

Nineteen γ-ray and radio MSP light curves in the first Fermi Pulsar Catalog (Abdo et al. 2010a) and 40 in the Second Fermi Pulsar Catalog (Abdo et al. 2013) were fit by Johnson (2012) and Johnson et al. (2013) respectively. These studies identified three classes of MSP light curves. Class I have γ-ray peaks, fit by standard SG or OG models, that lag in phase the main radio peak, fit by lower-altitude cone beams centered on the magnetic poles. Class II MSPs have aligned γ-ray and radio profiles, both fit with altitude-limited SG or OG models so that the radio peaks are caustics as well as the γ-ray peaks (Venter et al. 2012). Class III MSPs have γ-ray peaks, fit by PSPC models, that lead in phase the radio peak(s), fit by cone beams. In the Second Fermi Pulsar Catalog, there are 26 Class I, 6 Class II and 6 Class III MSPs. An example of a Class I MSP is shown in Fig. 2. There is only one (out of 77) Class II normal γ-ray pulsar (the Crab pulsar), so light curves with aligned radio and γ-ray profiles are much more common among MSPs, and there are no clear examples of Class III normal γ-ray pulsars. Of the Class I MSPs, roughly half are better fit with SG models and half with OG models. The SG/OG geometry tends to better fit the light curves having a higher/lower level of off-peak emission, which requires emission below the null charge surface.

Pierbattista et al. (2013) have fit all the γ-ray and radio light curves of normal (non-recycled) radio-loud (RL) pulsars and the γ-ray light curves of normal radio-quiet (RQ) pulsars of the Second Fermi Pulsar Catalog. They used PC, SG and OG geometry to model the γ-ray light curves and cone beams to model the radio light curves. Of the RL pulsars, 8% best fit PC models, 56% best fit SG models and 36% best fit OG models. Of the RQ pulsars, 19% best fit PC, 33% fit SG and 48% fit OG. These results and the fits to MSP light curves suggest that neither the SG and OG geometries are right by themselves and that the true emission is some hybrid of the two geometries. Thus, at certain viewing angles the lower altitude emission is weak but at other angles we see the emission more equally distributed between high and low altitudes.

Light curve modeling can also be used to constrain magnetic field structure. Until recently, the retarded vacuum dipole was the only geometry used to model high-energy pulsar light curves, but in the last few years, solutions for the force-free magnetosphere (Spitkovsky 2006, Timokhin 2006), which enforces the E·B=0 condition everywhere, and magnetospheres with finite conductivity (Kalapotharakos et al. 2012a) have been computed. Such geometries are thought to be closer to the magnetospheric geometry of a young pulsar in which pair cascades screen the E_Ⅱ throughout most of the open field volume except in small or narrow chargedepleted regions. The first light curve models using forcefree geometry (Bai & Spitkovsky 2010) show that the caustic patterns are somewhat different from those in vacuum dipole geometry. Harding et al. (2011) showed that the peaks of SG and OG profiles computed in force-free magnetospheres were shifted to later phase compared to those in vacuum magnetic dipole geometry. The tighter sweepback of field lines near the light cylinder produces a greater shift of the open field volume to later phase in force-free models. Fits of the Vela profile showed that the force-free light curves have a phase lag with the radio pulse much larger than observed. Light curves computed in magnetospheres with finite conductivity, which lie between vacuum and force-free magnetospheres, have peaks that move to later phase with increasing conductivity (Kalapotharakos et al. 2012b). Radio phase lags are thus a good diagnostic of magnetospheric structure.

Determining whether pulsar spectral cutoffs are simple or super-exponentials could confirm or rule out γ-ray emission in the strong near-surface magnetic fields predicted by PC models. Within the first few months of data collection, Fermi measurement of the spectra cutoff of Vela (Abdo 2009a) was able to rule out the super-exponential fit with a significance of 16σ. The cutoffs of other bright pulsar spectra such as Geminga (Abdo 2010d) and the Crab (Abdo et al. 2010c) also fit a simple exponential shape, indicating that the γ-rays are emitted far above the neutron star surface. In fact, the fits even prefer a shape that is more gradual than a simple exponential.

Measurements of the pulsar spectra across the pulse profile in small phase bins is revealing new details about the emission. Both the photon index and particularly the cutoff energy vary with phase. The cutoff energy, E_c, undergoes rapid changes in the peaks and in the interpeak region, in the case of Vela (Abdo 2010b), by factors of 2 - 3. Such changes in cutoff energy can account for the gradual shape of the phase-average spectra and also indicate rapid changes in characteristics affecting the radiation, such as altitude or magnetic field line curvature. In most outer magnetosphere models, the accelerating particles are radiation-reaction limited (i.e. their rate of energy gain from acceleration is balanced by their curvature radiation losses). The cutoff values roughly agree with those predicted for curvature radiation (Eq. (2)) in the outer magnetosphere since the E_Ⅱ is similar for SG and OG models. So, the variation in E_c with phase would reflect variations in radius of curvature, E_Ⅱ or both. Decesar et al. (2013) have used the light curve fits, that give curvature and emission radii as a function of phase, and phase-resolved spectra of four bright pulsars to estimate E_Ⅱ, assuming E_c = E_CR in Eq. (2). They found that the E_Ⅱ needed to produce the measured Ec in vacuum magnetospheres is larger than the local B field, which is not physical. However, force-free magnetospheres allow E_Ⅱ<B since the curvature radii are much larger than for the vacuum dipole, because currents straighten the poloidal field lines.

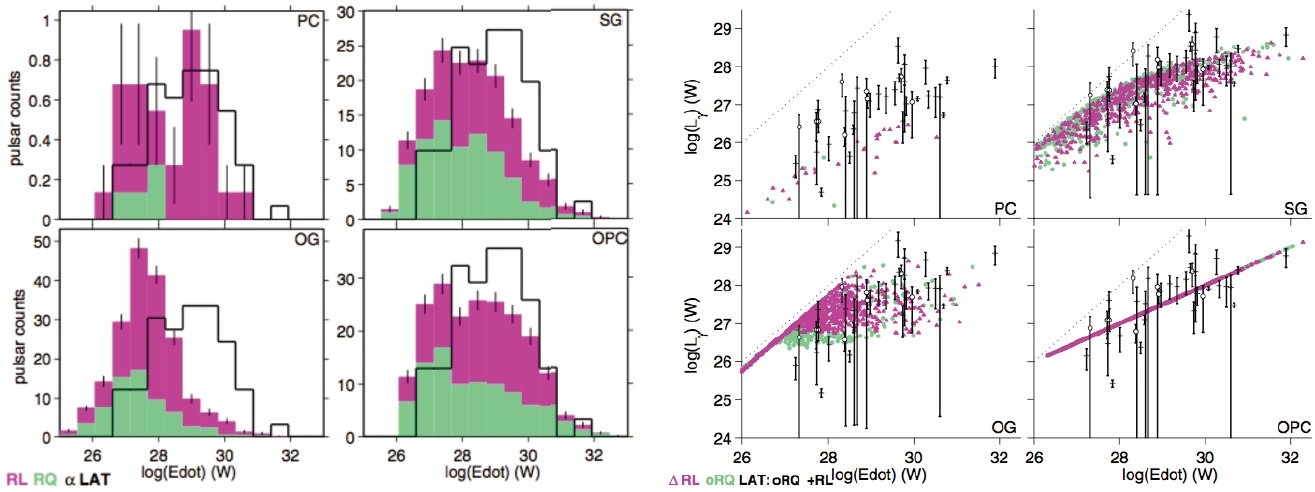
With the much larger population of detected γ-ray pulsars, both radio-loud and radio-weak, population synthesis becomes a more powerful tool for comparing the distributions of various properties with those predicted by models (e.g. Watter & Romani 2011). If the different emission models such as SG, OG or PC models predict distinct distributions of measurable γ-ray pulsar properties, such as age, spin-down luminosity, γ-ray vs. spin-down luminosity, light curve peak separations and radio lags, then observed distributions will distinguish between these models or constrain their parameters. Pierbattista et al. (2012) have simulated a population of normal isolated γ-ray and radio pulsars and compared the characteristics predicted in PC, SG and OG models with those of objects in the first Fermi Pulsar Catalog. Two examples, shown in Fig. 3, are the distribution

of RL and RQ pulsars in ？ and γ-ray luminosity L_γ vs. ？. These results show that none of the models produce the numbers or the high luminosities of the young, energetic pulsars, although the SG and OG models can produce the trend and spread in L_γ vs. ？.