The hybrid-type mount combines a passive mounting device with active technology, thus representing a new alternative for high-tech facilities, automobiles, ships, and the like. The hybrid type, which can be activated by various types of actuators including hydraulic actuators (Turnip et al., 2009), electromagnetic actuators (Howard et al., 2000; Lee and Lee, 2009) or piezoelectric actuators (Kamada et al., 1997; Choi et al., 2004; Nguyen et al., 2009), is utilized to improve the isolation performance of the passive type. In our previous research (Moon et al., 2010; Nguyen et al., 2008), a 100 kg-class hybrid mount-combined with a rubber mount and piezostack actuators ？ was developed for use with various items of shipboard machinery installed on naval ships.

This research is focused on a novel hybrid mount capable of supporting a static load of 500 kg. The hybrid mount requires better performance against both shock and vibration loading, since the mount is designed for installation on the shipboard equipment of naval ships. So far, several configurations of hybrid mounts utilizing piezostack actuators have been designed on the basis of three types: serial (Kamada et al., 1997; Ichchou et al., 2001), parallel (Huang et al., 2003; Yang et al., 2001), and inertial types (Burdisso and Heilmann, 1998; Benassi and Elliott, 2005). The piezostack actuator generally has such a high degree of stiffness that the parallel type is not suitable for the hybrid mount to be developed. The serial type, which makes use of piezostack actuators, however, does not take advantage of the high actuating force property because the stroke of a piezostack actuator is very small. On the other hand, the inertia type is appropriate for a new type of hybrid mount requiring high actuating force over a wide frequency range, although the generable actuating force is also relatively low at low frequency excitations.

The main technical contribution of this study is to introduce a new hybrid mount which is very effective for vibration control in broadband frequency range. Especially, the new hybrid mount was designed based on military specifications which are normally used for the performance evaluation of the standard resilient passive rubber mounts of US Navy. While the hybrid mount studied in the previous research was a serial-type mount designed for serial connection with the rubber and piezostack actuators, the new hybrid mount was designed as an inertia-type mount in order to generate greater control force. The new hybrid mount consists of a commercial rubber resilient mount, a piezostack actuator, and an inertial mass. The rubber mount is one of the US Navy’s standard resilient mounts (passive type) (Howard et al., 2000). In order to evaluate the various performances of the hybrid mount, several experimental tests were carried out according to military specifications. In addition, control performance based on the concept of vibration transmissibility was tested using a special model capable of simulating the double mounting system. Through a series of experimental tests, it has been confirmed that the hybrid mount delivers good performance against both vibration and shock, making it suitable for use in naval ships.

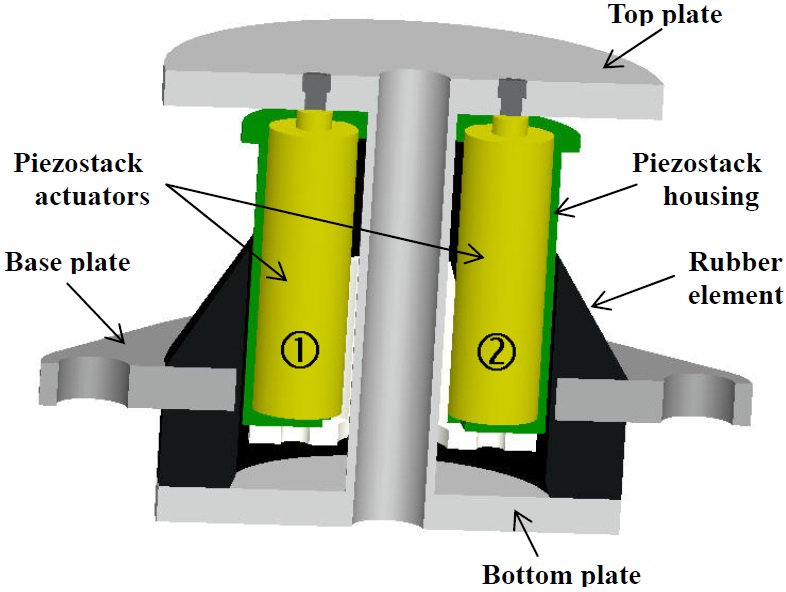
The hybrid mount proposed in this study consists of passive and active elements, with a rubber element serving as the passive element and a piezostack element serving as the active one, following the extended line of the previous research (Moon et al., 2010). The hybrid mount developed in the previous research was composed of a rubber element and two piezostack elements, which were serially connected as shown in Fig. 1. The two piezostack actuators were inserted into the rubber element in order to meet the height constraint. The mount had a natural frequency of 6.3 Hz and a rated load of 100 kg.

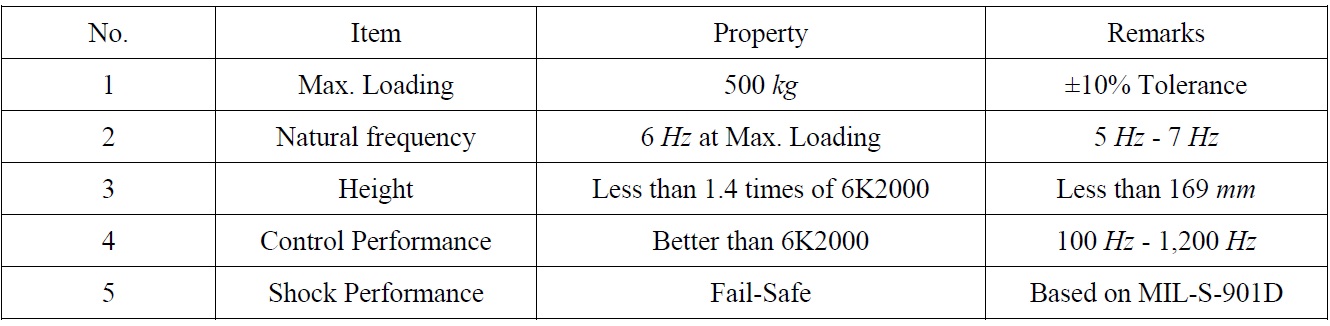
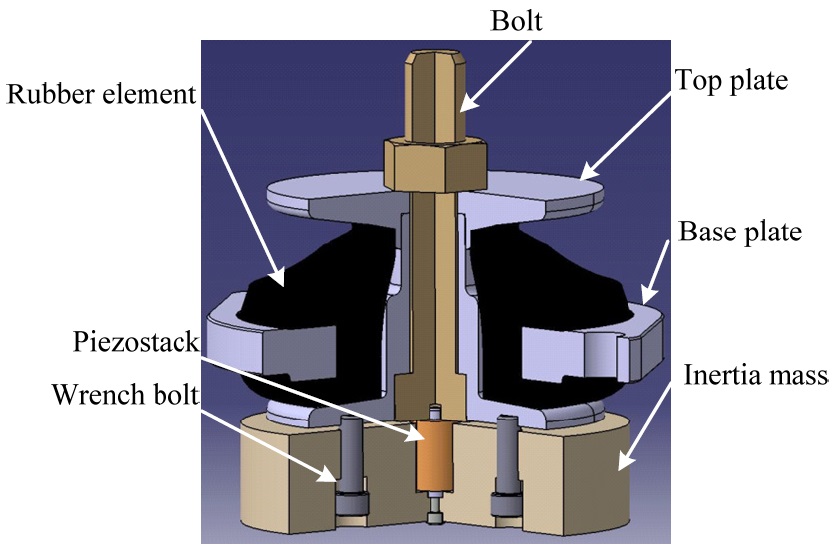
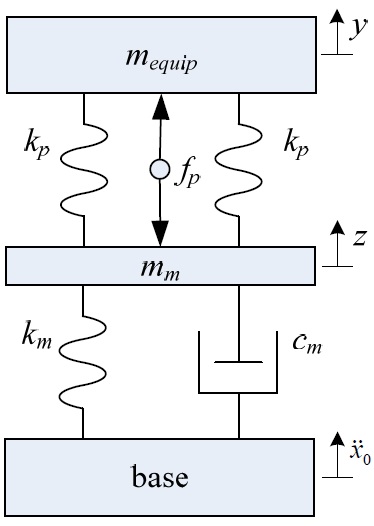
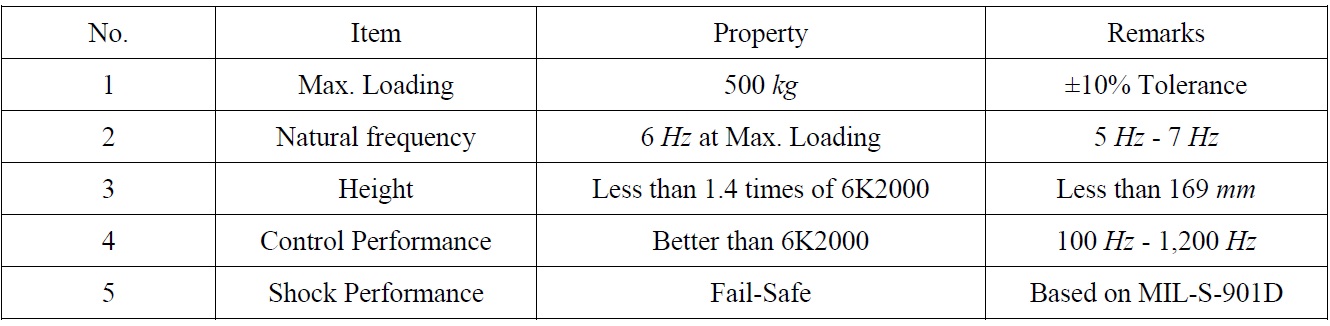
The design requirements of the new hybrid mount are summarized in Table 1. Since the new hybrid mount should have greater static capability than the serial-type hybrid mount, greater control force was required to obtain a good control performance. However, the control force of commercial piezostack actuators is limited in terms of their height and volume, and large piezostack actuators are both rare and extremely expensivee serial-type hybrid mount developed in the previous research was inappropriate for a large hybrid mount, a new inertia-type hybrid mount was proposed, as shown in Fig. 2. The proposed hybrid mount consists of a commercial navy mount (model 6K2000), a piezostack actuator, and an inertial mass. The inertial mass is hung down from the piezostack actuator, and the piezostack actuator is connected to the equipment with a rigid bolting shaft. Although the control force is proportional to the weight of the inertial mass, the height of the inertial mass is restricted to the design requirements given in Table 1.

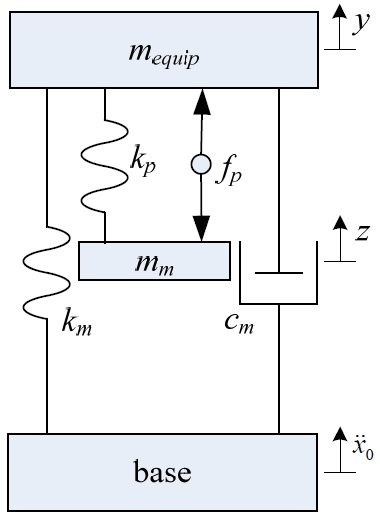
Fig. 3 and Fig. 4 show schematically lumped-mass models of the proposed inertia-type hybrid mount and the serial-type hybrid mount, respectively. The vibration system, consisting of the proposed hybrid mount and equipment, can be modeled as a two degree-of-freedom (2-DOF) system, as shown in Fig. 3. From the model, the governing equations of motion can be derived as follows:

where z(t) and y(t) are the relative displacement of the inertial mass m_m = 10 kg, and of the equipment m_equip = 500 kg, respectively, to base displacement; ？₀(t) is the acceleration of the base (excitation); k_m = 0.86 MN/m and c_m = 2.8 kNm/s are the stiffness and damping coefficients of the rubber element, respectively; k_p = 600 MN/m is the stiffness of the piezostack actuator; and f_p(t) is the force exerted by the piezostack actuators. On the other hand, the governing equations of motion of the serial-type hybrid mount (as shown in Fig. 4) can be expressed as follows:

where z(t) is the relative displacement of the intermediate mass m_m = 0.5 kg to base displacement. As shown in Fig. 3, there is a piezostack housing between the piezostack actuators and the rubber element. Since the housing is connected with the piezostack actuators, it could be modeled as the intermediate mass. To model the two hybrid mounts, the dynamic characteristics of the rubber element were experimentally obtained. First, the rubber element was tested and identified based on the 1-DOF theory. The stiffness of the rubber element was determined from the resonant frequency under a load. The damping ratio of the rubber element was obtained by using the half-power bandwidth method. Next, the dynamic stiffness of the piezostack actuators was taken from the product catalogue (Piezomechaniks, 2011).

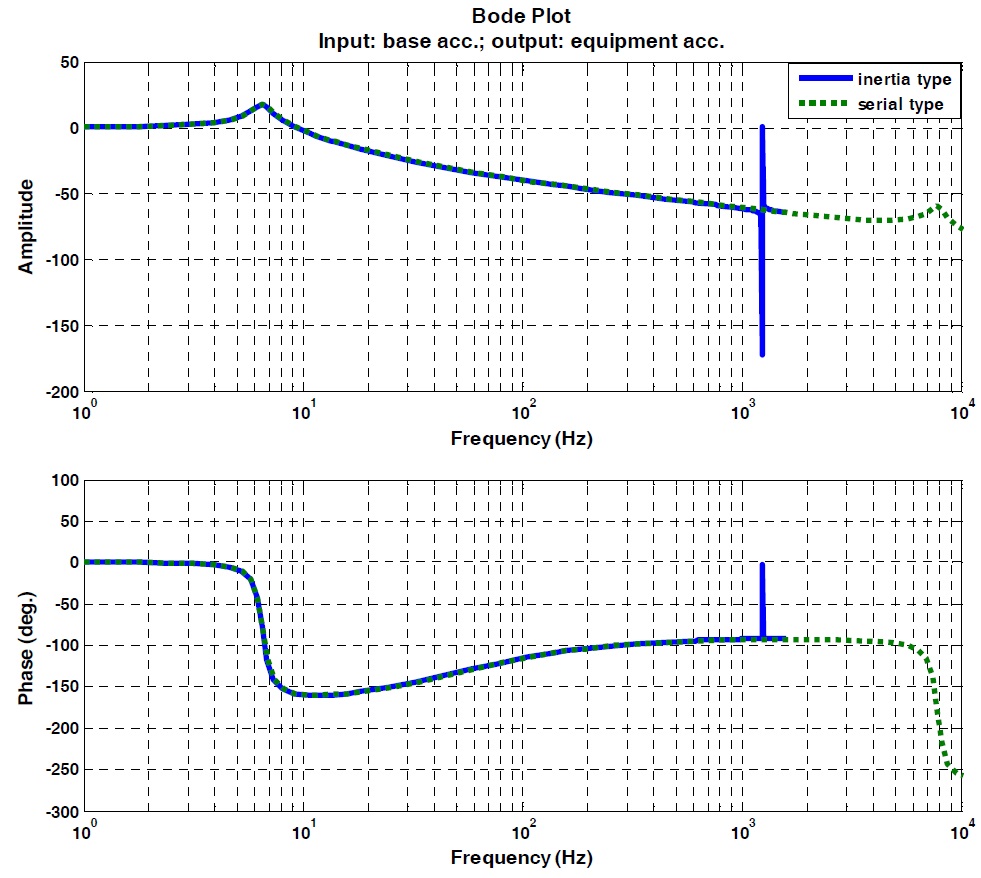
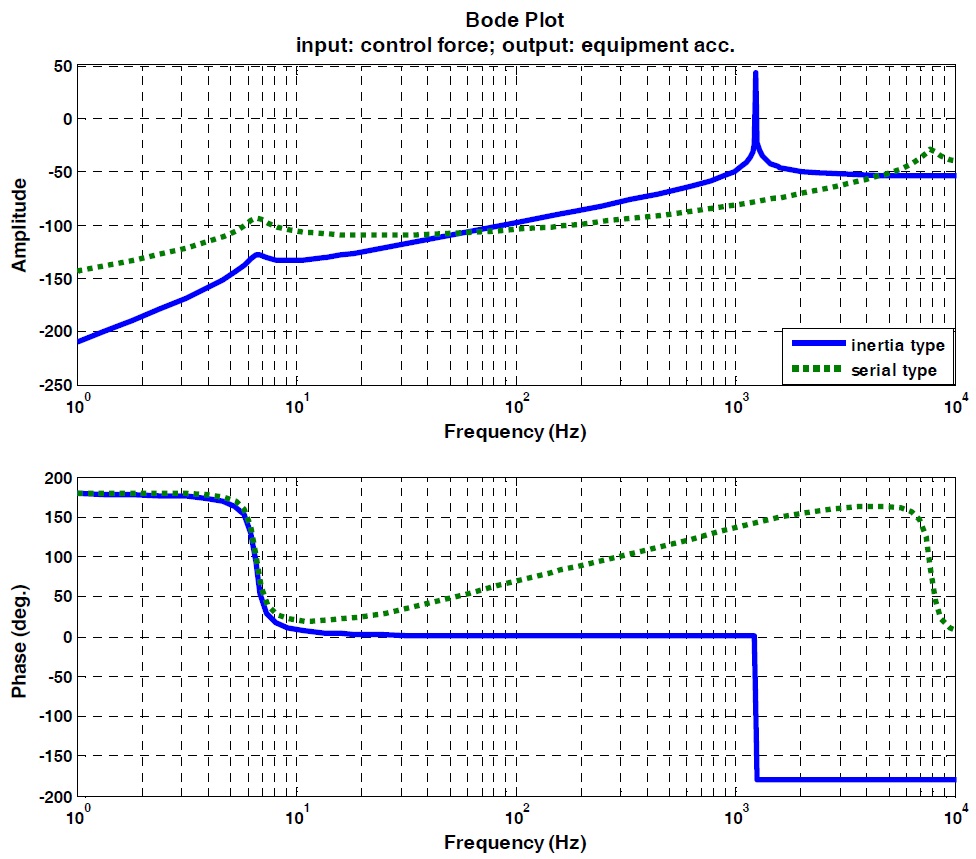
Fig. 5 and Fig. 6 show the Bode plots from base exciting acceleration to equipment acceleration, and from piezostack actuating control force to equipment acceleration, respectively. Both figures were plotted using the results based on Eqs. (1) - (4). As shown in Fig. 5, the two Bode plots have the same characteristics below 1,200 Hz. It was observed that there were two resonant peaks from the rubber and the piezostack, but they did not fall within the specified frequency range from 100 Hz to 1,200 Hz. As shown in Fig. 6, the control force of the inertia-type hybrid mount was well transmitted to the equipment, compared to the serial-type hybrid mount, in the specified frequency range. In the case of the serial-type hybrid mount,ol force was generated from the two piezostack actuators. It should be noted that the inertia-type hybrid mount has only one piezostack actuator; and, since it shows flat phase characteristics, active performance can be easily controlled.

The proposed hybrid mount consists of a commercial navy mount (model: 6K2000 produced by Super Century, Co. (2011)), a piezostack actuator, and an inertial mass. The commercial navy mount developed according to the military specification MILM- 17508F(SH) (1990) was slightly modified in order to connect it with the piezostack actuator using an M8 bolt. It is assumed

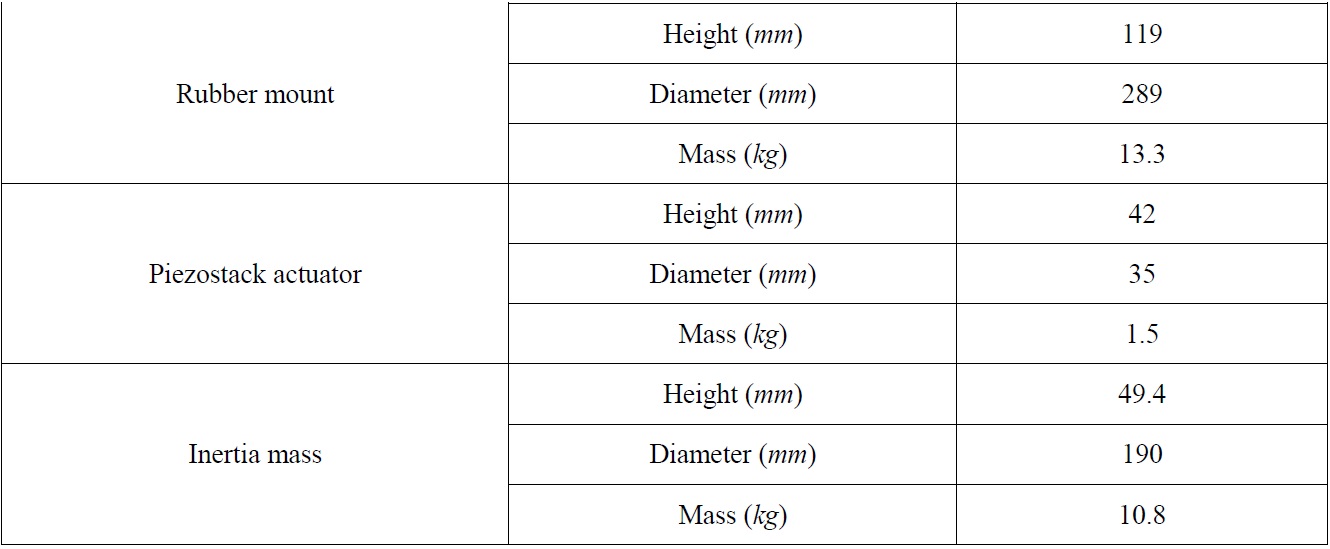
that this minor modification would not affect the performance of the mount. The piezostack was purchased from Piezomechaniks GmbH (model: PSt350bp/25/15VS35) (2011). Considering the height constraint included among the design requirements summarized in Table 1, the inertial mass (fabricated from mild steel) was determined to have a weight of 10.8 kg. The inertial mass was connected with the piezostack actuator with an M6 bolt. The hybrid mount has to have incorporated into its design certain “captive features” to prevential mass from coming free in the event of a failure of the rubber element due to a high impact shock or simply under normal service conditions according to MIL-M-17185A(SHIPS) (1956). For this purpose, four wrench bolts were inserted between the 6K2000 andial mass. The wrench bolts have no screw, and were not connected tightly. Fig. 7 shows a photograph of the prototype hybrid mount, and Table 2 shows the dimension and mass of each component of the proposed hybrid mount.

The fabricated hybrid mounts were experimentally tested to confirm the required performance. It is known that there are no specific military specifications for the hybrid mounts for use on naval vessels. As a tough measure, both MIL-M-17185A (SHIPS) and MIL-M-17508F(SH) were optionally applied to the military performance evaluation for the developed hybrid mount, since the hybrid mount was developed based on the resilient 6K2000 mount. The military performance tests included the following: resonant frequency, deflection at rated load, quality of the rubber to metal bond, strength test in the axial direction, strength test in the radial direction, drift test, fatigue test, and shock test. Since these testing items are the same as those used in the previous research (Moon et al., 2010), the test results were only addressed briefly in this paper.

Fig. 8 shows the apparatus used to measure the resonant frequencies of the mount directly. A test weight of 500 kg was applied to the mount. The system was excited with a hydraulic shaker and some accelerometers were attached to the shaking table. The top of the mount using swept sinusoidal vibration with a sweep rate low enough to achieve a quasi-steady-state response. The test was conducted on ten hybrid mounts. It is found out that the resonant frequencies are in the range of 6.4 Hz - 6.9 Hz at a rated load of 500 kg.

MIL-M-17508F(SH) states that the deflections of the hybrid mount, when tested in the axial direction at their respective rated loads, should be within the specified limit of 10.2 mm - 17.2 mm and should not show any break or separation between the component parts. This test was conducted on eight hybrid mounts using a hydraulic actuator, as shown in Fig. 9. Each mount was subjected to a single loading cycle in the axial direction. The deflection at the rated load was measured as ranging from 15.9 mm to 17.0 mm.

MIL-M-17508F(SH) states that mounts should show no breaks, cracks, or tears in the rubber elements, or any evidence of delamination at the rubber to metal bond interfaces. The load on the mounts was increased to two times the upper rated load after recording the degree of deflection under the upper rated load. The mount held twice its upper rated load, and the appearance of the rubber element and of the rubber-to-metal bond was examined to determine conformance. No damage was observed.

MIL-M-17508F(SH) states that mounts, when tested in the axial direction, should not show any separation or break between the parts, nor any permanent deformation of the metal parts in excess of 0.794 mm (= 1/32 inch). The mount was secured in a suitable jig and subjected to four cycles, loadings and unloadings, in the axial direction. The specified loads mentioned in the military specifications were applied to the mount. The mount was inspected during and after testing for any break or separation in the rubber or between the rubber and the metal parts, as well as for deformation of the metal parts. No breaks or separations were observed.

MIL-M-17508F(SH) states that mounts, when tested in the radial direction, should not show any separation or break between the parts nor any permanent deformation of the metal parts in excess of 0.794 mm (= 1/32 inch). Two mounts were secured by a suitable jig and tested for compressive strength in the radial direction. The mount was subjected to four cycles, loadings and unloadings, in the radial direction. Each mount was compressed axially to that amount at which its upper rated load rating deflected the mount during the test for deflection under the rated load in the axial direction, as shown in Fig. 10. The specified loads mentioned in the military specifications were applied to the mounts. No breaks or separations were observed.

The height of the mount was measured one hour after loading and again after 96 hours. The difference in the two readings was taken as the drift of the mount. The drift limit was set at 2.03 mm, and the drift of the hybrid mounts were found to be 1.83 mm and 1.98 mm. The mount was tested again for resonant frequency at its upper rated load. At the end of testing, the resonant frequency of the mount was observed not to have exceeded 15% changing difference.

Mounts should be able to withstand fatigue loading without showing any signs of failure or deterioration in the rubber element, the rubber to metal bond, or the metal components according to MIL-M-17508F(SH). Each mount was loaded to its upper rated load in the axial direction and subjected to 500,000 cycles of vibration at its natural frequency, with mount deflecttion of ±1.27 mm (= 0.050 inch), using a hydraulic actuator, as shown in Fig. 9. No breaks or separations were observed.

MIL-M-17185(SHIPS) states that the mount should be of such design that under the hammer blows of the applicable shock test. No separation, or break in/or between components of the mount shall occur which will permit the mounted equipment to become free. The natural frequency of the mount after the shock test in the axial and radial direction should not vary more than ±15% from the average resonant frequency. The hybrid mounts were tested four at a time on the medium weight shock test machine. A dummy mass of about 2,000 kg was loaded onto the four mounts, as shown in Fig. 11. Tests were conducted in the axial and radial directions, employing the testing apparatus. The hammer blows were applied at the intensity and in the number specified for groups II and III for medium weight equipment under specification MIL-S-901D (1989). Actually, three blows at the maximum hammer drop height of 1.67 m were applied to each group. The weight of the hammer is about 1,356 kg. No damage to the mounts and the dummy mass was observed.

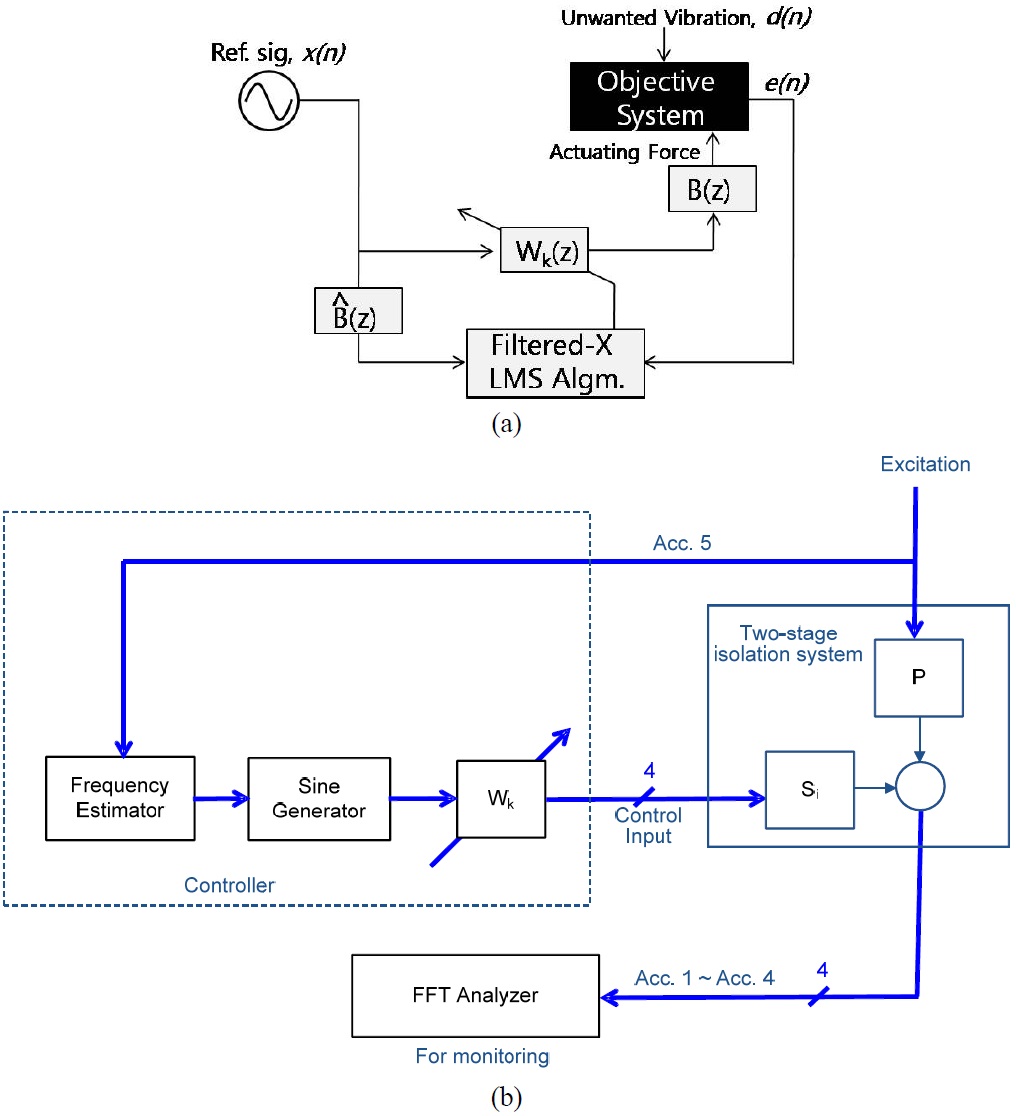
A filtered-X LMS algorithm is an adaptive filter algorithm, which is suitable for active control application (Widrow and Stearns, 1985; Hakansson et al., 1998). It is a feed-forward control which involves canceling disturbance from the system’s response with the reference input(s). In this study, the algorithm was adapted using the feed-forward signals measured on the dummy weight, which was vibrated by an exciter. Items of shipboard equipment generally have self-exciting sources, and they have steady-state characteristics with constant frequencies. Vibration from the equipment is transmitted to the hull of ship through the foundations of equations - such as the mount, damper, steel block, etc. The feed-forward signal measured can be handled as reference input(s) in the control algorithm. The disturbance - in this case, the vibration on each hybrid mount induced by the vibration of the dummy weight, - would be cancelled by first passing the reference input though a filter whose parameters are adjusted by the LMS algorithm.

Fig. 12(a) shows the block diagram of the filtered-X algorithm including the elimination of disturbance with an adaptive finite impulse response (FIR) filter controller. The error ε(n) is expressed as follows:

where d (n) is disturbance; y (n) is the FIR filter’s output; b_k and w_k are the coefficients of the actuator transfer function B and the FIR filter W, respectively; x (n) is the reference input; B, W and X denote

The adaptive algorithm should have an objective function to minimize the adjustment of the variables used in the function. In this study, the least-mean-square (LMS) of the error was used as an objective function, as described in

The mean-square error is a quadratic function of W. The adaptive algorithm adjusts the coefficients of FIR filter, w_k, until the optimal values are achieved at every time step to minimize the objective function. One of the well-known algorithms for achieving this minimum is the method of steepest descent, which may be written as

where μ is a constant of the step size, which regulates the speed and stability of the adaptation process as well as the noise in the weight vector. The noise was attenuated by the adaptive process, which acts like a notch filter. ∇_k is the gradient of the mean-square error, as shown in Eq. (7), and can be written as

As with Eq. (9), the optimal solution, Eq. (8), becomes

In Eq. (10), X_kb_k could not be achieved from the real actuator output, so the estimated actuator transfer function was used.

Fig. 12(b) shows a block diagram representing the application of the filtered-x LMS algorithm to the hybrid mount system. The measured acceleration signal on the payload was defined as the error signal, and a sine function was used as the reference signal. The order of the FIR filter, W_k, was defined as 20, and the estimated actuator transfer function was assumed to be a unit vector. The actuating command signal was computed and adapted to minimize the measured error and was applied to the piezostack actuator through the amplifier as voltage input.

The evaluation of the active control performance for the hybrid mount was processed based on the vibration transmissibility concept, wherein vibration transmissibility is expressed as follows:

In Eq. (11), T_dB is the vibration transmissibility in decibels (dB); and A_M and A_B are the equipment acceleration and the base acceleration, respectively. In this research, a hybrid mount with a controlled condition, which means the piezostack is working, was compared with a 6K2000 passive mount by means of transmissibility. Figure 13 shows the experimental apparatus using an electromagnetic exciter (model: LDS V555) for vibration transmissibility. A dummy weight of 500 kg was installed on the top of the proposed hybrid mount. Two accelerometers were installed on the base block and the dummy weight to measure the output and input accelerations, respectively. By exciting the system vertically from the dummy weight with sinesweeping, vibration transmissibility to the base block can be achieved experimentally from the measured accelerations. Under the controlled condition, a filtered-X LMS control algorithm was adapted to drive the piezostack actuators.

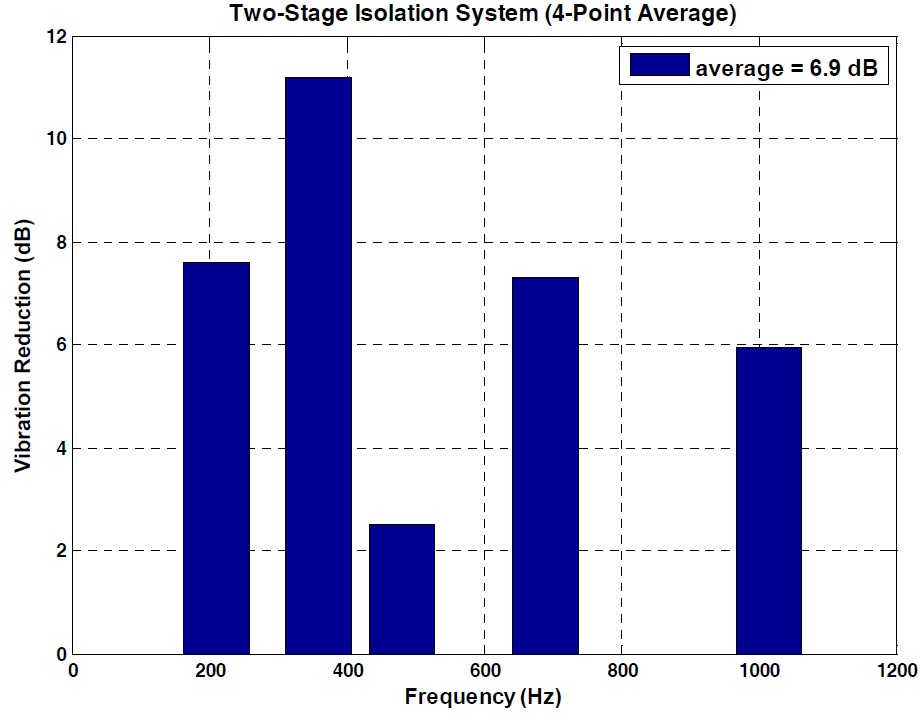
To evaluate the control performance, an experiment in which the excitation ranged from 100 Hz to 1,200 Hz was conducted to evaluate the control performance. The levels of vibration transmissibility with respect to frequency were plotted in Fig. 14. As shown in Fig. 14, the vibration suppression performance was enhanced by about 13 dB on average, in the range of 100 Hz - 1,200 Hz, compared to the 6K2000. The proposed hybrid mount shows greater control performance in the high frequency region. It is because the piezostack actuator has inherently better dynamic characteristics in high frequency region. From these results, it was confirmed that vibration control performance can be significantly improved by activating the piezostack actuators.

System modeling

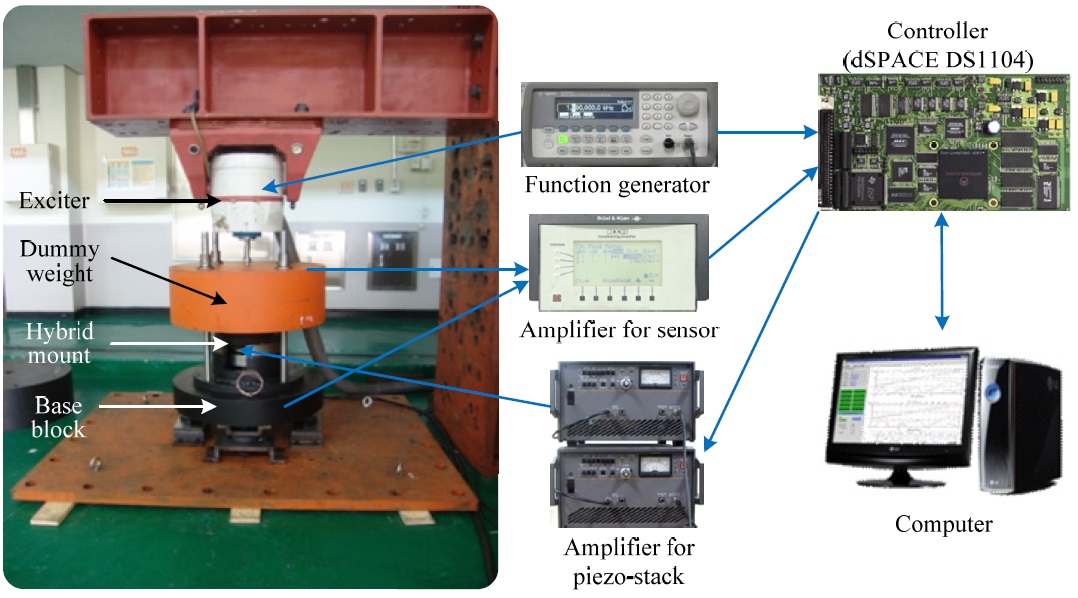
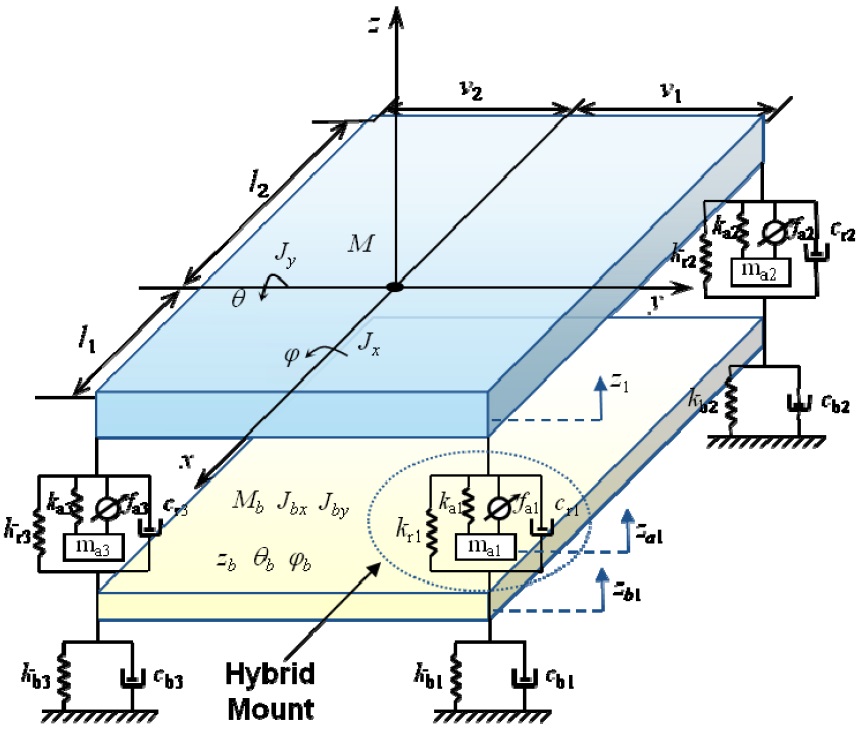
Generally, an isolation system for shipboard equipment consists of four mounts and auxiliary devices. In order to systematically evaluate the active control performance of the proposed hybrid mount, a two-stage isolation system was analytically configured, as shown in Fig. 15. A dummy weight of about 2,000 kg, designed to represent the shipboard equipment, with dimensions of 600 mm × 600 mm × 15 mm (W × D × H), was installed on the top of the upper mount system with the four proposed hybrid mounts. The piezostack actuator at each hybrid mount provided the control force to the dummy weight, and the proper control force could be calculated via digital signal processing using the incoming signals from several sensitive acelerometers installed in a lower location on each hybrid mount. A single intermediate plate was set up between the upper mount system and the lower mount system with four other passive mounts, and assumed as a rigid block.

Fig. 16 presents the mathematical model of the proposed hybrid mount system. The dummy weight and the intermediate plate are assumed as rigid. Each upper mount has an inertial mass of m_a1 ~ m_a4, a piezostack stiffness of k_a1 ~ k_a4, rubber stiffness of k_r1 ~ k_r4, and rubber damping of c_r1 ~ c_r4. Each lower passive mount is expressed as a combination of spring (k_b1 ~ k_b4) and dashpot (c_b1 ~ c_b4) elements. The subscript letters in the parameters, i.e., _a, _r, and b, represent inertial mass, lower rubber mount, and base block, respectively. In this study, the dummy weight is assumed to be excited only vertically.

Therefore, the three DOFs - namely, heaving, rolling and pitching - of the two-stage isolation system were considered, and their motions on the dummy weight can be expressed as the following equations:

where M is the mass of the dummy weight, and z is the vertical displacement at the mass center. J_x and J_y are the polar moment of inertia, and ？ and θ are angular displacements at the mass center. M_x, M_y, and F_e are external moments and force. z_i, ν_i, and l_i are the displacement at point i, rolling moment arm length, and pitching moment arm length, respectively. The equation of motion on the base block may be derived in a similar way to the dummy weight.

where M_b is the mass of the base block, and z_b is the vertical displacement. J_bx and J_by are the polar moment of inertia, and ？_b and θ_b are angular displacements (rolling and pitching). The equation of motion of the inertial mass at the i -th hybrid mount can be derived as follows:

Because the table plate was rigid, the following equations can be induced according to the geometric condition.

By substituting Eq. (19) into Eqs. (12) - (18), the equation of motions in matrix form can be obtained as follows:

where M, C and K are the mass, damping and stiffness matrices, respectively; f_a is the supplemental force vector exerted by the piezostack actuators; f_e is the external force (or moment) vector; E and G are the matrices which define the location of the supplemental force and the external force, respectively; and p is the displacement vector.

Experimental set-up

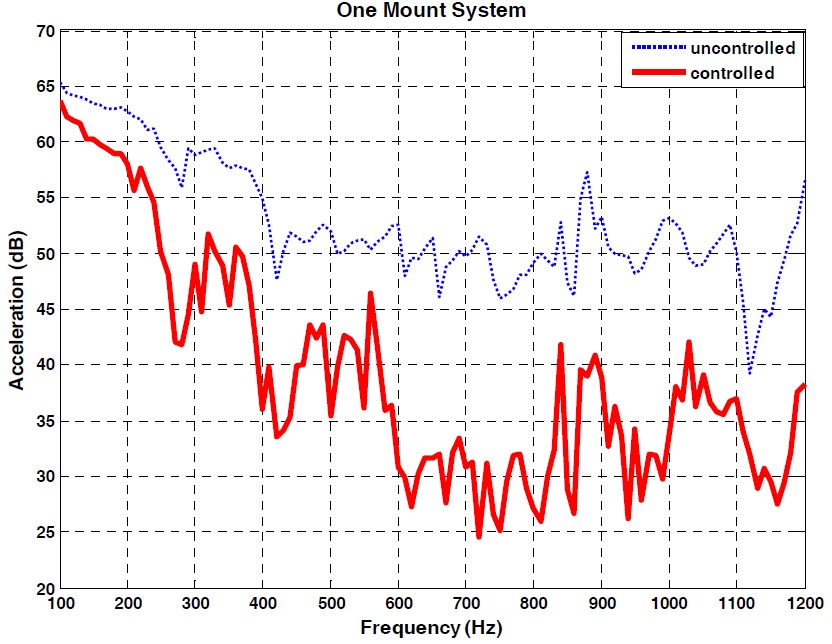
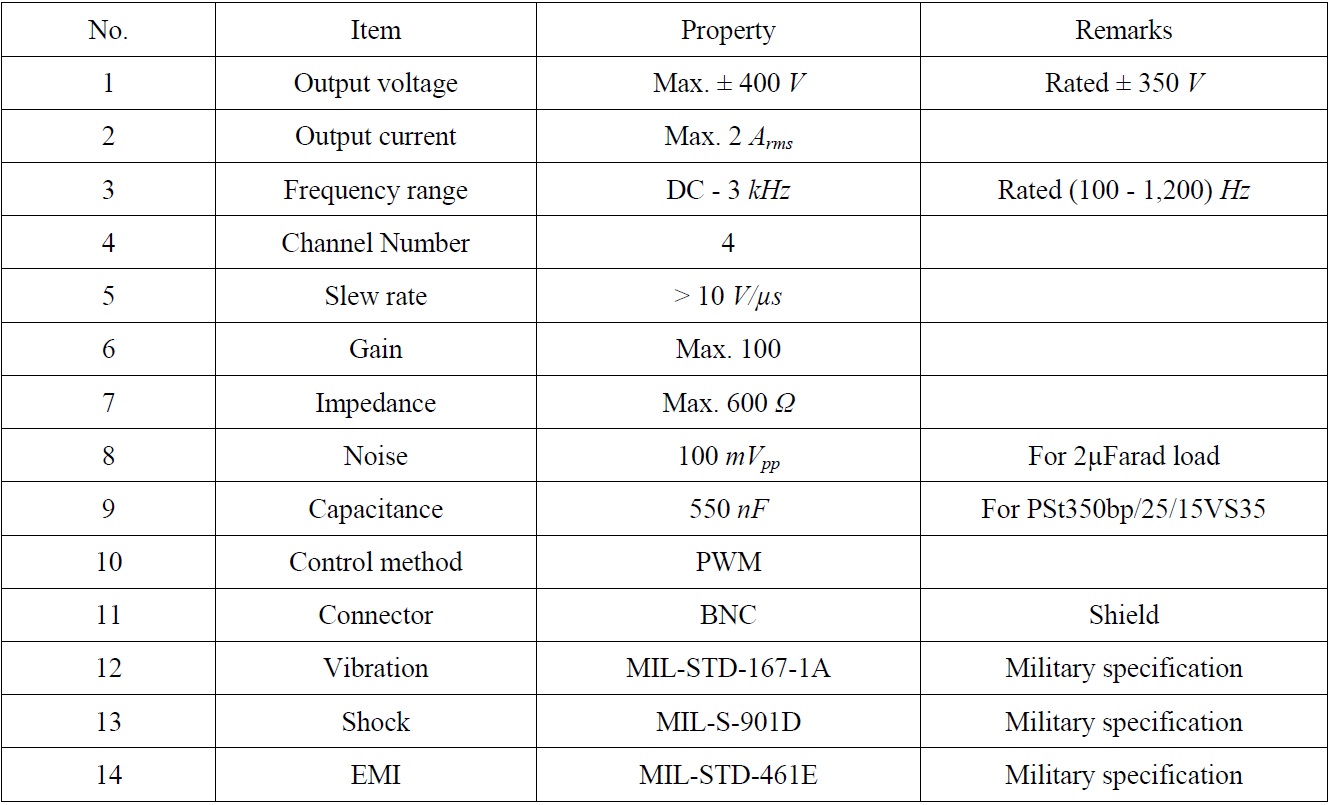
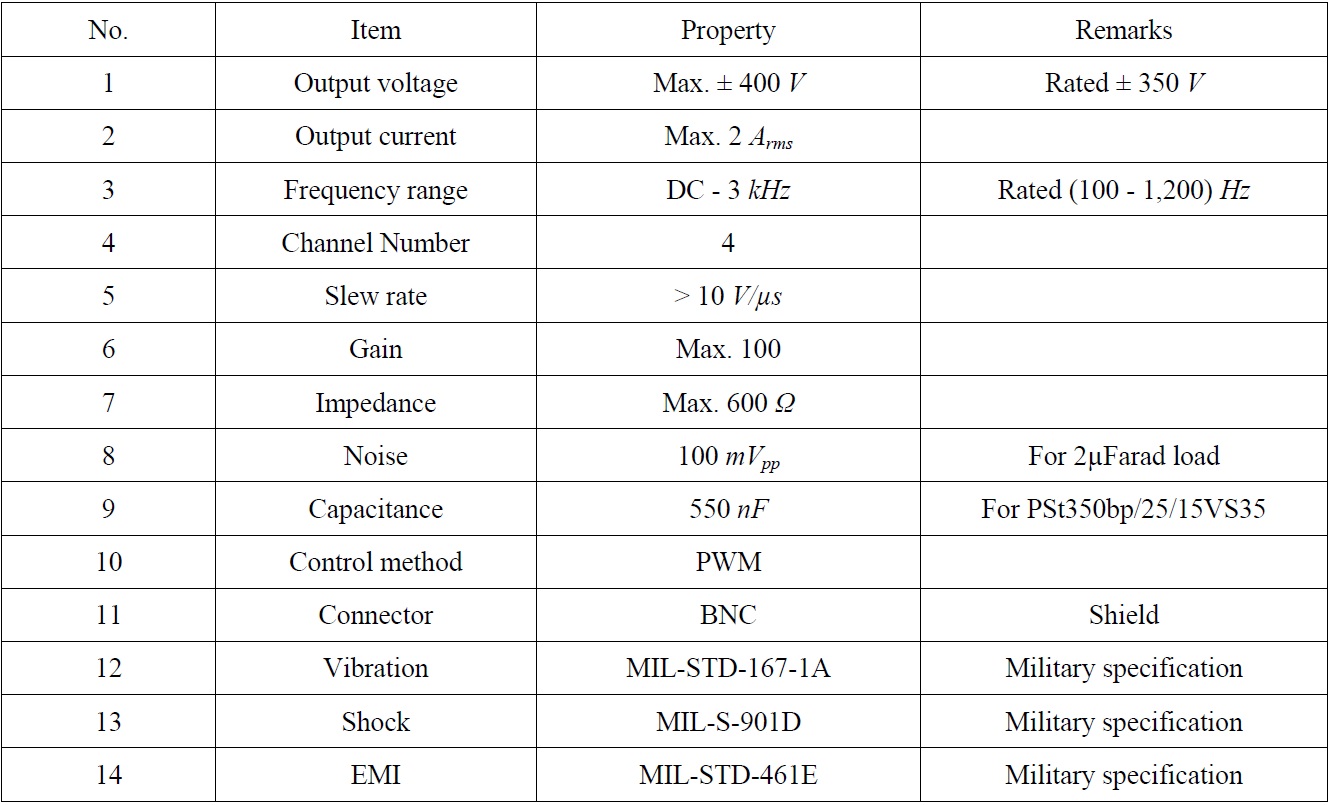
In order to evaluate the proposed hybrid mount system with the filtered-X LMS algorithm, the experimental apparatus was utilized as shown in Fig. 17. Because the voltage input into the piezostack actuator ranges from -350 V - +350 V, the voltage amplifiers should amplify the command voltages to the piezostack actuators. The voltage amplifiers should also be compatible with military specifications such as vibration (MIL-STD-167-1A (2005)), shock (MIL-S-901D (1989)), and electromagnetic interference (MIL-STD-461E (1999)). Since existing commercial voltage amplifiers could not meet the design requirements summarized in Table 3, a new voltage amplifier was developed. The voltage amplifier was designed to be lightweighted and compact in order to suppress vibration and shock loading. In addition, it was equipped with four wire-type isolators. In order to decrease the electromagnetic interference (EMI) from the voltage amplifier, several EMI shielding techniques were adopted using a strong grounding, an encapsulated cover box, an electrically conductive gasket, and a shield cable/connector, etc. According to MIL-STD-461E, EMI tests were successfully carried out.

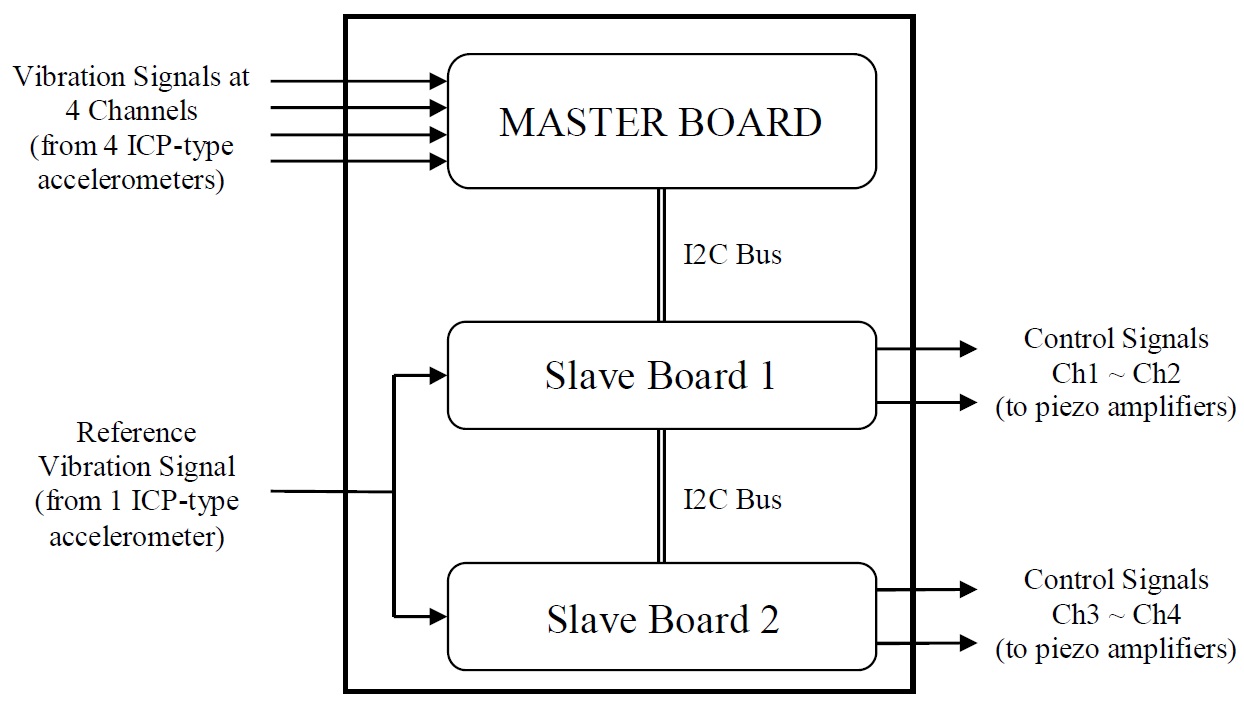
The command voltages to the voltage amplifiers were processed by a specific controller, which consists of a 5-channel analogue-digital (AD) converter, a 4-channel digital-analogue (DA) converter, and a microprocessor for digital signal processing. The AD converter can be connected directly with ICP-type sensors. Fig. 18 shows that the controller works on the basis of 3 dsPIC30F6014 microcontrollers (Microchip, Inc.) as the central processing unit, i.e., one master and two slaves. The voltage calculated in the controller was supplied to the piezostack actuators by the voltage amplifiers, and the measured acceleration signals were also digitalized by the controller. A total of five ICP-type sensitive accelerometers (B&K 752A13) were installed on the dummy weight and the bottom of each of the proposed hybrid mounts. In order to generate periodic external vibration at a specific frequency as unwanted vibration, the exciter (LDS V555), which can adjust the amplitude and frequency via a signal generator, Agilent 33210A, was installed on the top of the dummy weight.

Results

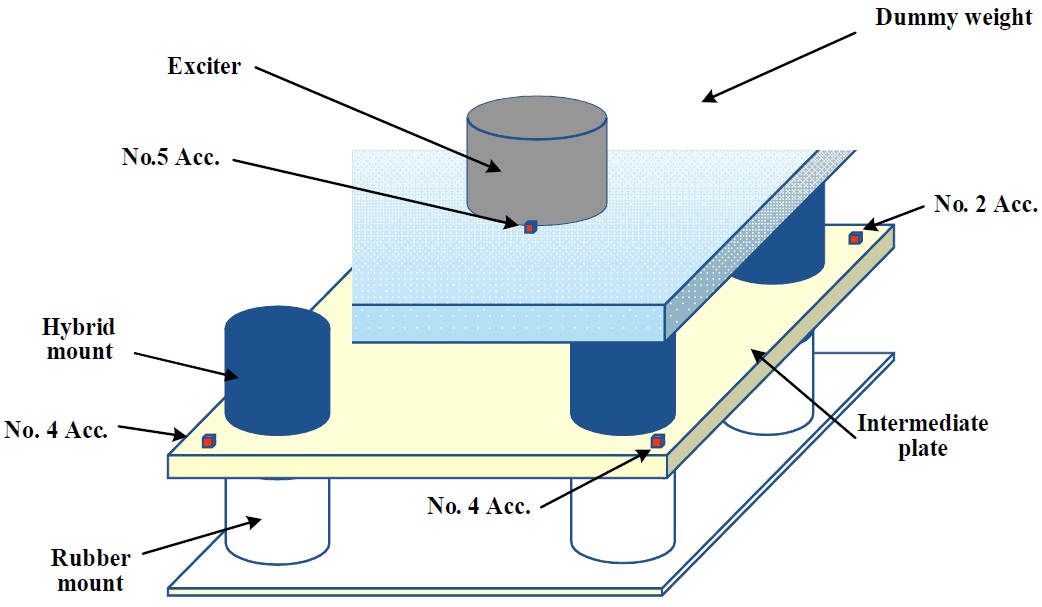
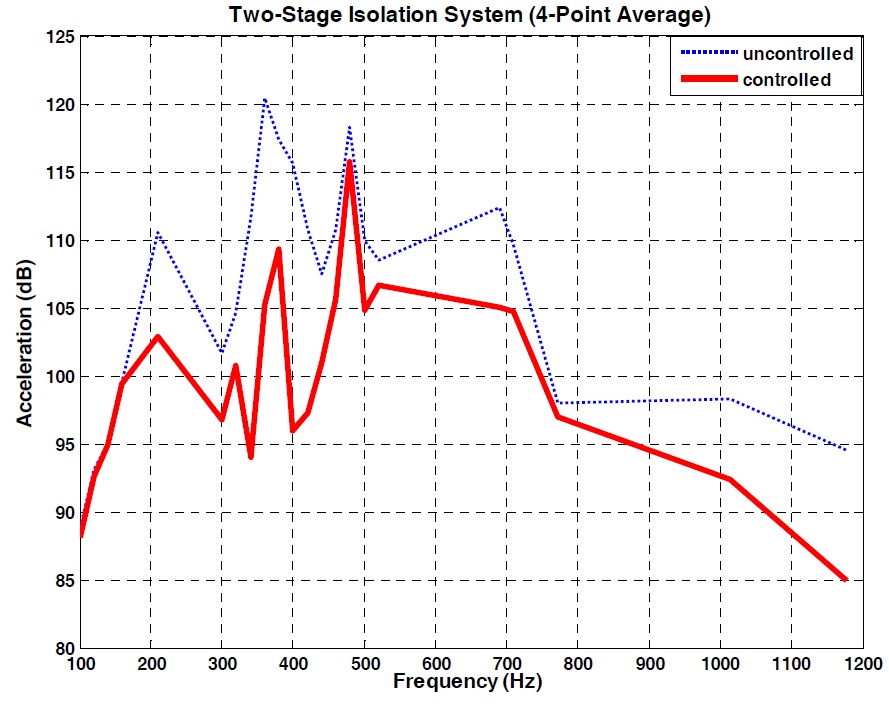
By vertically exciting the dummy weight with the exciter, the active performance test for the proposed hybrid system was carried out. Exciting force was applied to the dummy weight at constant amplitude and constant frequency. The exciting frequency was set up in the range of 100 Hz - 1,200 Hz with intervals of non-constant frequency. After passive performance was checked with the piezostack actuators switched off in the first stage, an active performance test was conducted with the piezostack actuators switched on. Acceleration transmissibility was calculated at each point of the hybrid mount based on measured acceleration at each point. Then, the average transmissibility was calculated. Fig. 19 shows the average acceleration transmissibility. Below 200 Hz, the active control performance is insignificant due to insufficient control force. From 200 Hz to 1,200 Hz, the differences between the two curves are approximately 2 dB - 11 dB. If picked up at the peaks, the differences can be plotted as shown in Fig. 20. In conclusion, the inertia-type of hybrid mount’s vibration suppression performance was actively enhanced by about 6.9 dB on average in the range of 100 Hz - 1,200 Hz compared to the passive type of mount.

An inertia-type hybrid mount comprising a rubber mount and a piezostack, with a maximum loading capacity of 500 kg, was developed for use with items of shipboard machinery in naval ships. The proposed hybrid mount combined a passive mounting device with active technology, which represents a new alternative for naval ships. While the passive rubber element is supporting static load, isolating unwanted vibration at high frequencies, and absorbing shock as a fail-safe device, the part composed of an active piezostack and an inertial mass enhances vibration suppression performance at high frequencies.

There are no specific military specifications regarding hybrid mounts for use on naval vessels. Because the hybrid mount was developed based on a resilient mount, both MIL-M-17185A(SHIPS) and MIL-M-17508F(SH) were optionally applied for the performance evaluation of the developed hybrid mount. The proposed hybrid mount was successfully passed on all of the testing items, including shock testing, according to MIL-S-901D. As regards active control performance, the hybrid mount can reduce vibration level by about 13 dB compared with the passive mount.

The hybrid mount system consists of the proposed hybrid mounts, a controller, and a voltage amplifier. The latter was specially designed according to MIL-STD-167-1A (vibration), MIL-S-901D (shock), and MIL-STD-462E (electromagnetic interference). A specific controller, consisting of an AD/DA converter and three microprocessors installed with the filtered-X LMS control algorithm, was also designed instead of a commercial control device. The active control performance test of the hybrid mount system was carried out on the two-stage isolating system. By conducting a series of experimental tests, it was confirmed that the hybrid mount system offers better performance than the passive 6K2000, which is the standard resilient mount of US Navy for use in naval ships.