Submarine pressure hulls consist of externally pressurized ring-stiffened cylindrical and conical shells and hemi-spherical or tori-spherical end closures. Due to the compressive stress state their design is governed by buckling where inelastic collapse occurs as one of several distinct modes or in some cases as a combination of them. Current design practice for these structures is based on a deterministic approach where each failure mode is artificially treated independent of each other. Failure criteria are determined either by prediction of collapse pressures for interframe collapse modes or setting a stress limit to avoid overall collapse mode for which generally accepted reliable strength modeling does not exist. Adequate safety factors are applied so that an unknown degree of conservatism is implicitly included and uncertainties caused by mode interactions, shape imperfecttions, residual stresses and modeling errors are covered. Design codes for pressure vessels such as PD 5500 (BSI, 2009), which was previously published as BS 5500, and the rules of Germanischer Lloyd (GL) (2009) for submarines and submersibles are examples of such a practice.
As semi-probabilistic methods using partial safety factors have been introduced over the last few decades for the design of offshore structures (Faulkner et al., 1983; Das et al., 1984; Das et al., 1992), several attempts have been also made to implement reliability analysis in submarine pressure hull design to overcome above mentioned uncertainties. Faulkner and Das (1991) performed a pilot study based on strength modeling given in BS 5500 and evaluated the suitability of reliability methods for submarine pressure hulls. Along with a later study (Faulkner, 1991), it was concluded that the failure associated with overall collapse is more likely than the interframe shell collapse modes due to large modeling uncertainties and conservative estimations. Results of one other study (based again on BS 5500), also supported this conclusion (Pegg, 1995), although from the design point of view, the pressure hull scantlings are selected such that interframe shell collapse precedes overall collapse as external pressure increases. In later studies, this result was explained in terms of the unrealistic models used in analysis and the deficiency in defining the modeling uncertainties by comparing obtained results with numerical predictions (Morandi et al., 1994; Morandi et al., 1996). Using the modeling factors quantified in the above mentioned studies, a reliability analysis was done by Das (1998) for a sample submarine pressure hull and showed that the probability of failure shows great sensitivity to modeling uncertainties rather than geometrical and material randomness. These studies clearly emphasized that there is an obvious need for improved strength modeling to use in reliability-based design approach for submarines.
Related to this issue, in a recent paper considering the inelastic overall collapse mode only, Radha and Rajagopalan (2006) performed a reliability analysis using Monte Carlo simulation with a proposed variance reduction technique where non-linear finite element analysis (NLFEA) results were used. Also, the uncertainty level in numerical evaluation of limit states of submarine pressure hulls has been assessed by the reviewing the literature (Mackay et al., 2011). NLFEA offers many advantages in that it takes material plasticity, non-linear geometrical effects and imperfections and realistic modeling of geometry into account. However, it is still too cumbersome to implement NLFEA in reliability analysis since there is no closed-form solution provided. Also, especially at the initial design stage, modeling of imperfections by assuming them in eigen-modes, that is in critical buckling modes or collapse-affine shapes in multi-wave continuous pattern with magnitude defined as in tolerance limits, may not likely to occur in practice and thus might be source of error.
Similar to the studies performed earlier for offshore structures (Das et al., 2003; Sun and Tan, 2006), the work presented in this paper concentrates on quantifying uncertainties arising from failure modeling of current design codes in terms of mean and coefficient of variation of bias by screening the available experimental data published for a further reliability study. A simple ultimate strength formulation for ring-stiffened cylinders taking into account the interaction between local and global failure modes and an ultimate strength formula for hemispherical shells which have better accuracy and reliability than current design codes is taken as basis for reliability analysis. Reference models representing realistic submarine pressure hull geometries are analyzed by means of Advanced First Order Reliability Method (AFORM). Failure probabilities are obtained as a function of external pressure. Important design variables are confirmed with sensitivity analysis confirms and comparisons are made with previous studies.
Prior to the reliability analysis, uncertainties involved in limit state of the structure concerned should be defined. These can be categorized into two groups, namely, physical uncertainties and model uncertainties. The first is due to the uncertainties in physical quantities such as material properties and dimensions while latter is used define the uncertainties of mathematical models and methods used in evaluating response of structure under certain loads as result of assumption, simplifications and uncertain boundary conditions. Two parameters are considered for quantifying the modeling uncertainties. The mean of modeling uncertainty factor
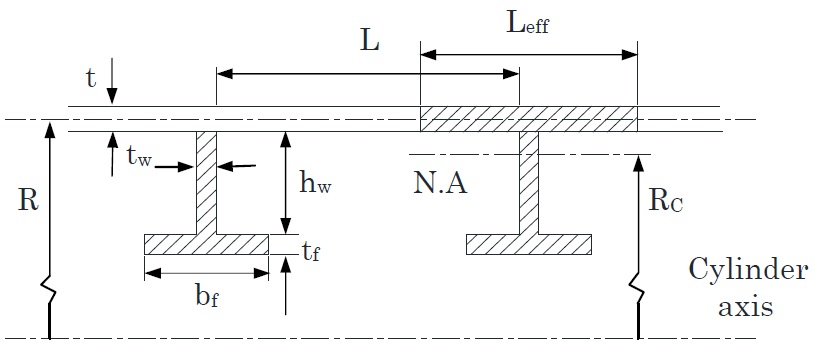
Failure of ring-stiffened cylinders under external hydrostatic pressure can be precipitated by any or a combination of three basic modes. These three modes can also be classified into two main groups. The first two modes are interframe shell collapse modes where the collapse occurs between adjacent stiffeners. Buckling can be either axisymmetric or asymmetric. For axisymmetric buckling the collapse mode is characterized by an accordion-type pleat, which may or may not extend around the periphery. In asymmetric buckling the failure mode is characterized by inward-outward lobes that may or may not develop around the entire periphery. In reality, since the shell is stressed beyond the proportionality limit of the material, buckling occurs inelastically. Failure in each mode is dependent on the shell thickness radius ratio, stiffener-spacing radius ratio, stiffener crosssectional area to shell cross-sectional area, and the stress-strain relationship of the materials involved. As a rule of thumb a pressure hull is more prone to fail asymmetrically if the stiffeners are widely spaced and the cylinder shell is relatively thin. In Fig. 1, typical cases for these failure modes are given.
The shell can also buckle with attached stiffeners which may extend over the entire length of the cylinder where the cylinder boundaries (usually rigid bulkheads or dome ends) provide some level of fixity. This is called collapse by general instability or overall collapse. This mode is triggered by the presence of weak stiffeners, out-of circularities in shell and the ratio of cylinder radius to cylinder overall length. In Fig. 2, a model failed by means of overall collapse is shown.
In addition to these three global collapse modes there are local modes such as frame tripping and frame yielding which usually set off and accompany overall collapse. In this study these local modes are avoided.
The end closures of pressure hulls are usually hemispheres or tori-spheres which are unstiffened and collapse in overall manner. Fabrication caused imperfections, residual stresses and unevenness of thickness precipitates the collapse of these structures. In Fig. 3, a collapsed hemisphere model is shown.
Ring-stiffened cylinders
As stated by Das (1998) the interaction between interframe and overall collapse can be up to a considerable degree in real practice. In order to overcome this deficiency in present design thinking, in this study following ultimate strength formulation based on generalized Merchant-Rankine formula is put forward (Cho et al., 2004):
where
Interframe elastic buckling pressure is to be calculated by the equation given by von Mises (1929) as follows:
where
Overall elastic buckling pressure is obtained by the formula given by Bryant (1954), expressed as:
where
The pressure to cause yield in midbay between stiffeners is calculated according to Wilson (1966) as follows:
where
In above equations
For evaluation of the knockdown factors the existing test data (Kendrick, 1955; Miller and Kinra, 1981) of fabricated steel ring-stiffened cylinders were considered together with additional six experiments performed earlier. Due to method of fabrication, these test models have considerable residual stresses and imperfections similar to the real practice and they generally fail in the elasto-plastic regime. Accordingly, following expressions are derived to calculate the knockdown factors:
In the design guidelines given by Germanischer Lloyd (2009) the basis is the theoretical and experimental work done in the David Taylor Model Basin (DTMB) which has been partly released to public. For interframe shell collapse modes, Lunchick and Reynolds from DTMB presented solutions for inelastic axisymmetric and asymmetric buckling modes, respectively, based on the differential equations of equilibrium for plastic range of cylindrical shells (Pulos, 1963). In their solutions the buckling pressures are a function of the cylinder geometry and the tangent modulus
Hemispherical dome ends
The ultimate strength of externally pressurized hemispherical shells can be predicted by considering quadratic interaction between the elastic buckling and yield pressure using a formulation (Cho et al., 2011) based on Merchant-Rankine formula as follows:
where
where
>
Quantifying modeling uncertainties
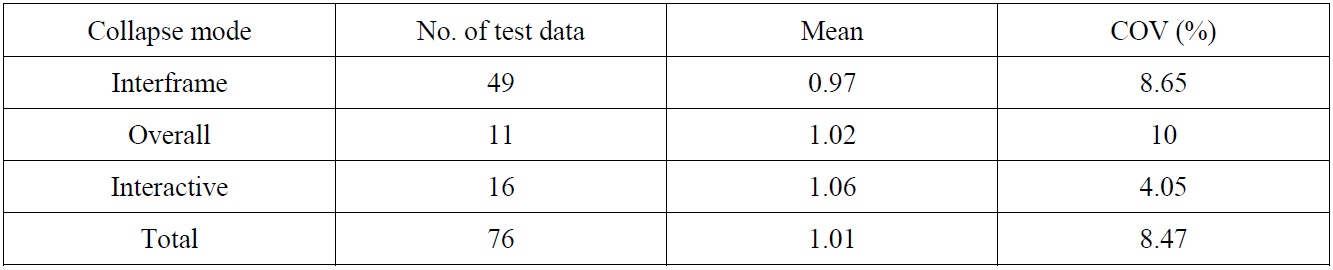
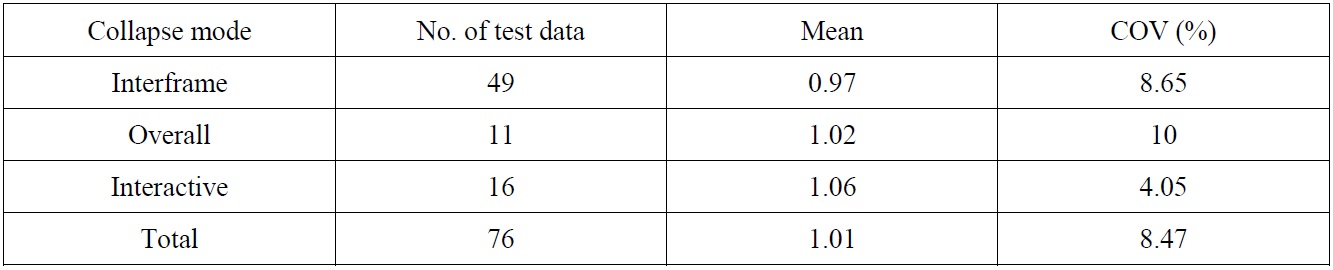
In order to define the modeling uncertainties of ultimate strength formulation for the externally pressurized ring-stiffened cylinders, the experimental test data which consists of 76 models mentioned earlier for the knockdown factor evaluation is utilized. This experimental data includes the models where the collapse mode can be identified as either interframe collapse, overall collapse or interactive collapse. The range of geometric and material parameters of utilized experimental data is given in Table 1.

Range of geometric and material parameters of experimental data for ring-stiffened cylinders.
Modeling properties for externally pressurized ring-stiffened cylinder ultimate strength prediction method.
In Table 2, the modeling properties for above given prediction method are summarized. From the given data, it is evident that the statistical properties of the given ultimate strength prediction method are quite good and are thus reliable. The COV value is within the acceptable limits as defined by Faulkner et al. (1987) for any good strength prediction tool for marine structures (< 13%) and the bias is also close to unity.
On the other hand PD 5500 requires calculation of the elastic buckling pressure and yield pressure and the use of mean or lower bound design curves approximately fitted to experimental data for empirically predicting the interframe shell collapse pressure. The biases and COVs are dependent on the ratio of elastic buckling pressure pm, to pressure causing circumferential stress to reach yield stress in the cylinder shell
[Table 3] Modeling properties for the PD 5500 mean strength curve for interframe shell collapse.

Modeling properties for the PD 5500 mean strength curve for interframe shell collapse.
For overall collapse, considering the bending stresses caused by a predefined 0.5% out-of-circularity of the cylinder radius and the worst possible elastic overall buckling mode, the stress in the stiffener flange should be kept smaller than the yield stress. For this criterion, there is no assessment made totally based on experimental data (Das, 1998). Rather, in reliability analysis, parameters determined with a pessimistic judgment are used, for instance Faulkner (1991) assumes mean of
For collapse prediction methods developed in DTMB, which form the basis of Germanischer Lloyd design guidelines, using the above mentioned experimental data the modeling properties are assessed. Since there is no distinction made for interframe collapse modes in experimental data, the models which failed by interframe collapse mode were utilized both for axisymmetric and asymmetric buckling collapse prediction methods. Also, the models failed by interactive collapse were considered for all prediction methods. The results are given in Table 4.
[Table 4] Modeling properties for the collapse prediction methods developed in DTMB.

Modeling properties for the collapse prediction methods developed in DTMB.
Although for all the modes, collapse prediction methods scattering in prediction is quite low, the mean values are lower than unity, which indicates an overprediction in collapse pressures. This is especially valid for axisymmetric buckling where usually asymmetric buckling precedes in models failing by interframe collapse. For overall collapse prediction method, the sensitivity of accuracy on out-of-circularity (OOC) is to be mentioned. In this study, only the models with reasonably small OOC were considered.
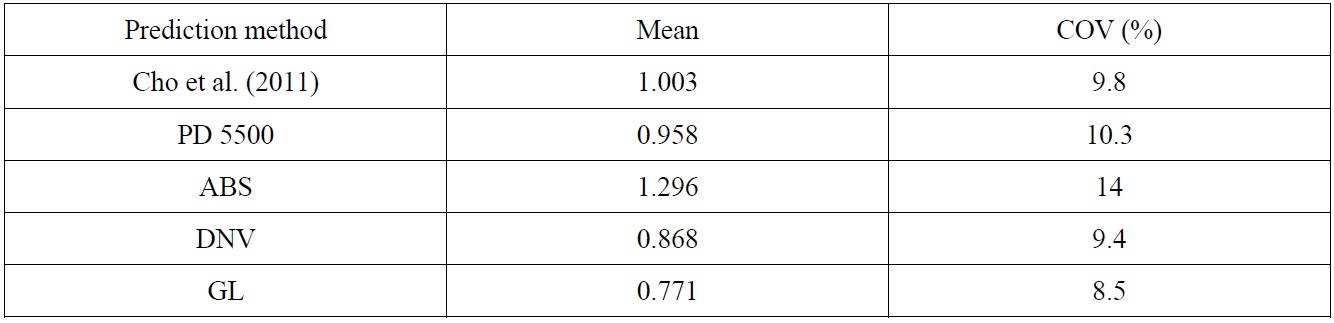
For the ultimate strength formulation of hemispheres, Cho et al. (2011) presented the modeling properties along with the ones for several design codes including PD5500 (BSI, 2009), ABS (2002), DNV (1992) and GL (2009) using test results of welded hemispheres. The collected data consists of 29 models having
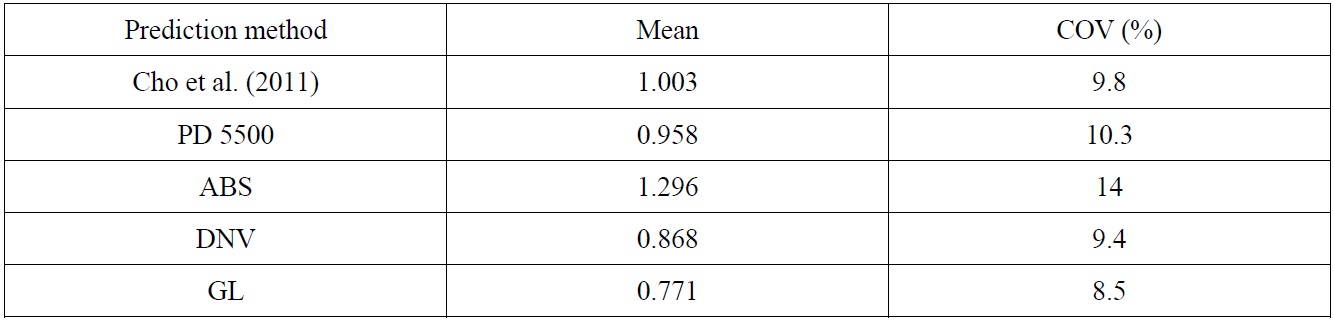
Modeling properties for the collapse prediction methods of externally pressurized hemi-spheres.
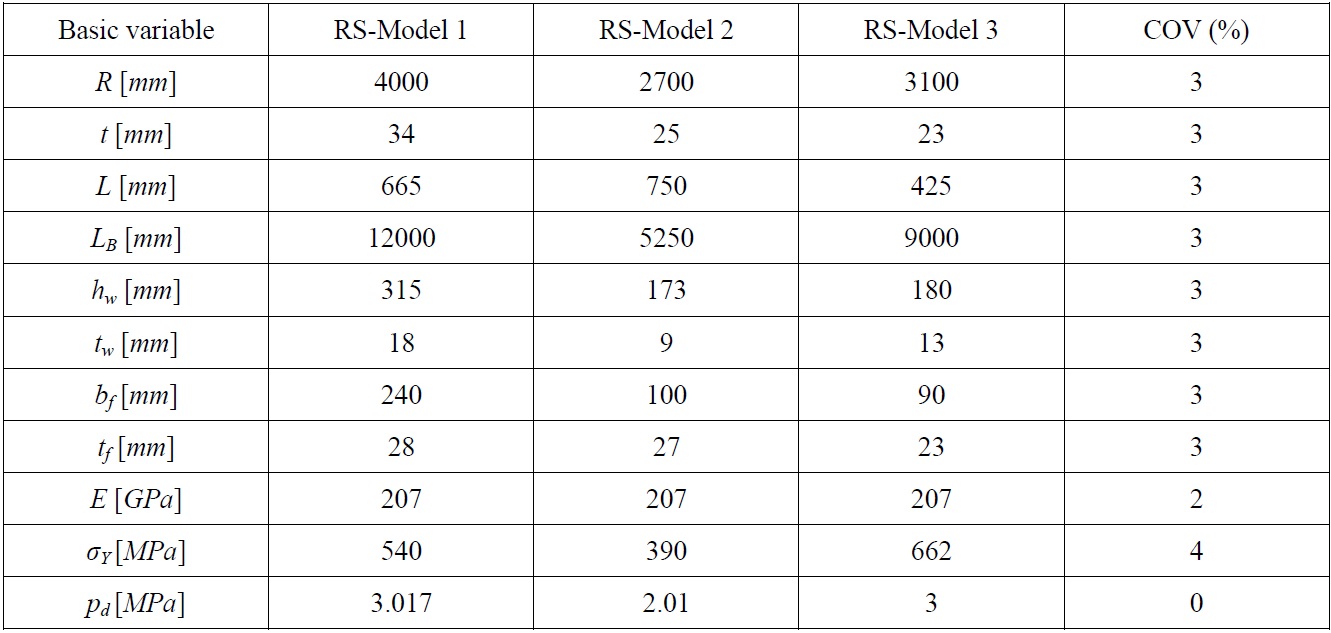
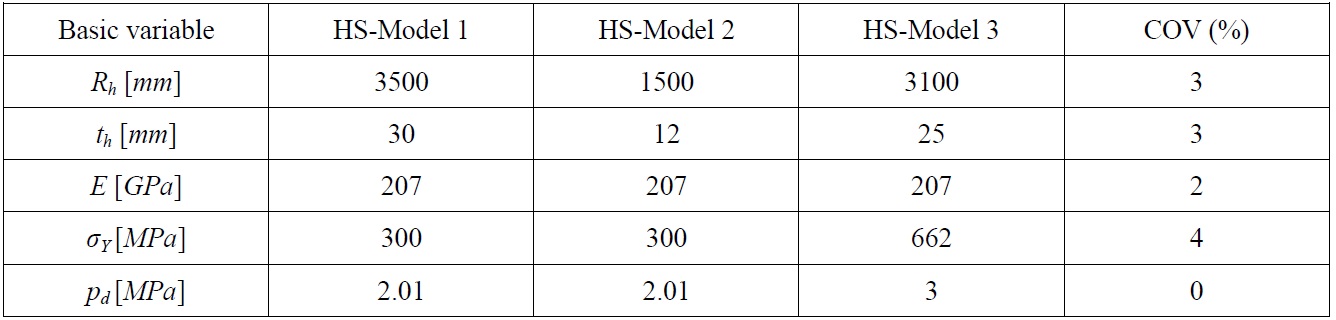
Once establishing the modeling properties, a reliability analysis is performed for reference submarine pressure hull models. In addition to the modeling uncertainties, the randomness in geometric and material properties is considered. As ring-stiffened cylinder three reference models are considered, where RS-Model 1 is having the same properties as the model used by Das (1998) and RS-Model 2 is as used by Faulkner (1991) in his studies. These two models were proportioned according to PD 5500. RS-Model 3 is added to those two models which thought to represent more realistic scantlings of submarine pressure hulls. Also for RS-Model 3, assumed hull material is HY-80 steel for which rather than nominal value, mean value of yield stress is assumed.
The reliability analyses are performed using in-house computer code implementing Advanced First Order Reliability Method (AFORM) which is based on the Hasofer-Lind method (Hasofer and Lind, 1974) extended to include non-normally distributed variables. The safety margin is defined as
where
where
where
The reliability index
From the equation (23) the sensitivity factor α for each random variable is defined as follows
The Hasofer-Lind reliability index is geometrically the shortest distance to the failure surface from the origin in reduced variable space. The coordinates of the design point can be obtained from the following relationship:
As mentioned earlier, the design points should satisfy
Once the reliability index is obtained, the probability of failure is then given by
where Φ is standardized normal distribution function.
where
Non-normally distributed variables are transformed using two parameter normal tail approximation (Rackwitz and Fiessler, 1977) in which the values of cumulative distribution function
From these two equations equivalent mean
In Table 6, for each model, the statistical properties of basic variables assumed in reliability analysis are given. Except yield stress, which has a log-normal distribution, all variables, including modeling parameter
[Table 6] Statistical properties of basic variables for ring-stiffened cylinder models.
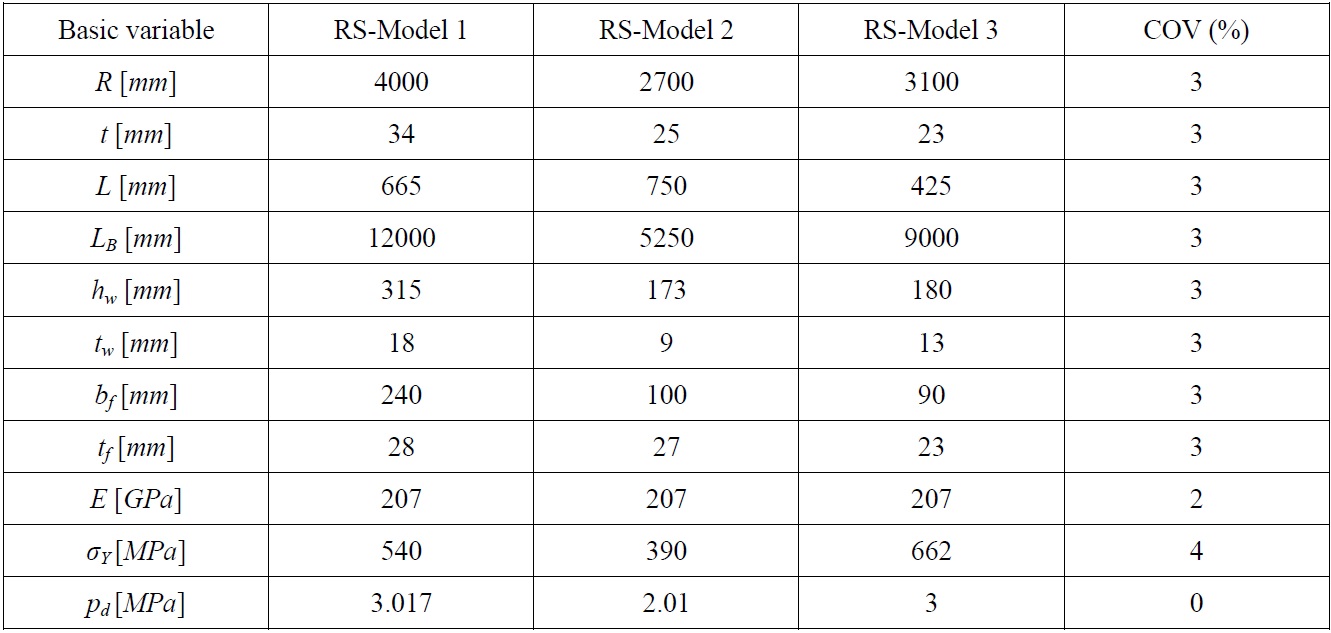
Statistical properties of basic variables for ring-stiffened cylinder models.
As hemisphere reference models three models are utilized. In Table 7 the properties of each model are given.
[Table 7] Statistical properties of basic variables for hemi-sphere models.
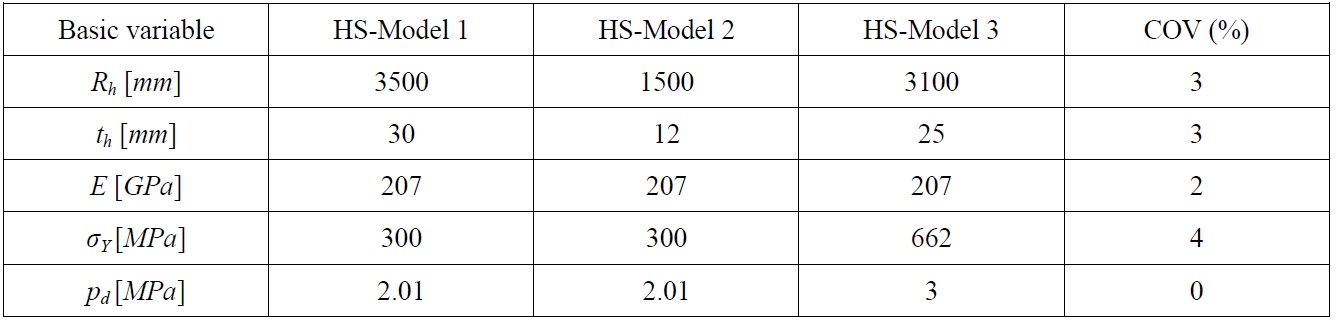
Statistical properties of basic variables for hemi-sphere models.
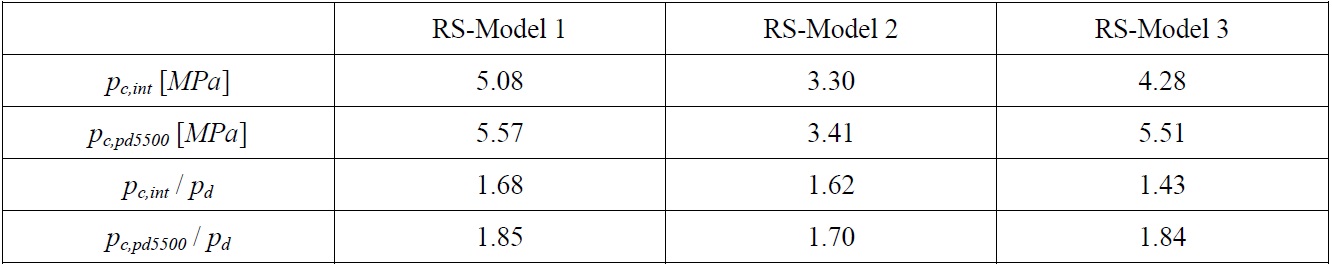
Collapse pressures obtained with deterministic approach for ring-stiffened cylinder models.
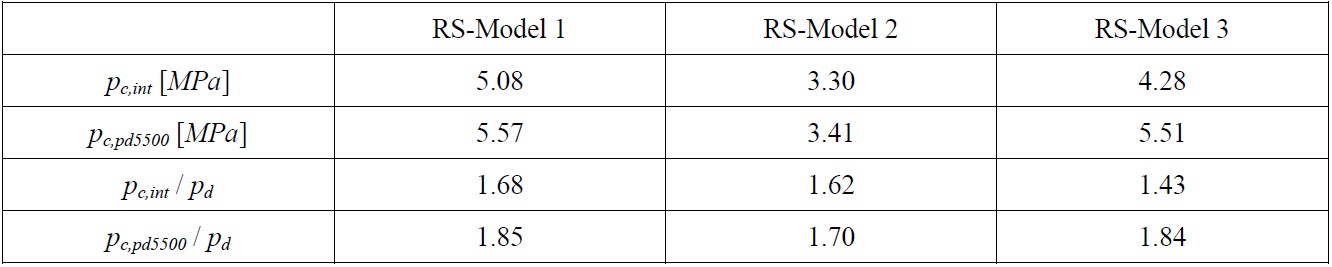
Before proceeding to reliability analysis, using the mean values of each variable, the collapse pressures were calculated both with previously explained method (designated as
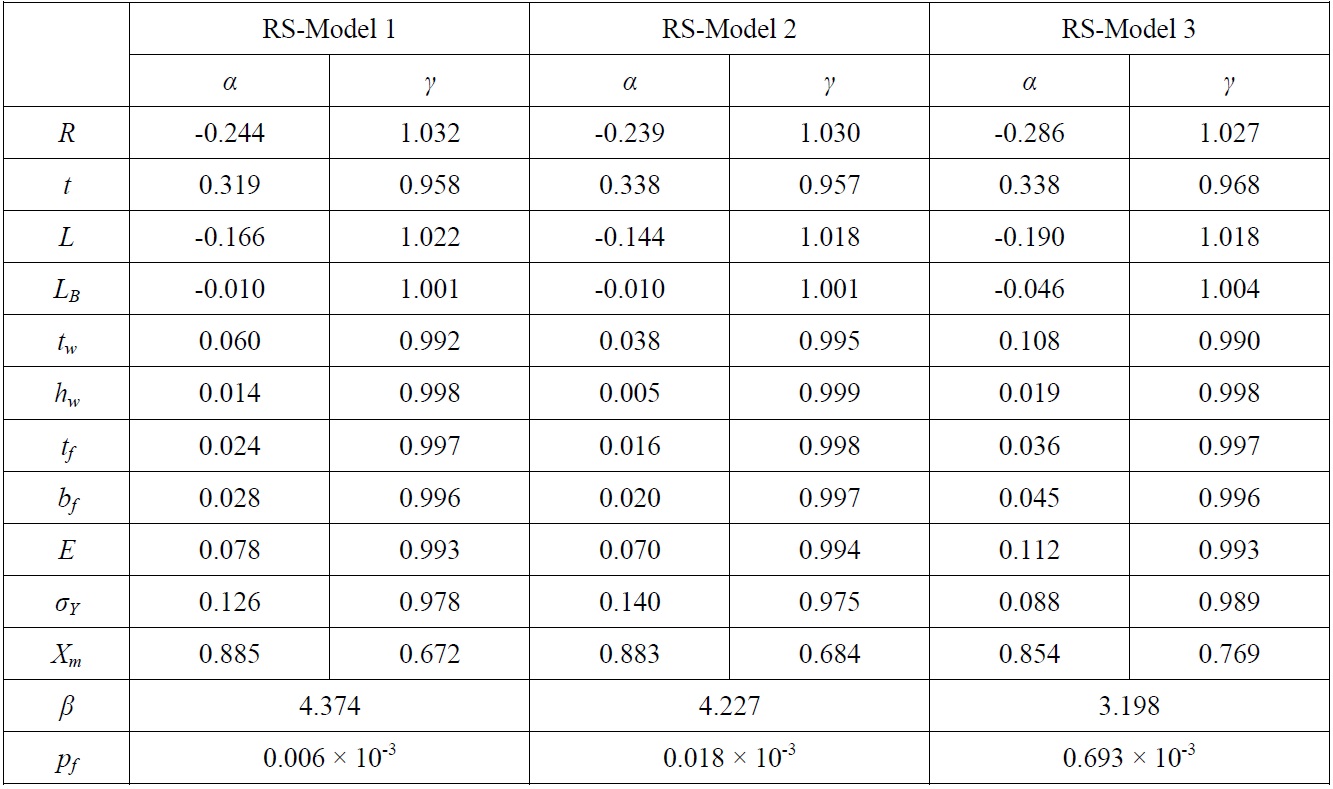
One conclusion can be drawn from the above results is that although the models were proportioned according to PD 5500 which have safety factor of 1.75 against interframe collapse, for the ultimate strength formula given; the value of the safety factor is lower. For the Model 3 the difference is more significant. This result suggests that considering any interaction between collapse modes gives obviously lower collapse pressures. The results obtained through the reliability analysis using the given ultimate strength prediction method are shown in Table 9 for each model.
[Table 9] Results of reliability analysis for each ring-stiffened cylinder model.
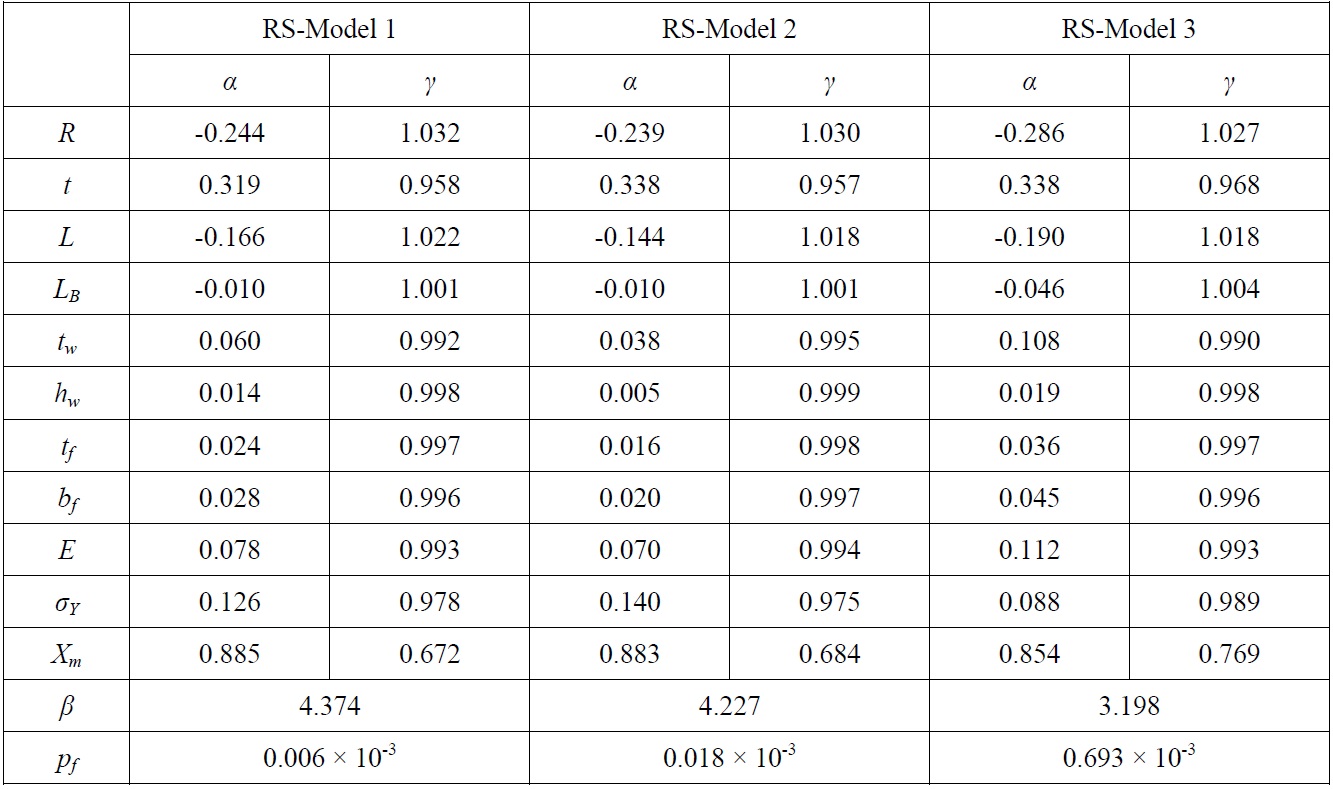
Results of reliability analysis for each ring-stiffened cylinder model.
As it is apparent, the sensitivity factors do not differ much for all models. Also, the modeling parameter
Considering the partial safety factors, except modeling parameter, it can be inferred that they are close to unity. This suggests that for codifying given ultimate strength prediction method, for a given target reliability index in the range of those obtained for three models, a partial safety factor for modeling covering also design and fabrication uncertainties would be dominated by the uncertainty in strength modeling. It is believed that such safety factor would be much suitable than a fixed value one applied to an empirically obtained collapse pressure without considering any uncertainty in strength prediction. However, it requires evaluating a set of various and realistic models and it is beyond the scope of this study.
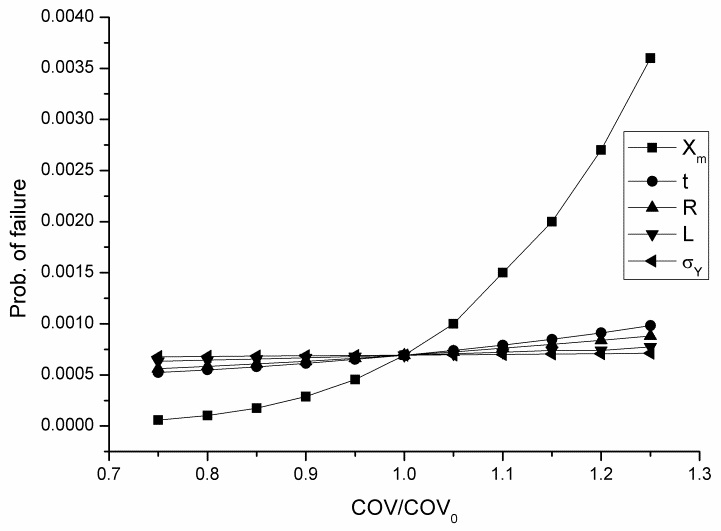
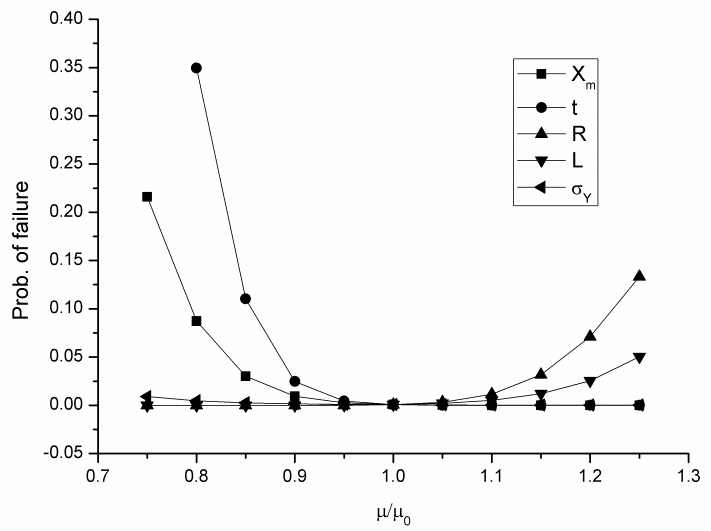
Once the important variables affecting the failure probability is determined the effects of minor changes in these variables are assessed. For changes in standard deviation and mean variation in probability of failure for RS-Model 3 is shown in Fig. 5 and Fig. 6, respectively.
From these figures the sensitivity to variation in bias is confirmed. On the other hand, from Fig. 6, for the case of minor decrease in thickness seem to influence the failure probability significantly. If relative contribution of each variable to failure probability is taking into fact, this result may give an idea for selecting design values for each variable.
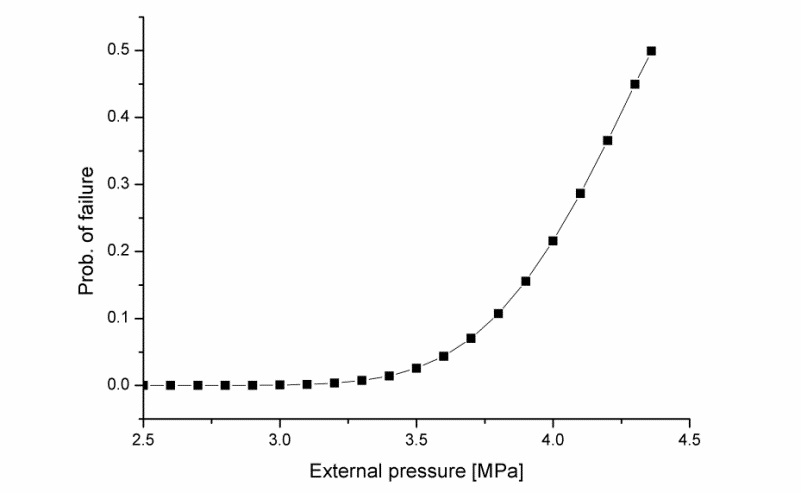
Another aspect of probabilistic approach to structural design of submarines is risk assessment for diving depth change. This can be achieved simply evaluating probability of failure and corresponding reliability index with consecutive reliability analyses with increasing deterministic external pressure. For RS-Model 3 the results are shown in Fig. 7.
The risk of any increase in external pressure which might be caused by depth excursion intentionally or accidentally can be assessed easily from the graph. Since one single collapse pressure is obtained from the given ultimate strength prediction method by considering any interaction between interframe and overall collapse modes, the total failure probability is not a sum of individual failure probabilities for each collapse mode as it was treated in previous studies. However, if the same procedure would be applied, the tendency of structure to collapse in a specific mode can be also determined. It might be useful to obtain a design with balanced collapse tendencies rather than avoidance of overall collapse modes by setting criteria based on conservative assumptions.
Beside the design diving depth, as given in the rules of Germanischer Lloyd (2009), a test diving depth and a correspondding external pressure is usually considered which is not to be reached frequently during service. Accordingly, for a lower target reliability index, partial safety factors can be derived for test diving depth.
The reliability analysis is also performed for hem-spherical models. The results are given in Table 10.
[Table 10] Results of reliability analysis for each hemi-sphere model.

Results of reliability analysis for each hemi-sphere model.
As in the case of ring-stiffened cylinders, the sensitivity factor of the modeling uncertainty is larger than the sensitivity factors of geometric and material properties. Thus, in a design code for externally pressurized hemi-spheres partial safety factors to be derived will be dominated by uncertainty in modeling. For system reliability analysis considering two components, namely, ring-stiffened cylinders and hemi-spherical dome ends, total probability of failure can be assessed as the sum of the probability of failure of each component, though failure of these two components is not independent from each other in real case.
In this paper modeling uncertainties for reliability analysis of submarine pressure hull structures were addressed and following conclusions were drawn:
According modeling uncertainty assessment, for PD 5500, scattering in strength prediction and uncertainty in modeling of strength against overall collapse is noticed. For design guidelines of Germanischer Lloyd slight overprediction is observed.
An ultimate strength formulation proposed considering interaction between interframe and overall collapse mode and calibrated using available test data is shown to be more robust than current design codes.
From the results of reliability analysis it is concluded that the modeling uncertainty factor still has significance as showed in the sensitivity analysis. It can be stated that in probabilistic submarine pressure hull design, the strength distribution is governed by deviation in collapse prediction. This conclusion is also supported by the fact that the production and main overhaul inspections do not allow any significant deviations from the values set by tolerance limits for geometry and materials.
Also, it is shown that the thickness of cylinder shell, cylinder radius and stiffener spacing is influential on collapse. It is also shown that the risks associated with overdiving or at-test diving can be determined via reliability analysis rather than setting a certain maximum diving depth. It is believed that the goal of applying safety factors in current design practice such as 1.75 for interframe shell collapse in PD 5500, is to allow a safe region for such overdiving.
The reliability analysis of hemi-spherical models also showed that the probability of failure is mainly governed by deviations in strength modeling.
While the reliability theory is successfully applied to several representative models as a preliminary study, in future, with the conclusions of this study, defining target reliability levels for both design depth and test depth, establishing a design code format and evaluation of partial safety factors by considering a range of realistic geometries and statistical properties keeping the tolerance limits during fabrication and service are tasks to be attempted. So called statistical uncertainty has to be also dealt with by defining the scattering in variables and distributions more accurately, rather than assumptions as in this study. On the other hand, the findings in this paper can also serve to indicate any deficiency or redundancy in the scope of tolerances.